- 6 многогранник
 6-симплекс |
В шестимерной геометрии существует 35 однородных многогранников с A6 симметрией . Существует одна самодвойственная правильная форма — 6-симплекс с 7 вершинами.
Каждую из них можно представить как симметричные ортогональные проекции в плоскостях Кокстера группы А 6 Кокстера и других подгрупп.
Графики
[ редактировать ]Симметричные ортогональные проекции этих 35 многогранников можно построить в A6 , A5 , A4 , A3 , A2 плоскостях Кокстера . A k Графы имеют симметрию [k+1] . Для четных k и симметричных кольцевых диаграмм симметрия удваивается до [2(k+1)] .
Каждый из этих 35 многогранников показан в этих 5 плоскостях симметрии, с нарисованными вершинами и ребрами, а вершины окрашены в соответствии с количеством перекрывающихся вершин в каждой проективной позиции.
| # | А 6 [7] | AА5 [6] | A 4 [5] | AА3 [4] | AА2 [3] | Диаграмма Кокстера-Динкина Символ Шлефли Имя |
|---|---|---|---|---|---|---|
| 1 |  |  |  |  |  | т 0 {3,3,3,3,3} 6-симплекс Гептапетон (хмель) |
| 2 |  | 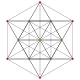 |  |  |  | т 1 {3,3,3,3,3} Выпрямленный 6-симплекс Ректифицированный гептапетон (рил) |
| 3 |  |  |  |  | 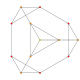 | т 0,1 {3.3.3.3.3} Усеченный 6-симплекс Усеченный гептапетон (тиль) |
| 4 |  |  |  |  |  | т 2 {3,3,3,3,3} Биректифицированный 6-симплекс Биректифицированный гептапетон (бриль) |
| 5 |  |  |  |  |  | т 0,2 {3.3.3.3.3} Сочлененный 6-симплекс Малый ромбированный гептапетон (шрил) |
| 6 |  |  |  |  | 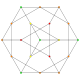 | т 1,2 {3,3,3,3,3} Битусеченный 6-симплекс Усеченный гептапетон (батальный) |
| 7 |  |  |  | 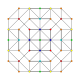 |  | т 0,1,2 {3,3,3,3,3} Количественно усеченный 6-симплекс Большой ромбовидный гептапетон (гриль) |
| 8 |  |  |  |  |  | т 0,3 {3.3.3.3.3} Ранцинированный 6-симплекс Малый призматический гептапетон (дичь) |
| 9 |  | 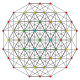 |  |  |  | т 1,3 {3,3,3,3,3} Двукантеллированный 6-симплекс Малый бирромбовидный гептапетон (сабрил) |
| 10 |  | 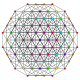 |  |  |  | т 0,1,3 {3,3,3,3,3} Runcitусеченный 6-симплекс Призматоусеченный гептапетон (патал) |
| 11 |  |  |  |  |  | т 2,3 {3,3,3,3,3} Трехусеченный 6-симплекс Тетрадекапетон (fe) |
| 12 |  |  |  | 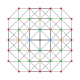 |  | т 0,2,3 {3,3,3,3,3} Рунцикантеллярный 6-симплекс Призматоромбатированный гептапетон (прил) |
| 13 |  |  | 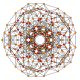 |  | 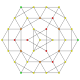 | т 1,2,3 {3,3,3,3,3} Бикантиусеченный 6-симплекс Большой бирромбовидный гептапетон (габриль) |
| 14 |  | 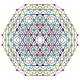 |  |  | 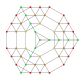 | т 0,1,2,3 {3,3,3,3,3} Ранчикантиусеченный 6-симплекс Большой призматичный гептапетон (гапил) |
| 15 |  |  |  |  |  | т 0,4 {3.3.3.3.3} Стерический 6-симплекс Мелкоклеточный гептапетон (чешуйка) |
| 16 |  | 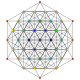 | 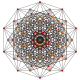 |  |  | т 1,4 {3,3,3,3,3} Бирунцированный 6-симплекс Малый бипризмато-тетрадекапетон (сибпоф) |
| 17 |  |  |  |  | 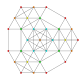 | т 0,1,4 {3,3,3,3,3} Стеритусеченный 6-симплекс целлиусеченный гептапетон (катал) |
| 18 |  |  |  | 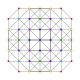 |  | т 0,2,4 {3,3,3,3,3} Стериконтеллярный 6-симплекс Целлиромбовидный гептапетон (краль) |
| 19 |  |  |  |  | 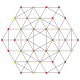 | т 1,2,4 {3,3,3,3,3} Бирюроусеченный 6-симплекс Бипризматоромбатированный гептапетон (баприл) |
| 20 |  |  |  |  | 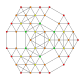 | т 0,1,2,4 {3,3,3,3,3} Стерикантиусеченный 6-симплекс Целлигреаторромбовидный гептапетон (каграл) |
| 21 |  |  |  |  |  | т 0,3,4 {3,3,3,3,3} Стерильный 6-симплекс Целлипризматический гептапетон (копал) |
| 22 |  |  | 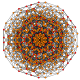 |  |  | т 0,1,3,4 {3,3,3,3,3} Стерирунный усеченный 6-симплекс целлипризматоусеченный гептапетон (каптал) |
| 23 |  |  | 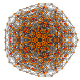 |  | 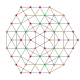 | т 0,2,3,4 {3,3,3,3,3} Стерирунцикантеллярный 6-симплекс целлипризматор ромбовидный гептапетон (коприл) |
| 24 |  |  |  |  |  | т 1,2,3,4 {3,3,3,3,3} Бирунцикантиусеченный 6-симплекс Большой бипризмато-тетрадекапетон (гибпоф) |
| 25 |  | 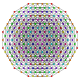 |  |  | 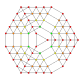 | т 0,1,2,3,4 {3,3,3,3,3} Стерирунцикантиусеченный 6-симплекс Большой клеточный гептапетон (гакал) |
| 26 |  |  |  |  | 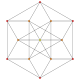 | т 0,5 {3,3,3,3,3} Пятеричный 6-симплекс Малый тери-тетрадекапетон (стаф) |
| 27 |  |  | 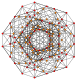 | 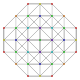 | 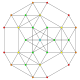 | т 0,1,5 {3,3,3,3,3} Пятиусеченный 6-симплекс Терицеллярный гептапетон (токальный) |
| 28 |  |  |  |  |  | т 0,2,5 {3,3,3,3,3} Пятиконтеллярный 6-симплекс Терипризматический гептапетон (тапал) |
| 29 |  |  |  |  |  | т 0,1,2,5 {3,3,3,3,3} Пентикантиусеченный 6-симплекс Теригреаторромбовидный гептапетон (тограл) |
| 30 |  | 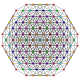 | 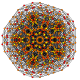 |  | 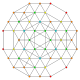 | т 0,1,3,5 {3,3,3,3,3} Пятиусеченный 6-симплекс Терицеллиромбовидный гептапетон (токрал) |
| 31 |  |  |  |  |  | т 0,2,3,5 {3,3,3,3,3} Пятирунцикантеллярный 6-симплекс Терипризматоромби-тетрадекапетон (тапорф) |
| 32 |  |  |  |  | 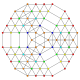 | т 0,1,2,3,5 {3,3,3,3,3} Пятигранникантитусеченный 6-симплекс Теригреатопризматический гептапетон (тагопал) |
| 33 |  |  |  |  |  | т 0,1,4,5 {3,3,3,3,3} Пентистеритусеченный 6-симплекс терицеллитрунки-тетрадекапетон (тактаф) |
| 34 |  |  |  |  | 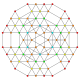 | т 0,1,2,4,5 {3,3,3,3,3} Пентистерикантиусеченный 6-симплекс терицеллигреатор ромбовидный гептапетон (такограл) |
| 35 |  |  |  |  |  | т 0,1,2,3,4,5 {3,3,3,3,3} Всеусеченный 6-симплекс Большой тери-тетрадекапетон (готаф) |
Ссылки
[ редактировать ]- ХСМ Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
Внешние ссылки
[ редактировать ]- Клитцинг, Ричард. «6D однородные многогранники (полипеты)» .