Мириагон
| Обычный многоугольник | |
|---|---|
 Обычный мириагон | |
| Тип | Правильный многоугольник |
| Ребра и вершины | 10000 |
| Символ Шлефли | {10000}, т{5000}, тт{2500}, ттт{1250}, тттт{625} |
| Диаграммы Кокстера – Динкина | |
| Группа симметрии | Двугранник (Д 10000 ), заказ 2х10000 |
| Внутренний угол ( градусы ) | 179.964° |
| Характеристики | Выпуклый , циклический , равносторонний , изогональный , изотоксальный |
| Двойной полигон | Себя |
В геометрии мириагон или 10 000 -угольник — это многоугольник с 10 000 сторон. Некоторые философы использовали правильный мириагон для иллюстрации вопросов, касающихся мышления. [1] [2] [3] [4] [5]
Обычный многоугольник
[ редактировать ]Правильный , многоугольник представлен символом Шлефли {10 000} и может быть построен в виде усеченного 5000-угольника, t{5000}, дважды усеченного 2500-угольника, tt{2500}, или трижды усеченного 1250-угольника ttt{1250}, или усечённый в четыре раза 625-угольник, tttt{625}.
Размер каждого внутреннего угла правильного многоугольника равен 179,964°. Площадь a правильного многоугольника сторонами длины со определяется выражением
Результат отличается от площади описанной окружности до 40 частей на миллиард .
Потому что 10 000 = 2 4 × 5 4 , число сторон не является ни произведением различных простых чисел Ферма , ни степенью двойки. Таким образом, правильный многоугольник не является конструктивным многоугольником . В самом деле, его невозможно построить даже с использованием трисектора угла, поскольку число сторон не является ни произведением различных простых чисел Пьерпона , ни произведением степеней двойки и трех.
Симметрия
[ редактировать ]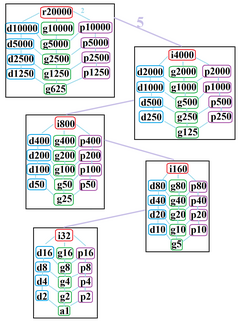
Правильный многоугольник имеет Dih 10 000 двугранную симметрию порядка 20 000, представленную 10 000 линиями отражения. Дих 10000 имеет 24 двугранных подгруппы: (Дих 5000 , Дих 2500 , Дих 1250 , Дих 625 ), (Дих 2000 , Дих 1000 , Дих 500 , Дих 250 , Дих 125 ), (Дих 400 , Дих 200 , Дих 100 ). , Дих 50 , Дих 25 ), (Дих 80 , Дих 40 , Дих 20 , Дих 10 , Дих 5 ) и (Дих 16 , Дих 8 , Дих 4 , Дих 2 , Дих 1 ). Он также имеет еще 25 циклических симметрий в виде подгрупп: (Z 10000 , Z 5000 , Z 2500 , Z 1250 , Z 625 ), (Z 2000 , Z 1000 , Z 500 , Z 250 , Z 125 ), (Z 400 , Z 200) . , Z 100 , Z 50 , Z 25 ), (Z 80 , Z 40 , Z 20 , Z 10 ) и (Z 16 , Z 8 , Z 4 , Z 2 , Z 1 ), где Z n представляет π / n радианная вращательная симметрия.
Джон Конвей обозначает эти низшие симметрии буквой, и порядок симметрии следует за буквой. [6] r20000 означает полную симметрию, а a1 означает отсутствие симметрии. Он дает d (диагональ) с зеркальными линиями, проходящими через вершины, p с зеркальными линиями, проходящими через края (перпендикулярно), i с зеркальными линиями, проходящими как через вершины, так и через края, и g для вращательной симметрии.
Эта более низкая симметрия дает степень свободы в определении неправильных многоугольников. Только подгруппа g10000 не имеет степеней свободы, но ее можно рассматривать как направленные ребра .
Мириаграмма
[ редактировать ]Мириаграмма – это звездчатый многоугольник с 10 000 сторонами . Есть 1999 регулярных форм. [а] задается символами Шлефли формы {10000/ n }, где n — целое число от 2 до 5000, взаимно простое с 10 000. также находятся 3000 обычных фигурок звезд В остальных корпусах .
В популярной культуре
[ редактировать ]В новелле «Флатландия» предполагается, что Главный круг имеет десять тысяч сторон, что делает его мириагоном.
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ 5000 случаев - 1 (выпуклый) - 1000 (кратный 5) - 2500 (кратный 2) + 500 (кратный 2 и 5)
Ссылки
[ редактировать ]- ^ Медитация VI Декарта (английский перевод).
- ^ Ипполит Тэн, Об интеллекте : стр. 9–10.
- ^ Жак Маритен, Введение в философию : стр. 108.
- ^ Алан Нельсон (ред.), Товарищ по рационализму : стр. 285.
- ^ Паоло Фабиани, Философия воображения в Вико и Мальбранше : с. 222.
- ^ Симметрии вещей , Глава 20
