Поверхность текучести

Поверхность текучести — это пятимерная поверхность в шестимерном пространстве напряжений . Поверхность текучести обычно выпуклая , а напряженное состояние внутри поверхности текучести является упругим. Когда напряженное состояние лежит на поверхности, говорят, что материал достиг предела текучести и стал пластичным . Дальнейшая деформация материала приводит к тому, что напряженное состояние сохраняется на поверхности текучести, хотя форма и размер поверхности могут меняться по мере развития пластической деформации. Это связано с тем, что напряженные состояния, лежащие за пределами поверхности текучести, недопустимы для пластичности, не зависящей от скорости , но не в некоторых моделях вязкопластичности . [ 1 ]
Поверхность текучести обычно выражается (и визуализируется) в трехмерном пространстве главных напряжений ( ), двух- или трехмерное пространство, натянутое на инварианты напряжений ( ) или версию трехмерного пространства напряжений Хейга – Вестергора . Таким образом, мы можем записать уравнение поверхности текучести (то есть функции доходности) в виде:
- где являются главными напряжениями.
- где является первым главным инвариантом напряжения Коши и – второй и третий главные инварианты девиаторной части напряжения Коши.
- где представляют собой масштабированные версии и и является функцией .
- где представляют собой масштабированные версии и , и это угол напряжения [ 2 ] или угол Лоде [ 3 ]
Инварианты, используемые для описания поверхностей текучести
[ редактировать ]
Первый главный инвариант ( ) напряжения Коши ( ), а также второй и третий главные инварианты ( ) девиаторной части ( ) напряжения Коши определяются как:
где ( ) являются основными значениями , ( ) являются основными значениями , и
где является единичной матрицей.
Связанный набор величин ( ), обычно используются для описания поверхностей текучести когезионных фрикционных материалов, таких как камни, почвы и керамика. Они определяются как
где эквивалентное напряжение . Однако возможность отрицательных значений и полученное воображаемое делает использование этих величин проблематичным на практике.
Другой родственный набор широко используемых инвариантов: ( ), описывающие цилиндрическую систему координат ( координаты Хейга–Вестергора ). Они определяются как:
The плоскость также называют плоскостью Рендулика . Угол называется углом напряжения, величина иногда называют параметром Лоде [ 4 ] [ 5 ] [ 6 ] и отношения между и впервые дано Новожиловым В.В. в 1951 г., [ 7 ] см. также [ 8 ]
Главные напряжения и координаты Хейга – Вестергора связаны соотношением
В литературе можно встретить и другое определение угла Лоде: [ 9 ]
в этом случае упорядоченные главные напряжения (где ) связаны соотношением [ 10 ]
Примеры поверхностей текучести
[ редактировать ]В технике известно несколько различных поверхностей текучести, наиболее популярные перечислены ниже.
Поверхность текучести Tresca
[ редактировать ]Критерий доходности Треска считается работой Анри Треска . [ 11 ] Она также известна как максимального напряжения сдвига теория (MSST) и теория Треска – Геста. [ 12 ] (ТГ) критерий. В терминах главных напряжений критерий Треска выражается как
Где - предел текучести при сдвиге, а - предел текучести при растяжении.
На рис. 1 показана поверхность текучести Трески–Геста в трехмерном пространстве главных напряжений. Это призма с шестью сторонами и бесконечной длиной. Это означает, что материал остается эластичным, когда все три главных напряжения примерно эквивалентны ( гидростатическое давление ), независимо от того, насколько сильно он сжимается или растягивается. Однако когда одно из главных напряжений становится меньше (или больше), чем другие, материал подвергается сдвигу. В таких ситуациях, если напряжение сдвига достигает предела текучести, материал переходит в пластическую область. На рис. 2 показана поверхность текучести Трески–Геста в двумерном пространстве напряжений, она представляет собой сечение призмы по самолет.


поверхность текучести фон Мизеса
[ редактировать ]Критерий текучести фон Мизеса выражается в главных напряжениях как
где – предел текучести при одноосном растяжении.
На рис. 3 показана поверхность текучести фон Мизеса в трехмерном пространстве главных напряжений. Это круглый цилиндр бесконечной длины, ось которого наклонена под равными углами к трем главным напряжениям. На рис. 4 показана поверхность текучести фон Мизеса в двумерном пространстве в сравнении с критерием Трески-Геста. Сечение цилиндра Мизеса плоскостью создает эллиптическую форму поверхности текучести.


Критерий Буржинского-Ягна
[ редактировать ]представляет собой общее уравнение поверхности вращения второго порядка вокруг гидростатической оси. Некоторые особые случаи: [ 15 ]
- цилиндр (Максвелл (1865 г.), Хубер (1904 г.), фон Мизес (1913 г.), Хенки (1924 г.)),
- конус (Botkin (1940), Drucker-Prager (1952), Mirolyubov (1953)),
- параболоид (Буржинский (1928), Баландин (1937), Торре (1947)),
- эллипсоид с центром в плоскости симметрии , (Бельтрами (1885)),
- эллипсоид с центром в плоскости симметрии с (Шлейхер (1926)),
- гиперболоид из двух листов (Буржинский (1928), Ягн (1931)),
- однолистный гиперболоид с центром в плоскости симметрии , , (Кун (1980))
- однолистный гиперболоид , (Филоненко-Бородич (1960), Гольденблат-Копнов (1968), Филин (1975)).
Отношения сжатия-растяжения и кручения-растяжения можно вычислить как
Коэффициенты Пуассона при растяжении и сжатии получают с помощью
Для пластичных материалов ограничение
важно. Применение вращательно-симметричных критериев хрупкого разрушения с
изучено недостаточно. [ 16 ]
Критерий Буржинского-Ягна хорошо подходит для академических целей. Для практических приложений в уравнение следует ввести третий инвариант девиатора в нечетной и четной степени, например: [ 17 ]
критерий Губера
[ редактировать ]Критерий Хубера состоит из эллипсоида Бельтрами и масштабированного цилиндра фон Мизеса в пространстве главных напряжений: [ 18 ] [ 19 ] [ 20 ] [ 21 ] см. также [ 22 ] [ 23 ]
с . Переход между поверхностями в поперечном сечении непрерывно дифференцируема. Критерий представляет собой «классический взгляд» на поведение неупругого материала:
- поведение материала, чувствительного к давлению, для с и
- нечувствительное к давлению поведение материала для с
Критерий Хубера можно использовать в качестве поверхности текучести с эмпирическим ограничением на коэффициент Пуассона при растяжении. , что приводит к .
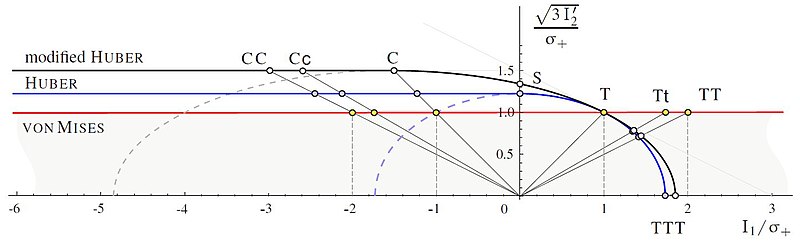
Модифицированный критерий Хубера, [ 24 ] [ 23 ] см. также, [ 25 ] ср. [ 26 ]
состоит из эллипсоида Шлейхера с ограничением коэффициента Пуассона при сжатии
и цилиндр с -переход в сечении . Вторая настройка параметров и следует соотношение сжатия/растяжения
Модифицированный критерий Хубера может лучше соответствовать измеренным данным, чем критерий Хубера. Для настройки следует и .
Критерий Хубера и модифицированный критерий Хубера следует отдать предпочтение критерию фон Мизеса, поскольку они позволяют получить более безопасные результаты в области . Для практических приложений третий инвариант девиатора следует учитывать в этих критериях. [ 23 ]
Поверхность текучести Мора – Кулона
[ редактировать ]Критерий текучести (разрушения) Мора -Кулона аналогичен критерию Треска с дополнительными положениями для материалов с различным пределом текучести при растяжении и сжатии. Эта модель часто используется для моделирования бетона , грунта или сыпучих материалов . Критерий текучести Мора – Кулона можно выразить как:
где
и параметры и – напряжения текучести (разрушения) материала при одноосном сжатии и растяжении соответственно. Формула сводится к критерию Треска, если .
На рис. 5 показана поверхность текучести Мора–кулона в трехмерном пространстве главных напряжений. Это коническая призма и определяет угол наклона конической поверхности. На рисунке 6 показана поверхность текучести Мора – Кулона в двумерном пространстве напряжений. На рисунке 6 и используется для и соответственно в формуле. Это сечение этой конической призмы в плоскости . На рисунке 6 Rr и Rc используются в формуле для Syc и Syt соответственно.


Поверхность текучести Друкера – Прагера
[ редактировать ]Критерий текучести Друкера -Прагера аналогичен критерию текучести фон Мизеса с возможностью работы с материалами с различным пределом текучести при растяжении и сжатии. Этот критерий чаще всего используется для бетона , где разрушение могут определять как нормальные, так и сдвиговые напряжения. Критерий доходности Друкера-Прагера можно выразить как
где
и , – одноосные напряжения текучести при сжатии и растяжении соответственно. Формула сводится к уравнению фон Мизеса, если .
На рис. 7 показана поверхность текучести Друкера–Прагера в трехмерном пространстве главных напряжений. Это обычный конус . На рисунке 8 показана поверхность текучести Друкера-Прагера в двумерном пространстве. Эллиптическая упругая область представляет собой поперечное сечение конуса на плоскости ; его можно выбрать так, чтобы оно пересекало поверхность текучести Мора – Кулона в разном количестве вершин. Одним из вариантов является пересечение поверхности текучести Мора – Кулона в трех вершинах по обе стороны от поверхности текучести Мора – Кулона. линии, но обычно выбираются по соглашению как те, которые находятся в режиме сжатия. [ 27 ] Другой вариант — пересечение поверхности текучести Мора – Кулона в четырех вершинах по обеим осям (одноосная посадка) или в двух вершинах по диагонали. (двухосная посадка). [ 28 ] Критерий текучести Друкера-Прагера также обычно выражается через сцепление материала и угол трения .


Поверхность текучести Бреслера – Пистера
[ редактировать ]Критерий текучести Бреслера-Пистера является расширением критерия текучести Друкера Прагера , который использует три параметра и имеет дополнительные условия для материалов, которые текучесть при гидростатическом сжатии. В терминах главных напряжений этот критерий текучести можно выразить как
где являются материальными константами. Дополнительный параметр придает поверхности текучести эллипсоидное поперечное сечение, если смотреть с направления, перпендикулярного ее оси. Если – предел текучести при одноосном сжатии, - предел текучести при одноосном растяжении, а – предел текучести при двухосном сжатии, параметры можно выразить как


Поверхность текучести Виллама – Варнке
[ редактировать ]Критерий текучести Виллама-Варнке представляет собой трехпараметрическую сглаженную версию критерия текучести Мора-Кулона , которая по форме похожа на критерии текучести Друкера-Прагера и Бреслера-Пистера .
Критерий доходности имеет функциональный вид
Однако чаще всего это выражается в координатах Хейга – Вестергора как
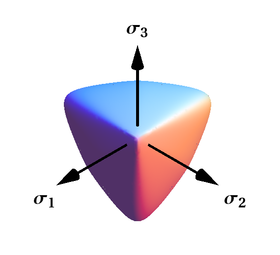
Поперечное сечение поверхности, если смотреть вдоль ее оси, представляет собой сглаженный треугольник (в отличие от Мора–Кулона). Поверхность текучести Виллама – Варнке выпукла и имеет уникальные и четко определенные первую и вторую производные в каждой точке своей поверхности. Таким образом, модель Уиллама-Варнке является вычислительно надежной и использовалась для различных когезионно-фрикционных материалов.


Тригонометрические поверхности текучести Подгурского и Розендаля
[ редактировать ]Нормированные по одноосному растягивающему напряжению , критерий Подгорского [ 29 ] как функция угла напряжения читает
с функцией формы тригональной симметрии в -самолет
Он содержит критерии фон Мизеса (кружок в -самолет, , ), Треска (правильный шестиугольник, , ), Мариотта (правильный треугольник, , ), Ивлев [ 30 ] (правильный треугольник, , ), а также кубический критерий Сайра [ 31 ] (критерий Оттосена [ 32 ] ) с и изотоксальные (равносторонние) шестиугольники критерия Капурсо [ 30 ] [ 31 ] [ 33 ] с . Переход фон Мизес — Треска [ 34 ] следует с , . Изогональные (равноугольные) шестиугольники критерия Хейторнтвейта [ 23 ] [ 35 ] [ 36 ] содержащий критерий Шмидта-Ишлинского (правильный шестиугольник), не может быть описан критерием Подгорского.
Критерий Розендаля [ 37 ] [ 38 ] читает
с функцией формы гексагональной симметрии в -самолет
Он содержит критерии фон Мизеса (кружок, , ), Треска (правильный шестиугольник, , ), Шмидта—Ишлинского (правильный шестиугольник, , ), Соколовский (правильный двенадцатиугольник, , ), а также бикубический критерий [ 23 ] [ 37 ] [ 39 ] [ 40 ] с или наравне с и изотоксальные додекагоны единого критерия текучести Ю. [ 41 ] с . Изогональные додекагоны мультипликативного анзац-критерия гексагональной симметрии [ 23 ] содержащая критерий Ишлинского-Ивлева (правильный двенадцатиугольник), не может быть описана критерием Розендаля.
Критерии Подгорского и Розендаля описывают одиночные поверхности в пространстве главных напряжений без каких-либо дополнительных внешних контуров и пересечений плоскостей. Обратите внимание, что во избежание числовых проблем функция реальной части можно ввести в функцию формы: и . Обобщение в форме [ 37 ] актуальна для теоретических исследований.
Чувствительное к давлению расширение критериев можно получить с помощью линейного -замена [ 23 ]
этого достаточно для многих применений, например, металлов, чугуна, сплавов, бетона, неармированных полимеров и т. д.

Поверхность текучести Бигони – Пикколороаза
[ редактировать ]Критерий текучести Бигони -Пикколоаза. [ 42 ] [ 43 ] представляет собой семипараметрическую поверхность, определяемую формулой
где это функция «меридиана»
описывающая чувствительность к давлению и это «девиаторная» функция [ 44 ]
описывающее зависимость текучести от Лоде. Семь неотрицательных материальных параметров:
определяют форму меридианного и девиаторного участков.
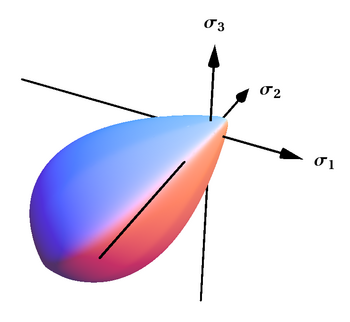
Этот критерий представляет собой гладкую и выпуклую поверхность, замкнутую как при гидростатическом растяжении, так и при сжатии и имеющую каплевидная форма, особенно подходящая для описания фрикционных и зернистых материалов. Этот критерий был обобщен и на случай поверхностей с углами. [ 45 ]
Косинусный подход (Альтенбах-Болчоун-Колупаев)
[ редактировать ]Для формулировки критериев прочности угол напряжения
можно использовать.
Следующий критерий изотропного поведения материала
содержит ряд других известных, менее общих критериев при условии выбора подходящих значений параметров.
Параметры и описать геометрию поверхности -самолет. Они подчиняются ограничениям
которые следуют из условия выпуклости. Более точная формулировка третьего ограничения предложена в . [ 46 ] [ 47 ]
Параметры и описать положение точек пересечения поверхности текучести с гидростатической осью (диагональ пространства в пространстве главных напряжений). Эти точки пересечения называются гидростатическими узлами. В случае материалов, которые не разрушаются при гидростатическом давлении (сталь, латунь и т. д.), получают . В противном случае для материалов, которые разрушаются при гидростатическом давлении (твердые пенопласты, керамика, спеченные материалы и т. д.), следует .
Целые степени и , описать кривизну меридиана. Меридиан с. представляет собой прямую линию и с – притча.
Поверхность текучести Барлата
[ редактировать ]Для анизотропных материалов в зависимости от направления применяемого процесса (например, прокатки) механические свойства изменяются, и поэтому использование анизотропной функции текучести имеет решающее значение. С 1989 года Фредерик Барла разработал семейство функций текучести для материального моделирования пластической анизотропии. Среди них критерии текучести Yld2000-2D применялись для широкого спектра листового металла (например, алюминиевых сплавов и современных высокопрочных сталей). Модель Yld2000-2D представляет собой функцию текучести неквадратичного типа, основанную на двух линейных преобразованиях тензора напряжений:
- :

Локусы урожайности Yld2000-2D для листа AA6022 T4. - где это эффективный стресс. и и — преобразованные матрицы (линейным преобразованием C или L):
- где s – тензор девиаторных напряжений.
для главных значений X' и X», модель можно выразить следующим образом:
и:
где — это восемь параметров модели Барлата Yld2000-2D, которые необходимо определить с помощью серии экспериментов.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Симо, Дж.С. и Хьюз, Т. JR, (1998), Вычислительная неэластичность, Springer.
- ^ Ю, М.-Х. (2004), Единая теория прочности и ее приложения . Шпрингер, Берлин
- ^ Зенкевич О.К., Панде, Г.Н. (1977), Некоторые полезные формы изотропных поверхностей текучести для почвы и рок-механика. В: Гудехус, Г. (ред.) Конечные элементы в геомеханике . Уайли, Нью-Йорк, стр. 179–198.
- ^ Лоде, В. (1925). Эксперименты по влиянию среднего главного напряжения на предел текучести. ЗАММ 5 (2), стр. 142–144.
- ^ Лоде, В. (1926). Эксперименты по влиянию среднего главного напряжения на течение металлов железа, меди и никеля . Газета «Физ. , том. 36, стр. 913–939.
- ^ Лоде, В. (1928). Влияние среднего главного напряжения на течение металлов . Диссертация, Геттингенский университет. Научно-исследовательская работа в области машиностроения, выпуск 303, VDI, Берлин
- ^ Novozhilov, V.V. (1951). On the principles of the statical analysis of the experimental results for isotropic materials (in Russ.: O prinzipakh obrabotki rezultatov staticheskikh ispytanij izotropnykh materialov). Prikladnaja Matematika i Mekhanika , XV(6):709–722.
- ^ Наяк, GC и Зенкевич, OC (1972). Удобные формы инвариантов напряжений для пластичности . Труды журнала структурного отдела ASCE, том. 98, нет. ST4, стр. 949–954.
- ^ Чакрабарти, Дж., 2006, Теория пластичности: третье издание , Elsevier, Амстердам.
- ^ Брэннон, Р.М., 2009, КАЙЕНТА: Теория и руководство пользователя , Национальные лаборатории Сандии, Альбукерке, Нью-Мексико.
- ^ Треска, Х. (1864). Память о течении твердых тел, подвергающихся высокому давлению. ЧР акад. наук. Париж, том. 59, с. 754.
- ^ Гость
- ^ Буржинский, В. (1929). О гипотезах усилий . Schweizerische Bauzeitung, 94 (21), стр. 259–262.
- ^ Yagn, Yu. I. (1931). New methods of strength prediction (in Russ.: Novye metody pascheta na prochnost') . Vestnik inzhenerov i tekhnikov, 6, pp. 237–244.
- ^ Альтенбах, Х., Колупаев, В.А. (2014) Классические и неклассические критерии разрушения, в Альтенбах, Х., Садовски, Т., ред., Анализ отказов и повреждений современных материалов , в печати, Springer, Гейдельберг (2014). ), стр. 1–66.
- ^ Беляев, Н.М. (1979). Сопротивление материалов . Издательство «Мир», Москва
- ^ Больчоун А., Колупаев В.А., Альтенбах Х. (2011) Выпуклые и невыпуклые поверхности текучести (на немецком языке: Konvexe und nichtkonvexe Fliessseiten), Research in Engineering , 75 (2), стр. 73–92.
- ^ Хубер, MT (1904). Удельная деформационная работа как мера материальных усилий (на польском языке: Правильная деформационная работа как мера материальных усилий), Технический журнал , Львов, Орган Львовского политехнического общества, т. 22. с. 34-40, 49-50, 61-62, 80-81
- ^ Фёппль, А., Фёппль, Л. (1920). Побуждение и принуждение: высшая теория силы для инженеров . Р. Ольденбург, Мюнхен
- ^ Буржинский, В. (1929). О гипотезах усилий. Швейцарская строительная газета 94 (21): 259–262
- ^ Кун, П. (1980). Основные черты гипотезы общей силы , отрывок из вступительной лекции автора от 11 июля 1980 г. О конструкторе и гипотезах прочности. Институт машиностроения, Карлсруэ
- ^ Колупаев В.А., Монеке М., Беккер Ф. (2004). Появление напряжений при ползучести. Расчет пластиковые детали (по-немецки: выражение напряжений при ползучести: расчет пластиковых компонентов). Пластмассы 94(11):79–82
- ^ Перейти обратно: а б с д и ж г Колупаев, В.А. (2018). Концепция эквивалентного напряжения для анализа предельного состояния , Springer, Cham.
- ^ Колупаев, В.А., (2006). 3D ползучесть деталей из неармированных термопластов (на немецком языке: Трехмерная ползучесть деталей из неармированных термопластов) , дисс., Университет Мартина Лютера Галле-Виттенберг, Галле-Заале
- ^ Мемхард, Д., Андриё, Ф., Сан, Д.-З., Хакер, Р. (2011) Разработка и проверка модели материала для прогнозирования безопасности локализации выхлопных турбокомпрессоров, 8-я Европейская конференция пользователей LS-DYNA , Страсбург, май 2011 г., 11 стр.
- ^ ДиМаджио, Флорида, Сэндлер, И.С. (1971) Модель материала для зернистых грунтов, Журнал отдела инженерной механики , 97 (3), 935-950
- ^ Хан и Хуан. (1995), Континуальная теория пластичности. Дж.Уайли.
- ^ Нето, Перич, Оуэн. (2008), Математическая теория пластичности. Дж. Уайли.
- ^ Подгорский, Дж. (1984). Условие предельного состояния и функция диссипации изотропных материалов, Архив механики 36 (3), стр. 323-342.
- ^ Перейти обратно: а б Ivlev, D. D. (1959). The theory of fracture of solids (in Russ.: K teorii razrusheniia tverdykh tel), J. of Applied Mathematics and Mechanics , 23(3), pp. 884-895.
- ^ Перейти обратно: а б Сайир, М. (1970). О текучести теории пластичности, Ingenieur-Archiv 39(6), стр. 414-432.
- ^ Оттосен, Н.С. (1975). Разрушение и эластичность бетона, Датская комиссия по атомной энергии , Научно-исследовательский институт Рисо, Инженерный отдел, Отчет Рисо-М-1801, Роскилле.
- ^ Капурсо, М. (1967). Условия текучести несжимаемых изотропных и ортотропных материалов с различным пределом текучести при растяжении и сжатии, Meccanica 2(2), стр. 118-125.
- ^ Леметр Дж., Шабош Дж.Л. (1990). Механика твердых материалов , Издательство Кембриджского университета, Кембридж.
- ^ Кэндланд, Коннектикут (1975). Значение макроскопических критериев разрушения, не зависящих от гидростатического напряжения, Int. J. Fracture 11 (3), стр. 540–543.
- ^ Хейторнтвейт RM (1961). Диапазон условий текучести при идеальной пластичности, Proc ASCE J Eng Mech Div , EM6, 87, стр. 117–133.
- ^ Перейти обратно: а б с Розендаль, П.Л., Колупаев, В.А., Альтенбах, Х. (2019). Показатели предельного предела текучести для универсальных критериев прочности, под ред. Альтенбаха Х., Окснера А., « Состояние искусства и будущие тенденции в моделировании материалов» , «Усовершенствованные структурированные материалы STRUCTMAT», Springer, Cham, стр. 259–324.
- ^ Розендаль, Польша (2020). От объема к структурному разрушению: Разрушение гиперупругих материалов , Дисс., Технический университет Дармштадта.
- ^ Швед, А. (2000). Гипотезы прочности и определяющие соотношения материалов, включая эффекты деградации, докторская диссертация, Факультет гражданского строительства, Варшавский технологический университет, Варшава.
- ^ Лагздин, А. (1997). Гладкие выпуклые предельные поверхности в пространстве симметричных тензоров второго ранга, Механика композиционных материалов , 3(2), 119-127.
- ^ Ю М.-Х. (2002). Достижения в теории прочности материалов в условиях сложного напряженного состояния в 20 веке, Applied Mechanics Reviews , 55 (5), стр. 169-218.
- ^ Бигони, Д. Нелинейная механика твердого тела: теория бифуркаций и нестабильность материала. Издательство Кембриджского университета, 2012. ISBN 9781107025417 .
- ^ Бигони Д. и Пикколроаз А. (2004), Критерии текучести квазихрупких и фрикционных материалов, Международный журнал твердых тел и структур 41 , 2855–2878.
- ^ Подгорский, Дж. (1984). Условие предельного состояния и функция диссипации для изотропных материалов. Архив механики , 36 (3), стр. 323–342.
- ^ Пикколроаз, А. и Бигони, Д. (2009), Критерии текучести квазихрупких и фрикционных материалов: обобщение на поверхности с углами, Международный журнал твердых тел и структур 46 , 3587–3596.
- ^ Альтенбах Х., Болчоун А., Колупаев В.А. (2013). Феноменологические критерии текучести и разрушения, под ред. Альтенбаха Х., Окснера А., «Пластичность материалов, чувствительных к давлению» , Серия ASM, Springer, Гейдельберг, стр. 49–152.
- ^ Колупаев, В.А. (2018). Концепция эквивалентного напряжения для анализа предельного состояния, Springer, Cham.



















![{\displaystyle {\begin{aligned}I_{1} &={\text{Tr}}({\boldsymbol {\sigma }})=\sigma _{1}+\sigma _{2}+\sigma _ {3}\\J_{2}&={\tfrac {1}{2}}{\boldsymbol {s}}:{\boldsymbol {s}}={\tfrac {1}{6}}\left[(\sigma _{1}-\sigma _{2})^{2}+(\sigma _{2}-\sigma _{3})^{2}+ (\sigma _{3}-\sigma _{1})^{2}\right]\\J_{3}&=\det({\boldsymbol {s}})={\tfrac {1}{3}}({\boldsymbol {s}}\cdot {\boldsymbol {s}}):{\boldsymbol {s}}=s_{1}s_{2}s_{3}\end{aligned }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2367aae106ad4915a3c05e829c4d06e62ee17c18)





















![{\displaystyle \gamma _{1} =\gamma _{2}\in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66ab6f7a14a52c2042d17030aa16705df21f1541)
![{\displaystyle \gamma _{1}\in ]0,1[,\gamma _{2}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab67fc470c16fd7d16b50462f9c9d7af9b70f566)

![{\displaystyle \gamma _{1} = - \gamma _{2}\in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19f234ad4d2cddbc2eb4b2b5c0dfcb2a128c275b)

![{\displaystyle \gamma _{1}\in ]0,1[,\gamma _{2}<0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc95c96fba08cb97251ef453346323702300f9ab)
![{\displaystyle \gamma _{1}\in ]0,1[,\gamma _{2}\in ]0,\gamma _{1}[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bdf157e5b65de316f3462bcb5e2de9d10cda1cb)






![{\displaystyle \nu _{+}^{\mathrm {in} }\in {\bigg [}\,0,48,\,{\frac {1}{2}}\,{\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b7c270b90d3c766fd6ecd9b7204e1622d9f7722)
![{\displaystyle \nu _{+}^{\mathrm {in} }\in ]-1,~\nu _{+}^{\mathrm {el} }\,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/690096f2ce81fb70324e3cebefabb993721ed772)

![{\displaystyle 3\,I_{2}'=\left\{{\begin{array}{ll} \displaystyle {\frac {\sigma _{\mathrm {eq} }-\gamma _{1}\, I_{1}}{1-\gamma _{1}}}\,{\frac {\sigma _{\mathrm {eq} }+\gamma _{1}\,I_{1}}{1+\gamma _{1}}},&I_{1}>0\\[1em]\displaystyle {\frac {\sigma _{\mathrm {eq} } }{1-\gamma _{1}}}\,{\frac {\sigma _{\mathrm {eq} }}{1+\gamma _{1}}},&I_{1}\leq 0\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84e5badc1256fedb02c6e3bb4e32c3c04f455c74)


![{\displaystyle \nu _{+}^{\mathrm {in} }\in \left]-1,\,1/2\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0492b09eaa5450be7f96f4a04b025a37ef0a620)


![{\displaystyle \nu _{+}^{\mathrm {in}}\in [0,48,1/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95b2a945c4242aba4b539c51f5dc7441fceda3b9)
![{\displaystyle \gamma _{1}\in [0,0,1155]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bee6b21ec154dddb4479a8f5fc3321c72ec824f4)





![{\displaystyle 3\,I_{2}'=\left\{{\begin{array}{ll} \displaystyle {\frac {\sigma _{\mathrm {eq} }-\gamma _{1}\, I_{1}}{1-\gamma _{1}}}\,{\frac {\sigma _{\mathrm {eq} }-\gamma _{2}\,I_{1}}{1-\gamma _{2}}},&I_{1}>-d\,\sigma _{\mathrm {+} }\\[1em]\displaystyle { \frac {\sigma _{\mathrm {eq} }^{2}}{(1-\gamma _{1}-\gamma _{2})^{2}}},&I_{1}\leq -d\,\sigma _{\mathrm {+} }\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7665d54a30d98465586f222a2ad1cf088bfd4d2a)






















![{\displaystyle S_{yc}={\tfrac {1}{\sqrt {2}}}\left[(\sigma _{1}-\sigma _{2})^{2}+(\sigma _{ 2}-\sigma _{3})^{2}+(\sigma _{3}-\sigma _{1})^{2}\right]^{1/2}-c_{0}-c_{1}~(\sigma _{1}+\sigma _{2}+\sigma _{3} )-c_{2}~(\sigma _{1}+\sigma _{2}+\sigma _{3})^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/168ce31fef86a9a05a75721a81e088c69edcf24f)











![{\displaystyle \Omega _{3}(\theta,\beta _{3},\chi _{3})=\cos \left[\displaystyle {\frac {1}{3}}\left(\pi \beta _{3}-\arccos[\,\sin(\chi _{3}\,{\frac {\pi }{2}})\,\!\cos 3\,\theta \,]\right)\right],\qquad \beta _{3}\in [0,\,1],\quad \chi _{3}\in [-1,\,1 ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31655f9e540e841ea6d966f7a0bdbe1fd6304b4a)
![{\displaystyle \beta _{3}=[0,\,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20634c0926a05259beda78f4e18b1ea6d38621be)





![{\displaystyle \chi _{3}=[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b4456eca66f88480bde86583de8ac126d973ac4)

![{\displaystyle \Omega _{6}(\theta,\beta _{6},\chi _{6})=\cos \left[\displaystyle {\frac {1}{6}}\left(\pi \beta _{6}-\arccos[\,\sin(\chi _{6}\,{\frac {\pi }{2}})\,\!\cos 6\,\theta \,]\right)\right],\qquad \beta _{6}\in [0,\,1],\quad \chi _{6}\in [-1,\,1 ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e980c867fa1766fcc5a741ecf363e19c05a8bfe8)
![{\displaystyle \beta _{6}=[0,\,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61f7b566943062df913486ad99edfa445fbb58a1)














![{\displaystyle F(p)=\left\{{\begin{array}{ll}-Mp_{c}{\sqrt {(\phi -\phi ^{m})[2(1-\alpha)\ phi +\alpha ]}},&\phi \in [0,1],\\+\infty ,&\phi \notin [0,1],\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9948aa54df1e39ab115e425b19f088dff39beadc)


![{\displaystyle g(\theta)={\frac {1}{\cos[\beta {\frac {\pi }{6}}-{\frac {1}{3}}\cos ^{-1} (\гамма \cos 3\тета )]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dba97f3c7548243d55f4c6736d862e34b31b04cb)





















![{\displaystyle \left[{\begin{array}{*{20}{c}}{{L'}_{11}}\\{{L'}_{12}}\\{{L'}_{21 }}\\{{L'}_{22}}\\{{L'}_{66}}\end{array}}\right]=\left[{\begi n{array}{*{20}{c}}{2/3}&0&0\\{-1/3}&0&0\\0&{-1/3}&0\\0&{-2/3}&0\\ 0&0&1\end{array}}\right]\left[{\begin{array}{*{20}{c}}{\alpha _{1}}\\{\альфа _{2}}\\{\альфа _{7}}\end{array}}\right],\left[{\begin{array}{*{20}{c}}{{L''}_{11}}\\{{L' '}_ {12}}\\{{L''}_{21}}\\{{L''}_{22}}\\{{L''}_{66}}\end{array}}\ вправо]=\влево[{\быть gin{array}{*{20}{c}}{-2}&2&8&{-2}&0\\1&{-4}&{-4}&4&0\\4&{-4}&{-4}&4&0\ \{-2}& 8&2&{-2}&0\\0&0&0&0&1\end{array}}\right]\left[{\begin{array}{*{20}{c}}{\alpha _{3}}\\{\alpha _{4}}\\{\alpha _{5}}\\{\alpha _{6}}\\{\alpha _{8}}\end{array} }\верно]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ad31d6027e7e5da286c1ec7579505cffa4c919c)
