Ферми-газ

Ферми -газ — это идеализированная модель, ансамбль множества невзаимодействующих фермионов . Фермионы — это частицы , которые подчиняются статистике Ферми-Дирака , такие как электроны , протоны и нейтроны , и, в общем, частицы с полуцелым спином . Эта статистика определяет энергетическое распределение фермионов в ферми-газе в тепловом равновесии и характеризуется их плотностью числа , температурой и набором доступных энергетических состояний. Модель названа в честь итальянского физика Энрико Ферми .

Эта физическая модель полезна для некоторых систем со многими фермионами. Некоторыми ключевыми примерами являются поведение носителей заряда в металле , нуклонов в атомном ядре , нейтронов в нейтронной звезде и электронов в белом карлике .

Описание

Идеальный ферми-газ или свободный ферми-газ — это физическая модель, предполагающая совокупность невзаимодействующих фермионов в постоянной потенциальной яме . Фермионы — это элементарные или составные частицы с полуцелым спином, что соответствует статистике Ферми – Дирака . Эквивалентная модель для частиц с целым спином называется бозе-газом (ансамблем невзаимодействующих бозонов ). При достаточно низкой плотности числа частиц и высокой температуре и ферми-газ, и бозе-газ ведут себя как классический идеальный газ .

Согласно принципу Паули , ни одно квантовое состояние не может быть занято более чем одним фермионом с одинаковым набором квантовых чисел . Таким образом, невзаимодействующий ферми-газ, в отличие от бозе-газа, концентрирует небольшое количество частиц на энергию. Таким образом, ферми-газу запрещено конденсироваться в конденсат Бозе-Эйнштейна , хотя слабо взаимодействующие ферми-газы могут образовывать куперовскую пару и конденсат (также известный как режим кроссовера BCS -BEC). Полная энергия ферми-газа при абсолютном нуле больше, чем сумма одночастичных основных состояний , поскольку принцип Паули предполагает своего рода взаимодействие или давление, которое удерживает фермионы разделенными и движущимися. По этой причине давление ферми-газа не равно нулю даже при нулевой температуре, в отличие от давления классического идеального газа. Например, это так называемое давление вырождения стабилизирует нейтронную звезду (ферми-газ нейтронов) или звезду белого карлика (ферми-газ электронов) против внутреннего притяжения силы тяжести , которое якобы могло бы коллапсировать звезду в черную дыру . Только когда звезда достаточно массивна, чтобы преодолеть давление вырождения, она может коллапсировать в сингулярность.

Можно определить температуру Ферми, ниже которой газ можно считать вырожденным (его давление почти исключительно вытекает из принципа Паули). Эта температура зависит от массы фермионов и плотности энергетических состояний .

Основное предположение модели свободных электронов для описания делокализованных электронов в металле можно вывести из ферми-газа. взаимодействиями пренебрегают Поскольку из-за эффекта экранирования , задача рассмотрения равновесных свойств и динамики идеального ферми-газа сводится к изучению поведения одиночных независимых частиц. В этих системах температура Ферми обычно составляет многие тысячи Кельвинов , поэтому в человеческих приложениях электронный газ можно считать вырожденным. Максимальная энергия фермионов при нулевой температуре называется энергией Ферми . Энергетическая поверхность Ферми в обратном пространстве известна как поверхность Ферми .

Модель почти свободных электронов модель ферми-газа для рассмотрения кристаллической структуры металлов адаптирует и полупроводников , где электроны в кристаллической решетке заменяются блоховскими электронами с соответствующим кристаллическим импульсом . Таким образом, периодические системы все еще относительно послушны, и модель служит отправной точкой для более продвинутых теорий, касающихся взаимодействий, например, с использованием теории возмущений .

1D однородный газ

Одномерная бесконечная квадратная яма длиной L представляет собой модель одномерного ящика с потенциальной энергией: $$V(x)={\begin{cases}0,&x_{c}-{\tfrac {L}{2}}<x<x_{c}+{\tfrac {L}{2}},\\\infty ,&{\text{otherwise.}}\end{cases}}$$

Это стандартная модельная система в квантовой механике, для которой хорошо известно решение для одной частицы. Поскольку потенциал внутри ящика однороден, эту модель называют одномерным однородным газом. даже несмотря на то, что фактический профиль числовой плотности газа может иметь узлы и пучности, когда общее количество частиц невелико.

Уровни помечены одним квантовым числом n , а энергии определяются как:

$$E_{n}=E_{0}+{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}.$$где $E_{0}$ — энергия нулевой точки (которая может быть выбрана произвольно как форма фиксации калибровки ), $m$ масса одного фермиона и $\hbar$ – приведенная постоянная Планка .

Для N фермионов со спин- 1 ⁄ 2 в ящике, не более двух частиц могут иметь одинаковую энергию, т. е. две частицы могут иметь энергию ${\textstyle E_{1}}$, две другие частицы могут иметь энергию ${\textstyle E_{2}}$ и так далее. Две частицы одинаковой энергии имеют спин 1 ⁄ 2 (раскрутка вверх) или - 1 ⁄ 2 (спин вниз), что приводит к двум состояниям на каждом энергетическом уровне. В конфигурации, для которой полная энергия наименьшая (основное состояние), все энергетические уровни до n = N /2 заняты, а все более высокие уровни пусты.

Определение эталона для энергии Ферми $E_{0}$, поэтому энергия Ферми определяется выражением $$E_{\mathrm {F} }^{({\text{1D}})}=E_{n}-E_{0}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left(\left\lfloor {\frac {N}{2}}\right\rfloor \right)^{2},$$где ${\textstyle \left\lfloor {\frac {N}{2}}\right\rfloor }$ — это функция пола , оцениваемая при n = N /2.

Термодинамический предел

В термодинамическом пределе общее число частиц N настолько велико, что квантовое число n можно рассматривать как непрерывную переменную. В этом случае общий профиль плотности чисел в ящике действительно однороден.

Число квантовых состояний в диапазоне $n_{1}<n<n_{1}+dn$ является: $$D_{n}(n_{1})\,dn=2\,dn\,.$$

Без ограничения общности энергия нулевой точки выбирается равной нулю, что дает следующий результат:

$$E_{n}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}\implies dE={\frac {\hbar ^{2}\pi ^{2}}{mL^{2}}}n\,dn={\frac {\hbar \pi }{L}}{\sqrt {\frac {2E}{m}}}dn\,.$$

Таким образом, в диапазоне: $$E_{1}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n_{1}^{2}<E<E_{1}+dE\,,$$число квантовых состояний равно: $$D_{n}(n_{1})\,dn=2{\frac {dE}{dE/dn}}={\frac {2}{{\frac {\hbar ^{2}\pi ^{2}}{mL^{2}}}n}}\,dE\equiv D(E_{1})\,dE\,.$$

Здесь степень вырождения равна:

$$D(E)={\frac {2}{dE/dn}}={\frac {2L}{\hbar \pi }}{\sqrt {\frac {m}{2E}}}\,.$$

А плотность состояний равна:

$$g(E)\equiv {\frac {1}{L}}D(E)={\frac {2}{\hbar \pi }}{\sqrt {\frac {m}{2E}}}\,.$$

В современной литературе выше $D(E)$ иногда еще называют «плотностью состояний». Однако, $g(E)$ отличается от $D(E)$ на коэффициент объема системы (который $L$ в этом 1D случае).

На основе следующей формулы:

$$\int _{0}^{E_{\mathrm {F} }}D(E)\,dE=N\,,$$

энергия Ферми в термодинамическом пределе может быть рассчитана как:

$$E_{\mathrm {F} }^{({\text{1D}})}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {N}{2}}\right)^{2}\,.$$

3D однородный газ

Модель атомного ядра, показывающая его как компактный пучок двух типов нуклонов : протонов (красный) и нейтронов (синий). В первом приближении ядро ​​можно рассматривать как состоящее из невзаимодействующих протонов и нейтронных газов.

Трехмерный изотропный и нерелятивистский однородный случай ферми-газа известен как ферми-сфера .

Трехмерная бесконечная квадратная яма (т. е. кубический ящик со стороной L ) имеет потенциальную энергию $$V(x,y,z)={\begin{cases}0,&-{\frac {L}{2}}<x,y,z<{\frac {L}{2}},\\\infty ,&{\text{otherwise.}}\end{cases}}$$

Состояния теперь помечены тремя квантовыми числами n _x , ny _y и n _z . Энергии отдельных частиц равны $$E_{n_{x},n_{y},n_{z}}=E_{0}+{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}\right)\,,$$где n _x , ny _, — положительные n _z целые числа. В этом случае несколько состояний имеют одинаковую энергию (известную как вырожденные уровни энергии ), например $E_{211}=E_{121}=E_{112}$.

Термодинамический предел

Когда ящик содержит N невзаимодействующих фермионов спин- ⁠ 1 / 2 ⁠ интересно вычислить энергию в термодинамическом пределе, где настолько велико, что квантовые числа n _x , ny _N , n _z можно рассматривать как непрерывные переменные.

С вектором $\mathbf {n} =(n_{x},n_{y},n_{z})$, каждое квантовое состояние соответствует точке в «n-пространстве» с энергией $$E_{\mathbf {n} }=E_{0}+{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}|\mathbf {n} |^{2}\,$$

С $|\mathbf {n} |^{2}$обозначающий квадрат обычной евклидовой длины $|\mathbf {n} |={\sqrt {n_{x}^{2}+n_{y}^{2}+n_{z}^{2}}}$.Число состояний с энергией меньше E _F + E ₀ равно числу состояний, лежащих внутри сферы радиуса $|\mathbf {n} _{\mathrm {F} }|$ в области n-пространства, где x _, ny , _{положительны} n z _n . В основном состоянии это число равно числу фермионов в системе:

$$N=2\times {\frac {1}{8}}\times {\frac {4}{3}}\pi n_{\mathrm {F} }^{3}$$

Свободные фермионы, занимающие состояния с наименьшей энергией, образуют сферу в обратном пространстве . Поверхность этой сферы является поверхностью Ферми .

Коэффициент два выражает два спиновых состояния, а коэффициент 1/8 выражает долю сферы, которая находится в области, где все n положительны. $$n_{\mathrm {F} }=\left({\frac {3N}{\pi }}\right)^{1/3}$$Энергия Ферми определяется выражением $$E_{\mathrm {F} }={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n_{\mathrm {F} }^{2}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{2/3}$$

В результате возникает связь между энергией Ферми и числом частиц в объёме (когда L ² заменяется на В. ^2/3 ):

$E_{\mathrm {F} }={\frac {\hbar ^{2}}{2m}}\left({\frac {3\pi ^{2}N}{V}}\right)^{2/3}$

Это также энергия частицы самой высокой энергии (т. $N$-я частица), энергия выше нулевой точки $E_{0}$. $N'$частица имеет энергию $$E_{N'}=E_{0}+{\frac {\hbar ^{2}}{2m}}\left({\frac {3\pi ^{2}N'}{V}}\right)^{2/3}\,=E_{0}+E_{\mathrm {F} }{\big |}_{N'}$$

Полная энергия сферы Ферми $N$ фермионы (которые занимают все $N$ энергетические состояния внутри сферы Ферми) определяется выражением:

$$E_{\rm {T}}=NE_{0}+\int _{0}^{N}E_{\mathrm {F} }{\big |}_{N'}\,dN'=\left({\frac {3}{5}}E_{\mathrm {F} }+E_{0}\right)N$$

Следовательно, средняя энергия на частицу определяется выражением: $$E_{\mathrm {av} }=E_{0}+{\frac {3}{5}}E_{\mathrm {F} }$$

Плотность штатов

Плотность состояний (ПСО) ферми-газа в 3-х измерениях

Для трехмерного однородного ферми-газа с фермионами спина ⁠ 1 / 2 ⁠ , число частиц как функция энергии ${\textstyle N(E)}$ получается заменой энергии Ферми на переменную энергию ${\textstyle (E-E_{0})}$:

$$N(E)={\frac {V}{3\pi ^{2}}}\left[{\frac {2m}{\hbar ^{2}}}(E-E_{0})\right]^{3/2},$$

откуда плотность состояний (количество энергетических состояний на энергию в объеме) $g(E)$ можно получить. Его можно рассчитать, дифференцируя количество частиц по энергии:

$$g(E)={\frac {1}{V}}{\frac {\partial N(E)}{\partial E}}={\frac {1}{2\pi ^{2}}}\left({\frac {2m}{\hbar ^{2}}}\right)^{3/2}{\sqrt {E-E_{0}}}.$$

Этот результат дает альтернативный способ расчета полной энергии ферми-сферы $N$ фермионы (которые занимают все $N$ энергетические состояния внутри сферы Ферми):

$${\begin{aligned}E_{T}&=\int _{0}^{N}E\mathrm {d} N(E)=EN(E){\big |}_{0}^{N}-\int _{E_{0}}^{E_{0}+E_{F}}N(E)\mathrm {d} E\\&=(E_{0}+E_{F})N-\int _{0}^{E_{F}}N(E)\mathrm {d} (E-E_{0})\\&=(E_{0}+E_{F})N-{\frac {2}{5}}E_{F}N(E_{F})=\left(E_{0}+{\frac {3}{5}}E_{\mathrm {F} }\right)N\end{aligned}}$$

Термодинамические величины

Давление вырождения

Кривые зависимости давления от температуры классических и квантовых идеальных газов (ферми-газ, бозе-газ ) в трех измерениях. Отталкивание Паули в фермионах (таких как электроны) придает им дополнительное давление по сравнению с эквивалентным классическим газом, особенно при низкой температуре.

Используя первый закон термодинамики , эту внутреннюю энергию можно выразить как давление, то есть $$P=-{\frac {\partial E_{\rm {T}}}{\partial V}}={\frac {2}{5}}{\frac {N}{V}}E_{\mathrm {F} }={\frac {(3\pi ^{2})^{2/3}\hbar ^{2}}{5m}}\left({\frac {N}{V}}\right)^{5/3},$$где это выражение остается справедливым для температур, много меньших температуры Ферми. Это давление известно как давление вырождения . В этом смысле системы, состоящие из фермионов, также называют вырожденной материей .

Стандартные звезды избегают коллапса, уравновешивая тепловое давление ( плазмы и излучения) и гравитационные силы. В конце жизни звезды, когда тепловые процессы ослабевают, некоторые звезды могут стать белыми карликами, которые противостоят гравитации только за счет давления электронного вырождения . Используя газ Ферми в качестве модели, можно вычислить предел Чандрасекара , то есть максимальную массу, которую может приобрести любая звезда (без значительного термического давления) перед коллапсом в черную дыру или нейтронную звезду. Последняя представляет собой звезду, состоящую в основном из нейтронов, коллапс которой также предотвращается за счет давления нейтронного вырождения.

В случае металлов давление электронного вырождения способствует сжимаемости или объемному модулю материала.

Химический потенциал

Смотрите также: уровень Ферми

Если предположить, что концентрация фермионов не меняется с температурой, то полный химический потенциал ц (уровень Ферми) трехмерного идеального ферми-газа связан с энергией Ферми при нулевой температуре EF _что ( разложением Зоммерфельда при условии, $k_{\rm {B}}T\ll E_{\mathrm {F} }$): $$\mu (T)=E_{0}+E_{\mathrm {F} }\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {k_{\rm {B}}T}{E_{\mathrm {F} }}}\right)^{2}-{\frac {\pi ^{4}}{80}}\left({\frac {k_{\rm {B}}T}{E_{\mathrm {F} }}}\right)^{4}+\cdots \right],$$где Т — температура .

Следовательно, внутренний химический потенциал µ - E 0 _{примерно} равен энергии Ферми при температурах, значительно меньших характеристической температуры Ферми T _F . Эта характерная температура составляет порядка 10 ⁵ K для металла, следовательно, при комнатной температуре (300 К) энергия Ферми и внутренний химический потенциал по существу эквивалентны.

Типичные значения

Металлы

В рамках модели свободных электронов можно считать, что электроны в металле образуют однородный ферми-газ. Плотность числа $N/V$ электронов проводимости в металлах колеблется примерно в пределах 10 ²⁸ и 10 ²⁹ электронов на м ³ , что также является типичной плотностью атомов в обычном твердом веществе. Эта числовая плотность дает энергию Ферми порядка: $$E_{\mathrm {F} }={\frac {\hbar ^{2}}{2m_{e}}}\left(3\pi ^{2}\ 10^{28\ \sim \ 29}\ \mathrm {m^{-3}} \right)^{2/3}\approx 2\ \sim \ 10\ \mathrm {eV} ,$$где m _e — масса покоя электрона . Эта энергия Ферми соответствует температуре Ферми порядка 10 ⁶ Кельвинов, что намного выше температуры поверхности Солнца . Любой металл закипит, не достигнув этой температуры при атмосферном давлении. Таким образом, для любых практических целей в первом приближении металл можно рассматривать как ферми-газ при нулевой температуре (нормальные температуры малы по сравнению с T _F ).

Белые карлики

Звезды, известные как белые карлики, имеют массу, сравнимую с Солнцем , но имеют примерно сотую часть его радиуса. Высокие плотности означают, что электроны больше не связаны с отдельными ядрами и вместо этого образуют вырожденный электронный газ. Плотность электронов у белого карлика порядка 10 ³⁶ электронов/м ³ . Это означает, что их энергия Ферми равна:

$$E_{\mathrm {F} }={\frac {\hbar ^{2}}{2m_{e}}}\left({\frac {3\pi ^{2}(10^{36})}{1\ \mathrm {m^{3}} }}\right)^{2/3}\approx 3\times 10^{5}\ \mathrm {eV} =0.3\ \mathrm {MeV}$$

Ядро

Другой типичный пример — частицы в ядре атома. Радиус ядра примерно равен: $$R=\left(1.25\times 10^{-15}\mathrm {m} \right)\times A^{1/3}$$где А — число нуклонов .

Таким образом, плотность нуклонов в ядре равна:

$$\rho ={\frac {A}{{\frac {4}{3}}\pi R^{3}}}\approx 1.2\times 10^{44}\ \mathrm {m^{-3}}$$

Эту плотность необходимо разделить на два, поскольку энергия Ферми применима только к фермионам одного и того же типа. Наличие нейтронов не влияет на энергию Ферми протонов в ядре, и наоборот.

Энергия Ферми ядра примерно равна: $$E_{\mathrm {F} }={\frac {\hbar ^{2}}{2m_{\rm {p}}}}\left({\frac {3\pi ^{2}(6\times 10^{43})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 3\times 10^{7}\ \mathrm {eV} =30\ \mathrm {MeV} ,$$где m _p — масса протона.

Радиус ядра допускает отклонения от упомянутого выше значения, поэтому типичное значение энергии Ферми обычно дается как 38 МэВ .

Однородный газ произвольных размеров

Плотность штатов

Используя интеграл объема ${\textstyle d}$ размерности, плотность состояний равна:

$$g^{(d)}(E)=g_{s}\int {\frac {\mathrm {d} ^{d}\mathbf {k} }{(2\pi )^{d}}}\delta \left(E-E_{0}-{\frac {\hbar ^{2}|\mathbf {k} |^{2}}{2m}}\right)=g_{s}\ \left({\frac {m}{2\pi \hbar ^{2}}}\right)^{d/2}{\frac {(E-E_{0})^{d/2-1}}{\Gamma (d/2)}}$$

Энергия Ферми получается путем поиска плотности числа частиц: $$\rho ={\frac {N}{V}}=\int _{E_{0}}^{E_{0}+E_{\mathrm {F} }^{(d)}}g^{(d)}(E)\,dE$$

Получить: $$E_{\mathrm {F} }^{(d)}={\frac {2\pi \hbar ^{2}}{m}}\left({\tfrac {1}{g_{s}}}\Gamma \left({\tfrac {d}{2}}+1\right){\frac {N}{V}}\right)^{2/d}$$где ${\textstyle V}$ – соответствующий d -мерный объем, ${\textstyle g_{s}}$ — размерность внутреннего гильбертова пространства. Для случая спин- ⁠ 1 / 2 ⁠ , каждая энергия дважды вырождена, поэтому в этом случае ${\textstyle g_{s}=2}$.

Частный результат получен для $d=2$, где плотность состояний становится постоянной (не зависит от энергии): $$g^{(2\mathrm {D} )}(E)={\frac {g_{s}}{2}}{\frac {m}{\pi \hbar ^{2}}}.$$

Ферми-газ в гармонической ловушке

Основная статья: Газ в гармонической ловушке

Потенциал гармонической ловушки :

$$V(x,y,z)={\frac {1}{2}}m\omega _{x}^{2}x^{2}+{\frac {1}{2}}m\omega _{y}^{2}y^{2}+{\frac {1}{2}}m\omega _{z}^{2}z^{2}$$

это модельная система со множеством приложений в современной физике. Плотность состояний (или, точнее, степень вырождения) для данного вида спина равна:

$$g(E)={\frac {E^{2}}{2(\hbar \omega _{\text{ho}})^{3}}}\,,$$

где $\omega _{\text{ho}}={\sqrt[{3}]{\omega _{x}\omega _{y}\omega _{z}}}$ – частота гармонических колебаний.

Энергия Ферми для данного вида спина равна:

$$E_{\rm {F}}=(6N)^{1/3}\hbar \omega _{\text{ho}}\,.$$

Соответствующие величины Ферми

В современной литературе часто встречаются несколько полезных величин, связанных с энергией Ферми.

Температура Ферми определяется как ${\textstyle T_{\mathrm {F} }={\frac {E_{\mathrm {F} }}{k_{\rm {B}}}}}$, где $k_{\rm {B}}$ — постоянная Больцмана . Температуру Ферми можно рассматривать как температуру, при которой тепловые эффекты сравнимы с квантовыми эффектами, связанными со статистикой Ферми. Температура Ферми металла на пару порядков выше комнатной температуры. Другими величинами, определяемыми в этом контексте, являются импульс Ферми. ${\textstyle p_{\mathrm {F} }={\sqrt {2mE_{\mathrm {F} }}}}$и скорость Ферми ${\textstyle v_{\mathrm {F} }={\frac {p_{\mathrm {F} }}{m}}}$, которые представляют собой импульс и групповую скорость соответственно фермиона на поверхности Ферми . Импульс Ферми также можно описать как $p_{\mathrm {F} }=\hbar k_{\mathrm {F} }$, где $k_{\mathrm {F} }$ — радиус сферы Ферми и называется волновым вектором Ферми .

Обратите внимание, что эти величины не определены четко в случаях, когда поверхность Ферми несферическая.

Обработка при конечной температуре

Большой канонический ансамбль

Большинство приведенных выше расчетов точны при нулевой температуре, но остаются хорошими приближениями для температур ниже температуры Ферми. Для остальных термодинамических переменных необходимо написать термодинамический потенциал . Для ансамбля идентичных фермионов лучший способ получить потенциал — это использовать большой канонический ансамбль с фиксированной температурой, объемом и химическим потенциалом μ . Причина кроется в принципе исключения Паули, поскольку числа заполнения каждого квантового состояния задаются либо 1, либо 0 (либо есть электрон, занимающий это состояние, либо нет), поэтому (большая) статистическая сумма ${\mathcal {Z}}$ можно записать как

${\mathcal {Z}}(T,V,\mu )=\sum _{\{q\}}e^{-\beta (E_{q}-\mu N_{q})}=\prod _{q}\sum _{n_{q}=0}^{1}e^{-\beta (\varepsilon _{q}-\mu )n_{q}}=\prod _{q}\left(1+e^{-\beta (\varepsilon _{q}-\mu )}\right),$

где $\beta ^{-1}=k_{\rm {B}}T$, $\{q\}$ индексирует ансамбли всех возможных микросостояний, которые дают одинаковую полную энергию ${\textstyle E_{q}=\sum _{q}\varepsilon _{q}n_{q}}$ и количество частиц ${\textstyle N_{q}=\sum _{q}n_{q}}$, ${\textstyle \varepsilon _{q}}$ - это одночастичная энергия состояния ${\textstyle q}$ (он учитывается дважды, если энергия состояния вырождена) и ${\textstyle n_{q}=0,1}$, его заполняемость. Таким образом, великий потенциал записывается как

$\Omega (T,V,\mu )=-k_{\rm {B}}T\ln \left({\mathcal {Z}}\right)=-k_{\rm {B}}T\sum _{q}\ln \left(1+e^{\beta (\mu -\varepsilon _{q})}\right).$

Тот же результат можно получить в каноническом и микроканоническом ансамбле , поскольку результат каждого ансамбля должен давать одно и то же значение в термодинамическом пределе. ${\textstyle (N/V\rightarrow \infty )}$. Здесь рекомендуется использовать большой канонический ансамбль, поскольку он позволяет избежать использования комбинаторики и факториалов .

Как обсуждалось в предыдущих разделах, в макроскопическом пределе мы можем использовать непрерывное приближение ( приближение Томаса – Ферми ), чтобы преобразовать эту сумму в интеграл: $$\Omega (T,V,\mu )=-k_{\rm {B}}T\int _{-\infty }^{\infty }D(\varepsilon )\ln \left(1+e^{\beta (\mu -\varepsilon )}\right)\,d\varepsilon$$где D ( ε ) — полная плотность состояний.

Связь с распределением Ферми – Дирака

Большой потенциал связан с числом частиц при конечной температуре следующим образом $$N=-\left({\frac {\partial \Omega }{\partial \mu }}\right)_{T,V}=\int _{-\infty }^{\infty }D(\varepsilon ){\mathcal {f}}\left({\frac {\varepsilon -\mu }{k_{\rm {B}}T}}\right)\,\mathrm {d} \varepsilon$$где производная берется при фиксированных температуре и объеме и имеет вид $${\mathcal {f}}(x)={\frac {1}{e^{x}+1}}$$также известное как распределение Ферми-Дирака .

Аналогично, полная внутренняя энергия равна $$U=\Omega -T\left({\frac {\partial \Omega }{\partial T}}\right)_{V,\mu }-\mu \left({\frac {\partial \Omega }{\partial \mu }}\right)_{T,V}=\int _{-\infty }^{\infty }D(\varepsilon ){\mathcal {f}}\!\left({\frac {\varepsilon -\mu }{k_{\rm {B}}T}}\right)\varepsilon \,d\varepsilon .$$

Точное решение для степенной плотности состояний

Многие интересующие нас системы имеют общую плотность состояний степенного вида: $$D(\varepsilon )=Vg(\varepsilon )={\frac {Vg_{0}}{\Gamma (\alpha )}}(\varepsilon -\varepsilon _{0})^{\alpha -1},\qquad \varepsilon \geq \varepsilon _{0}$$для некоторых значений g ₀ , α , ε ₀ . Результаты предыдущих разделов обобщаются на d -мерности, давая степенной закон:

• α = d /2 для нерелятивистских частиц в d -мерном ящике,
• α = d для нерелятивистских частиц в d -мерной гармонической потенциальной яме,
• α = d для гиперрелятивистских частиц в d -мерном ящике.

Для такой степенной плотности состояний большой потенциальный интеграл равен: $$\Omega (T,V,\mu )=-Vg_{0}(k_{\rm {B}}T)^{\alpha +1}F_{\alpha }\left({\frac {\mu -\varepsilon _{0}}{k_{\rm {B}}T}}\right),$$где $F_{\alpha }(x)$ — полный интеграл Ферми–Дирака (связанный с полилогарифмом ). Из этого грандиозного потенциала и его производных можно извлечь все интересующие термодинамические величины.

Расширения модели

Релятивистский ферми-газ

Отношения радиус-масса для модельного белого карлика, релятивистское соотношение против нерелятивистского. обозначается Предел Чандрасекара как M _Ch .

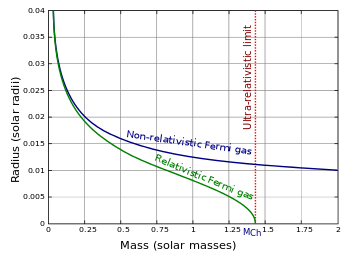
В статье рассмотрен только случай, когда частицы имеют параболическую связь между энергией и импульсом, как это имеет место в нерелятивистской механике. Для частиц с энергией, близкой к их соответствующей массе покоя уравнения специальной теории относительности , применимы . Где энергия одной частицы определяется выражением: $$E={\sqrt {(pc)^{2}+(mc^{2})^{2}}}.$$

Для этой системы энергия Ферми определяется выражением: $$E_{\mathrm {F} }={\sqrt {(p_{\mathrm {F} }c)^{2}+(mc^{2})^{2}}}-mc^{2}\approx p_{\mathrm {F} }c,$$где $\approx$ равенство справедливо только в ультрарелятивистском пределе , и $$p_{\mathrm {F} }=\hbar \left({\frac {1}{g_{s}}}6\pi ^{2}{\frac {N}{V}}\right)^{1/3}.$$

Релятивистская модель ферми-газа используется также для описания массивных белых карликов, близких к пределу Чандрасекара . Для ультрарелятивистского случая давление вырождения пропорционально $(N/V)^{4/3}$.

Ферми-жидкость

В 1956 году Лев Ландау разработал теорию ферми-жидкости , в которой рассмотрел случай ферми-жидкости, т. е. системы с отталкивающими, не обязательно малыми, взаимодействиями между фермионами. Теория показывает, что термодинамические свойства идеального ферми-газа и ферми-жидкости не сильно различаются. Можно показать, что ферми-жидкость эквивалентна ферми-газу, состоящему из коллективных возбуждений или квазичастиц , каждая из которых имеет различную эффективную массу и магнитный момент .

См. также

• Бозе-газ
• Фермионный конденсат
• Газ в коробке
• Желе
• Двумерный электронный газ

Дальнейшее чтение

• Нил В. Эшкрофт и Н. Дэвид Мермин , Физика твердого тела (Harcourt: Орландо, 1976).
• Чарльз Киттель , Введение в физику твердого тела , 1-е изд. 1953 - 8-е изд. 2005, ISBN   0-471-41526-X