Шестигранные 8-симплексы

Шестигранный 8-симплекс
Ортогональная проекция на плоскость Кокстера A8
Тип	однородный 8-многогранник
Символ Шлефли	т 0,6 {3.3.3.3.3.3.3}
Диаграммы Кокстера-Динкина
7-гранный
6-гранный
5-гранный
4-ликий
Клетки
Лица
Края	2268
Вершины	252
Вершинная фигура
Группы Кокстера	А 8 , [3 7 ], заказ 362880
Характеристики	выпуклый

В восьмимерной геометрии шестигранный 8-симплекс представляет собой однородный 8-многогранник , являющийся гексикацией (усечением 6-го порядка) правильного 8-симплекса .

Декартовы координаты вершин шестигранного 8-симплекса проще всего расположить в 9-мерном пространстве как перестановки (0,0,0,1,1,1,1,1,2). Эта конструкция основана на гранях шестигранного 9-ортоплекса .

Изображения

орфографические проекции

АК Коксетера Самолет	А 8	A 7	А 6	AА5
График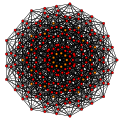
Двугранная симметрия	[9]	[8]	[7]	[6]
А.К.Коксетера ​ План	A 4	AА3	AА2
График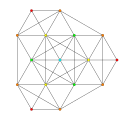
Двугранная симметрия	[5]	[4]	[3]

Связанные многогранники

Этот многогранник является одним из 135 однородных 8-многогранников с симметрией A ₈ .

Ссылки

• ХСМ Коксетер :
  • HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
  • Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1]
    • (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
    • (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
    • (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
• Нормана Джонсона Равномерные многогранники , Рукопись (1991)
  • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии
• Клитцинг, Ричард. «8D однородные многогранники (polyzetta) x3o3o3o3o3o3x3o» .

Внешние ссылки

• Многогранники различных размерностей
• Многомерный глоссарий