Обучение без присмотра

Обучение без учителя — это основа машинного обучения , в которой, в отличие от обучения с учителем , алгоритмы изучают закономерности исключительно на основе немаркированных данных. ^[1] Другие структуры в спектре надзора включают слабый или полунадзор , когда небольшая часть данных помечается, и самоконтроль . Некоторые исследователи считают обучение с самоконтролем формой обучения без учителя. ^[2]

Концептуально обучение без учителя делится на аспекты данных, обучения, алгоритмов и последующих приложений. Как правило, набор данных собирается дешево «в дикой природе», например, массивный текстовый корпус, полученный путем сканирования веб-страниц , с лишь незначительной фильтрацией (например, Common Crawl ). Это выгодно отличается от контролируемого обучения, при котором набор данных (например, ImageNet1000 ) обычно создается вручную, что намного дороже.

Существовали алгоритмы, разработанные специально для обучения без учителя, такие как алгоритмы кластеризации, такие как k-means , уменьшения размерности методы , такие как анализ главных компонентов (PCA) , машинное обучение Больцмана и автокодировщики . После появления глубокого обучения большая часть крупномасштабного обучения без учителя осуществлялась путем обучения архитектур нейронных сетей общего назначения методом градиентного спуска , адаптированных к выполнению обучения без учителя путем разработки соответствующей процедуры обучения.

Иногда обученную модель можно использовать как есть, но чаще всего ее модифицируют для последующих приложений. Например, метод генеративного предварительного обучения обучает модель генерированию набора текстовых данных перед его точной настройкой для других приложений, таких как классификация текста. ^[3]^[4] Еще один пример: автоэнкодеры обучаются хорошим функциям , которые затем можно использовать в качестве модуля для других моделей, например, в модели скрытой диффузии .

Задачи

Тенденция к использованию в задаче контролируемых и неконтролируемых методов. Названия задач, выходящие за границы круга, созданы намеренно. Это показывает, что классическое разделение творческих задач (слева) с использованием неконтролируемых методов размыто в современных схемах обучения.

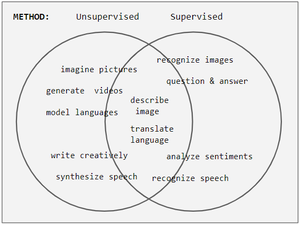
Задачи часто делятся на дискриминационные (распознавание) и порождающие (воображение). Часто, но не всегда, в распознавательных задачах используются контролируемые методы, а в генеративных задачах — неконтролируемые (см. диаграмму Венна ); однако разделение очень размыто. Например, распознавание объектов способствует обучению с учителем, но обучение без учителя также может группировать объекты в группы. Более того, по мере продвижения вперед в некоторых задачах используются оба метода, а в некоторых задачах меняется один на другой. Например, распознавание изображений началось с жесткого контроля, но стало гибридным из-за использования неконтролируемого предварительного обучения, а затем снова перешло к контролю с появлением отсева , ReLU и адаптивных скоростей обучения .

Типичная генеративная задача выглядит следующим образом. На каждом этапе из набора данных выбирается точка данных, часть данных удаляется, и модель должна вывести удаленную часть. Это особенно очевидно для автоэнкодеров с шумоподавлением и BERT .

Архитектуры нейронных сетей

Обучение

На этапе обучения неконтролируемая сеть пытается имитировать предоставленные ей данные и использует ошибку в имитируемых выходных данных, чтобы исправить себя (т. е. исправить свои веса и смещения). Иногда ошибка выражается как низкая вероятность возникновения ошибочного вывода или как нестабильное состояние с высокой энергией в сети.

В отличие от доминирующего использования обратного распространения ошибки в методах с учителем , в обучении без учителя также используются другие методы, в том числе: правило обучения Хопфилда, правило обучения Больцмана, контрастное расхождение , бодрствование во сне , вариационный вывод , максимальное правдоподобие , максимум апостериори , выборка Гиббса и ошибки реконструкции с обратным распространением ошибки. или скрытые репараметризации состояния. Более подробную информацию смотрите в таблице ниже.

Энергия

Энергетическая функция — это макроскопическая мера состояния активации сети. В машинах Больцмана она играет роль функции стоимости. Эта аналогия с физикой навеяна анализом Людвигом Больцманом макроскопической энергии газа на основе микроскопических вероятностей движения частиц. $p\propto e^{-E/kT}$ , где k — постоянная Больцмана, а T — температура. В сети RBM соотношение $p=e^{-E}/Z$ , ^[5] где $p$ и $E$ различаться по каждому возможному шаблону активации и $\textstyle {Z=\sum _{\scriptscriptstyle {\text{All Patterns}}}e^{-E({\text{pattern}})}}$ . Если быть более точным, $p(a)=e^{-E(a)}/Z$ , где $a$ представляет собой паттерн активации всех нейронов (видимых и скрытых). Следовательно, некоторые ранние нейронные сети носят название «Машина Больцмана». Павел Смоленский звонит $-E\,$ Гармония . Сеть ищет низкую энергию и высокую Гармонию.

Сети

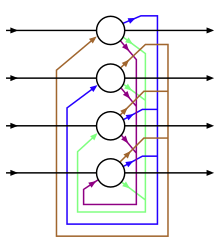
В этой таблице приведены схемы подключения различных неконтролируемых сетей, подробности о которых будут приведены в разделе «Сравнение сетей». Круги — это нейроны, а ребра между ними — веса связей. По мере изменения конструкции сети функции добавляются, чтобы обеспечить новые возможности, или удаляются, чтобы ускорить обучение. Например, нейроны меняются между детерминированными (Хопфилд) и стохастическими (Больцманн), чтобы обеспечить надежный вывод, веса удаляются внутри слоя (RBM), чтобы ускорить обучение, или соединениям позволяют стать асимметричными (Гельмгольц).

Хопфилд	Больцман	УОР	Сложенный Больцман
Сеть на основе магнитных доменов в железе с одним самосвязным слоем. Его можно использовать в качестве адресуемой памяти по содержимому.	Сеть разделена на два слоя (скрытый и видимый), но при этом используются симметричные двусторонние веса. Согласно термодинамике Больцмана, отдельные вероятности порождают макроскопические энергии.	Ограниченная машина Больцмана. Это машина Больцмана, в которой боковые связи внутри слоя запрещены, чтобы облегчить анализ.	Эта сеть имеет несколько RBM для кодирования иерархии скрытых функций. После обучения одного RBM добавляется еще один синий скрытый слой (см. RBM слева), а два верхних слоя обучаются как красный и синий RBM. Таким образом, средние уровни RBM действуют как скрытые или видимые, в зависимости от фазы обучения, на которой они находятся.

Гельмгольц	Автоэнкодер	НОГИ
Вместо двунаправленного симметричного соединения многоуровневых машин Больцмана у нас есть отдельные односторонние соединения, образующие петлю. Он выполняет как генерацию, так и дискриминацию.	Сеть прямой связи, целью которой является поиск хорошего представления среднего уровня своего входного мира. Эта сеть является детерминированной, поэтому она не так надежна, как ее преемница VAE.	Применяет вариационный вывод к автоэнкодеру. Средний уровень представляет собой набор средних и дисперсий для гауссовских распределений. Стохастическая природа обеспечивает более сильное воображение, чем детерминированный автокодировщик.

Из сетей, носящих имена людей, только Хопфилд работал напрямую с нейронными сетями. Больцман и Гельмгольц появились раньше искусственных нейронных сетей, но их работы в области физики и физиологии вдохновили на использование аналитических методов.

История

1974	Магнитная модель Изинга, предложенная У. А. Литтлом [ де ] для познания
1980	На Фукусиме внедряется неокогнитрон , который позже назовут сверточной нейронной сетью . Чаще всего он используется в SL, но здесь заслуживает упоминания.
1982	Вариант сети Хопфилда Изинга, описанный как CAM Джоном Хопфилдом и классификаторы.
1983	Вариант машины Больцмана Изинга с вероятностными нейронами, описанный Хинтоном и Сейновски после работы Шерингтона и Киркпатрика 1975 года.
1986	Пол Смоленский публикует «Теорию гармонии», которая представляет собой RBM с практически той же энергетической функцией Больцмана. Смоленский не дал схемы практической подготовки. Хинтон сделал это в середине 2000-х.
1995	Шмидтубер представляет нейрон LSTM для языков.
1995	Dayan & Hinton представляет машину Гельмгольца
2013	Кингма, Резенде и компания. представила вариационные автоэнкодеры как байесовскую графическую вероятностную сеть с нейронными сетями в качестве компонентов.

Конкретные сети

Здесь мы выделим некоторые характеристики избранных сетей. Подробности о каждом из них приведены в сравнительной таблице ниже.

Сеть Хопфилда: Ферромагнетизм вдохновил сети Хопфилда. Нейрон соответствует железному домену с бинарными магнитными моментами Up и Down, а нейронные связи соответствуют влиянию домена друг на друга. Симметричные связи позволяют создать глобальную энергетическую формулу. Во время вывода сеть обновляет каждое состояние, используя стандартную функцию шага активации. Симметричные веса и правильные энергетические функции гарантируют сходимость к стабильному шаблону активации. Асимметричные веса трудно анализировать. Сети Хопфилда используются в качестве адресуемой памяти (CAM).
Машина Больцмана: Это стохастические сети Хопфилда. Значение их состояния выбирается из этого PDF-файла следующим образом: предположим, что бинарный нейрон срабатывает с вероятностью Бернулли p(1) = 1/3 и отдыхает с p(0) = 2/3. Из него берут выборку, беря равномерно распределенное случайное число y и подставляя его в инвертированную кумулятивную функцию распределения , которая в данном случае является ступенчатой функцией с порогом 2/3. Обратная функция = { 0, если x <= 2/3, 1, если x > 2/3 }.
Сигмовидная сеть убеждений: Эта сеть, представленная Рэдфордом Нилом в 1992 году, применяет идеи вероятностных графических моделей к нейронным сетям. Ключевое отличие состоит в том, что узлы в графических моделях имеют заранее заданные значения, тогда как функции нейронов сети убеждений определяются после обучения. Сеть представляет собой разреженный ориентированный ациклический граф, состоящий из бинарных стохастических нейронов. Правило обучения основано на максимальном правдоподобии для p(X): Δw _ij $\propto$ s _j * (s _i - p _i ), где p _i = 1 / ( 1 + e ^{взвешенные входы в нейрон i} ). s _j являются активациями из несмещенной выборки апостериорного распределения, и это проблематично из-за проблемы объяснения, поднятой Джудой Перлом. Вариационные байесовские методы используют суррогатный апостериор и явно игнорируют эту сложность.
Сеть глубоких убеждений: Эта сеть, представленная Хинтоном, представляет собой гибрид RBM и сигмовидной сети убеждений. Два верхних уровня представляют собой RBM, а второй уровень, расположенный ниже, образует сигмовидную сеть убеждений. Его обучают методом составного RBM , а затем отбрасывают веса распознавания ниже верхнего RBM. По состоянию на 2009 год оптимальной глубиной кажется 3-4 слоя. ^[6]
Машина Гельмгольца: Это ранние источники вдохновения для вариационных автоэнкодеров. Его две сети объединены в одну: прямые веса управляют распознаванием, а обратные веса реализуют воображение. Возможно, это первая сеть, которая делает и то, и другое. Гельмгольц не занимался машинным обучением, но он вдохновил идею «машины статистического вывода, функция которой состоит в том, чтобы определить вероятные причины сенсорной информации». ^[7] стохастический бинарный нейрон выдает вероятность того, что его состояние равно 0 или 1. Входные данные обычно не считаются слоем, но в режиме генерации машины Гельмгольца уровень данных получает входные данные от среднего уровня и имеет для этой цели отдельные веса, поэтому это считается слоем. Следовательно, эта сеть имеет 3 слоя.
Вариационный автоэнкодер: Они вдохновлены машинами Гельмгольца и сочетают в себе сеть вероятностей с нейронными сетями. Автоэнкодер — это трехуровневая сеть CAM, где средний уровень должен представлять собой некоторое внутреннее представление входных шаблонов. Нейронная сеть кодера представляет собой распределение вероятностей q _φ (z при заданном x), а сеть декодера — это p _θ (x при заданном z). Веса называются фи и тета, а не W и V, как у Гельмгольца — косметическое отличие. Эти две сети здесь можно полностью соединить или использовать другую схему NN.

Сравнение сетей

	Хопфилд	Больцман	УОР	Сложенный УОР	Гельмгольц	Автоэнкодер	НОГИ
Использование и примечания	CAM, задача коммивояжера	САМ. Свобода связей затрудняет анализ этой сети.	распознавание образов. используется в цифрах и речи MNIST.	узнавание и воображение. обучены с помощью предварительной подготовки без присмотра и/или контролируемой точной настройки.	воображение, мимикрия	язык: творческое письмо, перевод. зрение: улучшение размытых изображений	генерировать реалистичные данные
Нейрон	детерминированное бинарное состояние. Активация = { 0 (или -1), если x отрицательное значение, 1 в противном случае }	стохастический бинарный нейрон Хопфилда	← то же самое. (распространено на реальную стоимость середины 2000-х годов)	← то же самое	← то же самое	язык: LSTM. зрение: локальные рецептивные поля. обычно активация relu имеет действительное значение.	Нейроны среднего слоя кодируют средние значения и отклонения для гауссиан. В режиме выполнения (вывод) выходные данные среднего слоя представляют собой выборочные значения гауссиан.
Соединения	1-слойный с симметричными грузами. Никаких самоподключений.	2-слойные. 1-скрытый и 1-видимый. симметричные веса.	← то же самое. нет боковых связей внутри слоя.	верхний слой ненаправленный, симметричный. остальные слои двухсторонние, асимметричные.	3 слоя: асимметричные веса. 2 сети объединены в 1.	3-слойные. Входные данные считаются слоем, даже если они не имеют входящих весов. рекуррентные слои для НЛП. извилины с прямой связью для зрения. вход и выход имеют одинаковое количество нейронов.	3 уровня: вход, кодер, декодер сэмплера распределения. сэмплер не считается слоем
Выводы и энергия	Энергия определяется вероятностной мерой Гиббса: $E=-{\frac {1}{2}}\sum _{i,j}{w_{ij}{s_{i}}{s_{j}}}+\sum _{i}{\theta _{i}}{s_{i}}$	← то же самое	← то же самое		минимизировать расхождение KL	вывод является только прямой связью. предыдущие сети UL работали вперед И назад	ошибка минимизации = ошибка реконструкции - KLD
Обучение	Δw _ij = s _i *s _j , для +1/-1 нейрона	Δw _ij = e*(p _ij - p' _ij ). Это получено в результате минимизации KLD. e = скорость обучения, p' = прогнозируемое и p = фактическое распределение.	Δw _ij = e*( < v _i h _j > _данные - < v _i h _j > _{равновесие} ). Это форма контрастного расхождения с выборкой Гиббса. «<>» — ожидания.	← похожее. тренируйте по одному слою за раз. приблизительное равновесное состояние при 3-сегментном проходе. нет обратного распространения.	двухфазная тренировка бодрствования и сна	обратное распространение ошибки реконструкции	перепараметризировать скрытое состояние для обратного распространения
Сила	напоминает физические системы, поэтому наследует их уравнения	← то же самое. скрытые нейроны действуют как внутреннее представление внешнего мира	более быстрая и практичная схема обучения, чем на машинах Больцмана	тренируется быстро. дает иерархический уровень функций	умеренно анатомический. поддается анализу с помощью теории информации и статистической механики
Слабость		трудно тренироваться из-за боковых связей	равновесие требует слишком много итераций	Целочисленные и действительные нейроны более сложны.

Хеббианское обучение, ART, SOM

Классическим примером обучения без учителя при изучении нейронных сетей является принцип Дональда Хебба , то есть нейроны, которые срабатывают вместе, соединяются вместе. ^[8] При обучении Хебба связь усиливается независимо от ошибки, но является исключительно функцией совпадения потенциалов действия между двумя нейронами. ^[9] Аналогичная версия, которая изменяет синаптические веса, учитывает время между потенциалами действия ( пластичность, зависящая от времени спайка , или STDP). Было высказано предположение, что хеббианское обучение лежит в основе ряда когнитивных функций, таких как распознавание образов и экспериментальное обучение.

Среди нейронных сетей моделей самоорганизующаяся карта (SOM) и теория адаптивного резонанса в алгоритмах обучения без учителя обычно используются (ART). SOM — это топографическая организация, в которой близлежащие места на карте представляют собой входные данные со схожими свойствами. Модель ART позволяет изменять количество кластеров в зависимости от размера проблемы и позволяет пользователю контролировать степень сходства между членами одних и тех же кластеров с помощью определяемой пользователем константы, называемой параметром бдительности. Сети ART используются для многих задач распознавания образов, таких как автоматическое распознавание целей и обработка сейсмических сигналов. ^[10]

Вероятностные методы

Двумя основными методами, используемыми в обучении без учителя, являются анализ главных компонентов и кластерный анализ . Кластерный анализ используется при обучении без учителя для группировки или сегментирования наборов данных с общими атрибутами для экстраполяции алгоритмических связей. ^[11] Кластерный анализ — это отрасль машинного обучения , которая группирует данные, которые не были помечены , классифицированы или категоризированы. Вместо реагирования на обратную связь кластерный анализ выявляет общие черты в данных и реагирует на основе наличия или отсутствия таких общих черт в каждой новой части данных. Этот подход помогает обнаружить аномальные точки данных, которые не вписываются ни в одну группу.

Основное применение обучения без учителя находится в области оценки плотности в статистике . ^[12] хотя обучение без учителя охватывает множество других областей, связанных с обобщением и объяснением особенностей данных. Его можно противопоставить обучению с учителем, сказав, что обучение с учителем направлено на вывод условного распределения вероятностей, обусловленного меткой входных данных; Обучение без учителя направлено на получение априорного распределения вероятностей.

Подходы

Некоторые из наиболее распространенных алгоритмов, используемых в обучении без учителя, включают: (1) Кластеризация, (2) Обнаружение аномалий, (3) Подходы к обучению моделей со скрытыми переменными. Каждый подход использует несколько методов, а именно:

К методам кластеризации относятся: иерархическая кластеризация , ^[13] k-значит , ^[14] смешанные модели , кластеризация на основе моделей , DBSCAN и OPTICS алгоритм
обнаружения аномалий К методам относятся: локальный коэффициент выбросов и изоляционный лес.
Подходы к изучению моделей со скрытыми переменными, такие как алгоритм ожидания-максимизации (EM), метод моментов и методы слепого разделения сигналов ( анализ главных компонентов , анализ независимых компонентов , факторизация неотрицательной матрицы , разложение по сингулярным значениям )

Метод моментов

Одним из статистических подходов к обучению без учителя является метод моментов . В методе моментов неизвестные параметры (интересующие) в модели связаны с моментами одной или нескольких случайных величин, и, таким образом, эти неизвестные параметры могут быть оценены с учетом моментов. Моменты обычно оцениваются по выборкам эмпирическим путем. Базовыми моментами являются моменты первого и второго порядка. Для случайного вектора момент первого порядка — это средний вектор, а момент второго порядка — ковариационная матрица (когда среднее значение равно нулю). Моменты более высокого порядка обычно представляются с помощью тензоров , которые представляют собой обобщение матриц до более высоких порядков в виде многомерных массивов.

В частности, показана эффективность метода моментов при изучении параметров моделей со скрытыми переменными . Модели со скрытыми переменными — это статистические модели, в которых помимо наблюдаемых переменных существует также набор скрытых переменных, которые не наблюдаются. Весьма практичным примером моделей латентных переменных в машинном обучении является тематическое моделирование , которое представляет собой статистическую модель для генерации слов (наблюдаемых переменных) в документе на основе темы (латентной переменной) документа. При тематическом моделировании слова в документе генерируются в соответствии с различными статистическими параметрами при изменении темы документа. Показано, что метод моментов (методы тензорной декомпозиции) последовательно восстанавливают параметры большого класса моделей со скрытыми переменными при некоторых предположениях. ^[15]

Алгоритм ожидания-максимизации (EM) также является одним из наиболее практичных методов изучения моделей со скрытыми переменными. Однако он может застрять в локальных оптимумах, и нет гарантии, что алгоритм сходится к истинным неизвестным параметрам модели. Напротив, для метода моментов глобальная сходимость гарантируется при некоторых условиях.

См. также

Ссылки

^ Ву, Вэй. «Обучение без учителя» (PDF) . Архивировано (PDF) из оригинала 14 апреля 2024 года . Проверено 26 апреля 2024 г.
^ Чжаоюй; Чжан, Цзин, Цзе (2021). Хоу , Ван , Чжэньюй ; Лю, Сяо, Фаньцзинь ; 1–1 дои : 10.1109/ TKDE.2021.3090866 ISSN 1041-4347 .
^ Рэдфорд, Алек; Нарасимхан, Картик; Салиманс, Тим; Суцкевер, Илья (11 июня 2018 г.). «Улучшение понимания языка посредством генеративной предварительной подготовки» (PDF) . ОпенАИ . п. 12. Архивировано (PDF) из оригинала 26 января 2021 года . Проверено 23 января 2021 г.
^ Ли, Чжохань; Уоллес, Эрик; Шен, Шэн; Лин, Кевин; Кейцер, Курт; Кляйн, Дэн; Гонсалес, Джоуи (21 ноября 2020 г.). «Обучайтесь больше, затем сжимайте: переосмысление размера модели для эффективного обучения и вывода трансформаторов» . Материалы 37-й Международной конференции по машинному обучению . ПМЛР: 5958–5968.
^ Хинтон, Г. (2012). «Практическое руководство по обучению ограниченных машин Больцмана» (PDF) . Нейронные сети: хитрости . Конспекты лекций по информатике. Том. 7700. Спрингер. стр. 599–619. дои : 10.1007/978-3-642-35289-8_32 . ISBN 978-3-642-35289-8 . Архивировано (PDF) из оригинала 3 сентября 2022 г. Проверено 3 ноября 2022 г.
^ Хинтон, Джеффри (сентябрь 2009 г.). «Сети глубокой веры» (видео). Архивировано из оригинала 8 марта 2022 г. Проверено 27 марта 2022 г.
^ Питер, Даян ; Хинтон, Джеффри Э .; Нил, Рэдфорд М .; Земель, Ричард С. (1995). «Машина Гельмгольца». Нейронные вычисления . 7 (5): 889–904. дои : 10.1162/neco.1995.7.5.889 . hdl : 21.11116/0000-0002-D6D3-E . ПМИД 7584891 . S2CID 1890561 .
^ Буманн, Дж.; Кунель, Х. (1992). «Неконтролируемая и контролируемая кластеризация данных с помощью конкурентных нейронных сетей». [Труды 1992 г.] Международная совместная конференция IJCNN по нейронным сетям . Том. 4. ИИЭР. стр. 796–801. дои : 10.1109/ijcnn.1992.227220 . ISBN 0780305590 . S2CID 62651220 .
^ Комесанья-Кампос, Альберто; Буза-Родригес, Хосе Бенито (июнь 2016 г.). «Применение Хеббианского обучения при принятии решений в процессе проектирования». Журнал интеллектуального производства . 27 (3): 487–506. дои : 10.1007/s10845-014-0881-z . ISSN 0956-5515 . S2CID 207171436 .
^ Карпентер, Джорджия, и Гроссберг, С. (1988). «ИСКУССТВО адаптивного распознавания образов с помощью самоорганизующейся нейронной сети» (PDF) . Компьютер . 21 (3): 77–88. дои : 10.1109/2.33 . S2CID 14625094 . Архивировано из оригинала (PDF) 16 мая 2018 г. Проверено 16 сентября 2013 г.
^ Роман, Виктор (21 апреля 2019 г.). «Машинное обучение без учителя: кластерный анализ» . Середина . Архивировано из оригинала 21 августа 2020 г. Проверено 1 октября 2019 г.
^ Джордан, Майкл И.; Бишоп, Кристофер М. (2004). «7. Интеллектуальные системы §Нейронные сети». В Такере, Аллен Б. (ред.). Справочник по информатике (2-е изд.). Чепмен и Холл/CRC Press. дои : 10.1201/9780203494455 . ISBN 1-58488-360-Х . Архивировано из оригинала 3 ноября 2022 г. Проверено 3 ноября 2022 г.
^ Хасти, Тибширани и Фридман, 2009 , стр. 485–586.
^ Гарбаде, доктор Майкл Дж. (12 сентября 2018 г.). «Понимание кластеризации K-средних в машинном обучении» . Середина . Архивировано из оригинала 28 мая 2019 г. Проверено 31 октября 2019 г.
^ Анандкумар, Анимашри; Ге, Ронг; Сюй, Дэниел; Какаде, Шам; Тельгарский, Матус (2014). «Тензорные разложения для изучения моделей со скрытыми переменными» (PDF) . Журнал исследований машинного обучения . 15 : 2773–2832. arXiv : 1210.7559 . Бибкод : 2012arXiv1210.7559A . Архивировано (PDF) из оригинала 20 марта 2015 г. Проверено 10 апреля 2015 г.

Дальнейшее чтение

Буске, О.; фон Люксбург, США ; Раетч, Г., ред. (2004). Продвинутые лекции по машинному обучению . Спрингер. ISBN 978-3540231226 .
Дуда, Ричард О .; Харт, Питер Э .; Сторк, Дэвид Г. (2001). «Обучение без учителя и кластеризация». Классификация узоров (2-е изд.). Уайли. ISBN 0-471-05669-3 .
Хасти, Тревор ; Тибширани, Роберт ; Фридман, Джером (2009). «Обучение без учителя» . Элементы статистического обучения: интеллектуальный анализ данных, логические выводы и прогнозирование . Спрингер. стр. 485–586. дои : 10.1007/978-0-387-84858-7_14 . ISBN 978-0-387-84857-0 . Архивировано из оригинала 3 ноября 2022 г. Проверено 3 ноября 2022 г.
Хинтон, Джеффри ; Сейновский, Терренс Дж. , ред. (1999). Обучение без учителя: основы нейронных вычислений . МТИ Пресс . ISBN 0-262-58168-Х .

[WeiWu-1] Ву, Вэй. «Обучение без учителя» (PDF) . Архивировано (PDF) из оригинала 14 апреля 2024 года . Проверено 26 апреля 2024 г.

[2] Чжаоюй; Чжан, Цзин, Цзе (2021). Хоу , Ван , Чжэньюй ; Лю, Сяо, Фаньцзинь ; 1–1 дои : 10.1109/ TKDE.2021.3090866 ISSN 1041-4347 .

[gpt1paper-3] Рэдфорд, Алек; Нарасимхан, Картик; Салиманс, Тим; Суцкевер, Илья (11 июня 2018 г.). «Улучшение понимания языка посредством генеративной предварительной подготовки» (PDF) . ОпенАИ . п. 12. Архивировано (PDF) из оригинала 26 января 2021 года . Проверено 23 января 2021 г.

[4] Ли, Чжохань; Уоллес, Эрик; Шен, Шэн; Лин, Кевин; Кейцер, Курт; Кляйн, Дэн; Гонсалес, Джоуи (21 ноября 2020 г.). «Обучайтесь больше, затем сжимайте: переосмысление размера модели для эффективного обучения и вывода трансформаторов» . Материалы 37-й Международной конференции по машинному обучению . ПМЛР: 5958–5968.

[Hinton2010-5] Хинтон, Г. (2012). «Практическое руководство по обучению ограниченных машин Больцмана» (PDF) . Нейронные сети: хитрости . Конспекты лекций по информатике. Том. 7700. Спрингер. стр. 599–619. дои : 10.1007/978-3-642-35289-8_32 . ISBN 978-3-642-35289-8 . Архивировано (PDF) из оригинала 3 сентября 2022 г. Проверено 3 ноября 2022 г.

[HintonMlss2009-6] Хинтон, Джеффри (сентябрь 2009 г.). «Сети глубокой веры» (видео). Архивировано из оригинала 8 марта 2022 г. Проверено 27 марта 2022 г.

[“nc95“-7] Питер, Даян ; Хинтон, Джеффри Э .; Нил, Рэдфорд М .; Земель, Ричард С. (1995). «Машина Гельмгольца». Нейронные вычисления . 7 (5): 889–904. дои : 10.1162/neco.1995.7.5.889 . hdl : 21.11116/0000-0002-D6D3-E . ПМИД 7584891 . S2CID 1890561 .

[Buhmann-8] Буманн, Дж.; Кунель, Х. (1992). «Неконтролируемая и контролируемая кластеризация данных с помощью конкурентных нейронных сетей». [Труды 1992 г.] Международная совместная конференция IJCNN по нейронным сетям . Том. 4. ИИЭР. стр. 796–801. дои : 10.1109/ijcnn.1992.227220 . ISBN 0780305590 . S2CID 62651220 .

[Comesana-9] Комесанья-Кампос, Альберто; Буза-Родригес, Хосе Бенито (июнь 2016 г.). «Применение Хеббианского обучения при принятии решений в процессе проектирования». Журнал интеллектуального производства . 27 (3): 487–506. дои : 10.1007/s10845-014-0881-z . ISSN 0956-5515 . S2CID 207171436 .

[Carpenter-10] Карпентер, Джорджия, и Гроссберг, С. (1988). «ИСКУССТВО адаптивного распознавания образов с помощью самоорганизующейся нейронной сети» (PDF) . Компьютер . 21 (3): 77–88. дои : 10.1109/2.33 . S2CID 14625094 . Архивировано из оригинала (PDF) 16 мая 2018 г. Проверено 16 сентября 2013 г.

[tds-ul-11] Роман, Виктор (21 апреля 2019 г.). «Машинное обучение без учителя: кластерный анализ» . Середина . Архивировано из оригинала 21 августа 2020 г. Проверено 1 октября 2019 г.

[JordanBishop2004-12] Джордан, Майкл И.; Бишоп, Кристофер М. (2004). «7. Интеллектуальные системы §Нейронные сети». В Такере, Аллен Б. (ред.). Справочник по информатике (2-е изд.). Чепмен и Холл/CRC Press. дои : 10.1201/9780203494455 . ISBN 1-58488-360-Х . Архивировано из оригинала 3 ноября 2022 г. Проверено 3 ноября 2022 г.

[Hastie-13] Хасти, Тибширани и Фридман, 2009 , стр. 485–586.

[tds-kmeans-14] Гарбаде, доктор Майкл Дж. (12 сентября 2018 г.). «Понимание кластеризации K-средних в машинном обучении» . Середина . Архивировано из оригинала 28 мая 2019 г. Проверено 31 октября 2019 г.

[TensorLVMs-15] Анандкумар, Анимашри; Ге, Ронг; Сюй, Дэниел; Какаде, Шам; Тельгарский, Матус (2014). «Тензорные разложения для изучения моделей со скрытыми переменными» (PDF) . Журнал исследований машинного обучения . 15 : 2773–2832. arXiv : 1210.7559 . Бибкод : 2012arXiv1210.7559A . Архивировано (PDF) из оригинала 20 марта 2015 г. Проверено 10 апреля 2015 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]