B 5 Многогранник
 5-куб |  5-ортоплекс | 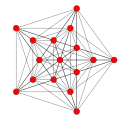 5-демикуб |
В 5-мерной геометрии существует 31 однородный многогранник с B5 симметрией . Существуют две правильные формы: 5-ортоплекс и 5-куб с 10 и 32 вершинами соответственно. добавлен 5-куб как чередование 5-куба.
Их можно визуализировать как симметричные ортогональные проекции в плоскостях Кокстера группы B 5 Кокстера и других подгрупп.
Графики
[ редактировать ]Симметричные ортогональные проекции этих 32 многогранников можно построить в плоскостях B 5 , B 4 , B 3 , B 2 , A 3 , Кокстера . A k имеет симметрию [k+1] , а B k имеет симметрию [2k] .
Каждый из этих 32 многогранников показан в этих 5 плоскостях симметрии, с нарисованными вершинами и ребрами, а вершины окрашены в соответствии с количеством перекрывающихся вершин в каждой проективной позиции.
| # | График Б 5 / А 4 [10] | График Б 4 / Д 5 [8] | График Б3 / А2 [6] | График BБ2 [4] | График AА3 [4] | Диаграмма Кокстера-Динкина и символ Шлефли Имена Джонсона и Бауэрса |
|---|---|---|---|---|---|---|
| 1 |  |  | 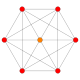 | 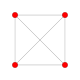 | 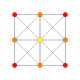 | ч{4,3,3,3} 5-демикуб Гемипентеракт (хин) |
| 2 |  |  | 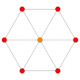 | 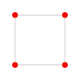 | 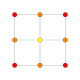 | {4,3,3,3} 5-куб Пентеракт (пентеракт) |
| 3 |  | 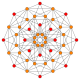 |  | 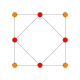 | 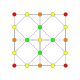 | т 1 {4,3,3,3} = r{4,3,3,3} Ректифицированный 5-куб Пентеракт ректификованный (рин) |
| 4 |  | 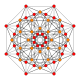 | 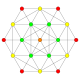 | 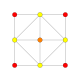 |  | т 2 {4,3,3,3} = 2r{4,3,3,3} Биректифицированный 5-куб Пентерактитриаконтидитерон (нит) |
| 5 |  | 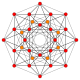 | 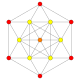 |  |  | т 1 {3,3,3,4} = r{3,3,3,4} Выпрямленный 5-ортоплекс Ректифицированный триаконтидитерон (крыса) |
| 6 |  | 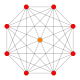 | 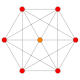 |  |  | {3,3,3,4} 5-ортоплекс Триаконтидитерон (так) |
| 7 |  | 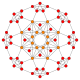 | 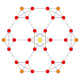 |  |  | т 0,1 {4,3,3,3} = т{3,3,3,4} Усеченный 5-куб Усеченный пентеракт (тан) |
| 8 |  |  | 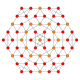 | 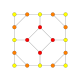 |  | т 1,2 {4,3,3,3} = 2т {4,3,3,3} Битусеченный 5-куб Усеченный пентеракт (биттин) |
| 9 |  | 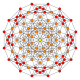 | 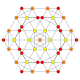 |  | 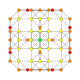 | т 0,2 {4,3,3,3} = рр{4,3,3,3} Согнутый 5-куб Ромбированный пентеракт (сирн) |
| 10 |  |  |  | 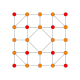 | 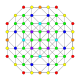 | т 1,3 {4,3,3,3} = 2рр{4,3,3,3} Двускатный 5-куб Малый биромби-пентерактитриаконтидитерон (сибрант) |
| 11 |  | 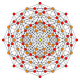 | 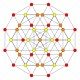 | 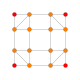 | 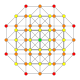 | т 0,3 {4.3,3.3} Ранцинированный 5-кубовый Призматический пентеракт (пролет) |
| 12 |  | 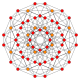 | 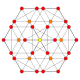 |  | 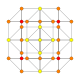 | т 0,4 {4,3,3,3} = 2r2r{4,3,3,3} Стерилизованный 5-куб. Мелкий целли-пентерактитриаконтидитерон (скудный) |
| 13 |  | 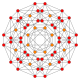 | 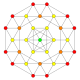 | 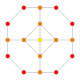 | 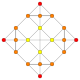 | т 0,1 {3,3,3,4} = т{3,3,3,4} Усеченный 5-ортоплекс Усеченный триаконтидитерон (тот) |
| 14 |  |  | 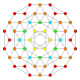 | 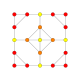 | 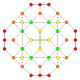 | т 1,2 {3,3,3,4} = 2т {3,3,3,4} Битусеченный 5-ортоплекс Усеченный триаконтидитерон (биттит) |
| 15 |  |  | 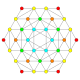 |  | 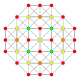 | т 0,2 {3,3,3,4} = рр{3,3,3,4} Сочлененный 5-ортоплекс Маленький ромбовидный триаконтидитерон (сарт) |
| 16 |  |  | 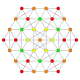 |  | 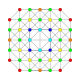 | т 0,3 {3,3,3,4} Ранцинированный 5-ортоплекс Маленький призматичный триаконтидитерон (плюна) |
| 17 |  |  | 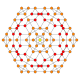 | 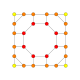 | 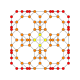 | т 0,1,2 {4,3,3,3} = тр{4,3,3,3} Количественный усеченный 5-куб Большой ромбовидный пентеракт (гирн) |
| 18 |  |  | 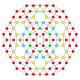 | 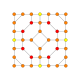 | 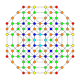 | т 1,2,3 {4,3,3,3} = тр{4,3,3,3} Бикантиусеченный 5-куб Большой биромби-пентерактитриаконтидитерон (гибрант) |
| 19 |  |  | 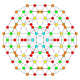 | 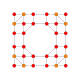 | 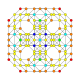 | т 0,1,3 {4,3,3,3} Ранцитусеченный 5-куб Призматоусеченный пентеракт (паттин) |
| 20 |  |  |  | 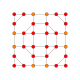 | 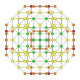 | т 0,2,3 {4,3,3,3} Рунцикантеллярный 5-куб Призматороматный пентеракт (распечатать) |
| 21 |  | 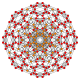 | 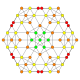 | 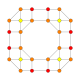 | 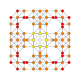 | т 0,1,4 {4,3,3,3} Стерильный усеченный 5-куб. Целлитусеченный пентеракт (капт) |
| 22 |  | 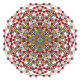 | 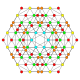 | 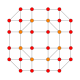 | 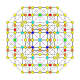 | т 0,2,4 {4,3,3,3} Стериконтеллярный 5-кубовый Целлиромби-пентерактитриаконтидитерон (карнит) |
| 23 |  |  | 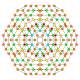 | 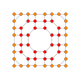 | 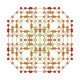 | т 0,1,2,3 {4,3,3,3} Ранцикантиусеченный 5-куб Пентеракт больших приматов (гиппин) |
| 24 |  |  | 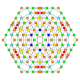 | 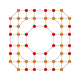 | 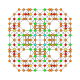 | т 0,1,2,4 {4,3,3,3} Стерикантиусеченный 5-кубовый Целлигреатор ромбовидный пентеракт (когрин) |
| 25 |  |  | 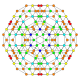 | 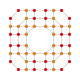 | 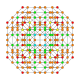 | т 0,1,3,4 {4,3,3,3} Стерильныйусеченный 5-куб. Целлипризматорунки-пентерактитриаконтидитерон (каптинт) |
| 26 |  |  | 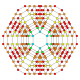 |  | 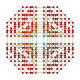 | т 0,1,2,3,4 {4,3,3,3} Всеусеченный 5-куб Большой целли-пентерактитриаконтидитерон (гакнет) |
| 27 |  |  | 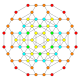 | 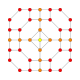 | 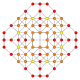 | т 0,1,2 {3,3,3,4} = тр{3,3,3,4} Кантиусеченный 5-ортоплекс Большой ромбовидный триаконтидитерон (гарт) |
| 28 |  |  | 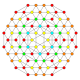 | 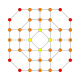 | 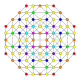 | т 0,1,3 {3,3,3,4} Ранцитусеченный 5-ортоплекс Призматоусеченный триаконтидитерон (паттит) |
| 29 |  |  | 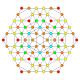 |  |  | т 0,2,3 {3,3,3,4} Рунцикантеллярный 5-ортоплекс Призматоромбатированный триаконтидитерон (пирт) |
| 30 |  | 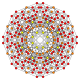 | 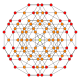 | 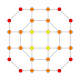 | 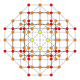 | т 0,1,4 {3,3,3,4} Стеритусеченный 5-ортоплекс Целлитусеченный триаконтидитерон (каппин) |
| 31 |  |  |  | 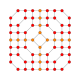 | 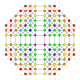 | т 0,1,2,3 {3,3,3,4} Ранцикантиусеченный 5-ортоплекс Большой призматорромбовидный триаконтидитерон (гиппит) |
| 32 |  |  | 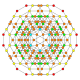 |  |  | т 0,1,2,4 {3,3,3,4} Стерикантиусеченный 5-ортоплекс Целлигреаторромбовидный триаконтидитерон (когарт) |
Ссылки
[ редактировать ]- ХСМ Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
Внешние ссылки
[ редактировать ]- Клитцинг, Ричард. «5D однородные многогранники (политеры)» .