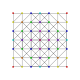| # | Диаграмма Кокстера-Динкина
Символ Шлефли
Имя Джонсона | A k ортогональных проекций графы |
|---|
А 8
[9] | A 7
[8] | А 6
[7] | AА5
[6] | A 4
[5] | AА3
[4] | AА2
[3] |
|---|
| 1 |               
т 0 {3,3,3,3,3,3,3}
8-симплекс |  |  |  |  |  |  | 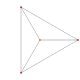 |
|---|
| 2 |               
т 1 {3,3,3,3,3,3,3}
Выпрямленный 8-симплекс |  |  |  | 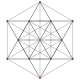 |  |  | 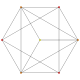 |
|---|
| 3 |               
т 2 {3,3,3,3,3,3,3}
Биректифицированный 8-симплекс |  | 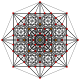 |  |  |  |  |  |
|---|
| 4 |               
т 3 {3,3,3,3,3,3,3}
Триректифицированный 8-симплекс | 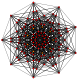 |  |  |  |  |  |  |
|---|
| 5 |               
т 0,1 {3,3,3,3,3,3,3}
Усеченный 8-симплекс |  |  |  | 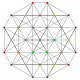 |  | 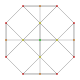 |  |
|---|
| 6 |               
т 0,2 {3.3.3.3.3.3.3}
Сочлененный 8-симплекс |  |  |  |  |  |  | 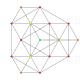 |
|---|
| 7 |               
т 1,2 {3,3,3,3,3,3,3}
Битусеченный 8-симплекс |  | 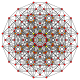 |  |  | 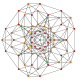 |  |  |
|---|
| 8 |               
т 0,3 {3.3.3.3.3.3.3}
Ранцинированный 8-симплекс |  |  |  | 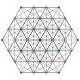 |  |  |  |
|---|
| 9 |               
т 1,3 {3,3,3,3,3,3,3}
Двукантельчатый 8-симплекс |  |  | 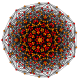 |  | 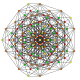 |  |  |
|---|
| 10 |               
т 2,3 {3,3,3,3,3,3,3}
Трехусеченный 8-симплекс |  |  |  |  | 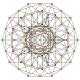 |  |  |
|---|
| 11 |               
т 0,4 {3.3.3.3.3.3.3}
Стерический 8-симплекс |  |  |  |  |  |  |  |
|---|
| 12 |               
т 1,4 {3,3,3,3,3,3,3}
Бирунцированный 8-симплекс |  |  |  | 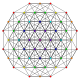 |  |  |  |
|---|
| 13 |               
т 2,4 {3,3,3,3,3,3,3}
Треугольный 8-симплекс |  |  | 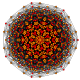 |  |  |  |  |
|---|
| 14 |               
т 3,4 {3,3,3,3,3,3,3}
Четырехусеченный 8-симплекс |  |  |  |  |  | 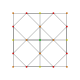 |  |
|---|
| 15 |               
т 0,5 {3,3,3,3,3,3,3}
Пятеричный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 16 |               
т 1,5 {3,3,3,3,3,3,3}
Бистерифицированный 8-симплекс |  |  |  | 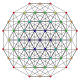 |  |  |  |
|---|
| 17 |               
т 2,5 {3,3,3,3,3,3,3}
Трехгранный 8-симплекс |  |  |  |  |  |  | 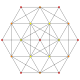 |
|---|
| 18 |               
т 0,6 {3.3.3.3.3.3.3}
Шестигранный 8-симплекс | 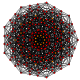 |  | 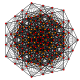 |  |  |  |  |
|---|
| 19 |               
т 1,6 {3,3,3,3,3,3,3}
Двупятнистый 8-симплекс |  |  | 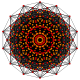 | 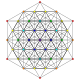 |  |  | 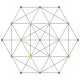 |
|---|
| 20 |               
т 0,7 {3,3,3,3,3,3,3}
Гептеллированный 8-симплекс |  |  | 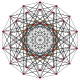 |  |  |  |  |
|---|
| 21 |               
т 0,1,2 {3,3,3,3,3,3,3}
Количественно усеченный 8-симплекс |  |  | 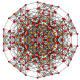 |  | 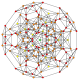 |  |  |
|---|
| 22 |               
т 0,1,3 {3,3,3,3,3,3,3}
Runcitусеченный 8-симплекс |  |  |  | 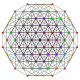 |  |  |  |
|---|
| 23 |               
т 0,2,3 {3,3,3,3,3,3,3}
Рунцикантеллярный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 24 |               
т 1,2,3 {3,3,3,3,3,3,3}
Бикантиусеченный 8-симплекс |  |  | 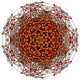 |  |  |  |  |
|---|
| 25 |               
т 0,1,4 {3,3,3,3,3,3,3}
Стеритусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 26 |               
т 0,2,4 {3,3,3,3,3,3,3}
Стериконтеллярный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 27 |               
т 1,2,4 {3,3,3,3,3,3,3}
Бирюроусеченный 8-симплекс |  |  |  | 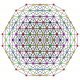 |  | 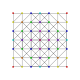 |  |
|---|
| 28 |               
т 0,3,4 {3,3,3,3,3,3,3}
Стерильный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 29 |               
т 1,3,4 {3,3,3,3,3,3,3}
Бирунчикантеллированный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 30 |               
т 2,3,4 {3,3,3,3,3,3,3}
Трикантиусеченный 8-симплекс |  |  |  |  |  | 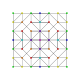 |  |
|---|
| 31 |               
т 0,1,5 {3,3,3,3,3,3,3}
Пятиусеченный 8-симплекс |  | 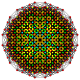 | 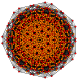 |  |  |  |  |
|---|
| 32 |               
т 0,2,5 {3,3,3,3,3,3,3}
Пятиконтеллярный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 33 |               
т 1,2,5 {3,3,3,3,3,3,3}
Бистериусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 34 |               
т 0,3,5 {3,3,3,3,3,3,3}
Пятислойный 8-симплекс | 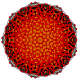 |  |  |  |  |  |  |
|---|
| 35 |               
т 1,3,5 {3,3,3,3,3,3,3}
Бистерикантеллированный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 36 |               
т 2,3,5 {3,3,3,3,3,3,3}
Трехгранный усеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 37 |               
т 0,4,5 {3,3,3,3,3,3,3}
Пентистерифицированный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 38 |               
т 1,4,5 {3,3,3,3,3,3,3}
Бистерирцинтированный 8-симплекс |  |  | 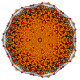 |  | 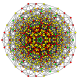 |  |  |
|---|
| 39 |               
т 0,1,6 {3,3,3,3,3,3,3}
Шестиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 40 |               
т 0,2,6 {3,3,3,3,3,3,3}
Шестикантеллярный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 41 |               
т 1,2,6 {3,3,3,3,3,3,3}
Бипентиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 42 |               
т 0,3,6 {3,3,3,3,3,3,3}
Шестистержневой 8-симплекс |  |  | 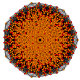 |  |  |  | 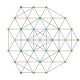 |
|---|
| 43 |               
т 1,3,6 {3,3,3,3,3,3,3}
Двупентикантеллированный 8-симплекс |  |  |  | 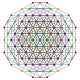 |  |  |  |
|---|
| 44 |               
т 0,4,6 {3,3,3,3,3,3,3}
Шестистеричный 8-симплекс |  |  |  |  | 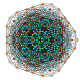 |  |  |
|---|
| 45 |               
т 0,5,6 {3,3,3,3,3,3,3}
Шестипятнистый 8-симплекс |  |  |  |  |  |  |  |
|---|
| 46 |               
т 0,1,7 {3,3,3,3,3,3,3}
Семиусеченный 8-симплекс |  |  |  |  |  | 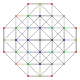 |  |
|---|
| 47 |               
т 0,2,7 {3,3,3,3,3,3,3}
Гептикантеллированный 8-симплекс |  |  |  |  |  |  | 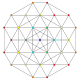 |
|---|
| 48 |               
т 0,3,7 {3,3,3,3,3,3,3}
Гептируссифицированный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 49 |               
т 0,1,2,3 {3,3,3,3,3,3,3}
Ранчикантиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 50 |               
т 0,1,2,4 {3,3,3,3,3,3,3}
Стерикантиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 51 |               
т 0,1,3,4 {3,3,3,3,3,3,3}
Стерирунный усеченный 8-симплекс |  |  | 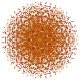 | 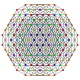 | 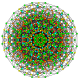 |  |  |
|---|
| 52 |               
т 0,2,3,4 {3,3,3,3,3,3,3}
Стерирунцикантеллярный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 53 |               
т 1,2,3,4 {3,3,3,3,3,3,3}
Бирунциантитусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 54 |               
т 0,1,2,5 {3,3,3,3,3,3,3}
Пентикантиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 55 |               
т 0,1,3,5 {3,3,3,3,3,3,3}
Пятиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 56 |               
т 0,2,3,5 {3,3,3,3,3,3,3}
Пятирунцикантеллярный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 57 |               
т 1,2,3,5 {3,3,3,3,3,3,3}
Бистерикантиусеченный 8-симплекс |  |  |  |  |  | 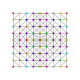 |  |
|---|
| 58 |               
т 0,1,4,5 {3,3,3,3,3,3,3}
Пентистеритусеченный 8-симплекс |  |  | 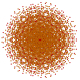 |  |  |  | 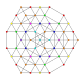 |
|---|
| 59 |               
т 0,2,4,5 {3,3,3,3,3,3,3}
Пентистерикантеллированный 8-симплекс |  |  |  |  | 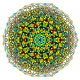 | 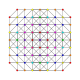 |  |
|---|
| 60 |               
т 1,2,4,5 {3,3,3,3,3,3,3}
Бистерирунцитусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 61 |               
т 0,3,4,5 {3,3,3,3,3,3,3}
Пентистерирцинтированный 8-симплекс |  |  |  | 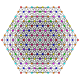 |  |  |  |
|---|
| 62 |               
т 1,3,4,5 {3,3,3,3,3,3,3}
Бистерирунцикантеллярный 8-симплекс |  |  |  | 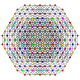 |  |  |  |
|---|
| 63 |               
т 2,3,4,5 {3,3,3,3,3,3,3}
Трирунцикантиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 64 |               
т 0,1,2,6 {3,3,3,3,3,3,3}
Гексикантиусеченный 8-симплекс |  |  |  | 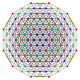 |  |  | 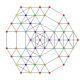 |
|---|
| 65 |               
т 0,1,3,6 {3,3,3,3,3,3,3}
Шестиусеченный 8-симплекс | 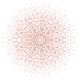 |  |  |  |  |  |  |
|---|
| 66 |               
т 0,2,3,6 {3,3,3,3,3,3,3}
Шестиграннокантеллярный 8-симплекс |  |  |  |  |  | 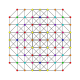 |  |
|---|
| 67 |               
т 1,2,3,6 {3,3,3,3,3,3,3}
Бипентикантиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 68 |               
т 0,1,4,6 {3,3,3,3,3,3,3}
Гексистеритусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 69 |               
т 0,2,4,6 {3,3,3,3,3,3,3}
Гексистерикантеллированный 8-симплекс |  |  | 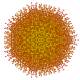 |  |  |  |  |
|---|
| 70 |               
т 1,2,4,6 {3,3,3,3,3,3,3}
Бипентирусеченный 8-симплекс |  |  |  |  | 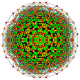 |  |  |
|---|
| 71 |               
т 0,3,4,6 {3,3,3,3,3,3,3}
Шестикруговой 8-симплекс |  |  |  |  |  |  |  |
|---|
| 72 |               
т 1,3,4,6 {3,3,3,3,3,3,3}
Бипентирунцикантеллярный 8-симплекс |  | 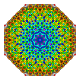 |  |  |  |  |  |
|---|
| 73 |               
т 0,1,5,6 {3,3,3,3,3,3,3}
Гексипентиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 74 |               
т 0,2,5,6 {3,3,3,3,3,3,3}
Гексипентикантеллированный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 75 |               
т 1,2,5,6 {3,3,3,3,3,3,3}
Бипентистеритусеченный 8-симплекс |  |  |  | 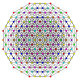 |  |  |  |
|---|
| 76 |               
т 0,3,5,6 {3,3,3,3,3,3,3}
Шестиперстёрчатый 8-симплекс |  |  |  |  |  |  |  |
|---|
| 77 |               
т 0,4,5,6 {3,3,3,3,3,3,3}
Гексипентистерифицированный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 78 |               
т 0,1,2,7 {3,3,3,3,3,3,3}
Гептикантитусеченный 8-симплекс |  |  |  | 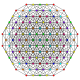 |  |  |  |
|---|
| 79 |               
т 0,1,3,7 {3,3,3,3,3,3,3}
Гептирусекулярный 8-симплекс |  |  |  |  | 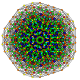 | 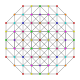 |  |
|---|
| 80 |               
т 0,2,3,7 {3,3,3,3,3,3,3}
Гептирунцикантеллярный 8-симплекс |  |  | 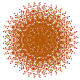 |  |  |  | 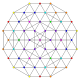 |
|---|
| 81 |               
т 0,1,4,7 {3,3,3,3,3,3,3}
Гептистеритусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 82 |               
т 0,2,4,7 {3,3,3,3,3,3,3}
Гептистерикантеллированный 8-симплекс |  |  | 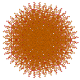 |  |  |  |  |
|---|
| 83 |               
т 0,3,4,7 {3,3,3,3,3,3,3}
Гептистерирцинтированный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 84 |               
т 0,1,5,7 {3,3,3,3,3,3,3}
Гептипентиусеченный 8-симплекс |  |  |  |  |  |  | 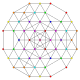 |
|---|
| 85 |               
т 0,2,5,7 {3,3,3,3,3,3,3}
Гептипентикантеллированный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 86 |               
т 0,1,6,7 {3,3,3,3,3,3,3}
Гептихекситусеченный 8-симплекс |  |  |  | 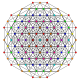 |  | 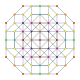 |  |
|---|
| 87 |               
т 0,1,2,3,4 {3,3,3,3,3,3,3}
Стерирунциантитусеченный 8-симплекс |  |  |  |  | 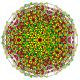 |  | 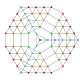 |
|---|
| 88 |               
т 0,1,2,3,5 {3,3,3,3,3,3,3}
Пятигранникантиусеченный 8-симплекс |  | 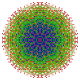 |  |  |  |  |  |
|---|
| 89 |               
т 0,1,2,4,5 {3,3,3,3,3,3,3}
Пентистерикантиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 90 |               
т 0,1,3,4,5 {3,3,3,3,3,3,3}
Пентистерирундусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 91 |               
т 0,2,3,4,5 {3,3,3,3,3,3,3}
Пентистерирунцикантеллярный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 92 |               
т 1,2,3,4,5 {3,3,3,3,3,3,3}
Бистерирунцикантиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 93 |               
т 0,1,2,3,6 {3,3,3,3,3,3,3}
Шестигранно-усеченный 8-симплекс |  |  |  |  |  | 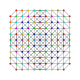 |  |
|---|
| 94 |               
т 0,1,2,4,6 {3,3,3,3,3,3,3}
Гексистерический усеченный 8-симплекс |  |  |  |  | 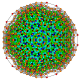 |  |  |
|---|
| 95 |               
т 0,1,3,4,6 {3,3,3,3,3,3,3}
Гексистерирундусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 96 |               
т 0,2,3,4,6 {3,3,3,3,3,3,3}
Гексистерирунцикантеллярный 8-симплекс |  |  |  | 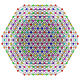 |  |  |  |
|---|
| 97 |               
т 1,2,3,4,6 {3,3,3,3,3,3,3}
Бипентирунцикантиусеченный 8-симплекс |  |  |  |  | 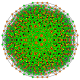 |  |  |
|---|
| 98 |               
т 0,1,2,5,6 {3,3,3,3,3,3,3}
Гексипентикантитусеченный 8-симплекс |  |  |  |  | 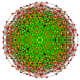 |  |  |
|---|
| 99 |               
т 0,1,3,5,6 {3,3,3,3,3,3,3}
Шестипериусеченный 8-симплекс | 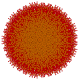 |  |  |  |  |  |  |
|---|
| 100 |               
т 0,2,3,5,6 {3,3,3,3,3,3,3}
Гексипентирунцикантеллированный 8-симплекс |  | 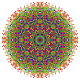 |  | 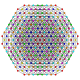 |  |  |  |
|---|
| 101 |               
т 1,2,3,5,6 {3,3,3,3,3,3,3}
Бипентистерикантиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 102 |               
т 0,1,4,5,6 {3,3,3,3,3,3,3}
Гексипентистеритусеченный 8-симплекс |  |  |  |  |  |  | 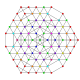 |
|---|
| 103 |               
т 0,2,4,5,6 {3,3,3,3,3,3,3}
Гексипентистерикантеллированный 8-симплекс |  |  |  | 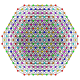 |  |  | 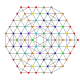 |
|---|
| 104 |               
т 0,3,4,5,6 {3,3,3,3,3,3,3}
Гексипентистерирцинтированный 8-симплекс |  |  |  |  | 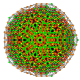 |  |  |
|---|
| 105 |               
т 0,1,2,3,7 {3,3,3,3,3,3,3}
Гептирунцикантиусеченный 8-симплекс |  |  |  |  | 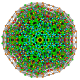 | 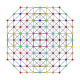 | 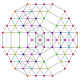 |
|---|
| 106 |               
т 0,1,2,4,7 {3,3,3,3,3,3,3}
Гептистерическийантитусеченный 8-симплекс |  | 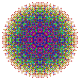 |  |  |  |  |  |
|---|
| 107 |               
т 0,1,3,4,7 {3,3,3,3,3,3,3}
Гептистерирундусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 108 |               
т 0,2,3,4,7 {3,3,3,3,3,3,3}
Гептистерирунцикантеллярный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 109 |               
т 0,1,2,5,7 {3,3,3,3,3,3,3}
Гептипентикантитусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 110 |               
т 0,1,3,5,7 {3,3,3,3,3,3,3}
Гептипентикумусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 111 |               
т 0,2,3,5,7 {3,3,3,3,3,3,3}
Гептипентикунтеллированный 8-симплекс |  |  |  | 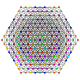 |  |  |  |
|---|
| 112 |               
т 0,1,4,5,7 {3,3,3,3,3,3,3}
Гептипентистеритусеченный 8-симплекс |  |  |  |  |  |  | 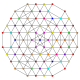 |
|---|
| 113 |               
т 0,1,2,6,7 {3,3,3,3,3,3,3}
Гептигексикантитусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 114 |               
т 0,1,3,6,7 {3,3,3,3,3,3,3}
Гептигексусеченно-усеченный 8-симплекс |  |  |  | 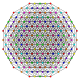 |  |  | 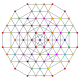 |
|---|
| 115 |               
т 0,1,2,3,4,5 {3,3,3,3,3,3,3}
Пентистерирунцикантиусеченный 8-симплекс |  | 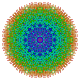 |  |  | 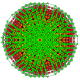 | 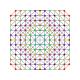 | 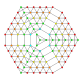 |
|---|
| 116 |               
т 0,1,2,3,4,6 {3,3,3,3,3,3,3}
Гексистерирунсикантиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 117 |               
т 0,1,2,3,5,6 {3,3,3,3,3,3,3}
Гексипентирунсикантиусеченный 8-симплекс |  |  |  |  | 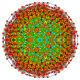 |  | 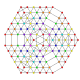 |
|---|
| 118 |               
т 0,1,2,4,5,6 {3,3,3,3,3,3,3}
Гексипентистерикантиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 119 |               
т 0,1,3,4,5,6 {3,3,3,3,3,3,3}
Гексипентистерирундусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 120 |               
т 0,2,3,4,5,6 {3,3,3,3,3,3,3}
Гексипентистерирунцикантеллярный 8-симплекс |  |  |  |  | 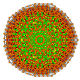 |  |  |
|---|
| 121 |               
т 1,2,3,4,5,6 {3,3,3,3,3,3,3}
Бипентистерирунсикантиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 122 |               
т 0,1,2,3,4,7 {3,3,3,3,3,3,3}
Гептистерирунсикантиусеченный 8-симплекс |  |  |  |  |  | 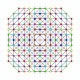 |  |
|---|
| 123 |               
т 0,1,2,3,5,7 {3,3,3,3,3,3,3}
Гептипентикунтитусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 124 |               
т 0,1,2,4,5,7 {3,3,3,3,3,3,3}
Гептипентистериантитусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 125 |               
т 0,1,3,4,5,7 {3,3,3,3,3,3,3}
Гептипентистерирундусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 126 |               
т 0,2,3,4,5,7 {3,3,3,3,3,3,3}
Гептипентистерирунцикантеллярный 8-симплекс |  |  |  |  |  |  | 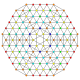 |
|---|
| 127 |               
т 0,1,2,3,6,7 {3,3,3,3,3,3,3}
Гептихексирансикантиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 128 |               
т 0,1,2,4,6,7 {3,3,3,3,3,3,3}
Гептихексистерикантитусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 129 |               
т 0,1,3,4,6,7 {3,3,3,3,3,3,3}
Гептихексистерирундусеченный 8-симплекс |  |  |  |  |  |  | 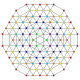 |
|---|
| 130 |               
т 0,1,2,5,6,7 {3,3,3,3,3,3,3}
Гептихексипентикантитусеченный 8-симплекс |  |  |  |  |  | 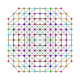 | 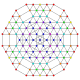 |
|---|
| 131 |               
т 0,1,2,3,4,5,6 {3,3,3,3,3,3,3}
Гексипентистерирунцикантиусеченный 8-симплекс |  |  |  |  |  |  |  |
|---|
| 132 |               
т 0,1,2,3,4,5,7 {3,3,3,3,3,3,3}
Гептипентистерирунцикантиусеченный 8-симплекс |  |  |  |  |  | 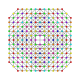 |  |
|---|
| 133 |               
т 0,1,2,3,4,6,7 {3,3,3,3,3,3,3}
Гептихексистерирунцикантиусеченный 8-симплекс |  |  |  |  |  |  | 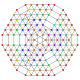 |
|---|
| 134 |               
т 0,1,2,3,5,6,7 {3,3,3,3,3,3,3}
Гептигексипентикурансикантиусеченный 8-симплекс |  |  |  | 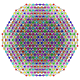 |  |  |  |
|---|
| 135 |               
т 0,1,2,3,4,5,6,7 {3,3,3,3,3,3,3}
Всеусеченный 8-симплекс |  |  |  |  |  | 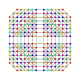 | 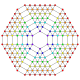 |
|---|