H-дерево

Не путать с HTree , структурой индексации файловой системы Linux.

Первые десять уровней H-дерева

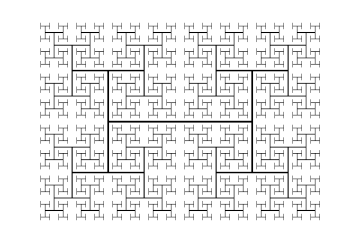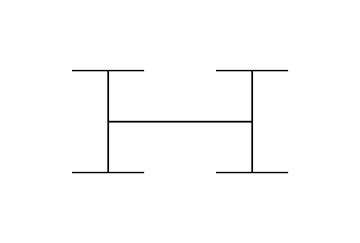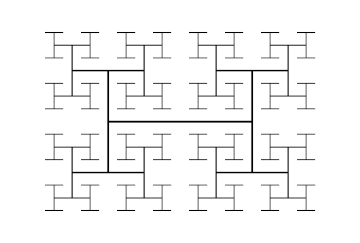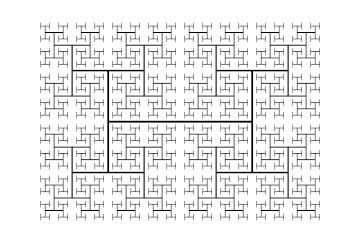
Во фрактальной геометрии представляет H-дерево собой фрактальную древовидную структуру, построенную из перпендикулярных отрезков прямой , каждый из которых меньше в квадратный корень из 2 раз из следующего большего соседнего сегмента. Он назван так потому, что его повторяющийся узор напоминает букву «Н». Он имеет размерность Хаусдорфа 2 и подходит сколь угодно близко к каждой точке прямоугольника . Его приложения включают проектирование СБИС и микроволновую технику.

Строительство

H-дерево можно построить, начав с отрезка произвольной длины, нарисовав два более коротких отрезка под прямым углом к ​​первому через его конечные точки и продолжив в том же духе, уменьшая (разделяя) длину отрезков, нарисованных на каждом из них. поэтапно ${\sqrt {2}}$. Можно также определить вариант этой конструкции, в котором длина на каждой итерации умножается на коэффициент, меньший, чем $1/{\sqrt {2}}$, но в этом варианте результирующая фигура покрывает только часть ограничивающего ее прямоугольника с фрактальной границей.

Альтернативный процесс, который генерирует тот же фрактальный набор, — начать с прямоугольника со сторонами в соотношении $1:{\sqrt {2}}$и несколько раз разделите его пополам на два меньших серебряных прямоугольника, на каждом этапе соединяя два центроида двух меньших прямоугольников отрезком линии. Аналогичный процесс можно проделать с прямоугольниками любой другой формы, но $1:{\sqrt {2}}$ прямоугольника приводит к равномерному уменьшению размера отрезка на ${\sqrt {2}}$ на каждом шаге, в то время как для остальных прямоугольников длина будет уменьшаться в разные разы на нечетном и четном уровнях рекурсивной конструкции.

Характеристики

Дерево H представляет собой самоподобный фрактал ; его хаусдорфова размерность равна 2.

Точки H-дерева подходят сколь угодно близко к каждой точке прямоугольника ( так же, как исходный прямоугольник при построении по центроидам разделенных прямоугольников). Однако он не включает все точки прямоугольника; например, точки на серединном перпендикуляре начального отрезка (кроме середины этого отрезка) не включаются.

Приложения

При проектировании СБИС H-дерево может использоваться в качестве макета полного двоичного дерева, общая площадь которого пропорциональна количеству узлов дерева. Кроме того, H-дерево образует компактную компоновку деревьев при рисовании графов . и как часть построения набора точек, для которого сумма квадратов длин ребер путешествия коммивояжера велика. Он обычно используется в качестве сети распределения тактовых импульсов для маршрутизации сигналов синхронизации ко всем частям микросхемы с одинаковыми задержками распространения для каждой части. а также использовался в качестве сети соединения для мультипроцессоров СБИС.

Трехмерное H-дерево

Плоское дерево H можно обобщить до трехмерной структуры путем добавления отрезков линий в направлении, перпендикулярном плоскости дерева H. Полученное трехмерное H-дерево имеет размерность Хаусдорфа, равную 3. Было обнаружено, что планарное H-дерево и его трехмерная версия составляют искусственные электромагнитные атомы в фотонных кристаллах и метаматериалах и могут иметь потенциальное применение в микроволновой технике.

Похожие наборы

14 ступеней дерева Fractal Canopy, анимированные.

Дерево H — это пример фрактального навеса , в котором угол между соседними сегментами линий всегда равен 180 градусам. По своему свойству подходить сколь угодно близко к каждой точке ограничивающего его прямоугольника он также напоминает кривую, заполняющую пространство , хотя сам по себе не является кривой.

Топологически H-дерево имеет свойства, аналогичные свойствам дендроида . Однако они не являются дендроидами: дендроиды должны быть замкнутыми множествами , а H-деревья не являются замкнутыми (их замыканием является весь прямоугольник).

Вариации одной и той же древовидной структуры с утолщенными многоугольными ветвями вместо отрезков линии дерева H были определены Бенуа Мандельбротом и иногда называются деревом Мандельброта. В этих вариантах, чтобы избежать перекрытия листьев дерева и их утолщенных ветвей, масштабный коэффициент, на который уменьшается размер на каждом уровне, должен быть немного больше, чем ${\sqrt {2}}$.

Ссылки

• Берн, Маршалл; Эппштейн, Дэвид (1993), «Оценки наихудшего случая для субаддитивных геометрических графов», Proc. 9-й ежегодный симпозиум по вычислительной геометрии (PDF) , Ассоциация вычислительной техники , стр. 183–188, doi : 10.1145/160985.161018 , S2CID   14158914 .
• Браунинг, Салли А. (1980), Древовидная машина: высокопараллельная вычислительная среда , доктор философии. диссертация, Калифорнийский технологический институт, заархивировано из оригинала 16 июля 2012 г. , получено 28 ноября 2012 г.
• Буркис, Дж. (1991), «Синтез дерева часов для высокопроизводительных ASIC», Международная конференция IEEE по ASIC , стр. 9.8.1–9.8.4, doi : 10.1109/ASIC.1991.242921 , S2CID   60985695 .
• Хоу, Бо; Се, Ханг; Вэнь, Вейцзя; Шэн, Пинг (2008), «Трехмерные металлические фракталы и их фотонно-кристаллические характеристики» (PDF) , Physical Review B , 77 (12): 125113, doi : 10.1103/PhysRevB.77.125113 .
• Калошин Вадим; Сапрыкина, Мария (2012), «Пример почти интегрируемой гамильтоновой системы с траекторией, плотной в множестве максимальной хаусдорфовой размерности», Communications in Mathematical Physics , 315 (3): 643–697, doi : 10.1007/s00220-012 -1532-x , MR   2981810 , S2CID   253737197 .
• Лауверье, Ганс (1991), Фракталы: бесконечно повторяющиеся геометрические фигуры , Принстонская научная библиотека, том. 6, перевод Гилл-Хоффштадта, Софии, Princeton University Press, ISBN  9780691024455
• Лейзерсон, Чарльз Э. (1980), «Эффективные по площади макеты графов», 21-й ежегодный симпозиум по основам информатики (FOCS 1980) , стр. 270–281, doi : 10.1109/SFCS.1980.13 , S2CID   15532332 .
• Нгуен, Куанг Винь; Хуан, Мао Линь (2002), «Визуализация дерева, оптимизированная для пространства», Симпозиум IEEE по визуализации информации , стр. 85–92, doi : 10.1109/INFVIS.2002.1173152 , S2CID   22192509 .
• Уллман, Джеффри Д. (1984), Вычислительные аспекты VSLI , Computer Science Press .
• Вэнь, Вейцзя; Чжоу, Лэй; Ли, Дженсен; Ге, Вэйкунь; Чан, Коннектикут; Шэн, Пинг (2002), «Субволновые фотонные запрещенные зоны из плоских фракталов» (PDF) , Physical Review Letters , 89 (22): 223901, doi : 10.1103/PhysRevLett.89.223901 , PMID   12485068 .