Косой апейроэдр
В геометрии косой апейроэдр — это бесконечный косой многогранник, состоящий из неплоских граней или неплоских вершинных фигур , что позволяет фигуре расширяться до бесконечности, не сгибаясь и образуя замкнутую поверхность .
Косые апейроэдры также называют многогранными губками .
Многие из них напрямую связаны с выпуклыми однородными сотами , представляющими собой многоугольную поверхность сот с некоторыми ячейками удаленными . Характерно, что бесконечный косой многогранник делит трехмерное пространство на две половины. Если одна половина считается сплошной, фигуру иногда называют частичной сотой .
Правильные косые апейроэдры
[ редактировать ]По мнению Коксетера , в 1926 году Джон Флиндерс Петри обобщил понятие правильных косых многоугольников (неплоских многоугольников) на правильные косые многогранники (апейроэдры). [1]
Коксетер и Петри нашли три из них, заполнившие трехмерное пространство:
| Правильные косые апейроэдры | ||
|---|---|---|
 {4,6|4} мукуб |  {6,4|4} муоктаэдр |  {6,6|3} мутетраэдр |
Существуют также киральные косые апейроэдры типов {4,6}, {6,4} и {6,6}. Эти косые апейроэдры являются вершинно-транзитивными , реберно-транзитивными и гране-транзитивными , но не зеркально-симметричными ( Schulte 2004 ).
Помимо евклидова трехмерного пространства, в 1967 году К.У.Л. Гарнер опубликовал набор из 31 правильного косого многогранника в гиперболическом трехмерном пространстве. [2]
Правильные псевдомногогранники Готта
[ редактировать ]Дж. Ричард Готт в 1967 году опубликовал более крупный набор из семи бесконечных косых многогранников, которые он назвал правильными псевдомногогранниками , включая три из Коксетера как {4,6}, {6,4} и {6,6} и четыре новых: {5,5}, {4,5}, {3,8}, {3,10}. [3] [4]
Готт смягчил определение регулярности, чтобы использовать свои новые цифры. Если Коксетер и Петри требовали, чтобы вершины были симметричны, Готт требовал только, чтобы они были конгруэнтны. Таким образом, новые примеры Готта не являются регулярными по определению Коксетера и Петри.
Готт назвал полный набор правильных многогранников , правильных мозаик и правильных псевдомногогранников правильными обобщенными многогранниками {p,q} , представимыми символом Шлефли , с p-угольными гранями q вокруг каждой вершины. Однако ни термин «псевдополиэдр», ни определение регулярности, данное Готтом, не получили широкого распространения.
Кристаллограф А. Ф. Уэллс в 1960-х годах также опубликовал список скошенных апейроэдров. Мелинда Грин опубликовала еще много книг в 1998 году.
| {п, д} | Клетки вокруг вершины | Вертекс лица | Больше шаблон | Космическая группа | Связанные Н 2 орбифолд обозначение | ||
|---|---|---|---|---|---|---|---|
| Кубический космос группа | Коксетер обозначение | Фибрифолд обозначение | |||||
| {4,5} | 3 кубика |  |  | мне 3 метра | [[4,3,4]] | 8°:2 | *4222 |
| {4,5} | 1 усеченный октаэдр 2 шестиугольные призмы |  | я 3 | [[4,3 + ,4]] | 8°:2 | 2*42 | |
| {3,7} | 1 октаэдр 1 икосаэдр |  |  | FdFd3 | [[3 [4] ]] + | 2° − | 3222 |
| {3,8} | 2 курносых кубика |  |  | FM 3 м | [4,(3,4) + ] | 2 −− | 32* |
| {3,9} | 1 тетраэдр 3 октаэдра |  |  | Фд 3 м | [[3 [4] ]] | 2 + :2 | 2*32 |
| {3,9} | 1 икосаэдр 2 октаэдра |  | я 3 | [[4,3 + ,4]] | 8°:2 | 22*2 | |
| {3,12} | 5 октаэдров |  |  | мне 3 метра | [[4,3,4]] | 8°:2 | 2*32 |
Призматические формы
[ редактировать ] Призматическая форма: {4,5} |
Существуют две призматические формы:
- {4,5}: 5 квадратов в вершине (две параллельные квадратные мозаики, соединенные кубическими отверстиями).
- {3,8}: 8 треугольников в вершине (две параллельные треугольные мозаики, соединенные октаэдрическими отверстиями).
Другие формы
[ редактировать ]{3,10} также формируется из параллельных плоскостей треугольных плиток с чередующимися октаэдрическими отверстиями, идущими в обе стороны.
{5,5} состоит из трёх копланарных пятиугольников вокруг вершины и двух перпендикулярных пятиугольников, заполняющих зазор.
Готт также признал, что существуют и другие периодические формы регулярных плоских мозаик. Как квадратная плитка {4,4}, так и треугольная плитка {3,6} могут быть изогнуты в аппроксимирующие бесконечные цилиндры в трехмерном пространстве.
Теоремы
[ редактировать ]Он написал несколько теорем:
- Для каждого правильного многогранника {p,q}: (p-2)*(q-2)<4. Для каждой регулярной мозаики: (p-2)*(q-2)=4. Для каждого правильного псевдополиэдра: (p-2)*(q-2)>4.
- В любом правильном обобщенном многограннике количество граней, окружающих данную грань, равно p*(q-2).
- Каждый правильный псевдополиэдр аппроксимирует поверхность отрицательной кривизны.
- Семь правильных псевдополиэдров представляют собой повторяющиеся структуры.
Равномерный косой апейроэдр
[ редактировать ]Существует множество других равномерных ( вершинно-транзитивных ) косых апейроэдров. Вахманн, Берт и Кляйнманн (1974) обнаружили множество примеров, но неизвестно, полон ли их список.
Некоторые из них проиллюстрированы здесь. Их можно назвать по конфигурации вершин , хотя это не уникальное обозначение косых форм.
| 4.4.6.6 | 6.6.8.8 | |
|---|---|---|
 |  |  |
| Относящийся к изогнутым кубическим сотам , | Относящийся к рунцикантическим кубическим сотам , | |
| 4.4.4.6 | 4.8.4.8 | 3.3.3.3.3.3.3 |
 |  |  |
| Относительно всеусеченных кубических сот : | ||
| 4.4.4.6 | 4.4.4.8 | 3.4.4.4.4 |
 | 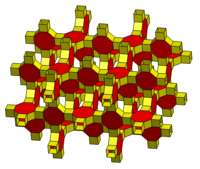 |  Относится к усеченным кубическим сотам . |
| 4.4.4.4.4 | 4.4.4.6 |
|---|---|
 Связано с |  Связано с |
Другие можно построить как дополненные цепочки многогранников:
  |  |
| Униформа Спираль Бурдейка – Кокстера | Стеки кубиков |
|---|
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Коксетер, HSM Правильные косые многогранники в трех и четырех измерениях. Учеб. Лондонская математика. Соц. 43, 33–62, 1937.
- ^ Гарнер, Правильные косые многогранники CWL в гиперболическом трехмерном пространстве. Может. Дж. Математика. 19, 1179–1186, 1967. [1] Архивировано 2 апреля 2015 г. в Wayback Machine.
- ^ Дж. Р. Готт, Псевдополиэдры, American Mathematical Monthly, том 74, стр. 497-504, 1967.
- ^ Симметрии вещей, Псевдоплатонические многогранники, стр.340-344.
- Коксетер , Правильные многогранники , Третье издание, (1973), Дуврское издание, ISBN 0-486-61480-8
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Документ 2) HSM Coxeter, «Правильные губки, или косые многогранники», Scripta Mathematica 6 (1939) 240–244.
- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус , (2008) Симметрии вещей , ISBN 978-1-56881-220-5 (Глава 23, Объекты простой симметрии, псевдоплатонические многогранники, p340-344)
- Шульте, Эгон (2004), «Киральные многогранники в обычном пространстве. I», Дискретная и вычислительная геометрия , 32 (1): 55–99, doi : 10.1007/s00454-004-0843-x , MR 2060817 . [3] Архивировано 4 марта 2016 г. в Wayback Machine.
- А. Ф. Уэллс, Трехмерные сети и многогранники , Wiley, 1977. [4]
- А. Вахманн, М. Берт и М. Кляйнманн, Бесконечные многогранники , Технион, 1974. 2-е изд. 2005.
- Э. Шульте, Дж. М. Уиллс о правильных косых многогранниках Коксетера , Дискретная математика, том 60, июнь – июль 1986 г., страницы 253–262
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Правильный косой многогранник» . Математический мир .
- Вайсштейн, Эрик В. «Соты и губки» . Математический мир .
- Ольшевский, Георгий. «Перекос многогранника» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
- «Гиперболические» тесселяции
- Бесконечные правильные многогранники [5]. Архивировано 12 марта 2016 г. в Wayback Machine.
- Бесконечные повторяющиеся многогранники — частичные соты в трехмерном пространстве
- 18 СИММЕТРИЯ МНОГОГРАННИКОВ И МНОГОГРАННИКОВ, Эгон Шульте: 18.3 ПРАВИЛЬНЫЕ СКОРЫЕ МНОГОГРАННИКИ
- Бесконечные многогранники, Т.Э. Дорозинский