✖


Jump to content

Треугольник Рело

Это хорошая статья. Нажмите здесь для получения дополнительной информации.
(Перенаправлено с Reuleaux hendecagon )

Граница треугольника Рело представляет собой кривую постоянной ширины, основанную на равностороннем треугольнике. Все точки стороны равноудалены от противоположной вершины.

Треугольник Рело [ʁœlo] — изогнутый треугольник постоянной ширины , самая простая и известная кривая постоянной ширины, кроме круга. [1] Он образован пересечением трех круглых дисков , центр каждого из которых находится на границе двух других. Постоянная ширина означает, что расстояние между всеми двумя параллельными опорными линиями одинаково, независимо от их ориентации. Поскольку его ширина постоянна, треугольник Рело является одним из ответов на вопрос: «Какую форму, кроме круга, можно сделать крышкой люка , чтобы она не могла упасть через отверстие?» [2]

Они названы в честь Франца Рёло . [3] немецкий инженер XIX века, пионер изучения машин для преобразования одного типа движения в другой и использовавший в своих конструкциях треугольники Рело. [4] Однако эти формы были известны и до него, например, дизайнерам готических церковных окон, Леонардо да Винчи , который использовал их для картографической проекции , и Леонарду Эйлеру в его исследовании форм постоянной ширины. Другие применения треугольника Рело включают придание формы медиаторам , пожарных гидрантов гайкам , карандашам и сверлам для сверления скругленных квадратных отверстий, а также в графическом дизайне в форме некоторых знаков и корпоративных логотипов.

Среди фигур постоянной ширины с заданной шириной треугольник Рело имеет минимальную площадь и самый острый (наименьший) возможный угол (120 °) в углах. По нескольким численным показателям он наиболее далек от центрально-симметричного . Он обеспечивает наибольшую форму постоянной ширины, избегая точек целочисленной решетки , и тесно связан с формой четырехугольника, максимизируя соотношение периметра к диаметру. Он может совершать полный оборот внутри квадрата, постоянно касаясь всех четырех сторон квадрата, и имеет наименьшую возможную площадь фигур с этим свойством. Однако, хотя в этом процессе вращения он покрывает большую часть квадрата, ему не удается покрыть небольшую часть площади квадрата вблизи его углов. Из-за этого свойства вращения внутри квадрата треугольник Рело также иногда называют ротором Рело . [5]

Треугольник Рело — первый из последовательности многоугольников Рело , границы которых представляют собой кривые постоянной ширины, образованные из правильных многоугольников с нечетным числом сторон. Некоторые из этих кривых использовались в качестве форм монет . Треугольник Рело также можно обобщить на три измерения несколькими способами: тетраэдр Рело (пересечение четырех шаров , центры которых лежат на правильном тетраэдре ) не имеет постоянной ширины, но может быть изменен путем закругления его краев, чтобы сформировать тетраэдр Мейснера. , что и делает. Альтернативно, поверхность вращения треугольника Рело также имеет постоянную ширину.

Строительство

[ редактировать ]
Чтобы построить треугольник Рело

Треугольник Рело может быть построен либо непосредственно из трех кругов , либо путем округления сторон равностороннего треугольника . [6]

Построение трех кругов можно выполнить только с помощью циркуля , даже не используя линейку. По теореме Мора–Машерони то же самое верно и в более общем плане для любой конструкции, состоящей из циркуля и линейки . [7] но конструкция треугольника Рело особенно проста.Первый шаг — отметить две произвольные точки плоскости (которые в конечном итоге станут вершинами треугольника) и с помощью циркуля провести круг с центром в одной из отмеченных точек через другую отмеченную точку. Затем рисуется второй круг того же радиуса с центром в другой отмеченной точке и проходящий через первую отмеченную точку.Наконец, рисуется третий круг, снова того же радиуса, с центром в одной из двух точек пересечения двух предыдущих кругов, проходящий через обе отмеченные точки. [8] Центральной областью получившегося расположения трех кругов будет треугольник Рело. [6]

Альтернативно, треугольник Рело можно построить из равностороннего треугольника T, нарисовав три дуги окружностей, каждая из которых сосредоточена в одной вершине треугольника T и соединив две другие вершины. [9] центрами в вершинах T и радиусом, равным длине стороны T. Или, что то же самое, его можно построить как пересечение трех дисков с [10]

Математические свойства

[ редактировать ]
Параллельные опорные линии треугольника Рело

Самым основным свойством треугольника Рело является то, что он имеет постоянную ширину, а это означает, что для каждой пары параллельных опорных линий (двух линий с одинаковым наклоном, которые касаются фигуры, не пересекая ее) две линии имеют одинаковое евклидово расстояние от друг друга, независимо от ориентации этих линий. [9] В любой паре параллельных опорных линий одна из двух линий обязательно будет касаться треугольника в одной из его вершин. Другая опорная линия может касаться треугольника в любой точке противоположной дуги, а расстояние между ними (ширина треугольника Рело) равно радиусу этой дуги. [11]

Первым математиком, открывшим существование кривых постоянной ширины и заметившим, что треугольник Рело имеет постоянную ширину, возможно, был Леонард Эйлер . [5] В статье, которую он представил в 1771 году и опубликовал в 1781 году под названием De curvis triangularibus , Эйлер изучил криволинейные треугольники, а также кривые постоянной ширины, которые он назвал орбиформами. [12] [13]

Экстремальные меры

[ редактировать ]

По многим параметрам треугольник Рело является одной из самых крайних кривых постоянной ширины.

По теореме Бляшке-Лебега треугольник Рело имеет наименьшую возможную площадь среди любой кривой заданной постоянной ширины. Эта область

где s — постоянная ширина. Один из методов вывода этой формулы площади состоит в том, чтобы разделить треугольник Рело на внутренний равносторонний треугольник и три криволинейные области между этим внутренним треугольником и дугами, образующими треугольник Рело, а затем сложить площади этих четырех наборов. С другой стороны, кривая постоянной ширины, имеющая максимально возможную площадь, представляет собой круглый диск , площадь которого . [14]

Все углы, образованные каждой парой дуг в углах треугольника Рело, равны 120 °. Это максимально острый угол в любой вершине любой кривой постоянной ширины. [9] Кроме того, среди кривых постоянной ширины треугольник Рело имеет как самый большой, так и самый маленький вписанные равносторонние треугольники. [15] Самый большой равносторонний треугольник, вписанный в треугольник Рело, — это тот, который соединяет три его угла, а самый маленький — тот, который соединяет три середины его сторон. Подмножество треугольника Рело, состоящее из точек, принадлежащих трем или более диаметрам, является внутренней частью большего из этих двух треугольников; она имеет большую площадь, чем набор точек трех диаметров любой другой кривой постоянной ширины. [16]

Центрально-симметричные формы внутри и снаружи треугольника Рело, используемые для измерения его асимметрии.

Хотя треугольник Рело обладает шестигранной двугранной симметрией , так же, как и равносторонний треугольник , он не имеет центральной симметрии .Треугольник Рело представляет собой наименее симметричную кривую постоянной ширины в соответствии с двумя различными мерами центральной асимметрии: мерой Ковнера-Безиковича (отношение площади к наибольшей центрально-симметричной форме, заключенной в кривую) и мерой Эстермана (отношение площади к площади наименьшая центрально-симметричная форма, охватывающая кривую). В треугольнике Рело две центрально-симметричные фигуры, определяющие меру асимметрии, являются шестиугольными , хотя внутренняя имеет изогнутые стороны. [17] Треугольник Рело имеет диаметры, которые делят его площадь более неравномерно, чем любая другая кривая постоянной ширины. То есть максимальное соотношение площадей по обе стороны диаметра, еще одна мера асимметрии, для треугольника Рело больше, чем для других кривых постоянной ширины. [18]

Среди всех фигур постоянной ширины, которые избегают всех точек целочисленной решетки , наибольшую ширину имеет треугольник Рело. Одна из его осей симметрии параллельна осям координат на полуцелой прямой. Его ширина, примерно 1,54, является корнем многочлена шестой степени с целыми коэффициентами. [17] [19] [20]

Точно так же, как круг может быть окружен шестью конгруэнтными окружностями, которые соприкасаются с ним, также возможно расположить семь конгруэнтных треугольников Рело так, чтобы все они соприкасались с центральным треугольником Рело того же размера. Это максимально возможное число для любой кривой постоянной ширины. [21]

Равнодиагональный воздушный змей с максимальным соотношением периметра к диаметру, вписанный в треугольник Рело.

Среди всех четырехугольников фигурой, которая имеет наибольшее отношение периметра к диаметру , является равнодиагональный змей , который можно вписать в треугольник Рело. [22]

Другие меры

[ редактировать ]

По теореме Барбье все кривые одинаковой постоянной ширины, включая треугольник Рело, имеют равные периметры . В частности, этот периметр равен периметру круга той же ширины, который . [23] [24] [9]

Радиусы наибольшей вписанной окружности треугольника Рело шириной s и описанной окружности того же треугольника равны

соответственно; сумма этих радиусов равна ширине треугольника Рело. В более общем смысле, для каждой кривой постоянной ширины наибольшая вписанная окружность и наименьшая описанная окружность концентричны, а сумма их радиусов равна постоянной ширине кривой. [25]

Нерешенная задача по математике :
Насколько плотно можно упаковать треугольники Рело в плоскости?
(еще нерешенные задачи по математике)

Оптимальная плотность упаковки треугольника Рело в плоскости остается недоказанной, но предполагается, что она равна

что представляет собой плотность одной возможной двойной решетчатой ​​упаковки для этих форм. Наилучшая доказанная верхняя граница плотности упаковки составляет примерно 0,947. [26] Также было высказано предположение, но не доказано, что треугольники Рело имеют самую высокую плотность упаковки среди всех кривых постоянной ширины. [27]

Вращение внутри квадрата

[ редактировать ]
Вращение треугольника Рело внутри квадрата, а также кривая, очерченная центром треугольника.

Любая кривая постоянной ширины может образовывать ротор внутри квадрата , форму, которая может совершать полный оборот, оставаясь внутри квадрата и постоянно касаясь всех четырех сторон квадрата. Однако треугольник Рело — это ротор минимально возможной площади. [9] Когда он вращается, его ось не остается фиксированной в одной точке, а следует по кривой, образованной частями четырех эллипсов . [28] Из-за своих углов в 120° вращающийся треугольник Рело не может достичь некоторых точек вблизи более острых углов в вершинах квадрата, а скорее охватывает форму со слегка закругленными углами, также образованную эллиптическими дугами. [9]

Треугольник Рело в квадрате с эллипсом, определяющим траекторию движения центра треугольника.
Один из четырех эллипсов, за которым следует центр вращающегося треугольника Рело в квадрате.
Треугольник Рело в квадрате с эллипсом, ограничивающим область, охваченную треугольником.
Эллипс, отделяющий один из углов (внизу слева) квадрата от области, охваченной вращающимся треугольником Рело.

В любой момент этого вращения два угла треугольника Рело касаются двух соседних сторон квадрата, а третий угол треугольника очерчивает кривую возле противоположной вершины квадрата. Форма, очерченная вращающимся треугольником Рело, занимает примерно 98,8% площади квадрата. [29]

В качестве контрпримера

[ редактировать ]

Первоначальной мотивацией Рело к изучению треугольника Рело был контрпример, показывающий, что трех одноточечных контактов может быть недостаточно для фиксации плоского объекта в одном положении. [30] Существование треугольников Рело и других кривых постоянной ширины показывает, что одни только измерения диаметра не могут подтвердить, что объект имеет круглое поперечное сечение. [31]

с проблемой вписанного квадрата В связи Эгглстон (1958) заметил, что треугольник Рело представляет собой пример формы постоянной ширины, в которую не может быть вписан ни один правильный многоугольник с более чем четырьмя сторонами, за исключением правильного шестиугольника, и описал небольшой модификацию этой формы, которая сохраняет ее постоянную ширину, но также предотвращает вписывание в нее правильных шестиугольников. Он обобщил этот результат на три измерения, используя цилиндр той же формы, что и его поперечное сечение . [32]

Приложения

[ редактировать ]

Достигая углов

[ редактировать ]

Некоторые типы машин имеют форму треугольника Рело, основанного на его свойстве вращаться внутри квадрата.

Watts Brothers Tool Works Квадратное сверло имеет форму треугольника Рело, модифицированного вогнутостями для образования режущих поверхностей. При установке в специальный патрон, который позволяет сверлу не иметь фиксированного центра вращения, можно просверлить отверстие почти квадратной формы. [33] Хотя подобные сверла были запатентованы Генри Уоттсом в 1914 году, они использовались и раньше. [9] Другие полигоны Рело используются для сверления пятиугольных, шестиугольных и восьмиугольных отверстий. [9] [33]

Panasonic RULO от Робот-пылесос имеет форму треугольника Рело, что облегчает уборку пыли в углах комнат. [34] [35]

Прокатные цилиндры

[ редактировать ]
Сравнение цилиндрического катка и треугольного катка Рело.

Другой класс применений треугольника Рело включает цилиндрические объекты с поперечным сечением треугольника Рело. Некоторые карандаши производятся именно этой формы, а не более традиционных круглых или шестиугольных корпусов. [36] Их обычно рекламируют как более удобные или способствующие правильному захвату, а также как менее склонные к скатыванию со стола (поскольку центр тяжести перемещается вверх и вниз больше, чем катящийся шестиугольник).

Треугольник Рело (как и все другие кривые постоянной ширины ) может катиться, но из него получается плохое колесо, поскольку он не вращается вокруг фиксированного центра вращения. Объект, находящийся на роликах треугольного сечения Рело, будет катиться плавно и ровно, но ось, прикрепленная к треугольным колесам Рело, будет подпрыгивать вверх и вниз три раза за оборот. [9] [37] Эта концепция была использована в научно-фантастическом рассказе Пола Андерсона под названием «Треугольное колесо». [11] [38] Велосипед с плавающими осями и рамой, поддерживаемой ободом колеса треугольной формы Рело, был построен и продемонстрирован в 2009 году китайским изобретателем Гуань Байхуа, которого вдохновили карандаши такой же формы. [39]

Конструкция механизма

[ редактировать ]
Механизм продвижения пленки в советском 8-мм кинопроекторе Луч-2 на основе треугольника Рело.

Другой класс применений треугольника Рело предполагает использование его как части механической связи , которая может преобразовывать вращение вокруг фиксированной оси. в возвратно-поступательное движение . [10] Эти механизмы изучал Франц Рело. При содействии компании Густава Фойгта Рело построил около 800 моделей механизмов, некоторые из которых включали треугольник Рело. [40] Рело использовал эти модели в своих новаторских научных исследованиях их движения. [41] Хотя большая часть моделей Рёло-Фойгта утеряна, 219 из них были собраны в Корнелльском университете , в том числе девять на основе треугольника Рёло. [40] [42] Однако использование треугольников Рело в конструкции механизмов предшествовало работам Рело; например, некоторые паровые машины, выпущенные еще в 1830 году, имели кулачок в форме треугольника Рело. [43] [44]

Одно из применений этого принципа возникает в кинопроекторе . В этом приложении необходимо продвигать пленку рывками, ступенчато, при этом каждый кадр пленки останавливается на долю секунды перед объективом проектора, а затем гораздо быстрее пленка перемещается к следующему. рамка. Это можно сделать с помощью механизма, в котором вращение треугольника Рело внутри квадрата используется для создания схемы движения привода, который быстро подтягивает пленку к каждому новому кадру, а затем приостанавливает движение пленки на время проецирования кадра. [45]

Ротор двигателя Ванкеля имеет форму криволинейного треугольника, который часто называют примером треугольника Рело. [3] [5] [9] [44] Однако его изогнутые стороны несколько более плоские, чем у треугольника Рело, поэтому он не имеет постоянной ширины. [46]

Архитектура

[ редактировать ]
Треугольное окно Рело в церкви Богоматери, Брюгге , Бельгия.

В готической архитектуре , начиная с конца 13 или начала 14 века, [47] Треугольник Рело стал одной из нескольких криволинейных форм, часто используемых для окон, оконного узора и других архитектурных украшений. [3] Например, в английской готической архитектуре эта форма была связана с периодом украшений, как в геометрическом стиле 1250–1290 годов, так и в криволинейном стиле 1290–1350 годов. [47] Он также появляется в некоторых окнах Миланского собора . [48] В этом контексте форму иногда называют сферическим треугольником . [47] [49] [50] который не следует путать со сферическим треугольником, означающим треугольник на поверхности сферы . При использовании в готической церковной архитектуре трехугольная форма треугольника Рело может рассматриваться как символ Троицы , [51] и как «акт противодействия форме круга». [52]

Треугольник Рело также использовался в других стилях архитектуры. Например, Леонардо да Винчи нарисовал эту форму как план укрепления. [42] Современные здания, которые, как утверждается, используют план этажа в форме треугольника Рело, включают аудиторию MIT Kresge Auditorium , Kölntriangle , Donauturm , Torre de Collserola и музей Mercedes-Benz . [53] Однако во многих случаях это просто закругленные треугольники с геометрией, отличной от треугольника Рело.

картографирование

[ редактировать ]
Основная статья: октантная проекция

Еще одно раннее применение треугольника Рело, карта мира да Винчи, датированная примерно 1514 годом, представляла собой карту мира , на которой сферическая поверхность Земли была разделена на восемь октантов, каждый из которых имел форму треугольника Рело. [54] [55] [56]

Карта мира Леонардо да Винчи в восьми квадрантах треугольника Рело.

Подобные карты, также основанные на треугольнике Рело, были опубликованы Оронсом Фине в 1551 году и Джоном Ди в 1580 году. [56]

Другие объекты

[ редактировать ]
Reuleaux треугольной формы. Медиаторы для гитары

Во многих медиаторах используется треугольник Рело, поскольку его форма сочетает в себе острую часть, обеспечивающую сильную артикуляцию, и широкий кончик, обеспечивающий теплый тембр. Поскольку все три точки формы пригодны для использования, ее легче ориентировать и она изнашивается медленнее по сравнению с киркой с одним кончиком. [57]

Незаконное использование пожарного гидранта, Филадельфия, 1996 год, и более нового гидранта из Филадельфии с треугольной гайкой Рело для предотвращения такого использования.

Треугольник Рело использовался в качестве формы поперечного сечения гайки клапана пожарного гидранта . Постоянная ширина такой формы затрудняет открытие пожарного гидранта стандартными ключами с параллельными губками; вместо этого необходим гаечный ключ особой формы. Это свойство позволяет открывать пожарные гидранты только пожарным (у которых есть специальный гаечный ключ), а не другим людям, пытающимся использовать гидрант в качестве источника воды для других действий. [58]

Субмиллиметровая решетка с семью из восьми антенн, расположенных примерно в треугольнике Рело.

Следуя предложению Кето (1997) , [59] антенны Submillimeter Array , радиоволновой астрономической обсерватории на Мауна-Кеа на Гавайях , расположены на четырех вложенных друг в друга треугольниках Рело. [60] [61] Размещение антенн на кривой постоянной ширины приводит к тому, что обсерватория имеет одинаковое пространственное разрешение во всех направлениях и обеспечивает круговой луч наблюдения. Треугольник Рело, являющийся наиболее асимметричной кривой постоянной ширины, приводит к наиболее равномерному покрытию плоскости для преобразования Фурье сигнала от массива. [59] [61] Усики можно перемещать из одного треугольника Рело в другой для разных наблюдений в соответствии с желаемым угловым разрешением каждого наблюдения. [60] [61] Точное расположение усиков на этих треугольниках Рело было оптимизировано с помощью нейронной сети . В некоторых местах построенная обсерватория отклоняется от предпочтительной формы треугольника Рело, поскольку такая форма была невозможна на данном участке. [61]

Знаки и логотипы

[ редактировать ]

Формы щитов, используемые для многих знаков и корпоративных логотипов, представляют собой закругленные треугольники. Однако лишь некоторые из них являются треугольниками Рело.

Корпоративный логотип Petrofina (Fina), бельгийской нефтяной компании с основными операциями в Европе, Северной Америке и Африке, использовал треугольник Рело с названием Fina с 1950 года до слияния Petrofina с Total SA (сегодня TotalEnergies ) в 2000 году. [62] [63] Еще один корпоративный логотип, обрамленный треугольником Рело, компасом пивоварни Bavaria Brewery , указывающим на юг , был частью реконструкции дизайнерской компании Total Identity, которая выиграла награду SAN «Рекламодатель года 2010». [64] Треугольник Рело также используется в логотипе Горной школы Колорадо . [65]

В Соединенных Штатах Национальная система троп и Система велосипедных маршрутов США отмечают маршруты треугольниками Рело на указателях. [66]

На природе

[ редактировать ]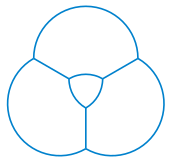
Треугольник Рело как центральный пузырь в математической модели плоского кластера мыльных пузырей из четырех пузырей.

Согласно законам Плато , дуги окружностей в двумерных скоплениях мыльных пузырей встречаются под углом 120° — тот же угол, что и в углах треугольника Рело. На основании этого факта можно построить кластеры, в которых часть пузырьков принимает форму треугольника Рело. [67]

Форма была впервые выделена в кристаллической форме в 2014 году в виде треугольных дисков Рело. [68] Базовые диски нитрата висмута формы треугольника Рело были сформированы в результате гидролиза и осаждения нитрата висмута в системе этанол–вода в присутствии 2,3-бис(2-пиридил)пиразина.

Обобщения

[ редактировать ]

Треугольные кривые постоянной ширины с гладкими, а не острыми углами могут быть получены как геометрические точки точек, находящихся на фиксированном расстоянии от треугольника Рело. [69] Другие обобщения треугольника Рело включают трехмерные поверхности, кривые постоянной ширины с более чем тремя сторонами и множества Янмути, которые представляют собой крайние примеры неравенства между шириной, диаметром и внутренним радиусом.

Трехмерная версия

[ редактировать ]
Четыре шара пересекаются, образуя тетраэдр Рело.

Пересечение четырех шаров радиуса s с центрами в вершинах правильного тетраэдра с длиной стороны s называется тетраэдром Рело , но его поверхность не является поверхностью постоянной ширины . [70] Однако его можно превратить в поверхность постоянной ширины, называемую тетраэдром Мейсснера , заменив три его краевые дуги изогнутыми поверхностями, поверхностями вращения дуги окружности. Альтернативно, поверхность вращения треугольника Рело через одну из его осей симметрии образует поверхность постоянной ширины с минимальным объемом среди всех известных поверхностей вращения заданной постоянной ширины. [71]

Полигоны Рело

[ редактировать ]
Основная статья: Полигон Рело
Полигоны Рело
Гамбии даласи Рело -семиугольник Монета

Треугольник Рело можно обобщить на правильные или неправильные многоугольники с нечетным числом сторон, в результате чего получается многоугольник Рело , кривая постоянной ширины, образованная из дуг окружностей постоянного радиуса. Постоянная ширина этих форм позволяет использовать их в качестве монет, которые можно использовать в монетоприемниках. [9] Хотя монеты этого типа, находящиеся в общем обращении, обычно имеют более трех сторон, треугольник Рело использовался для памятной монеты с Бермудских островов . [53]

Аналогичные методы можно использовать для заключения произвольного простого многоугольника в кривую постоянной ширины, ширина которой равна диаметру данного многоугольника. Полученная форма состоит из дуг окружностей (не более, чем количество сторон многоугольника), может быть построена алгоритмически за линейное время и может быть нарисована с помощью циркуля и линейки. [72] Хотя все многоугольники Рело имеют нечетное количество сторон дуги окружности, можно построить фигуры постоянной ширины с четным числом сторон дуги окружности различных радиусов. [73]

Наборы Янмути

[ редактировать ]

Множества Янмути определяются как выпуклые оболочки равностороннего треугольника вместе с тремя круговыми дугами с центрами в вершинах треугольника и охватывающими тот же угол, что и треугольник, с равными радиусами, которые не более чем равны длине стороны треугольника. Таким образом, когда радиус достаточно мал, эти множества вырождаются до самого равностороннего треугольника, но когда радиус максимально велик, они равны соответствующему треугольнику Рело. Каждая форма с шириной w , диаметром d и внутренним радиусом r (радиусом наибольшего возможного круга, содержащегося в форме) подчиняется неравенству

и это неравенство становится равенством для множеств Янмути, показывая, что его невозможно улучшить. [74]

[ редактировать ]
Трикетра переплетается в узел-трилистник.

В классическом представлении диаграммы Венна из трех множеств в виде трех перекрывающихся кругов центральная область (представляющая элементы, принадлежащие всем трем наборам) принимает форму треугольника Рело. [3] Те же три круга образуют один из стандартных рисунков колец Борромео , трёх взаимно связанных колец, которые, однако, не могут быть реализованы как геометрические круги. [75] Части этих же кругов используются для формирования трикетры , фигуры из трех перекрывающихся полукругов (каждый два из которых образуют символ vesica piscis ), в центре которой снова находится треугольник Рело; [76] точно так же, как три круга диаграммы Венна могут переплетаться, образуя кольца Борромео, три круговые дуги трикетра могут переплетаться, образуя узел-трилистник . [77]

Родственники треугольника Рело возникают в задаче нахождения минимальной формы периметра, охватывающей фиксированную площадь и включающей три заданные точки на плоскости. При широком диапазоне выбора параметра площади оптимальным решением этой задачи будет изогнутый треугольник, три стороны которого представляют собой дуги окружностей равных радиусов. В частности, когда три точки равноудалены друг от друга и площадь равна площади треугольника Рело, треугольник Рело является оптимальным ограждением. [78]

Круглые треугольники — это треугольники с краями в форме дуги окружности, включая треугольник Рело, а также другие формы.Дельтовидная кривая — это еще один тип криволинейного треугольника, но в нем кривые, заменяющие каждую сторону равностороннего треугольника, являются вогнутыми, а не выпуклыми. Он не состоит из дуг окружностей, но может быть образован путем прокатки одного круга внутри другого, радиус которого в три раза больше. [79] Другие плоские формы с тремя изогнутыми сторонами включают арбелос , который состоит из трех полукругов с коллинеарными конечными точками. [80] и треугольник Безье . [81]

Треугольник Рело можно также интерпретировать как стереографическую проекцию одной треугольной грани сферического тетраэдра , Шварца . треугольник параметров со сферическими углами измерения и стороны сферической длины [67] [82]

Ссылки

[ редактировать ]
  1. ^ Гарднер (2014) называет его самым простым, а Грубер (1983 , стр. 59) называет его «самым печально известным».
  2. ^ Клее, Виктор (1971), «Формы будущего», The Two-Year College Mathematics Journal , 2 (2): 14–27, doi : 10.2307/3026963 , JSTOR   3026963 .
  3. ^ Jump up to: а б с д Альсина, Клауди; Нельсен, Роджер Б. (2011), Иконы математики: исследование двадцати ключевых изображений , Dolciani Mathematical Expositions, vol. 45, Математическая ассоциация Америки, с. 155 , ISBN  978-0-88385-352-8 .
  4. ^ Мун, ФК (2007), Машины Леонардо да Винчи и Франца Рело: кинематика машин от эпохи Возрождения до 20-го века , История механизмов и машиноведения, том. 2, Спрингер, ISBN  978-1-4020-5598-0 .
  5. ^ Jump up to: а б с Брайант, Джон; Сангвин, Крис (2011), Насколько кругл ваш круг?: Где встречаются инженерия и математика , Princeton University Press, стр. 190 , ISBN  978-0-691-14992-9 .
  6. ^ Jump up to: а б Ханн, Майкл (2014), Структура и форма в дизайне: критические идеи для творческой практики , A&C Black, стр. 34, ISBN  978-1-4725-8431-1 .
  7. ^ Хунгербюлер, Норберт (1994), «Краткое элементарное доказательство теоремы Мора-Машерони», American Mathematical Monthly , 101 (8): 784–787, CiteSeerX   10.1.1.45.9902 , doi : 10.2307/2974536 , JSTOR   2974536 , MR   1299166 .
  8. ^ Эта конструкция кратко описана Маором и Йостом (2014) , и ее можно увидеть, например, в видео Алекса Франке «Забавы с треугольниками Рело» , 21 августа 2011 г.
  9. ^ Jump up to: а б с д и ж г час я дж к Гарднер, Мартин (2014), «Глава 18: Кривые постоянной ширины», Узлы и кольца Борромео, повторяющиеся плитки и восемь ферзей , Новая математическая библиотека Мартина Гарднера, том. 4, Издательство Кембриджского университета, стр. 223–245, ISBN.  978-0-521-75613-6 .
  10. ^ Jump up to: а б Клее, Виктор ; Вагон, С. (1991), Старые и новые нерешенные проблемы плоской геометрии и теории чисел , Математические пояснения Дольчиани, том. 11, Издательство Кембриджского университета, с. 21, ISBN  978-0-88385-315-3 .
  11. ^ Jump up to: а б Маор, Эли; Йост, Ойген (2014), «46 Треугольник Рело», Beautiful Geometry , Princeton University Press, стр. 154–156, ISBN  978-1-4008-4833-1 .
  12. ^ Райх, Карин (2007), «Вклад Эйлера в дифференциальную геометрию и ее восприятие», в Брэдли, Роберт Э.; Сандифер, Эд (ред.), Леонард Эйлер: жизнь, работа и наследие , Исследования по истории и философии математики, том. 5, Elsevier, стр. 479–502, номер документа : 10.1016/S0928-2017(07)80026-0 , ISBN.  9780444527288 . См., в частности, раздел 1.4, «Орбиформы, 1781», стр. 484–485 .
  13. ^ Эйлер, Леонхард (1781), «О треугольных кривых» , Acta Academiae Scientiarum Imperialis Petropolitanae (на латыни), 1778 : 3–30 . См., в частности, стр. 7 для определения орбиформ.
  14. ^ Грубер, Питер М. (1983), Выпуклость и ее приложения , Биркхойзер, с. 67 , ISBN  978-3-7643-1384-5
  15. ^ Грубер (1983 , стр. 76)
  16. ^ Makeev, V. V. (2000), "An extremal property of the Reuleaux triangle", Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) , 267 (Geom. i Topol. 5): 152–155, 329, doi : 10.1023/A:1021287302603 , MR  1809823 , S2CID  116027099 .
  17. ^ Jump up to: а б Финч, Стивен Р. (2003), «8.10 Константы треугольника Рело» (PDF) , Математические константы , Энциклопедия математики и ее приложений, Cambridge University Press, стр. 513–514 , ISBN  978-0-521-81805-6 .
  18. ^ Громер, Х.; Валлен, Л.Дж. (2001), «Мера асимметрии для областей постоянной ширины», Вклад в алгебру и геометрию , 42 (2): 517–521, MR   1865537 .
  19. ^ Грубер (1983 , стр. 78)
  20. ^ Салли, GT (1969), «Максимальный набор постоянной ширины в решетке» , Pacific Journal of Mathematics , 28 (3): 669–674, doi : 10.2140/pjm.1969.28.669 , MR   0240724 .
  21. ^ Фейес Тот, Л. (1967), «О количестве равных дисков, которые могут касаться других дисков того же типа», Studia Scientiarum Mathematicarum Hungarica , 2 : 363–367, MR   0221388 ; Шопп Дж. (1970), «О числе Ньютона диска постоянной ширины», Studia Scientiarum Mathematicarum Hungarica (на немецком языке), 5 : 475–478, MR   0285983 .
  22. ^ Болл, Д.Г. (1973), «Обобщение π», The Mathematical Gazette , 57 (402): 298–303, doi : 10.2307/3616052 , JSTOR   3616052 , S2CID   125396664 ; Гриффитс, Дэвид; Калпин, Дэвид (1975), «Пи-оптимальные многоугольники», The Mathematical Gazette , 59 (409): 165–175, doi : 10.2307/3617699 , JSTOR   3617699 , S2CID   126325288 .
  23. ^ Лэй, Стивен Р. (2007), Выпуклые множества и их приложения , Дувр, теорема 11.11, стр. 81–82, ISBN  978-0-486-45803-8 .
  24. ^ Барбье, Э. (1860), «Заметка о проблеме с иглой и игре с закрытым суставом» (PDF) , Журнал чистой и прикладной математики , 2 и серия (на французском языке), 5 : 273–286 . См., в частности, стр. 283–285.
  25. ^ Лэй (2007) , Теорема 11.8, стр. 80–81 .
  26. ^ Слепой, Г.; Блинд, Р. (1983), «Оценка плотнейшей плотности упаковки с помощью треугольников Рело», Studia Scientiarum Mathematicarum Hungarica (на немецком языке), 18 (2–4): 465–469, MR   0787951 . Так что смотри Слепой, Г.; Блинд, Р. (1987), «Регулярные упаковки с треугольниками Рело», Результаты по математике (на немецком языке), 11 (1–2): 1–7, doi : 10.1007/BF03323256 , MR   0880190 , S2CID   121633860 .
  27. ^ Резникофф, Ховард Л. (2015), О кривых и поверхностях постоянной ширины , arXiv : 1504.06733 , Bibcode : 2015arXiv150406733R .
  28. ^ Гляйфтнер, Винфрид; Цайтлер, Герберт (май 2000 г.), «Треугольник Рело и его центр масс», Results in Mathematics , 37 (3–4): 335–344, doi : 10.1007/bf03322004 , S2CID   119600507 .
  29. ^ Пиковер, Клиффорд А. (2009), «Треугольник Рело», Книга математики: от Пифагора до 57-го измерения, 250 вех в истории математики , Sterling Publishing Company, стр. 266, ISBN  978-1-4027-5796-9 .
  30. ^ Луна (2007) , с. 239 .
  31. ^ Грановский, В.А.; Сирая, Т.Н., «Метрологическая прослеживаемость и качество измерений при промышленных испытаниях», Павезе, Ф.; Бэр, М.; Фильц-младший; Форбс, АБ; Пендрилл, Л.; Широно, К. (ред.), Передовые математические и вычислительные инструменты в метрологии и тестировании IX , World Scientific, стр. 194–201 . См., в частности, стр. 200 .
  32. ^ Эгглстон, Х.Г. (1958), «Цифры, вписанные в выпуклые множества», American Mathematical Monthly , 65 (2): 76–80, doi : 10.2307/2308878 , JSTOR   2308878 , MR   0097768 .
  33. ^ Jump up to: а б Как сверлить квадратные шестиугольные восьмиугольные пятиугольные отверстия , Уилмердинг, Пенсильвания: Watts Brothers Tool Works , 1950–1951 (брошюра на 27 страниц).
  34. ^ Мотидзуки, Такаси (22 января 2015 г.), «Panasonic представляет треугольный робот-пылесос» , Japan Real Time, Wall Street Journal .
  35. ^ Коксворт, Бен (3 марта 2015 г.), «Panasonic вступает в игру роботов-пылесосов с треугольным Руло» , Gizmag .
  36. ^ Гамбер, Джонни (26 апреля 2006 г.), «Обзор Staedtler Noris Ergosoft HB» , Pencil Revolution , получено 22 мая 2015 г.
  37. ^ Масферрер Леон, Клаудия; фон Вутенау Майер, Себастьян (декабрь 2005 г.), «Изобретая колесо заново: некруглые колеса», The Mathematical Intelligencer , 27 (4): 7–13, doi : 10.1007/bf02985852 .
  38. ^ Андерсон, Пол (октябрь 1963 г.), «Треугольное колесо», аналог , стр. 50–69.
  39. ^ Демпстер, Тайра (17 июня 2009 г.), китаец заново изобретает велосипед , Reuters
  40. ^ Jump up to: а б Мун, Фрэнсис К. (июль 1999 г.), Коллекция кинематических механизмов Рело в Корнельском университете (PDF) , Библиотека Корнельского университета, заархивировано из оригинала (PDF) 14 июня 2020 г.
  41. ^ Хендерсон, Дэвид В.; Таймина, Дайна (2007), «Ощущение значений в геометрии», в Синклере, Натали ; Пимм, Дэвид; Хиггинсон, Уильям (ред.), Математика и эстетика: новые подходы к древней близости , Книги CMS по математике, Springer, стр. 58–83, doi : 10.1007/978-0-387-38145-9_4 , hdl : 1813 /2714 , ISBN  978-0-387-38145-9 . См., в частности, стр. 81 .
  42. ^ Jump up to: а б Луна (2007 , стр. 241).
  43. ^ Луна (2007 , стр. 240)
  44. ^ Jump up to: а б Петерсон, Иварс (19 октября 1996 г.), «Rolling with Reuleaux» , MathTrek , ScienceNews . Перепечатано в Петерсон, Иварс (2002), Математические пути: от сюрреалистических чисел к магическим кругам , спектр MAA, Математическая ассоциация Америки , стр. 141–144, ISBN  978-0-88385-537-9 .
  45. ^ Лэй (2007) , с. 83 .
  46. ^ Грубер (1983 , стр. 80); Нэш, Дэвид Х. (март 1977 г.), «Геометрия роторного двигателя», Mathematics Magazine , 50 (2): 87–89, doi : 10.1080/0025570x.1977.11976621 ; Бадр, О.; Наик, С.; О'Каллаган, PW; Проберт, С.Д. (1991), «Роторные двигатели Ванкеля как расширительные устройства в паровых двигателях с циклом Ренкина», Applied Energy , 39 (1): 59–76, doi : 10.1016/0306-2619(91)90063-4 .
  47. ^ Jump up to: а б с Харт, Стивен (2010), Узоры на окнах средневековой церкви в Англии , Boydell & Brewer Ltd, стр. 63–64, ISBN  978-1-84383-533-2 .
  48. ^ Маркетти, Елена; Коста, Луиза Росси (2014), «Какая геометрия в Миланском соборе?», Уильямс, Ким; Оствальд, Майкл Дж. (ред.), Архитектура и математика от древности к будущему, Том I: От древности до 1500-х годов , Биркхойзер, стр. 509–534, номер документа : 10.1007/978-3-319-00137-1_35
  49. ^ Паркер, Джон Генри (1850 г.), Словарь терминов, используемых в греческой, римской, итальянской и готической архитектуре , том. 1 (5-е изд.), Лондон: Дэвид Роуг, с. 202 .
  50. ^ Берчетт, Э.С. (1876), Практическая плоская геометрия , Лондон и Глазго: Уильям Коллинз, сыновья и компания, подпись к табличке LV, рис. 6 .
  51. ^ Дюран, Гийом (1906), Символика церквей и церковных украшений: перевод первой книги Rationale Divinorum Officiorum (3-е изд.), Гиббингс, стр. lxxxviii .
  52. ^ Франкл, Пол; Кроссли, Пол (2000), Готическая архитектура , История искусства Пеликана, том. 19, Издательство Йельского университета, с. 146, ISBN  978-0-300-08799-4 .
  53. ^ Jump up to: а б Конти, Джузеппе; Паолетти, Рафаэлла (октябрь 2019 г.), «Треугольник Рело в архитектуре и приложениях», в Магнаги-Дельфино, Паола; Меле, Джампьеро; Норандо, Туллия (ред.), Лица геометрии: от Агнеси до Мирзахани , Конспект лекций по сетям и системам, Springer, стр. 79–89, номер номера : 10.1007/978-3-030-29796-1_7 , S2CID   209976466 .
  54. ^ Снайдер, Джон П. (1997), Сглаживание Земли: две тысячи лет картографических проекций , University of Chicago Press, стр. 40, ISBN  978-0-226-76747-5 .
  55. ^ Кеунинг, Йоханнес (январь 1955 г.), «История географических картографических проекций до 1600 г.», Imago Mundi , 12 (1): 1–24, doi : 10.1080/03085695508592085 , JSTOR   1150090 .
  56. ^ Jump up to: а б Бауэр, Дэвид И. (февраль 2012 г.), «Необычная проекция на одной из карт Джона Ди 1580 года» (PDF) , The Cartographic Journal , 49 (1): 55–61, doi : 10.1179/1743277411y.0000000015 , S2CID   129873912 .
  57. ^ Гувер, Уилл (ноябрь 1995 г.), Picks !: Красочная сага о старинных целлулоидных гитарных плектрах , Backbeat Books, стр. 32–33, ISBN  978-0-87930-377-8 .
  58. ^ Мартини, Хорст; Монтехано, Луис; Оливерос, Дебора (2019), Тела постоянной ширины: введение в выпуклую геометрию с приложениями , Биркхойзер, стр. 3, номер домена : 10.1007/978-3-030-03868-7 , ISBN  978-3-030-03866-3 , МР   3930585 , S2CID   127264210
  59. ^ Jump up to: а б Кето, Эрик (1997), «Формы интерферометров взаимной корреляции», The Astrophysical Journal , 475 (2): 843–852, Бибкод : 1997ApJ...475..843K , doi : 10.1086/303545 .
  60. ^ Jump up to: а б Бланделл, Раймонд (2007), «Субмиллиметровая решетка» (PDF) , Proc. 2007 Международный симпозиум по микроволновому оборудованию IEEE/MTT-S , стр. 1857–1860, doi : 10.1109/mwsym.2007.380132 , ISBN  978-1-4244-0687-6 , S2CID   41312640 .
  61. ^ Jump up to: а б с д Хо, Пол Т.П.; Моран, Джеймс М.; Ло, Квок Юнг (2004), «Субмиллиметровая решетка», The Astrophysical Journal , 616 (1): L1 – L6, arXiv : astro-ph/0406352 , Bibcode : 2004ApJ...616L...1H , doi : 10.1086 /423245 , S2CID   115133614 .
  62. ^ Гвиллиан, Сэм (16 мая 2015 г.), Интересные вещи: кривые постоянной ширины , Newport City Radio, заархивировано из оригинала 16 июня 2016 г.
  63. ^ «История логотипа Fina: от Petrofina до Fina» , Total: Group Presentation , Total SA, заархивировано из оригинала 26 декабря 2012 г. , получено 31 октября 2015 г.
  64. ^ «Global: Bavaria, Fundamental Rebranding Operation в Bavaria» , Total Identity , заархивировано из оригинала 30 июня 2015 г. , получено 27 июня 2015 г. {{citation}}: CS1 maint: неподходящий URL ( ссылка )
  65. ^ Фишер, Роланд Б. (весна 2002 г.), «M-blems: Объяснение логотипа» (PDF) , Mines: Журнал Горной школы Колорадо , том. 92, нет. 2, с. 29, заархивировано из оригинала 10 июля 2010 г. {{citation}}: CS1 maint: неподходящий URL ( ссылка )
  66. ^ Линдли, Джеффри А. (1 июня 2012 г.), «Информация: MUTCD — временное разрешение на факультативное использование альтернативного дизайна для знака велосипедного маршрута (M1-9) США (IA-15)» , Руководство по единообразному управлению дорожным движением. Устройства для улиц и автомагистралей: ресурсы , Министерство транспорта США, Федеральное управление шоссейных дорог , данные получены 20 августа 2018 г.
  67. ^ Jump up to: а б Моудс, Карл Д.; Камиен, Рэндалл Д. (2013), «Сферические пены в плоском пространстве», Soft Matter , 9 (46): 11078–11084, arXiv : 0810.5724 , Bibcode : 2013SMat....911078M , doi : 10.1039/c3sm51585k , S2CID   965 91302 .
  68. ^ Нг, ХГБ; Фан, Вайоминг (2014), «Треугольные диски Рело: новая форма на блоке», Журнал Американского химического общества , 136 (37): 12840–12843, doi : 10.1021/ja506625y , PMID   25072943 .
  69. ^ Банчофф, Томас; Гиблин, Питер (1994), «О геометрии кусочно-круговых кривых», American Mathematical Monthly , 101 (5): 403–416, doi : 10.2307/2974900 , JSTOR   2974900 , MR   1272938 .
  70. ^ Вебер, Кристоф (2009). Какое отношение это тело имеет к шару? (PDF) У Вебера также есть фильмы, демонстрирующие вращение тела Мейснера обоих типов, а также интерактивные изображения .
  71. ^ Кампи, Стефано; Колезанти, Андреа; Гронки, Паоло (1996), «Задачи минимума для объемов выпуклых тел», Уравнения в частных производных и их приложения: Сборник статей в честь Карло Пуччи , Конспекты лекций по чистой и прикладной математике, вып. 177, Марсель Деккер, стр. 43–55 .
  72. ^ Чандру, В.; Венкатараман, Р. (1991), «Круглые оболочки и орбиформы простых многоугольников» , Труды второго ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (SODA '91) , Филадельфия, Пенсильвания, США: Общество промышленной и прикладной математики, стр. . 433–440, ISBN.  978-0-89791-376-8 .
  73. ^ Петерсон, Брюс Б. (1973), «Свойства пересечения кривых постоянной ширины» , Illinois Journal of Mathematics , 17 (3): 411–420, doi : 10.1215/ijm/1256051608 , MR   0320885 .
  74. ^ Эрнандес Сифре, Массачусетс (2000), «Существует ли плоское выпуклое множество с заданной шириной, диаметром и радиусом?», American Mathematical Monthly , 107 (10): 893–900, doi : 10.2307/2695582 , JSTOR   2695582 , MR   1806918 .
  75. ^ Линдстрем, Бернт; Зеттерстрем, Ханс-Олов (1991), «Круги Борромео невозможны», American Mathematical Monthly , 98 (4): 340–341, doi : 10.2307/2323803 , JSTOR   2323803 .
  76. ^ Вайсштейн, Эрик В. , «Трикетра» , MathWorld
  77. ^ Привет, Джессика; Миллетт, Кеннет К. (2014), «Математический анализ завязывания и связывания в картеле Винчианской академии Леонардо да Винчи» (PDF) , Журнал математики и искусств .
  78. ^ Курант, Ричард ; Роббинс, Герберт (1996), Что такое математика? Элементарный подход к идеям и методам (2-е изд.), Oxford University Press, стр. 378–379, ISBN  978-0-19-975487-8 .
  79. ^ Локвуд, Э.Х. (1961), «Глава 8: Дельтовидная мышца», Книга кривых , издательство Кембриджского университета.
  80. ^ Маккей, Дж. С. (февраль 1884 г.), «Нож сапожника», Труды Эдинбургского математического общества , 3 : 2, doi : 10.1017/s0013091500037196 .
  81. ^ Брюйнс, Дж. (1998), «Квадратичные треугольники Безье как примитивы рисования», Труды семинара ACM SIGGRAPH/EUROGRAPHICS по графическому оборудованию (HWWS '98) , Нью-Йорк, Нью-Йорк, США: ACM, стр. 15–24, doi : 10.1145/285305.285307 , ISBN  978-1-58113-097-3 , S2CID   28967106 .
  82. ^ Веннингер, Магнус Дж. (2014), Сферические модели , Дувр, с. 134, ISBN  978-0-486-14365-1 .
[ редактировать ]
Викискладе есть медиафайлы по теме треугольников Рело .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Reuleaux_triangle&oldid=1234893900#Reuleaux_polygons"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: 14689bae6d0b67a7c84d8c86fb5ace11__1721141460
URL1:https://arc.ask3.ru/arc/aa/14/11/14689bae6d0b67a7c84d8c86fb5ace11.html
Заголовок, (Title) документа по адресу, URL1:
Reuleaux triangle - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)