Пятимерное пространство

Эта статья о математических пространствах, имеющих пять измерений. Чтобы узнать о музыкальной группе, см. «5-е измерение» . Чтобы узнать об альтернативных планах существования в художественной литературе, см. Четвертое измерение в литературе .

Двумерная ортогональная проекция . 5-куба

Пятимерное пространство — это пространство с пятью измерениями . В математике последовательность N N чисел может представлять местоположение в - мерном пространстве . Если интерпретировать физически, это на одно больше, чем обычные три пространственных измерения и четвертое измерение времени, используемые в релятивистской физике .

Физика

Большая часть ранних работ по пятимерному пространству была направлена ​​на разработку теории, объединяющей четыре фундаментальных взаимодействия в природе: сильные и слабые ядерные силы, гравитацию и электромагнетизм . Немецкий математик Теодор Калуца ​​и шведский физик Оскар Кляйн независимо друг от друга разработали теорию Калуцы-Клейна в 1921 году, которая использовала пятое измерение для объединения гравитации с электромагнитной силой . Хотя позже их подходы были признаны по крайней мере частично неточными, эта концепция послужила основой для дальнейших исследований в течение прошлого столетия.

Чтобы объяснить, почему это измерение нельзя наблюдать напрямую, Кляйн предположил, что пятое измерение должно быть свернуто в крошечную компактную петлю порядка 10 ^-33 сантиметры. Согласно своим рассуждениям, он представлял свет как возмущение, вызванное рябью в высшем измерении, находящемся за пределами человеческого восприятия, подобно тому, как рыба в пруду может видеть только тени ряби на поверхности воды, вызванной каплями дождя. Хотя это и невозможно обнаружить, это косвенно подразумевает связь между, казалось бы, несвязанными силами. Теория Калуцы-Клейна пережила возрождение в 1970-х годах в связи с появлением теории суперструн и супергравитации : концепции, согласно которой реальность состоит из вибрирующих нитей энергии, постулата, математически жизнеспособного только в десяти и более измерениях. Теория суперструн затем превратилась в более обобщенный подход, известный как М-теория . М-теория предполагала потенциально наблюдаемое дополнительное измерение в дополнение к десяти основным измерениям, которые допускали существование суперструн. Остальные 10 измерений уплотнены или «свернуты» до размеров ниже субатомного уровня. Теория Калуцы-Клейна сегодня рассматривается, по сути, как калибровочная теория , где калибровкой является группа кругов .

Пятое измерение сложно наблюдать напрямую, хотя Большой адронный коллайдер дает возможность зафиксировать косвенные доказательства его существования. Физики предполагают, что столкновения субатомных частиц, в свою очередь, порождают новые частицы в результате столкновения, в том числе гравитон , который вырывается из четвертого измерения, или брану , утекающую в пятимерную массу. М-теория объяснила бы слабость гравитации по сравнению с другими фундаментальными силами природы, как можно видеть, например, при использовании магнита, чтобы поднять булавку со стола: магнит с легкостью преодолевает гравитационное притяжение всей Земли. .

В начале 20 века были разработаны математические подходы, которые рассматривали пятое измерение как теоретическую конструкцию. Эти теории ссылаются на гильбертово пространство , концепцию, которая постулирует бесконечное количество математических измерений, допускающих безграничное количество квантовых состояний. Эйнштейн , Бергманн и Баргман позже попытались расширить четырехмерное пространство-время до общей теории относительности дополнительного физического измерения, чтобы включить в него электромагнетизм, но им это не удалось. В своей статье 1938 года Эйнштейн и Бергман были одними из первых, кто представил современную точку зрения, согласно которой четырехмерная теория, которая совпадает с теорией Эйнштейна – Максвелла на больших расстояниях, выводится из пятимерной теории с полной симметрией во всех пяти измерениях. . Они предположили, что электромагнетизм возникает из-за гравитационного поля, «поляризованного» в пятом измерении.

Главной новизной Эйнштейна и Бергмана было серьезное рассмотрение пятого измерения как физической сущности, а не повода для объединения метрического тензора и электромагнитного потенциала. Но затем они изменили теорию, нарушив ее пятимерную симметрию. Их рассуждения, как предложил Эдвард Виттен , заключались в том, что более симметричная версия теории предсказывала существование нового дальнодействующего поля, одновременно безмассового и скалярного , что потребовало бы фундаментальной модификации общей теории относительности Эйнштейна . Пространство Минковского и уравнения Максвелла в вакууме можно вложить в пятимерный тензор кривизны Римана .

В 1993 году физик Жерар 'т Хоофт выдвинул голографический принцип , который объясняет, что информация о дополнительном измерении видна как искривление пространства-времени, в котором на одно измерение меньше . Например, голограммы — это трехмерные изображения, размещенные на двухмерной поверхности, что придает изображению кривизну при движении наблюдателя. Точно так же в общей теории относительности четвертое измерение проявляется в наблюдаемых трех измерениях как кривизна траектории движущейся бесконечно малой (пробной) частицы. 'Т Хоофт предположил, что пятое измерение на самом деле представляет собой «ткань пространства-времени».

Недавние исследования предлагают несколько альтернативных интерпретаций пятимерного расширения пространства-времени , большинство из которых обобщают более раннюю теорию Калуцы-Клейна . Первый подход — это пространство-время-материя , который использует неограниченную группу преобразований 5D-координат для получения новых решений уравнений поля Эйнштейна, которые согласуются с соответствующими классическими решениями в 4D-пространстве-времени. Другое пятимерное представление описывает квантовую физику с точки зрения ансамбля теплового пространства-времени и устанавливает связи с классической теорией поля как предельными случаями. Еще один подход, представление пространства-киме, поднимает обычное время от положительно-действительного числа с упорядочением событий до комплексного времени (киме), что эффективно преобразует продольные процессы из временных рядов в двумерные многообразия (киме-поверхности).

Пятимерная геометрия

Согласно определению Кляйна, «геометрия — это изучение инвариантных свойств пространства-времени при преобразованиях внутри него самого». Поэтому геометрия 5-го измерения изучает инвариантные свойства такого пространства-времени по мере нашего движения внутри него, выраженные в формальных уравнениях. Пятимерная геометрия обычно представляется с использованием пяти значений координат (x,y,z,w,v), где перемещение по оси v предполагает перемещение между различными гиперобъемами .

Многогранники

Основная статья: 5-многогранник

В пяти и более измерениях только три правильных многогранника существуют . В пяти измерениях это:

1. семейства 5-симплекс симплексов { 3,3,3,3} с 6 вершинами, 15 ребрами, 20 гранями (каждая равносторонний треугольник ), 15 ячейками (каждая представляет собой правильный тетраэдр ) и 6 гиперячейками (каждая представляет собой правильный тетраэдр). 5-клеточный ).
2. семейства 5-куб гиперкубов { 4,3,3,3} с 32 вершинами, 80 ребрами, 80 гранями (каждая квадрат ), 40 ячейками (каждая куб ) и 10 гиперячейками (каждая тессеракт ). .
3. 5 -ортоплекс семейства перекрестных многогранников {3,3,3,4} с 10 вершинами, 40 ребрами, 80 гранями (каждая треугольник ), 80 ячейками (каждая тетраэдр ) и 32 гиперячейками (каждая 5 -клетка ).

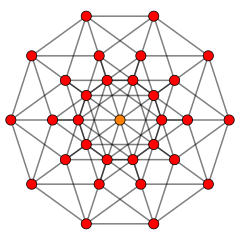
Важным однородным 5-многогранником является 5-демикуб , h{4,3,3,3} имеет половину вершин 5-куба (16), ограниченных чередующимися 5-ячеечными и 16-ячеечными гиперячейками. Расширенный — или стерилизованный 5-симплекс это вершинная фигура А ₅ решетки , . Он имеет двойную симметрию по сравнению с симметричной диаграммой Кокстера. Поцелуйное число решетки 30 представлено в ее вершинах. Выпрямленный 5-ортоплекс — это вершинная фигура D ₅ решетки , . Ее 40 вершин представляют собой число поцелуев решетки и самое высокое для измерения 5.

Правильные и полуправильные многогранники в пяти измерениях.
(Отображается в виде ортогональных проекций в каждой Кокстера плоскости симметрии )

AА5	Авто(А 5 )	Б 5			Д 5
5-симплекс {3,3,3,3}	Стерический 5-симплекс	5-куб {4,3,3,3}	5-ортоплекс {3,3,3,4}	Выпрямленный 5-ортоплекс г {3,3,3,4}	5-демикуб ч{4,3,3,3}

Гиперсфера

Гиперсфера , поскольку ее в 5-мерном пространстве (также называемая 4-сферой поверхность четырехмерна) состоит из набора всех точек в 5-мерном пространстве, находящихся на фиксированном расстоянии r от центральной точки P, что является вращательно-симметричным . Гиперобъем, заключенный в эту гиперповерхность, равен:

$V={\frac {8\pi ^{2}r^{5}}{15}}$

См. также

• 5-многообразие
• Гравитация
• Гиперсфера
• Список правильных 5-многогранников
• Четырехмерное пространство

Дальнейшее чтение

• Вессон, Пол С. (1999). Пространство-время-материя, современная теория Калуцы-Клейна . Сингапур: World Scientific. ISBN  981-02-3588-7 .
• Вессон, Пол С. (2006). Пятимерная физика: классические и квантовые следствия космологии Калуцы-Клейна . Сингапур: World Scientific. ISBN  981-256-661-9 .
• Вейль, Герман , Раум, Zeit, Materie , 1918. 5 изд. к 1922 г. изд. с примечаниями Юргена Элерса, 1980. пер. 4-е изд. Генри Броуз, 1922 г. «Пространство-Время Материя» , Метуэн, представитель. 1952 год, Дувр. ISBN   0-486-60267-2 .

Внешние ссылки

• Анаглиф пятимерного гиперкуба в гиперперспективе