Закон Меткалфа

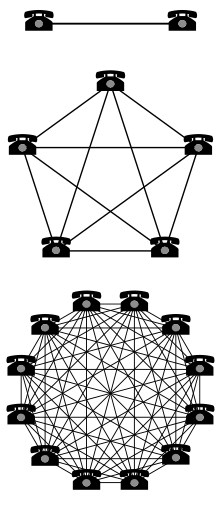
Два телефона могут установить только одно соединение , пять — 10 соединений, а двенадцать — 66 соединений.

Закон Меткалфа гласит, что финансовая ценность или влияние телекоммуникационной сети пропорциональны квадрату числа подключенных пользователей системы ( n ²). Закон назван в честь Роберта Меткалфа и впервые был предложен в 1980 году, хотя и не с точки зрения пользователей, а скорее с точки зрения «совместимых коммуникационных устройств» (например, факсов, телефонов). ^{[ 1 ]} Позже он стал ассоциироваться с пользователями Ethernet после статьи в журнале Forbes Джорджа Гилдера в сентябре 1993 года . ^{[ 2 ]}

Сетевые эффекты

Закон Меткалфа характеризует многие сетевые эффекты коммуникационных технологий и сетей, таких как Интернет , социальные сети и Всемирная паутина . США Бывший председатель Федеральной комиссии по связи Рид Хундт заявил, что этот закон дает наибольшее понимание работы современного Интернета. ^{[ 3 ]} Математически закон Меткалфа показывает, что количество уникальных возможных связей в $n$ -узловое соединение можно выразить треугольным числом $n(n-1)/2$ , что асимптотически пропорционально $n^{2}$ .

Закон часто иллюстрируется на примере факсимильных аппаратов: один факсимильный аппарат сам по себе бесполезен, но ценность каждого факсимильного аппарата возрастает с увеличением общего количества факсимильных аппаратов в сети, поскольку общее количество людей, с которыми каждый пользователь может отправлять и получать документы увеличивается. ^{[ 4 ]} Это обычная иллюстрация для объяснения сетевого эффекта . Таким образом, в любых социальных сетях, чем больше пользователей пользуется сервисом, тем ценнее сервис становится для сообщества.

История и происхождение

Закон Меткалфа был задуман в 1983 году в ходе презентации для отдела продаж 3Com . ^{[ 5 ]} В нем говорилось, что V будет пропорционально общему количеству возможных соединений или примерно n -квадрату.

В первоначальном воплощении было тщательно разграничено линейные затраты ( Cn ) и нелинейный рост ( n ²) и непостоянную близость коэффициента пропорциональности ( A ). Точка безубыточности , при которой затраты окупаются, определяется по формуле: $C\times n=A\times n(n-1)/2$ При некотором размере правая часть уравнения V , стоимость, превышает затраты, а A описывает взаимосвязь между размером и чистой добавленной стоимостью. Тогда для больших n чистая стоимость сети составит: $\Pi =n(A\times (n-1)/2-C)$ Меткалф правильно определил размер А как «ценность на пользователя». Сродство также является функцией размера сети, и Меткалф правильно предположил, что A должно уменьшаться по мере n увеличения . В интервью 2006 года Меткалф заявил: ^{[ 6 ]}

Масштаб сети может привести к негативным последствиям, которые в конечном итоге приводят к снижению стоимости с увеличением размера. Итак, если V=A*n ², возможно, что A (для «близости», значения на соединение) также является функцией n и направляется вниз после некоторого размера сети, подавляя n ².

Рост `n`

Размер сети и, следовательно, ее ценность не растут беспредельно, а ограничиваются практическими ограничениями, такими как инфраструктура, доступ к технологиям и ограниченной рациональностью, такой как число Данбара . Почти всегда рост числа пользователей n достигает точки насыщения. Технологии, заменители, конкуренты и техническое устаревание сдерживают рост n . Обычно предполагается, что рост n следует сигмовидной функции, такой как логистическая кривая или кривая Гомпертца .

Плотность

A также определяется связностью или плотностью топологии сети. В неориентированной сети каждое ребро соединяет два узла, так что на каждое ребро приходится 2 m узлов. Доля узлов, находящихся в фактическом контакте, определяется выражением $c=2m/n$ .

Максимально возможное количество ребер в простой сети (т. е. в сети без мультиребер и саморебер) равно ${\binom {n}{2}}=n(n-1)/2$ . Следовательно, плотность сети ρ — это доля реально присутствующих ребер:

\rho =c/(n-1)

что для больших сетей аппроксимируется выражением $\rho =c/n$ . ^{[ 7 ]}

Ограничения

Закон Меткалфа предполагает, что значение каждого узла $n$ приносит равную пользу. ^{[ 3 ]} Если это не так, например, если один факсимильный аппарат обслуживает 60 работников компании, второй факсимильный аппарат обслуживает половину этого числа, третий – треть и т. д., то относительная ценность дополнительного соединения уменьшается. Аналогичным образом, в социальных сетях, если пользователи, которые присоединяются позже, используют сеть меньше, чем первые пользователи, тогда выгода от каждого дополнительного пользователя может уменьшиться, что делает сеть в целом менее эффективной, если затраты на одного пользователя фиксированы.

Модифицированные модели

В контексте социальных сетей многие, в том числе и сам Меткалф, предлагали модифицированные модели, в которых ценность сети растет по мере увеличения количества социальных сетей. $n\log n$ скорее, чем $n^{2}$ . ^{[ 8 ]}^{[ 3 ]} Рид ^{[ не следует ]} и Эндрю Одлызко искали возможные связи с законом Меткалфа с точки зрения описания отношений в сети, и можно прочитать о том, как они связаны. Тонджиа и Уилсон также изучают связанный с этим вопрос о издержках для тех, кто исключен. ^{[ 9 ]}

Проверка данных

На протяжении более 30 лет было мало конкретных доказательств в поддержку закона. Наконец, в июле 2013 года голландские исследователи проанализировали модели использования Интернета в Европе за достаточно длительный период времени. ^{[ указать ]} и нашел $n^{2}$ пропорциональность для малых значений $n$ и $n\log n$ пропорциональность для больших значений $n$ . ^{[ 10 ]} Несколько месяцев спустя сам Меткалф предоставил дополнительные доказательства, используя данные Facebook за последние 10 лет, чтобы показать хорошее соответствие закону Меткалфа. ^{[ 11 ]}

В 2015 году Чжан, Лю и Сюй параметризовали функцию Меткалфа на основе данных Tencent и Facebook. Их работа показала, что закон Меткалфа справедлив для обоих сайтов, несмотря на различия в аудитории между двумя сайтами (Facebook обслуживает аудиторию по всему миру, а Tencent обслуживает только китайских пользователей). Функции для двух сайтов были $V_{Tencent}=7.39\times 10^{-9}\times n^{2}$ и $V_{Facebook}=5.70\times 10^{-9}\times n^{2}$ соответственно. ^{[ 12 ]} Одно из первых упоминаний закона Меткалфа в контексте Биткойна было в сообщении Сантостази на Reddit в 2014 году. Он сравнил наблюдаемое обобщенное поведение Меткалфа для Биткойна с законом Ципфа и теоретическим результатом Меткалфа. ^{[ 13 ]} Закон Меткалфа является важнейшим компонентом теории энергетического закона Биткойна Сантостази. ^{[ 14 ]} В рабочем документе Петерсон связал концепции временной стоимости денег со стоимостью Меткалфа, используя Биткойн и Facebook в качестве числовых примеров доказательства: ^{[ 15 ]} а в 2018 году применил закон Меткалфа к Биткойну , показав, что более 70% отклонений в стоимости Биткойна объясняются применением закона Меткалфа к увеличению размера сети Биткойн. ^{[ 16 ]}

В интервью 2024 года математик Терренс Тао подчеркнул важность универсальности и сетевых связей внутри математического сообщества, для чего он сослался на закон Меткалфа. Тао считает, что более широкая аудитория приводит к большему количеству связей, что в конечном итоге приводит к положительным изменениям внутри сообщества. Для этого он процитировал закон Меткалфа, подтверждающий эту точку зрения. Далее Тао заявил: «Вся моя карьера заключалась в том, что чем больше связей, тем лучше происходит». ^{[ 17 ]}

См. также

Ссылки

^ Симеонов, Симеон (26 июля 2006 г.). «Закон Меткалфа: скорее неправильно понят, чем ошибочен?» . HighContrast: Инновации и венчурный капитал в эпоху после широкополосной связи .
^ Шапиро, Карл; Вариан, Хэл Р. (1999). Информационные правила . Гарвардская деловая пресса. ISBN 9780875848631 .
^ Jump up to: ^а ^б ^с Бриско, Боб; Одлыжко, Андрей ; Тилли, Бенджамин (июль 2006 г.). «Закон Меткалфа неверен» . IEEE-спектр . 43 (7): 34–39. дои : 10.1109/MSPEC.2006.1653003 . S2CID 45462851 . Проверено 15 сентября 2022 г.
^ Тонгия, Рахул; Уилсон, Э.Дж. (8 апреля 2011 г.). «Теория сетей | Обратная сторона закона Меткалфа: множественные и растущие издержки исключения сети». Международный журнал коммуникации . S2CID 153848093 .
^ Меткалф, Боб (декабрь 2013 г.). «Закон Меткалфа после 40 лет Ethernet» . Компьютер . 46 (12): 26–31. дои : 10.1109/MC.2013.374 . ISSN 1558-0814 . S2CID 206448593 .
^ Меткалф, Роберт (18 августа 2006 г.). «Приглашенный блоггер Боб Меткалф: Закон Меткалфа повторяется в длинном хвосте социальных сетей» . Блог VC Майка .
^ Ньюман, Марк Э.Дж. (2019). «Математика сетей» в разделе «Сети» . Издательство Оксфордского университета. стр. 126–128. ISBN 9780198805090 .
^ «Приглашенный блоггер Боб Меткалф: Закон Меткалфа повторяется в длинном хвосте социальных сетей» . 18 августа 2006 г. Проверено 20 июня 2010 г.
^ Тонгия, Рахул; Уилсон, Эрнест (сентябрь 2007 г.). «Обратная сторона закона Меткалфа: многочисленные и растущие издержки исключения сети» . Международный журнал коммуникации . 5:17 . Проверено 15 января 2013 г.
^ Мадурейра, Антониу; ден Хартог, Фрэнк; Бауман, Гарри ; Бакен, Нико (2013). «Эмпирическое подтверждение закона Меткалфа: как со временем изменились модели использования Интернета». Информационная экономика и политика . 25 (4): 246–256. doi : 10.1016/j.infoecopol.2013.07.002 .
^ Меткалф, Боб (2013). «Закон Меткалфа после 40 лет Ethernet». IEEE-компьютер . 46 (12): 26–31. дои : 10.1109/MC.2013.374 . S2CID 206448593 .
^ Чжан, Син-Чжоу; Лю, Цзин-Цзе; Сюй, Чжи-Вэй (2015). «Данные Tencent и Facebook подтверждают закон Меткалфа». Журнал компьютерных наук и технологий . 30 (2): 246–251. дои : 10.1007/s11390-015-1518-1 . S2CID 255158958 .
^ «Биткойн в сравнении с законом Меткалфа и Ципфа» . 29 марта 2014 года . Проверено 29 марта 2014 г.
^ «Теория энергетического закона Биткойна» . 20 марта 2024 г. Проверено 20 марта 2024 г.
^ Петерсон, Тимоти (2019). «Биткойн распространяется как вирус». Рабочий документ . дои : 10.2139/ssrn.3356098 . S2CID 159240517 .
^ Петерсон, Тимоти (2018). «Закон Меткалфа как модель стоимости биткойнов». Обзор альтернативных инвестиционных аналитиков . 7 (2): 9–18. дои : 10.2139/ssrn.3078248 . S2CID 158572041 .
^ Строгац, Стивен (1 февраля 2024 г.). «Что делает математику хорошей?» . Журнал Кванта .

Дальнейшее чтение

Смит, Дэвид; Скелли, Калифорния (лето 2006 г.). «Трансформация глобализации» (PDF) . Деловой журнал Теннесси . стр. 17–19.

Внешние ссылки

Группа – злейший враг самой себе . Программная речь Клея Ширки о социальном программном обеспечении на конференции O'Reilly Emerging Technology, Санта-Клара, 24 апреля 2003 г. Четвертая из его «Четырех вещей, ради которых нужно проектировать»: «И, наконец, вам нужно найти способ сэкономить группа из-за масштаба. Масштаб сам по себе убивает разговоры, потому что разговоры требуют плотных двусторонних разговоров. В разговорном контексте закон Меткалфа является тормозом».

[1] Симеонов, Симеон (26 июля 2006 г.). «Закон Меткалфа: скорее неправильно понят, чем ошибочен?» . HighContrast: Инновации и венчурный капитал в эпоху после широкополосной связи .

[2] Шапиро, Карл; Вариан, Хэл Р. (1999). Информационные правила . Гарвардская деловая пресса. ISBN 9780875848631 .

[Briscoe_Odlyzko_Tilly-3] Jump up to: ^а ^б ^с Бриско, Боб; Одлыжко, Андрей ; Тилли, Бенджамин (июль 2006 г.). «Закон Меткалфа неверен» . IEEE-спектр . 43 (7): 34–39. дои : 10.1109/MSPEC.2006.1653003 . S2CID 45462851 . Проверено 15 сентября 2022 г.

[4] Тонгия, Рахул; Уилсон, Э.Дж. (8 апреля 2011 г.). «Теория сетей | Обратная сторона закона Меткалфа: множественные и растущие издержки исключения сети». Международный журнал коммуникации . S2CID 153848093 .

[5] Меткалф, Боб (декабрь 2013 г.). «Закон Меткалфа после 40 лет Ethernet» . Компьютер . 46 (12): 26–31. дои : 10.1109/MC.2013.374 . ISSN 1558-0814 . S2CID 206448593 .

[6] Меткалф, Роберт (18 августа 2006 г.). «Приглашенный блоггер Боб Меткалф: Закон Меткалфа повторяется в длинном хвосте социальных сетей» . Блог VC Майка .

[7] Ньюман, Марк Э.Дж. (2019). «Математика сетей» в разделе «Сети» . Издательство Оксфордского университета. стр. 126–128. ISBN 9780198805090 .

[8] «Приглашенный блоггер Боб Меткалф: Закон Меткалфа повторяется в длинном хвосте социальных сетей» . 18 августа 2006 г. Проверено 20 июня 2010 г.

[9] Тонгия, Рахул; Уилсон, Эрнест (сентябрь 2007 г.). «Обратная сторона закона Меткалфа: многочисленные и растущие издержки исключения сети» . Международный журнал коммуникации . 5:17 . Проверено 15 января 2013 г.

[10] Мадурейра, Антониу; ден Хартог, Фрэнк; Бауман, Гарри ; Бакен, Нико (2013). «Эмпирическое подтверждение закона Меткалфа: как со временем изменились модели использования Интернета». Информационная экономика и политика . 25 (4): 246–256. doi : 10.1016/j.infoecopol.2013.07.002 .

[11] Меткалф, Боб (2013). «Закон Меткалфа после 40 лет Ethernet». IEEE-компьютер . 46 (12): 26–31. дои : 10.1109/MC.2013.374 . S2CID 206448593 .

[12] Чжан, Син-Чжоу; Лю, Цзин-Цзе; Сюй, Чжи-Вэй (2015). «Данные Tencent и Facebook подтверждают закон Меткалфа». Журнал компьютерных наук и технологий . 30 (2): 246–251. дои : 10.1007/s11390-015-1518-1 . S2CID 255158958 .

[13] «Биткойн в сравнении с законом Меткалфа и Ципфа» . 29 марта 2014 года . Проверено 29 марта 2014 г.

[14] «Теория энергетического закона Биткойна» . 20 марта 2024 г. Проверено 20 марта 2024 г.

[15] Петерсон, Тимоти (2019). «Биткойн распространяется как вирус». Рабочий документ . дои : 10.2139/ssrn.3356098 . S2CID 159240517 .

[16] Петерсон, Тимоти (2018). «Закон Меткалфа как модель стоимости биткойнов». Обзор альтернативных инвестиционных аналитиков . 7 (2): 9–18. дои : 10.2139/ssrn.3078248 . S2CID 158572041 .

[17] Строгац, Стивен (1 февраля 2024 г.). «Что делает математику хорошей?» . Журнал Кванта .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

v т и Социальные сети и социальные сети
Types	Personal Professional Sexual Value Clique Adolescent
Networks	Corporate social media Distributed social network (list) Enterprise social networking Enterprise social software Mobile social network Personal knowledge networking
Services	List of social networking services List of virtual communities with more than 1 million users
Concepts and theories	Ambient awareness Assortative mixing Attention inequality Interpersonal bridge Organizational network analysis Small-world experiment Social aspects of television Social capital Social data revolution Social exchange theory Social identity theory Social media and psychology Social media intelligence Social media mining Social media optimization Social network analysis Social web Structural endogamy Virtual collective consciousness
Models and processes	Account verification Aggregation Change detection Blockmodeling Collaboration graph Collaborative consumption Giant Global Graph Lateral communication Reputation system Social bot Social graph Social media analytics Social network analysis software Social networking potential Social television Structural cohesion
Economics	Affinity fraud Attention economy Collaborative finance Creator economy Influencer marketing Narrowcasting Sharing economy Social commerce Social sorting Viral marketing
Phenomena	Algorithmic radicalization Community recognition Complex contagion Computer addiction Consequential strangers Friend of a friend Friending and following Friendship paradox Influence-for-hire Internet addiction Information overload Overchoice Six degrees of separation Social media addiction Social media and suicide Social invisibility Social network game Suicide and the Internet Tribe Viral phenomenon
Related topics	Friendship recession Peer pressure Researchers User profile Online identity Persona Social profiling Viral messages Virtual community