Исследовательский анализ данных
| Часть серии по статистике. |
| Визуализация данных и информации |
|---|
| Основные размеры |
| Важные цифры |
| Информационные графические типы |
|
| Связанные темы |
В статистике исследовательский анализ данных (EDA) — это подход к анализу наборов данных для обобщения их основных характеристик, часто с использованием статистической графики и других методов визуализации данных . Статистическая модель может использоваться или нет, но в первую очередь EDA предназначена для того, чтобы увидеть, что данные могут сказать нам за пределами формального моделирования, и тем самым контрастирует с традиционной проверкой гипотез. Исследовательский анализ данных продвигался Джоном Тьюки с 1970 года, чтобы побудить статистиков исследовать данные и, возможно, сформулировать гипотезы, которые могли бы привести к сбору новых данных и экспериментам. EDA отличается от анализа исходных данных (IDA) , [1] [2] который более узко фокусируется на проверке предположений, необходимых для подбора модели и проверки гипотез, а также на обработке пропущенных значений и преобразовании переменных по мере необходимости. EDA включает в себя IDA.
Обзор
[ редактировать ]Тьюки определил анализ данных в 1961 году как: «Процедуры анализа данных, методы интерпретации результатов таких процедур, способы планирования сбора данных, чтобы сделать их анализ проще, точнее или точнее, а также все механизмы и результаты ( математическая) статистика, которая применяется для анализа данных». [3]
Исследовательский анализ данных — это метод анализа, позволяющий анализировать и исследовать набор данных и суммировать основные характеристики набора данных. Основным преимуществом EDA является обеспечение визуализации данных после проведения анализа.
Поддержка Тьюки EDA способствовала разработке пакетов статистических вычислений , особенно S в Bell Labs . [4] вдохновил системы S-PLUS и R. Язык программирования S Это семейство статистических вычислительных сред отличалось значительно улучшенными возможностями динамической визуализации, что позволило статистикам выявлять выбросы , тенденции и закономерности в данных, заслуживающие дальнейшего изучения.
EDA Тьюки была связана с двумя другими достижениями в статистической теории : устойчивой статистикой и непараметрической статистикой , обе из которых пытались уменьшить чувствительность статистических выводов к ошибкам в формулировании статистических моделей . Тьюки пропагандировал использование пятизначной сводки числовых данных — двух крайних значений ( максимального и минимального ), медианы и квартилей — поскольку эти медиана и квартили, являющиеся функциями эмпирического распределения , определены для всех распределений, в отличие от среднего и квартилей. стандартное отклонение ; более того, квартили и медиана более устойчивы к асимметричному распределению или распределению с тяжелым хвостом , чем традиционные сводные данные (среднее и стандартное отклонение). Пакеты S , S-PLUS и R использующие статистику передискретизации Кенуя и Тьюки , такие как складной нож и Эфрона включали процедуры , бутстрап , которые являются непараметрическими и устойчивыми (для многих задач).
Исследовательский анализ данных, надежная статистика, непараметрическая статистика и развитие языков статистического программирования облегчили работу статистиков над научными и инженерными проблемами. К таким проблемам относились производство полупроводников и понимание сетей связи, которые касались Bell Labs. Эти статистические разработки, все поддержанные Тьюки, были разработаны, чтобы дополнить аналитическую теорию проверки статистических гипотез , особенно акцент лапласовской традиции на экспоненциальных семействах . [5]
Разработка
[ редактировать ]
Джон В. Тьюки написал книгу «Исследовательский анализ данных» в 1977 году. [6] Тьюки считал, что слишком много внимания в статистике уделяется проверке статистических гипотез (анализу подтверждающих данных); больше внимания необходимо уделять использованию данных для выдвижения гипотез для проверки. В частности, он считал, что смешение двух типов анализа и их использование на одном и том же наборе данных может привести к систематической ошибке из-за проблем, присущих проверке гипотез, предложенных данными .
Целями EDA являются:
- Включите неожиданные открытия в данных
- Выдвинуть гипотезы о причинах наблюдаемых явлений.
- Оцените предположения, на которых статистические выводы. будут основаны
- Поддержка выбора соответствующих статистических инструментов и методов.
- Обеспечить основу для дальнейшего сбора данных посредством опросов или экспериментов. [7]
Многие методы EDA были внедрены в интеллектуальный анализ данных . Им также обучают молодых студентов, чтобы познакомить их со статистическим мышлением. [8]
Техники и инструменты
[ редактировать ]Существует ряд инструментов, полезных для EDA, но EDA характеризуется скорее отношением, чем конкретными методами. [9]
Типичными графическими методами, используемыми в EDA, являются:
- Коробочный сюжет
- Гистограмма
- Многовариантная диаграмма
- График запуска
- Диаграмма Парето
- График рассеяния (2D/3D)
- Участок стебля и листьев
- Параллельные координаты
- Коэффициент шансов
- Целенаправленное проецирование
- Тепловая карта
- Гистограмма
- График горизонта
- Методы визуализации на основе глифов, такие как PhenoPlot. [10] и лица Чернова
- Методы проекции, такие как большой тур, экскурсия с гидом и экскурсия вручную.
- Интерактивные версии этих сюжетов
- Многомерное масштабирование
- Анализ главных компонентов (PCA)
- Мультилинейный PCA
- Нелинейное уменьшение размерности (NLDR)
- Иконография корреляций
Типичными количественными методами являются:
История
[ редактировать ]Многие идеи EDA восходят к более ранним авторам, например:
- Фрэнсис Гальтон уделял особое внимание порядковой статистике и квантилям .
- Артур Лайон Боули использовал предшественники основного графика и пятизначную сводку (Боули фактически использовал « семизначную сводку », включая крайние значения, децили и квартили , а также медиану — см. его «Элементарное руководство по статистике» (3-е изд., 1920 г.) ), стр. 62 [11] – он определяет «максимум и минимум, медиану, квартиль и два дециля» как «семь позиций»).
- Эндрю Эренберг сформулировал философию сокращения данных (см. его одноименную книгу).
Курс Открытого университета « Статистика в обществе» (MDST 242) взял вышеизложенные идеи и объединил их с Готфрида Нётера работой , которая представила статистические выводы посредством подбрасывания монеты и медианного теста .
Пример
[ редактировать ]Результаты EDA ортогональны задаче первичного анализа. Для иллюстрации рассмотрим пример Cook et al. где задача анализа состоит в том, чтобы найти переменные, которые лучше всего предсказывают чаевые, которые посетитель даст официанту. [12] В данных, собранных для этой задачи, доступны следующие переменные: сумма чаевых, общая сумма счета, пол плательщика, зона для курящих/некурящих, время суток, день недели и размер вечеринки. Задача первичного анализа решается путем подбора регрессионной модели, в которой ставка чаевых является переменной отклика. Подогнанная модель
- ( размер чаевых ) = 0,18–0,01 × (размер вечеринки)
В нем говорится, что по мере увеличения размера обеда на одного человека (что приводит к увеличению счета) ставка чаевых уменьшится в среднем на 1%.
Однако изучение данных выявило и другие интересные особенности, не описанные этой моделью.
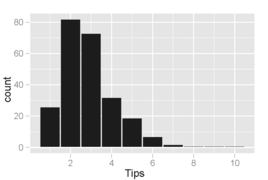
- Гистограмма сумм чаевых, где ячейки покрывают приращения в 1 доллар. Распределение значений искажено вправо и унимодально, как это часто бывает при распределениях небольших неотрицательных величин.
- Гистограмма сумм чаевых, где ячейки покрывают приращения в 0,10 доллара. Наблюдается интересный феномен: пики возникают при суммах в целые доллары и в полдоллара, что связано с тем, что клиенты выбирают в качестве чаевых круглые числа. Такое поведение характерно и для других типов покупок, например бензина.
- Диаграмма рассеяния чаевых и счета. Точки под линией соответствуют чаевым, которые ниже ожидаемых (для данной суммы счета), а точки над линией — выше ожидаемых. Мы могли бы ожидать увидеть тесную положительную линейную связь, но вместо этого видим вариацию, которая увеличивается с увеличением суммы чаевых . В частности, в правом нижнем углу больше точек, чем в левом верхнем углу, что указывает на то, что больше клиентов являются очень дешевыми, чем очень щедрыми.
- Диаграмма разброса чаевых и суммы счета с разделением по полу плательщика и статусу секции для курящих. Курящие вечеринки имеют гораздо больше разнообразия в чаевых, которые они дают. Мужчины, как правило, платят (несколько) более высокие счета, а некурящие женщины, как правило, очень регулярно дают чаевые (за тремя заметными исключениями, показанными в выборке).
То, что мы узнаем из графиков, отличается от того, что иллюстрирует регрессионная модель, хотя эксперимент не был предназначен для изучения каких-либо других тенденций. Закономерности, обнаруженные в результате изучения данных, позволяют предположить гипотезы о чаевых, которые, возможно, не были предвидены заранее, и которые могут привести к интересным последующим экспериментам, в которых гипотезы формально формулируются и проверяются путем сбора новых данных.
Программное обеспечение
[ редактировать ]- JMP , пакет EDA от Института SAS .
- KNIME , Konstanz Information Miner — платформа для исследования данных с открытым исходным кодом, основанная на Eclipse.
- Minitab — пакет EDA и общей статистики, широко используемый в промышленных и корпоративных условиях.
- Orange — с открытым исходным кодом пакет программного обеспечения для анализа данных и машинного обучения .
- Python — язык программирования с открытым исходным кодом, широко используемый в интеллектуальном анализе данных и машинном обучении.
- R — язык программирования с открытым исходным кодом для статистических вычислений и графики. Вместе с Python один из самых популярных языков для анализа данных.
- TinkerPlots — программное обеспечение EDA для учащихся старших классов начальной и средней школы.
- Weka — пакет интеллектуального анализа данных с открытым исходным кодом, который включает в себя инструменты визуализации и EDA, такие как целевое прогнозирование .
См. также
[ редактировать ]- Квартет Анскомба о важности исследований
- Извлечение данных
- Прогнозная аналитика
- Анализ структурированных данных (статистика)
- Конфигурационный частотный анализ
- Описательная статистика
Ссылки
[ редактировать ]- ^ Чатфилд, К. (1995). Решение проблем: Руководство для статистика (2-е изд.). Чепмен и Холл. ISBN 978-0412606304 .
- ^ Бэйли, Марк; Ле Сесси, Саския; Шмидт, Карстен Оливер; Луса, Лара; Хюбнер, Марианна; Тематическая группа «Анализ исходных данных» инициативы STRATOS (2022 г.). «Десять простых правил первичного анализа данных» . PLOS Вычислительная биология . 18 (2): e1009819. Бибкод : 2022PLSCB..18E9819B . дои : 10.1371/journal.pcbi.1009819 . ПМЦ 8870512 . ПМИД 35202399 .
- ^ Джон Тьюки-Будущее анализа данных-июль 1961 г.
- ^ Беккер, Ричард А., Краткая история S , Мюррей Хилл, Нью-Джерси: AT&T Bell Laboratories, заархивировано из оригинала (PS) 23 июля 2015 г. , получено 23 июля 2015 г. ,
... мы хотели быть способны взаимодействовать с нашими данными, используя методы исследовательского анализа данных (Tukey, 1971).
- ^ Моргенталер, Стефан; Фернхольц, Луиза Т. (2000). «Разговор с Джоном В. Тьюки и Элизабет Тьюки, Луизой Т. Фернхольц и Стефаном Моргенталером» . Статистическая наука . 15 (1): 79–94. дои : 10.1214/ss/1009212675 .
- ^ Тьюки, Джон В. (1977). Исследовательский анализ данных . Пирсон. ISBN 978-0201076165 .
- ^ Беренс-Принципы и процедуры исследовательского анализа данных-Американская психологическая ассоциация-1997
- ^ Конольд, К. (1999). «Статистика идет в школу». Современная психология . 44 (1): 81–82. дои : 10.1037/001949 .
- ^ Тьюки, Джон В. (1980). «Нам нужны как исследовательские, так и подтверждающие». Американский статистик . 34 (1): 23–25. дои : 10.1080/00031305.1980.10482706 .
- ^ Сайлем, Хеба З.; Серо, Джулия Э.; Бакал, Крис (08 января 2015 г.). «Визуализация данных клеточной визуализации с помощью PhenoPlot» . Природные коммуникации . 6 (1): 5825. Бибкод : 2015NatCo...6.5825S . дои : 10.1038/ncomms6825 . ISSN 2041-1723 . ПМЦ 4354266 . ПМИД 25569359 .
- ^ Элементарное руководство по статистике (3-е изд., 1920 г.) https://archive.org/details/cu31924013702968/page/n5
- ^ Кук, Д. и Суэйн, Д.Ф. (совместно с А. Буджой, Д. Темпл Лэнгом, Х. Хофманном, Х. Уикхэмом, М. Лоуренсом) (2007) «Интерактивная и динамическая графика для анализа данных: с R и GGobi» Springer , 978-0387717616
Библиография
[ редактировать ]- Андриенко Н. и Андриенко Г. (2005) Исследовательский анализ пространственных и временных данных. Системный подход . Спрингер. ISBN 3-540-25994-5
- Кук, Д. и Суэйн, Д.Ф. (совместно с А. Буджой, Д. Темпл Лэнгом, Х. Хофманном, Х. Уикхэмом, М. Лоуренсом) (12 декабря 2007 г.). Интерактивная и динамическая графика для анализа данных: с помощью R и GGobi . Спрингер. ISBN 9780387717616 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - Кук, Д. и Суэйн, Д.Ф. (совместно с А. Буджой, Д. Темпл Лэнгом, Х. Хофманном, Х. Уикхэмом, М. Лоуренсом) (12 декабря 2007 г.). Интерактивная и динамическая графика для анализа данных: с помощью R и GGobi. Спрингер. ISBN 9780387717616.
- Хоглин, округ Колумбия; Мостеллер, Ф. и Тьюки, Джон Уайлдер (редакторы) (1985). Изучение таблиц данных, тенденций и фигур. ISBN 978-0-471-09776-1.
- Хоглин, округ Колумбия; Мостеллер, Ф. и Тьюки, Джон Уайлдер (редакторы) (1983). Понимание надежного и исследовательского анализа данных. ISBN 978-0-471-09777-8.
- Янг, Ф. В. Валеро-Мора, П. и Френдли М. (2006) Визуальная статистика: просмотр данных с помощью динамической интерактивной графики. Wiley ISBN 978-0-471-68160-1 Джамбу М. (1991) Исследовательский и многомерный анализ данных. ISBN Академического издательства 0123800900
- SHC DuToit, AGW Steyn, RH Stumpf (1986) Графический исследовательский анализ данных. ISBN Спрингера 978-1-4612-9371-2
- Хоглин, округ Колумбия; Мостеллер, Ф. и Тьюки, Джон Уайлдер (редакторы) (1985). Изучение таблиц данных, тенденций и фигур . Уайли. ISBN 978-0-471-09776-1 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - Хоглин, округ Колумбия; Мостеллер, Ф. и Тьюки, Джон Уайлдер (редакторы) (1983). Понимание надежного и исследовательского анализа данных . Уайли. ISBN 978-0-471-09777-8 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - Инзельберг, Альфред (2009). Параллельные координаты: визуальная многомерная геометрия и ее приложения . Лондон Нью-Йорк: Спрингер. ISBN 978-0-387-68628-8 .
- Лейнхардт Г., Лейнхардт С. Исследовательский анализ данных: новые инструменты анализа эмпирических данных , Обзор исследований в области образования, Vol. 8, 1980 (1980), стр. 85–157.
- Мартинес, WL ; Мартинес, А.Р. и Солка, Дж. (2010). Исследовательский анализ данных с помощью MATLAB, второе издание . Чепмен и Холл/CRC. ISBN 9781439812204 .
- Теус М., Урбанек С. (2008), Интерактивная графика для анализа данных: принципы и примеры, CRC Press, Бока-Ратон, Флорида, ISBN 978-1-58488-594-8
- Такер, Л; МакКаллум, Р. (1993). Исследовательский факторный анализ .
- Тьюки, Джон Уайлдер (1977). Исследовательский анализ данных . Аддисон-Уэсли. ISBN 978-0-201-07616-5 .
- Веллеман, П.Ф.; Хоглин, округ Колумбия (1981). Приложения, основы и вычисления исследовательского анализа данных . Даксбери Пресс. ISBN 978-0-87150-409-8 .
- Янг, Ф. В. Валеро-Мора, П. и Френдли М. (2006) Визуальная статистика: просмотр данных с помощью динамической интерактивной графики . Уайли ISBN 978-0-471-68160-1
- Джамбу М. (1991) Исследовательский и многомерный анализ данных . Академическая пресса ISBN 0123800900
- SHC DuToit, AGW Steyn, RH Stumpf (1986) Графический исследовательский анализ данных . Спрингер ISBN 978-1-4612-9371-2