Круговая орбита
Эта статья в значительной степени или полностью опирается на один источник . ( апрель 2020 г. ) |

| Часть серии о |
| Астродинамика |
|---|
Круговая орбита — это орбита с фиксированным расстоянием вокруг барицентра ; то есть в форме круга .При этом не только расстояние, но и скорость, угловая скорость , потенциальная и кинетическая энергия постоянны. и апоапсиса нет Периапсиса . Эта орбита не имеет радиальной версии .
Ниже перечислена круговая орбита в астродинамике или небесной механике при стандартных предположениях. Здесь центростремительная сила — это сила гравитации , а упомянутая выше ось — это линия, проходящая через центр центральной массы, перпендикулярная орбиты плоскости .
Круговое ускорение
[ редактировать ]Поперечное ускорение ( перпендикулярное скорости) вызывает изменение направления. Если оно постоянно по величине и меняет направление в зависимости от скорости, круговое движение возникает . Взяв две производные координат частицы по времени, получим центростремительное ускорение.
где:
- - орбитальная скорость вращающегося тела,
- это радиус круга
- — угловая скорость , измеряемая в радианах в единицу времени.
Формула является безразмерной и описывает соотношение, истинное для всех единиц измерения, применяемых равномерно во всей формуле. Если числовое значение измеряется в метрах на секунду в квадрате, то числовые значения будет в метрах в секунду, в метрах и в радианах в секунду.
Скорость
[ редактировать ]Скорость (или величина скорости) относительно центрального объекта постоянна: [1] : 30
где:
- , гравитационная постоянная
- , — масса обоих вращающихся тел , хотя в обычной практике, если большая масса значительно больше, меньшей массой часто пренебрегают с минимальным изменением результата.
- , — стандартный гравитационный параметр .
Уравнение движения
[ редактировать ]Уравнение орбиты в полярных координатах, которое обычно дает r через θ , сводится к: [ нужны разъяснения ] [ нужна ссылка ]
где:
- – удельный момент импульса вращающегося тела.
Это потому, что
Угловая скорость и орбитальный период
[ редактировать ]Следовательно, орбитальный период ( ) можно вычислить как: [1] : 28
Сравните две пропорциональные величины: время свободного падения (время падения до точки массы из состояния покоя).
- (17,7% орбитального периода на круговой орбите)
и время падения до точечной массы на радиальной параболической орбите
- (7,5% орбитального периода на круговой орбите)
Тот факт, что формулы отличаются только постоянным коэффициентом, априори ясен из анализа размерностей . [ нужна ссылка ]
Энергия
[ редактировать ]
Удельная орбитальная энергия ( ) отрицательно, и
Таким образом, теорема вириала [1] : 72 применяется даже без усреднения по времени: [ нужна ссылка ]
- кинетическая энергия системы равна абсолютному значению полной энергии
- потенциальная энергия системы равна удвоенной полной энергии
Скорость убегания с любого расстояния в √ 2 раза превышает скорость на круговой орбите на этом расстоянии: кинетическая энергия в два раза больше, следовательно, полная энергия равна нулю. [ нужна ссылка ]
Дельта-v выйдет на круговую орбиту
[ редактировать ]Для перехода на большую круговую орбиту, например, на геостационарную орбиту , требуется большее значение delta-v, чем для уходящей орбиты , хотя последнее подразумевает уход на произвольное расстояние и наличие большего количества энергии, чем необходимо для орбитальной скорости круговой орбиты. Это еще и вопрос выхода на орбиту. См. также переходную орбиту Гомана .
Орбитальная скорость в общей теории относительности
[ редактировать ]В метрике Шварцшильда орбитальная скорость для круговой орбиты с радиусом определяется следующей формулой:
где – радиус Шварцшильда центрального тела.
Вывод
[ редактировать ]Для удобства вывод будем записывать в единицах, в которых .
Четырехскоростное : тело на круговой орбите определяется выражением
( постоянна на круговой орбите, а координаты можно выбрать так, что ). Точка над переменной обозначает дифференцирование по собственному времени. .
Для массивной частицы компоненты четырехскорости удовлетворяют следующему уравнению:
Используем уравнение геодезических:
Единственным нетривиальным уравнением является уравнение для . Это дает:
Из этого мы получаем:
Подстановка этого в уравнение для массивной частицы дает:
Следовательно:
Предположим, у нас есть наблюдатель в радиусе , не движущихся относительно центрального тела, то есть их четырехскорость пропорциональна вектору . Условие нормировки подразумевает, что оно равно:
Скалярное произведение четырех скоростей наблюдателя и вращающегося тела равно гамма-фактору вращающегося тела относительно наблюдателя, следовательно:
Это дает скорость :
Или в единицах СИ:
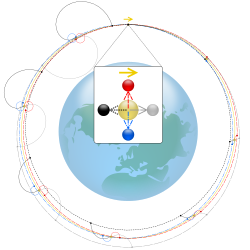
(1 – синий) в сторону Земли,
(2 - красный) вдали от Земли,
(3 - серый) по направлению движения, и
(4 – черный) назад по направлению движения.
Пунктирные эллипсы — это орбиты относительно Земли. Сплошные кривые — возмущения относительно спутника: за один виток (1) и (2) возвращаются к спутнику, совершив виток по часовой стрелке с обеих сторон спутника. Непонятно, что (3) движется все дальше и дальше назад, тогда как (4) движется вперед.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Jump up to: а б с Лиссауэр, Джек Дж.; де Патер, Имке (2019). Фундаментальные планетарные науки: физика, химия и обитаемость . Нью-Йорк, штат Нью-Йорк, США: Издательство Кембриджского университета. п. 604. ИСБН 9781108411981 .







































