Кубооктаэдр
| Кубооктаэдр | |
|---|---|
 | |
| Тип | Архимедово тело |
| Лица | 14 |
| Края | 24 |
| Вершины | 12 |
| Символ Шлефли | |
| Группа симметрии | Октаэдрическая симметрия Тетраэдрическая симметрия |
| Двугранный угол ( градусы ) | примерно 125° |
| Двойной многогранник | Ромбический додекаэдр |
| Характеристики | выпуклый , векторное равновесие, Руперт недвижимость |
| Вершинная фигура | |
 | |
| Сеть | |
 | |
Кубооктаэдр – это многогранник с 8 треугольными гранями и 6 квадратными гранями. Кубооктаэдр имеет 12 одинаковых вершин , в каждой из которых сходятся по 2 треугольника и 2 квадрата, и 24 одинаковых ребра , каждое из которых отделяет треугольник от квадрата. По сути, это квазиправильный многогранник , то есть архимедово тело , которое не только транзитивно по вершинам, но и по ребрам . [1] Он радиально равносторонний . Его двойственный многогранник — ромбдодекаэдр .
Строительство
[ редактировать ]Кубооктаэдр можно построить разными способами:
- Его строительство можно начать со скрепления двух правильных треугольных куполов основанием к основанию. Это похоже на одно из тел Джонсона, треугольный ортобикупол . Разница в том, что треугольный ортобикупол построен с одним из куполов, скрученным так, что подобные многоугольные грани прилегают друг к другу, а кубооктаэдр — нет. В результате кубооктаэдр также можно назвать треугольным гиробикуполом . [2]
- Его построение можно начать с куба или правильного октаэдра , отметив середины их ребер и обрезав в этих точках все вершины. Этот процесс известен как выпрямление , благодаря чему кубооктаэдр получил название выпрямленный куб и выпрямленный октаэдр . [3]
- Альтернативная конструкция — обрезка всех вершин, известная как усечение . можно начать с правильного тетраэдра , обрезав вершины и скосив края. Этот процесс известен как кантелляция , в результате чего кубооктаэдр получил название кантелляционного тетраэдра . [4]
Из всех этих конструкций кубооктаэдр имеет 14 граней: 8 равносторонних треугольников и 6 квадратов. Он также имеет 24 ребра и 12 вершин. [5]
Декартовы координаты вершин кубооктаэдра с длиной ребра с центром в начале координат: [6]
Характеристики
[ редактировать ]Измерение и другие свойства метрик
[ редактировать ]Площадь поверхности кубооктаэдра можно определить суммированием всех площадей его многоугольных граней. Объем кубооктаэдра можно определить, разрезав его на два правильных треугольных купола, просуммировав их объемы. Учитывая, что длина ребра , его площадь поверхности и объем равны: [5]
Двугранный угол кубооктаэдра можно вычислить по углу треугольных куполов. Двугранный угол треугольного купола между квадратом и треугольником составляет примерно 125 °, между квадратом и шестиугольником - 54,7 °, а между треугольником и шестиугольником - 70,5 °. Следовательно, двугранный угол кубооктаэдра между квадратом и треугольником, на ребре, где соединяются основания двух треугольных куполов, равен 54,7° + 70,5°, примерно 125°. Следовательно, двугранный угол кубооктаэдра между квадратом и треугольником составляет примерно 125 °. [7]

Бакминстер Фуллер обнаружил, что кубооктаэдр — единственный многогранник, в котором расстояние между его центром и вершиной такое же, как расстояние между его краями. Другими словами, он имеет векторы одинаковой длины в трехмерном пространстве, известные как вектор равновесия . [8] Жесткие стойки и гибкие вершины кубооктаэдра также могут постепенно трансформироваться в правильный икосаэдр , правильный октаэдр, правильный тетраэдр. Фуллер назвал это преобразованием джиттербага . [9]
Кубооктаэдр обладает свойством Руперта , что означает, что существует многогранник такого же или большего размера, который может пройти через его отверстие. [10]
Симметрия и классификация
[ редактировать ]
Кубооктаэдр — это архимедово тело , то есть это очень симметричный и полуправильный многогранник, в вершине которого встречаются две или более различных правильных многоугольных грани. [11] Кубооктаэдр имеет две симметрии, возникающие в результате упомянутых выше конструкций: ту же симметрию, что и правильный октаэдр или куб, октаэдрическую симметрию. , и та же симметрия, что и правильный тетраэдр, тетраэдрическая симметрия . [12] Многоугольные грани, которые встречаются в каждой вершине, представляют собой два равносторонних треугольника и два квадрата, а фигура вершины кубооктаэдра равна . Двойником кубооктаэдра является ромбдодекаэдр . [13]
Радиальная равносторонняя симметрия
[ редактировать ]В кубооктаэдре длинный радиус (от центра до вершины) равен длине ребра; таким образом, его длинный диаметр (от вершины до противоположной вершины) равен двум длинам ребра. Его центр подобен вершине канонической пирамиды: на расстоянии одного ребра от всех остальных вершин. (В случае кубооктаэдра центр на самом деле является вершиной 6 квадратных и 8 треугольных пирамид). Эта радиальная равносторонняя симметрия является свойством лишь нескольких однородных многогранников , включая двумерный шестиугольник , трехмерный кубооктаэдр и четырехмерный 24- и 8-ячеечный (тессеракт) . Радиально равносторонние многогранники - это те, которые с длинными радиусами могут быть построены из равносторонних треугольников, которые пересекаются в центре многогранника, каждый из которых дает два радиуса и ребро. Следовательно, все внутренние элементы, которые встречаются в центре этих многогранников, имеют внутренние грани равностороннего треугольника, как при разрезе кубооктаэдра на 6 квадратных пирамид и 8 тетраэдров.
Каждый из этих радиально равносторонних многогранников также встречается как ячейки характерной мозаики, заполняющей пространство : мозаика из правильных шестиугольников, выпрямленные кубические соты (чередующиеся кубооктаэдры и октаэдры), соты из 24 ячеек и тессерактические соты соответственно. Каждая тесселяция имеет двойную тесселяцию ; центры ячеек в мозаике являются вершинами ячеек в двойной мозаике. Самая плотная известная регулярная упаковка сфер в двух, трех и четырех измерениях использует центры ячеек одной из этих мозаик в качестве центров сфер.
Поскольку он радиально равносторонний, центр кубооктаэдра находится на расстоянии одной длины ребра от 12 вершин.
Связанные многогранники и соты
[ редактировать ]Кубооктаэдр делит свой скелет с двумя невыпуклыми однородными многогранниками : кубогемиоктаэдром и октагемиоктаэдром . Эти многогранники построены из скелета кубооктаэдра, в котором четыре шестиугольные плоскости делят его диагональ пополам, пересекая его внутреннюю часть. Если сложить шесть квадратов или восемь равносторонних треугольников, то получится кубогемикотаэдр или октагемиоктаэдр соответственно. [14]
Кубооктаэдр 2-покрывает тетраполушестигексаэдр ( два , который соответственно имеет такую же абстрактную вершинную фигуру треугольника и два квадрата: ) и половину вершин, ребер и граней. (Фактическая фигура вершины тетрагемишестиэдра равна , с фактор из-за креста.) [15]
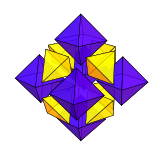
Кубооктаэдр можно разрезать на 6 квадратных пирамид и 8 тетраэдров, сходящихся в центральной точке. Это расчленение выражается в тетраэдрически-октаэдрических сотах , где пары квадратных пирамид объединяются в октаэдры . [16]
График
[ редактировать ]
Скелет кубооктаэдра можно представить в виде графа , одного из графов Архимеда . Он имеет 12 вершин и 24 ребра. Это граф квартики , который состоит из четырех вершин, соединяющих каждую вершину. [17]
Граф кубооктаэдра можно построить как линейный граф куба, в результате чего он становится локально линейным графом . [18]
Появление
[ редактировать ]Кубооктаэдр, вероятно, был известен Платону : цитируют Герона «Определения» Архимеда , который сказал, что Платон знал твердое тело, состоящее из 8 треугольников и 6 квадратов. [19]
Ссылки
[ редактировать ]Сноски
[ редактировать ]- ^ Коксетер 1973 , стр. 18–19, §2.3 Квазиправильные многогранники.
- ^
- ^ ван Леувен, Freixa & Cano 2023 , стр. 50 .
- ^ Линти 2013 , с. 41 .
- ^ Jump up to: а б Берман 1971 .
- ^ Коксетер 1973 , с. 52, §3.7 Координаты вершин правильного и квазиправильного тел.
- ^ Джонсон 1966 .
- ^ Кокрам 2020 , с. 53 .
- ^ Верхейен 1989 .
- ^ Чай, Юань и Замфиреску 2018 .
- ^ Диудея 2018 , с. 39 .
- ^
- Муж и муж (2013) , с. 48
- Кромвель (1997) . Об октаэдрической симметрии см. с. 378 , рисунок 10.13. О тетраэдрической симметрии см . с. 380 , рисунок 10.15.
- ^ Уильямс 1979 , с. 74 .
- ^
- Пизанский и Серватиус 2013 , с. 108
- Барнс 2012 , с. 53
- ^ Грюнбаум 2003 , с. 338 .
- ^ Посаментье и др. 2022 , с. 233–235 .
- ^ Рид и Уилсон 1998 , с. 269.
- ^ Фан 1996 .
- ^ Тернбол 1931 .
Цитируемые работы
[ редактировать ]- Барнс, Дж. (2012). Жемчужины геометрии . Спрингер . дои : 10.1007/978-3-642-30964-9 . ISBN 978-3-642-30964-9 .
- Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329–352. дои : 10.1016/0016-0032(71)90071-8 . МР 0290245 .
- Чай, Ин; Юань, Липин; Замфиреску, Тюдор (2018). «Свойство Руперта архимедовых тел». Американский математический ежемесячник . 125 (6): 497–504. дои : 10.1080/00029890.2018.1449505 . S2CID 125508192 .
- Кокрам, Бернис (2020). В фокусе Сакральная геометрия: ваш личный путеводитель . Уэллфлит Пресс. ISBN 978-1-57715-225-5 .
- Коксетер, HSM (1973) [1948]. Правильные многогранники (3-е изд.). Нью-Йорк: Dover Publications .
- Кромвель, Питер Р. (1997), Многогранники , Издательство Кембриджского университета , ISBN 978-0-521-55432-9
- Дюдя, МВ (2018). Многооболочечные многогранные кластеры . Углеродные материалы: химия и физика. Том. 10. Спрингер . дои : 10.1007/978-3-319-64123-2 . ISBN 978-3-319-64123-2 .
- Фан, Конг (1996). «Об обобщенных клетках». Журнал теории графов . 23 (1): 21–31. doi : 10.1002/(SICI)1097-0118(199609)23:1<21::AID-JGT2>3.0.CO;2-M . МР 1402135 .
- Гика, Матила (1977). Геометрия искусства и жизни ([Начдр.] ред.). Нью-Йорк: Dover Publications . стр. 51–56, 81–84 . ISBN 9780486235424 .
- Грюнбаум, Бранко (2003). « Новые» однородные многогранники». В Бездеке, Андрас (ред.). Дискретная геометрия . ЦРК Пресс . ISBN 9780203911211 .
- Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями» . Канадский математический журнал . 18 : 169–200. дои : 10.4153/cjm-1966-021-8 . МР 0185507 . S2CID 122006114 . Збл 0132.14603 .
- Коджа, М.; Коджа, НЕТ (2013). «Группы Кокстера, кватернионы, симметрии многогранников и 4D-многогранники» . Математическая физика: материалы 13-й региональной конференции, Анталья, Турция, 27–31 октября 2010 г. Всемирная научная.
- Линти, Г. (2013). «Катенированные соединения - Группа 13 [Al, Ga, In, Tl]». В Ридейке, Дж.; Поппельммайер, К. (ред.). Комплексная неорганическая химия II: от элементов к приложениям . Ньюнес.
- Огиевецкий О.; Шлосман, С. (2021). «Платоновые соединения и цилиндры». У Новикова С.; Кричевер И.; Огиевецкий О.; Шлосман, С. (ред.). Интегрируемость, квантование и геометрия. II. Квантовые теории и алгебраическая геометрия . Американское математическое общество . ISBN 978-1-4704-5592-7 .
- Писански, Т.; Серватиус, Б. (2013). Конфигурация с графической точки зрения . Спрингер. дои : 10.1007/978-0-8176-8364-1 . ISBN 978-0-8176-8363-4 .
- Посаментье, А.С.; Таллер, Б.; Дорнер, К.; Геретшлегер, Р.; Мареш, Г.; Шпрейцер, К.; Штулпфаррер, Д. (2022). Геометрия в нашем трехмерном мире . Всемирная научная .
- Читай, RC; Уилсон, Р.Дж. (1998). Атлас графов . Издательство Оксфордского университета .
- Тернбол, HW (1931). «Руководство по греческой математике». Природа . 128 (3235): 739–740. Бибкод : 1931Natur.128..739T . дои : 10.1038/128739a0 . S2CID 3994109 .
- ван Леувен, П.; Фрейша, З.; Кано, И. (2023). «Введение в киральность». Энантиоселективные реакции образования связей CC: с металлокомплексной, органо- и биокаталитической точек зрения . Академическая пресса . ISBN 978-0-443-15774-5 .
- Верхейен, Х.Ф. (1989). «Комплект джиттербаг-трансформаторов и анализ их движения». Компьютеры и математика с приложениями . 17 (1–3): 203–250. дои : 10.1016/0898-1221(89)90160-0 . МР 0994201 .
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 978-0-486-23729-9 .
Внешние ссылки
[ редактировать ]- Однородные многогранники
- Многогранники виртуальной реальности Энциклопедия многогранников
- Вайсштейн, Эрик В. , « Кубооктаэдр » (« Архимедово тело ») в MathWorld .
- Кубооктаэдр на Hexnet, веб-сайте, посвященном математике шестиугольников.
- Клитцинг, Ричард. «3D выпуклые однородные многогранники o3x4o - co» .
- Редактируемая сетка кубооктаэдра для печати с интерактивным 3D-просмотром






























