Правильный 4-многогранник

В математике правильный 4-многогранник или правильный многогранник — это правильный четырёхмерный многогранник . Это четырехмерные аналоги правильных многогранников в трех измерениях и правильных многоугольников в двух измерениях.
Всего имеется шесть выпуклых и десять звездчатых правильных четырехмерных многогранников, всего шестнадцать.
История
[ редактировать ]Выпуклые правильные 4-многогранники были впервые описаны швейцарским математиком Людвигом Шлефли в середине 19 века. [1] Он обнаружил, что таких фигур ровно шесть.
Шлефли также нашел четыре правильных звездных 4-многогранника: большой 120-ячеечный , большой звездчатый 120-ячеечный , большой 600-ячеечный и большой большой звездчатый 120-ячеечный . Он пропустил оставшиеся шесть, потому что не допускал форм, не удовлетворяющих эйлеровой характеристике, в ячейках или фигурах вершин (для торов с нулевыми дырками: F - E + V = 2). Это исключает ячейки и вершинные фигуры, такие как большой додекаэдр {5, 5 / 2 } и малый звездчатый додекаэдр { 5 / 2 ,5}.
Эдмунд Гесс (1843–1903) опубликовал полный список в своей немецкой книге 1883 года « Введение в теорию сферического деления» с особым рассмотрением ее применения к теории равноповерхностей и равноугольных многогранников .
Строительство
[ редактировать ]Существование правильного 4-многогранника ограничено существованием правильных многогранников которые образуют его ячейки и на двугранный угол ограничение
чтобы гарантировать, что ячейки встречаются, образуя замкнутую 3-поверхность.
Описанные шесть выпуклых и десять звездчатых многогранников являются единственными решениями этих ограничений.
Существует четыре невыпуклых символа Шлефли {p,q,r}, которые имеют допустимые ячейки {p,q} и фигуры вершин {q,r} и проходят тест на двугранность, но не могут создать конечные фигуры: {3, 5 / 2 ,3}, {4,3, 5 / 2 }, { 5 / 2 ,3,4}, { 5 / 2 ,3, 5 / 2 }.
Правильные выпуклые 4-многогранники
[ редактировать ]Правильные выпуклые 4-многогранники являются четырехмерными аналогами платоновых тел в трех измерениях и выпуклых правильных многоугольников в двух измерениях.
Каждый выпуклый правильный 4-многогранник ограничен набором трехмерных ячеек , которые являются платоновыми телами одного типа и размера. Они соединяются вместе вдоль своих соответствующих граней (лицом к лицу) регулярным образом, образуя поверхность 4 -многогранника, который представляет собой замкнутое искривленное трехмерное пространство (аналогично тому, как поверхность Земли представляет собой замкнутое, искривленное двумерное пространство).
Характеристики
[ редактировать ]Как и их трехмерные аналоги, выпуклые правильные 4-многогранники можно естественным образом упорядочить по размеру как мере четырехмерного содержимого (гиперобъема) для того же радиуса. Каждый больший многогранник в последовательности более округлый , чем его предшественник, и содержит больше содержимого в пределах того же радиуса. [2] У 4-симплексного (5-клеточного) наименьшее содержимое, а у 120-клеточного — самое большое.
| Правильные выпуклые 4-многогранники |
|---|
В следующей таблице перечислены некоторые свойства шести выпуклых правильных 4-многогранников. Все группы симметрии этих 4-многогранников являются группами Кокстера и заданы в обозначениях, описанных в этой статье. Число, следующее за названием группы, является порядком группы.
| Имена | Изображение | Семья | Шлефли Коксетер | V | И | Ф | С | Зеленый. инжир. | Двойной | Группа симметрии | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5-клеточный пентахорон пентатоп 4-симплекс |  | n -симплекс ( Семья ) | {3,3,3} | 5 | 10 | 10 {3} | 5 {3,3} | {3,3} | самодвойственный | A 4 [3,3,3] | 120 |
| 16-ячеечный гексадекашорон 4-ортоплекс |  | n- ортоплекс (Б и семья) | {3,3,4} | 8 | 24 | 32 {3} | 16 {3,3} | {3,4} | 8-ячеечный | Б 4 [4,3,3] | 384 |
| 8-ячеечный октахорон тессеракт 4-кубовый |  | гиперкуб n- куб (Б и семья) | {4,3,3} | 16 | 32 | 24 {4} | 8 {4,3} | {3,3} | 16-ячеечный | ||
| 24-ячеечный икоситетрахорон октаплекс полиоктаэдр (pO) |  | F и семья | {3,4,3} | 24 | 96 | 96 {3} | 24 {3,4} | {4,3} | самодвойственный | FF4 [3,4,3] | 1152 |
| 600-ячеечный гексакосихорон тетраплекс политетраэдр (пТ) |  | n-пятиугольный многогранник ( семья Х ) | {3,3,5} | 120 | 720 | 1200 {3} | 600 {3,3} | {3,5} | 120-ячеечный | Ч 4 [5,3,3] | 14400 |
| 120-ячеечный гекатоникосахорон додекаконтахорон додекаплекс полидодекаэдр (пД) |  | n-пятиугольный многогранник ( семья Х ) | {5,3,3} | 600 | 1200 | 720 {5} | 120 {5,3} | {3,3} | 600-ячеечный | ||
Джон Конвей пропагандировал названия симплекс, ортоплекс, тессеракт, октаплекс или полиоктаэдр (pO), тетраплекс или политетраэдр (pT), а также додекаплекс или полидодекаэдр (pD). [3]
Норман Джонсон защитил названия n-клетка, или пентахорон, гексадекахорон, тессеракт или октахорон, икоситетрахорон, гексакосихорон и гекатоникосахорон (или додекаконтахорон), придумав термин полихорон, являющийся четырехмерной аналогией трехмерного многогранника и двумерного многоугольника, выраженного от греческого корни поли («много») и choros («комната» или «пространство»). [4] [5]
Эйлерова характеристика для всех 4-многогранников равна нулю, мы имеем 4-мерный аналог многогранной формулы Эйлера:
где N k обозначает количество k -граней в многограннике (вершина — 0-грань, ребро — 1-грань и т. д.).
Топология любого данного 4-многогранника определяется его числами Бетти и коэффициентами кручения . [6]
В качестве конфигураций
[ редактировать ]Правильный 4-многогранник можно полностью описать как конфигурационную матрицу, содержащую количество составляющих его элементов. Строки и столбцы соответствуют вершинам, ребрам, граням и ячейкам. Диагональные числа (слева вверху и справа внизу) показывают, сколько элементов каждого элемента встречается во всем 4-многограннике. Недиагональные числа показывают, сколько элементов столбца встречается в элементе строки или рядом с ним. Например, в каждом ребре по 2 вершины (каждое ребро имеет каждой грани сходятся по 2 клетки 2 вершины), а на (каждая грань принадлежит 2 ячейкам) в любом правильном 4-многограннике. Конфигурацию двойного многогранника можно получить, повернув матрицу на 180 градусов. [7] [8]
| 5-клеточный {3,3,3} | 16-ячеечный {3,3,4} | 8-ячеечный {4,3,3} | 24-ячеечный {3,4,3} | 600-ячеечный {3,3,5} | 120-ячеечный {5,3,3} |
|---|---|---|---|---|---|
Визуализация
[ редактировать ]В следующей таблице показаны некоторые двумерные проекции этих 4-многогранников. Различные другие визуализации можно найти по внешним ссылкам ниже. Графики диаграмм Коксетера -Дынкина также приведены под символом Шлефли .
| A 4 = [3,3,3] | Б 4 = [4,3,3] | Ф 4 = [3,4,3] | Ч 4 = [5,3,3] | ||
|---|---|---|---|---|---|
| 5-клеточный | 16-ячеечный | 8-ячеечный | 24-ячеечный | 600-ячеечный | 120-ячеечный |
| {3,3,3} | {3,3,4} | {4,3,3} | {3,4,3} | {3,3,5} | {5,3,3} |
| Твердые 3D ортогональные проекции | |||||
 Тетраэдрический конверт (центрировано по ячейке/вершине) |  Кубический конверт (клеточно-центрированный) |  Кубический конверт (клеточно-центрированный) |  Кубооктаэдрический конверт (клеточно-центрированный) |  Пентакис икосододекаэдрический конверт (вершинно-центрированный) |  Усеченный ромб триаконтаэдр конверт (клеточно-центрированный) |
| Каркасные диаграммы Шлегеля ( Перспективная проекция ) | |||||
 клеточно-центрированный |  клеточно-центрированный |  клеточно-центрированный |  клеточно-центрированный |  Вершинно-центрированный |  клеточно-центрированный |
| Каркасные стереографические проекции ( 3-сферные ) | |||||
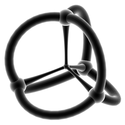 |  | 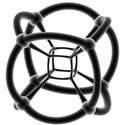 |  |  |  |
Правильная звезда (Шлефли – Гесса) 4-многогранник
[ редактировать ]

представляют 4-многогранники Шлефли – Гесса собой полный набор из 10 правильных самопересекающихся звездчатых полихор ( четырехмерных многогранников ). [10] Они названы в честь своих первооткрывателей: Людвига Шлефли и Эдмунда Гесса . Каждый представлен символом Шлефли { p , q , r }, в котором одно из чисел равно 5/2 . Таким образом, они аналогичны правильным невыпуклым многогранникам Кеплера – Пуансо , которые, в свою очередь, аналогичны пентаграмме.
Имена
[ редактировать ]Их имена, приведенные здесь, были даны Джоном Конвеем , расширяя имена Кэли для многогранников Кеплера-Пуансо : наряду со звездчатыми и великими он добавляет модификатор grand . Конвей предложил следующие рабочие определения:
- звездчатость – заменяет края более длинными краями в тех же линиях. (Пример: пятиугольник превращается в пентаграмму )
- укрупнение – заменяет грани крупными в тех же плоскостях. (Пример: икосаэдр превращается в большой икосаэдр )
- увеличение – заменяет ячейки на большие в тех же трехмерных пространствах. (Пример: 600-ячейка увеличивается в большую 600-ячейку )
Джон Конвей называет 10 форм из 3-х правильных клеточных 4-многогранников: pT=политетраэдр {3,3,5} (тетраэдр из 600 ячеек ), pI=поликосаэдр {3,5, 5 / 2 } ( икосаэдр, 120 ячеек ) и pD=полидодекаэдр {5,3,3} (додекаэдр, 120 ячеек ), с модификаторами префикса: g , a и s для великого, (ag)гранд , и звездчатый. Последняя звездчатая форма, большой звездчатый полидодекаэдр, содержит их всех как gaspD .
Симметрия
[ редактировать ]Все десять полихор обладают [3,3,5]( H 4 ) гексакосихорной симметрией . Они порождаются из 6 связанных тетраэдров Гурса групп симметрии рационального порядка : [3,5,5/2], [5,5/2,5], [5,3,5/2], [5/2,5 ,5/2], [5,5/2,3] и [3,3,5/2].
В каждой группе имеется по 2 правильные звезды-полихоры, за исключением двух самодвойственных групп, имеющих только одну. Итак, среди десяти правильных звездчатых полихор имеются 4 дуальные пары и 2 самодвойственные формы.
Характеристики
[ редактировать ]Примечание:
- Существует 2 уникальных расположения вершин , соответствующих 120-ячеечному и 600-ячеечному .
- Существует 4 уникальных расположения ребер , которые показаны в виде каркасных ортогональных проекций .
- Существует семь уникальных вариантов расположения граней , показанных в виде сплошных (цветных) ортогональных проекций.
Ячейки (многогранники), их грани (многоугольники), многоугольников фигуры ребер и многогранников фигуры вершин идентифицируются их символами Шлефли .
| Имя Конвей (сокр.) | Ортогональный проекция | Шлефли Коксетер | С {п, д} | Ф {р} | И {р} | V {q, р} | Его. | час |
|---|---|---|---|---|---|---|---|---|
| Икосаэдрический 120-ячеечный полиикосаэдр (pI) |  | {3,5,5/2} | 120 {3,5} | 1200 {3} | 720 {5/2 } | 120 {5,5/2} | 4 | 480 |
| Маленький звездчатый, 120 ячеек. звездчатый полидодекаэдр (spD) |  | {5/2,5,3} | 120 {5/2,5} | 720 {5/2} | 1200 {3} | 120 {5,3} | 4 | −480 |
| Отличный 120-ячеечный большой полидодекаэдр (gpD) |  | {5,5/2,5} | 120 {5,5/2} | 720 {5} | 720 {5} | 120 {5/2,5} | 6 | 0 |
| Гранд, 120 ячеек большой полидодекаэдр (apD) |  | {5,3,5/2} | 120 {5,3} | 720 {5} | 720 {5/2} | 120 {3,5/2} | 20 | 0 |
| Большой звездчатый 120-ячеечный большой звездчатый полидодекаэдр (gspD) |  | {5/2,3,5} | 120 {5/2,3} | 720 {5/2} | 720 {5} | 120 {3,5} | 20 | 0 |
| Большой звездчатый, 120 ячеек большой звездчатый полидодекаэдр (aspD) |  | {5/2,5,5/2} | 120 {5/2,5} | 720 {5/2} | 720 {5/2} | 120 {5,5/2} | 66 | 0 |
| Большой гранд, 120 ячеек большой большой полидодекаэдр (gapD) |  | {5,5/2,3} | 120 {5,5/2} | 720 {5} | 1200 {3} | 120 {5/2,3} | 76 | −480 |
| Большой икосаэдр, 120 ячеек. большой полиикосаэдр (gpI) |  | {3,5/2,5} | 120 {3,5/2} | 1200 {3} | 720 {5} | 120 {5/2,5} | 76 | 480 |
| Гранд 600-ячеечный большой политетраэдр (apT) |  | {3,3,5/2} | 600 {3,3} | 1200 {3} | 720 {5/2} | 120 {3,5/2} | 191 | 0 |
| Большой гранд звездчатый, 120 ячеек. большой звездчатый полидодекаэдр (gaspD) |  | {5/2,3,3} | 120 {5/2,3} | 720 {5/2} | 1200 {3} | 600 {3,3} | 191 | 0 |
См. также
[ редактировать ]- Правильный многогранник
- Список правильных многогранников
- Бесконечные правильные 4-многогранники:
- Одна обычная евклидова сота: {4,3,4}
- Четыре компактные правильные гиперболические соты: {3,5,3}, {4,3,5}, {5,3,4}, {5,3,5}
- Одиннадцать паракомпактных правильных гиперболических сот: {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3 ,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5} и {6,3,6}.
- Абстрактные правильные 4-многогранники:
- 11-ячеечный {3,5,3}
- 57-ячеечный {5,3,5}
- Равномерные 4-многогранники, равномерные 4-многогранники, построенные из этих 6 правильных форм.
- Платоново твердое тело
- Многогранники Кеплера-Пуансо — правильный звездчатый многогранник.
- Звездчатый многоугольник — правильные звездчатые многоугольники.
- 4-многогранник
- 5-многогранник
- 6-многогранник
Примечания
[ редактировать ]Ссылки
[ редактировать ]Цитаты
[ редактировать ]- ^ Коксетер 1973 , с. 141, §7-х. Исторические замечания.
- ^ Coxeter 1973 , стр. 292–293, Таблица I (ii): Шестнадцать правильных многогранников { p,q,r } в четырех измерениях.
- ^ Конвей, Бургель и Гудман-Штраусс 2008 , гл. 26. Еще выше
- ^ «Выпуклые и абстрактные многогранники», Программа и рефераты, Массачусетский технологический институт, 2005 г.
- ^ Джонсон, Норман В. (2018). «§ 11.5 Сферические группы Кокстера» . Геометрии и преобразования . Издательство Кембриджского университета. стр. 246–. ISBN 978-1-107-10340-5 .
- ^ Ричесон, Дэвид С. (2012). «23. Анри Пуанкаре и господство топологии» . Жемчужина Эйлера: формула многогранника и рождение топологии . Издательство Принстонского университета. стр. 256–. ISBN 978-0-691-15457-2 .
- ^ Коксетер 1973 , § 1.8 Конфигурации
- ^ Коксетер, Комплексные правильные многогранники, стр.117
- ^ Конвей, Бургель и Гудман-Штраусс 2008 , стр. 406, рис 26.2
- ^ Коксетер, Звездные многогранники и функция Шлефли f(α,β,γ) с. 122 2. Многогранники Шлефли-Гесса.
Библиография
[ редактировать ]- Коксетер, HSM (1973) [1948]. Правильные многогранники (3-е изд.). Нью-Йорк: Дувр.
- Коксетер, HSM (1969). Введение в геометрию (2-е изд.). Уайли. ISBN 0-471-50458-0 .
- ДМИ Соммервилль (2020) [1930]. «X. Правильные многогранники» . Введение в геометрию n измерений . Курьер Дувр. стр. 159–192. ISBN 978-0-486-84248-6 .
- Конвей, Джон Х .; Бургель, Хайди; Гудман-Штраус, Хаим (2008). «26. Правильные звезды-многогранники». Симметрии вещей . стр. 404–8. ISBN 978-1-56881-220-5 .
- Гесс, Эдмунд (1883). «Введение в теорию сферического деления с особым рассмотрением ее применения к теории равноповерхностей и равноугольных многогранников» .
- Гесс, Эдмунд (1885). «О правильных многогранниках высших видов». Встречи по продвижению компанией всех естественных наук в Марбурге : 31–57.
- Шерк, Ф. Артур; Макмаллен, Питер; Томпсон, Энтони К.; Вайс, Азия Ивич, ред. (1995). Калейдоскопы: Избранные сочинения HSM Coxeter . Уайли. ISBN 978-0-471-01003-6 .
- (Документ 10) Коксетер, HSM (1989). «Звездные многогранники и функция Шлафли f(α,β,γ)» . Элементы математики . 44 (2): 25–36.
- Коксетер, HSM (1991). Правильные комплексные многогранники (2-е изд.). Издательство Кембриджского университета. ISBN 978-0-521-39490-1 .
- Макмаллен, Питер; Шульте, Эгон (2002). «Абстрактные правильные многогранники» (PDF) .
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Регулярный полихорон» . Математический мир .
- Джонатан Бауэрс, 16 правильных 4-многогранников
- Обычные развертки 4D-многогранника
- Каталог изображений многогранников Коллекция стереографических проекций 4-многогранников.
- Каталог однородных многогранников
- Dimensions 2-часовой фильм о четвертом измерении (содержит стереографические проекции всех правильных 4-многогранников)
- Правильные многогранники
- Обычная звездная полихора
- Гипертела









































