Расширенная категория
Эта статья нуждается в дополнительных цитатах для проверки . ( август 2019 г. ) |
В теории категорий , разделе математики , обогащенная категория обобщает идею категории путем замены hom-множеств объектами из общей моноидальной категории . Это мотивировано наблюдением, что во многих практических приложениях hom-множество часто имеет дополнительную структуру, которую следует учитывать, например, структуру векторного пространства морфизмов морфизмов или топологического пространства . В обогащенной категории набор морфизмов (гом-множество), связанный с каждой парой объектов, заменяется объектом из некоторой фиксированной моноидальной категории «гом-объектов». Чтобы эмулировать (ассоциативную) композицию морфизмов в обычной категории, hom-категория должна иметь средства составления hom-объектов ассоциативным образом: то есть должна быть бинарная операция над объектами, дающая нам по крайней мере структура моноидальной категории , хотя в некоторых контекстах операция может также нуждаться в коммутативности и, возможно, также иметь правое сопряжение (т. е. сделать категорию симметричной моноидальной или даже симметричный замкнутый моноид соответственно). [ нужна ссылка ]
Таким образом, расширенная теория категорий охватывает в рамках одной и той же структуры широкий спектр структур, включая
- обычные категории, в которых hom-множество несет в себе дополнительную структуру, выходящую за рамки набора. То есть существуют операции или свойства морфизмов, которые должны соблюдаться при композиции (например, существование 2-клеток между морфизмами и их горизонтальная композиция в 2-категории или операция сложения морфизмов в абелевой категории). )
- подобные категориям сущности, которые сами по себе не имеют понятия индивидуального морфизма, но чьи hom-объекты имеют схожие композиционные аспекты (например, предварительные порядки , где правило композиции обеспечивает транзитивность, или метрические пространства Ловера , где hom-объекты представляют собой числовые расстояния, а правило композиции обеспечивает неравенство треугольника).
В случае, когда категория однородных объектов оказывается категорией множеств с обычным декартовым произведением, определения обогащенной категории, обогащенного функтора и т. д. сводятся к исходным определениям из обычной теории категорий.
Обогащенная категория с hom-объектами из моноидальной категории M называется обогащенной категорией над M , или обогащенной категорией в M , или просто M-категорией . Из-за того, что Мак Лейн предпочитал букву V при обозначении моноидальной категории, расширенные категории также иногда обычно называют V-категориями .
Определение [ править ]
Пусть ( M , ⊗, I , α , λ , ρ ) — моноидальная категория . Тогда обогащенная категория C (альтернативно, в ситуациях, когда выбор моноидальной категории должен быть явным, категория, обогащенная по M или M - категория ), состоит из
- класс ob ( C ) объектов C ,
- объект C ( a , b ) из M для каждой пары объектов a , b в C , используемый для определения стрелки в C как стрелка в М ,
- стрелка id a : I → C ( a , a ) в M, обозначающая идентификатор для каждого объекта a в C , и
- стрелка ° abc : C ( b , c ) ⊗ C ( a , b ) → C ( a , c ) в M, обозначающая композицию для каждой тройки объектов a , b , c в C , используемая для определения композиции и в C как вместе с тремя диаграммами передвижения, обсуждаемыми ниже.
Первая диаграмма выражает ассоциативность композиции:
То есть требование ассоциативности теперь берет на себя ассоциатор моноидальной категории M .
В случае, когда M — категория множеств , а (⊗, I , α , λ , ρ ) — моноидальная структура (×, {•}, ...), заданная декартовым произведением , терминальным одноточечным множеством, и канонические изоморфизмы, которые они вызывают, то каждый C ( a , b ) представляет собой множество, элементы которого можно рассматривать как «индивидуальные морфизмы» C , в то время как °, теперь являющаяся функцией, определяет, как составляются последовательные морфизмы. В этом случае каждый путь, ведущий к C ( a , d ) на первой диаграмме, соответствует одному из двух способов составления трёх последовательных индивидуальных морфизмов a → b → c → d , т.е. элементов из C ( a , b ) , C ( б , в ) и C ( в , d ) . В таком случае коммутативность диаграммы — это просто утверждение, что оба порядка композиции дают один и тот же результат, точно так же, как это требуется для обычных категорий.
Новым здесь является то, что вышеизложенное выражает требование ассоциативности без какой-либо явной ссылки на отдельные морфизмы в обогащенной категории C - опять же, эти диаграммы предназначены для морфизмов в моноидальной категории M , а не в C - таким образом создавая концепцию ассоциативности композиция имеет смысл в общем случае, когда hom-объекты C ( a , b ) абстрактны, а сам C не должен даже иметь никакого понятия индивидуального морфизма.
Представление о том, что обычная категория должна иметь тождественные морфизмы, заменяется второй и третьей диаграммами, которые выражают тождество в терминах левого и правого униторов :
и
Возвращаясь к случаю, когда M — категория множеств с декартовым произведением, морфизмы id a : I → C ( a , a ) становятся функциями из одноточечного множества I и должны затем для любого данного объекта a идентифицировать конкретный элемент каждого множества C ( a , a ) , то, что мы можем тогда назвать «тождественным морфизмом для a в C ». Коммутативность последних двух диаграмм — это утверждение о том, что композиции (определённые функциями °), включающие эти выдающиеся отдельные «тождественные морфизмы в C », ведут себя точно так же, как правила тождества для обычных категорий.
Обратите внимание, что здесь упоминаются несколько различных понятий «идентичности»:
- моноидальный тождественный объект I из M , являющийся тождеством для ⊗ только в теоретико- моноидном смысле, и даже тогда только с точностью до канонического изоморфизма ( λ , ρ ) .
- тождественный морфизм 1 C ( a , b ) : C ( a , b ) → C ( a , b ), который M имеет для каждого из своих объектов в силу того, что он является (по крайней мере) обычной категорией.
- расширенная идентичность категории id a : I → C ( a , a ) для каждого объекта a в C , которая снова является морфизмом M , который, даже в случае, когда , что C считается имеет собственные индивидуальные морфизмы, не обязательно является выявление конкретного.
Примеры расширенных категорий [ править ]
- Обычные категории — это категории, обогащенные ( Set , ×, {•}), категорией множеств с декартовым произведением в качестве моноидальной операции, как отмечалось выше.
- 2-Категории — это категории, обогащенные Cat , категорией малых категорий , с моноидальной структурой, задаваемой декартовым произведением. В этом случае 2-клетки между морфизмами a → b и связывающим их правилом вертикальной композиции соответствуют морфизмам обычной категории C ( a , b ) и ее собственному правилу композиции.
- Локально малые категории — это категории, обогащенные ( SmSet , ×), категорией малых множеств с декартовым произведением в качестве моноидальной операции. (Локально малая категория — это категория, чьи hom-объекты представляют собой небольшие множества.)
- Локально конечные категории , по аналогии, — это категории, обогащенные ( FinSet , ×), категорией конечных множеств с декартовым произведением в качестве моноидальной операции.
- Если C — замкнутая моноидальная категория , то C обогащена сама в себе.
- Предварительно упорядоченные множества — это категории, обогащенные определенной моноидальной категорией 2 , состоящей из двух объектов и одной стрелки нетождественности между ними, которую мы можем записать как FALSE → TRUE , соединение как моноидальную операцию и TRUE как ее моноидальную идентичность. Тогда hom-объекты 2 ( a , b ) просто отрицают или подтверждают определенное бинарное отношение к данной паре объектов ( a , b ); ради более привычных обозначений мы можем записать это соотношение как a ≤ b . Существование композиций и идентичности, необходимых для категории, обогащенной более чем на 2, немедленно переводится соответственно в следующие аксиомы:
- b ≤ c и a ≤ b ⇒ a ≤ c (транзитивность)
- ИСТИНА ⇒ a ≤ a (рефлексивность)
- которые являются не чем иным, как аксиомами того, что ≤ является предварительным порядком. А поскольку все диаграммы в 2 коммутируют, это единственное содержание аксиом обогащенной категории для категорий, обогащенных более чем 2 .
- Уильяма Лоувера Обобщенные метрические пространства , также известные как псевдоквазиметрические пространства , представляют собой категории, обогащенные неотрицательными расширенными действительными числами R. +∞ , где последней задается обычная структура категорий посредством обратного ее обычного порядка (т. е. существует морфизм r → s тогда и только тогда, когда r ≥ s ) и моноидальная структура посредством сложения (+) и нуля (0). Хом-объекты R +∞ ( a , b ) по существу являются расстояниями d( a , b ), а существование композиции и идентичности переводится как
- d( b , c ) + d( a , b ) ≥ d( a , c ) (неравенство треугольника)
- 0 ≥ d( а , а )
- Категории с нулевыми морфизмами — это категории, обогащенные ( Set* , ∧), категорией точечных множеств со смешанным произведением в качестве моноидальной операции; особая точка hom-объекта Hom( A , B ) соответствует нулевому морфизму из A в B .
- Категория Ab абелевых групп и категория R-Mod над модулей коммутативным кольцом , а также категория Vect векторных пространств над данным полем обогащаются над собой, где морфизмы наследуют алгебраическую структуру «поточечно». В более общем смысле, преаддитивные категории — это категории, обогащенные ( Ab , ⊗) тензорным произведением как моноидальной операцией (представление абелевых групп как Z -модулей).
с моноидальными функторами Связь
Если существует моноидальный функтор из моноидальной категории M в моноидальную категорию N , то любую категорию, обогащенную над , можно переинтерпретировать как категорию, обогащенную над N. M Каждая моноидальная категория M имеет моноидальный функтор M ( I , –) для категории множеств, поэтому любая обогащенная категория имеет лежащую в основе обычную категорию. Во многих примерах (например, приведенных выше) этот функтор является точным , поэтому категорию, обогащенную по M, можно описать как обычную категорию с определенной дополнительной структурой или свойствами.
Расширенные функторы [ править ]
Обогащенный функтор — это подходящее обобщение понятия функтора на обогащенные категории. В таком случае обогащенные функторы представляют собой отображения между обогащенными категориями, которые соответствуют расширенной структуре.
Если C и D являются M -категориями (то есть категориями, обогащенными моноидальной категорией M ), M -обогащенный функтор T : C → D является отображением, которое присваивает каждому объекту из C объект из D и для каждой пары объектов a и b в C обеспечивает морфизм в MT ab ( : C ( a , b ) → D ( T и a ), T ( b )) между гомо-объектами C D ( которые являются объектами в M ), удовлетворяющий обогащенные версии аксиом функтора, а именно сохранение идентичности и композиции.
Поскольку hom-объекты не обязательно должны быть множествами в обогащенной категории, нельзя говорить о конкретном морфизме. Больше не существует понятия тождественного морфизма или конкретной композиции двух морфизмов. Вместо этого морфизмы единицы в гомо-объект следует рассматривать как выбор идентичности, а морфизмы из моноидального произведения следует рассматривать как композицию. Обычные функториальные аксиомы заменяются соответствующими коммутативными диаграммами, включающими эти морфизмы.
Подробно, имеется диаграмма
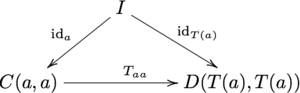
коммутирует, что сводится к уравнению
где I единичный объект M. — Это аналогично правилу F (id a ) = id F ( a ) для обычных функторов. Кроме того, требуется, чтобы диаграмма
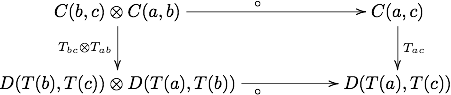
коммутируют, что аналогично правилу F ( fg )= F ( f ) F ( g ) для обычных функторов.
См. также [ править ]
Ссылки [ править ]
- Келли, GM (2005) [1982]. Основные понятия расширенной теории категорий . Переиздания по теории и приложениям категорий. Том. 10.
- Мак Лейн, Сондерс (сентябрь 1998 г.). Категории для работающего математика . Тексты для аспирантов по математике . Том. 5 (2-е изд.). Спрингер. ISBN 0-387-98403-8 .
- Ловере, Ф.В. (2002) [1973]. Метрические пространства, обобщенная логика и закрытые категории . Переиздания по теории и приложениям категорий. Том. 1.
- Расширенная категория в n Lab








