Тетрахорда
В теории музыки тетрахорд тремя ( греч . τετράχορδoν ; латынь : тетрахордум ) представляет собой серию из четырех нот, разделенных интервалами . В традиционной теории музыки тетрахорд всегда охватывал интервал идеальной кварты , соотношение частот 4:3 (около 498 центов ), но в современном использовании он означает любой четырехнотный сегмент гаммы или тонального ряда , не обязательно связанный с ним. к определенной системе настройки.
История
[ редактировать ]Название происходит от тетра (от греческого — «четыре чего-то») и аккорда (от греческого chordon — «струна» или «нота»). В древнегреческой теории музыки тетрахорд обозначал сегмент большей и меньшей совершенных систем, ограниченный неподвижными нотами ( греч . ἑστῶτες ); ноты между ними были подвижными ( греч . κινούμενοι ). Это буквально означает четыре струны , первоначально в отношении инструментов, подобных арфе, таких как лира или кифара, с неявным пониманием того, что четыре струны воспроизводят соседние (то есть соединенные) ноты.
Современная теория музыки использует октаву в качестве основной единицы для определения строя, тогда как древние греки использовали тетрахорд. Древнегреческие теоретики признавали, что октава является фундаментальным интервалом, но считали ее построенной из двух тетрахордов и целого тона . [1]
Теория древнегреческой музыки
[ редактировать ]Древнегреческая теория музыки выделяет три рода (единственное число: род ) тетрахордов. Для этих родов характерен самый большой из трех интервалов тетрахорды:
- Диатонический
- Диатонический тетрахорд имеет характерный интервал, который меньше или равен половине общего интервала тетрахорда (или примерно 249 центов ). Этот характерный интервал обычно несколько меньше (примерно 200 центов), становясь целым тоном . Классически диатонический тетрахорд состоит из двух интервалов тона и одного полутона , например A–G–F–E.
- Хроматический
- Хроматический тетрахорд имеет характерный интервал, который превышает примерно половину общего интервала тетрахорда, но не так велик, как четыре пятых интервала (примерно между 249 и 398 центами). Классически характерным интервалом является малая терция (примерно 300 центов), а два меньших интервала равны полутонам, например A–G ♭ –F–E.
- Энгармонический
- Энгармонический тетрахорд имеет характерный интервал, который превышает примерно четыре пятых общего интервала тетрахорда. Классически характерным интервалом является дитон или большая терция . [2] а два меньших интервала представляют собой четверти тона , например A – G.
–Ф 
-И.
Когда сумма двух меньших интервалов меньше оставшегося ( несложного ) интервала, группа из трех нот называется пикнон (от pyknós , что означает «сжатый»). Это относится к хроматическим и энгармоническим тетрахордам, но не к диатоническому (что означает «вытянутый») тетрахорд.
Каков бы ни был строй тетрахорда, его четыре ступени называются в порядке возрастания: гипат , паргипат , лиханос (или гипермезе ) и меза , а для второго тетрахорда в построении системы - парамезе , трите , паранете и нете. . Hypate фиксированы и находятся и mese , paramese и nete на расстоянии совершенной четверти друг от друга, тогда как положение паргипата и lichanos , или трита и паранете , подвижно.
Поскольку три рода просто представляют собой диапазоны возможных интервалов внутри тетрахорда, были указаны различные оттенки ( хроаи ) со специфическими настройками. После указания рода и оттенка тетрахорда их расположение может дать три основных типа гамм, в зависимости от того, какая нота тетрахорда принимается в качестве первой ноты гаммы. Сами тетрахорды остаются независимыми от гамм, которые они производят, и греческие теоретики никогда не называли их в честь этих гамм. [3]
- Дорианская шкала
- Первая нота тетрахорда также является первой нотой гаммы.
- Диатонический: E–D–C–B | А-Г-Ф-Е
- Хроматический: E–D ♭ –C–B | А–Г ♭ –Ф–Е
- Энгармонический: E – D –С –Б │ А–Г –Ф -И
- Фригийский масштаб
- Вторая нота тетрахорда (в порядке убывания) является первой в гамме.
- Диатонический: D–C–B | А–Г–Ф–Е | Д
- Хроматический: D ♭ –C–B | А – Г ♭ –Ф – Е | Д ♭
- Энгармонический: D –С –Б | А – Г –Ф –Е | Д
- Лидийская шкала
- Третья нота тетрахорда (в порядке убывания) — первая в гамме.
- Диатонический: C–B | А–Г–Ф–Е | округ Колумбия – Ц
- Хроматический: C–B | А – Г ♭ –Ф – Е | Д ♭ –С
- Энгармонический: C –Б | А – Г –Ф –Е | Д –С
Во всех случаях крайние ноты тетрахордов E – B и A – E остаются фиксированными, а промежуточные ноты различаются в зависимости от рода.
Пифагорейские настройки
[ редактировать ]Вот традиционные пифагорейские настройки диатонических и хроматических тетрахордов:
| Диатонический | ||||||
|---|---|---|---|---|---|---|
| раздувать | паргипатировать | лиханос | месяц | |||
| 4 / 3 | 81 / 64 | 9 / 8 | 1 / 1 | |||
| │ | 256 / 243 | │ | 9 / 8 | │ | 9 / 8 | │ |
| −498 ¢ | −408 ¢ | −204 ¢ | 0 ¢ | |||
| Хроматический | ||||||
|---|---|---|---|---|---|---|
| раздувать | паргипатировать | лиханос | месяц | |||
| 4 / 3 | 81 / 64 | 32 / 27 | 1 / 1 | |||
| │ | 256 / 243 | │ | 2187 / 2048 | │ | 32 / 27 | │ |
| −498 ¢ | −408 ¢ | −294 ¢ | 0 ¢ | |||
Вот типичный пифагорейский строй энгармонического рода, приписываемый Архитасу :
| Энгармонический | ||||||
|---|---|---|---|---|---|---|
| раздувать | паргипатировать | лиханос | месяц | |||
| 4 / 3 | 9 / 7 | 5 / 4 | 1 / 1 | |||
| │ | 28 / 27 | │ | 36 / 35 | │ | 5 / 4 | │ |
| −498 ¢ | −435 ¢ | −386 ¢ | 0 ¢ | |||
Количество струн на классической лире различалось в разные эпохи и, возможно, в разных местностях – любимыми числами были четыре, семь и десять. Более крупные гаммы строятся из соединенных или дизъюнктных тетрахордов. Соединённые тетрахорды разделяют одну ноту, а дизъюнктивные тетрахорды разделены дизъюнктивным тоном 9/8 (пифагорейская мажорная секунда). Чередование конъюнктивных и дизъюнктных тетрахордов образует повторяющуюся в октавах гамму (как в знакомой нам диатонической гамме , созданной таким образом из рода диатонических), но это было не единственное расположение.
Греки анализировали роды, используя различные термины, в том числе диатонические, энгармонические и хроматические. Гаммы состоят из соединенных или дизъюнктных тетрахордов.
Это частичная таблица сверхчастичных делений Чалмерса по Гофману. [ ВОЗ? ] [4]
Вариации
[ редактировать ]Романтическая эпоха
[ редактировать ]
– ♭ 
– ♭ 
– ♭ 
(б–а–ж–е). Этот тетрахорд состоит из тритона вместо идеальной кварты. Продолжительность: 0 секунд. 
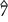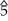– ♭ – ♭ – . Фригийский полукаденс : i – v6 – iv6 – V до минор (басовая линия: c – b ♭ –a ♭ –g) Продолжительность: 0 секунд. Тетрахорды, основанные на настройке равной темперации , использовались для объяснения общих гептатонических гамм . Дан следующий словарь тетрахордов (цифры обозначают количество полутонов в последовательных интервалах тетрахорда в сумме с пятью):
| Тетрахорда | Полушаговая струна |
|---|---|
| Главный | 2 2 1 |
| Незначительный | 2 1 2 |
| Гармонический | 1 3 1 |
| Верхний Минор | 1 2 2 |
следующие гаммы могут быть получены путем соединения двух тетрахордов с целой ступенью (2) между ними: [6] [7]
| Компонентные тетрахорды | Полушаговые стринги | Результирующий масштаб |
|---|---|---|
| Майор + майор | 2 2 1 : 2 : 2 2 1 | Диатонический мажор |
| Минор + верхний минор | 2 1 2 : 2 : 1 2 2 | Натуральный минор |
| Мажор + гармоника | 2 2 1 : 2 : 1 3 1 | Гармонический мажор |
| Минор + гармоника | 2 1 2 : 2 : 1 3 1 | Гармонический минор |
| Гармоника + гармоника | 1 3 1 : 2 : 1 3 1 | Двойная гармоническая шкала [8] [9] или цыганский майор [10] |
| Мажор + верхний минор | 2 2 1 : 2 : 1 2 2 | Мелодичный мажор |
| Минор + мажор | 2 1 2 : 2 : 2 2 1 | Мелодический минор |
| Верхний минор + гармоника | 1 2 2 : 2 : 1 3 1 | Неаполитанский минор |
Все эти гаммы образованы двумя полными дизъюнктными тетрахордами: вопреки греческой и средневековой теории, тетрахорды здесь меняются от гаммы к гамме (т. е. тетрахорд до мажор будет C–D–E–F, ре мажор — D–E –F ♯ –G, до минор C–D–E ♭ –F и т. д.). Теоретики древнегреческой музыки XIX века полагали, что то же самое имело место и в древности, и предполагали, что существовали дорийские, фригийские или лидийские тетрахорды. Это заблуждение было разоблачено в диссертации Отто Гомбози (1939). [11]
Анализ 20-го века
[ редактировать ]Теоретики конца 20-го века часто используют термин «тетрахорд» для описания любого набора из четырех нот при анализе музыки различных стилей и исторических периодов. [12] Выражение «хроматический тетрахорд» может использоваться в двух разных смыслах: для описания особого случая, состоящего из четырехнотного сегмента хроматической гаммы; [13] или, в более исторически ориентированном контексте, для обозначения шести хроматических нот, используемых для заполнения интервала идеальной кварты, обычно встречающегося в нисходящих басовых партиях. [14] Его также можно использовать для описания наборов из менее четырех нот, когда они используются в виде гаммы, чтобы охватить интервал чистой четверти. [15]
Атональное использование
[ редактировать ]Аллен Форте иногда использует термин «тетрахорд» для обозначения того, что он в другом месте называет тетрадой или просто «набором из четырех элементов» - набором из любых четырех высот или классов высот . [16] В теории двенадцати тонов этот термин может иметь особое значение для любых последовательных четырех нот двенадцатитонового ряда. [17]
Незападные весы
[ редактировать ]Тетрахорды, основанные на равнотемперированной настройке, также использовались для приближения к обычным гептатоническим гаммам, используемым в индийской, венгерской, арабской и греческой музыке. Западные теоретики XIX и XX веков, убежденные, что любая гамма должна состоять из двух тетрахордов и тона, описывали различные комбинации, предположительно соответствующие множеству экзотических гамм. Например, следующие диатонические интервалы в один, два или три полутона, всегда в сумме пять полутонов, при соединении целым шагом образуют 36 комбинаций : [18]
| Нижние тетрахорды | Верхние тетрахорды |
|---|---|
| 3 1 1 | 3 1 1 |
| 2 2 1 | 2 2 1 |
| 1 3 1 | 1 3 1 |
| 2 1 2 | 2 1 2 |
| 1 2 2 | 1 2 2 |
| 1 1 3 | 1 1 3 |
Индийская система тетрахордов
[ редактировать ]тетрахорды, разделенные полутоном , Говорят, что также особенно часто встречаются в индийской музыке. В этом случае нижний «тетрахорд» насчитывает шесть полутонов (тритон). Следующие элементы образуют 36 комбинаций при соединении на полшага. [18] Эти 36 комбинаций вместе с 36 описанными выше комбинациями образуют так называемые «72 карнатических лада». [19]
| Нижние тетрахорды | Верхние тетрахорды |
|---|---|
| 3 2 1 | 3 1 1 |
| 3 1 2 | 2 2 1 |
| 2 2 2 | 1 3 1 |
| 1 3 2 | 2 1 2 |
| 2 1 3 | 1 2 2 |
| 1 2 3 | 1 1 3 |
персидский
[ редактировать ]Персидская музыка делит интервал в кварту иначе, чем греческая. Например, Аль-Фараби описывает четыре жанра разделения четвертого: [20]
- Первый жанр, соответствующий греческой диатонике, состоит из тона, тона и полутона, как G–A–B–C.
- Второй жанр состоит из тона, трех четвертных тонов и трех четвертных тонов, как G–A–B. –С.
- Третий жанр имеет тон и четверть, три четверти тона и полутон, как G – A.
–Б–С. - Четвертый жанр, соответствующий греческой хроматике, имеет полутон, полутон и полутон, как G–A ♯ –B–C.
Он продолжает с четырьмя другими возможными жанрами, «разделяя тон на четверти, восьмые, трети, полутрети, четверти трети и комбинируя их различными способами». [21] Позже он представляет возможные положения ладов на лютне, создавая десять интервалов, разделяющих интервал в четверть между струнами: [22]
| Соотношение: | 1 / 1 | 256 / 243 | 18 / 17 | 162 / 149 | 54 / 49 | 9 / 8 | 32 / 27 | 81 / 68 | 27 / 22 | 81 / 64 | 4 / 3 |
| Название заметки: | С | C ♯ | C ♯ | С  | С | Д | E ♭ | E ♭ | И  | И | Ф |
| Центы : | 0 | 90 | 99 | 145 | 168 | 204 | 294 | 303 | 355 | 408 | 498 |
Если учесть, что интервал в кварту между струнами лютни ( уд ) соответствует тетрахорду, а в октаве есть два тетрахорда и мажорный тон , то получится 25-тоновая гамма. Более полное описание деления шкалы (там, где османский, персидский и арабский язык пересекаются) представляет собой 24 четверти тона (см. также арабский макам ). Следует отметить, что аль-Фараби, среди других исламских трактатов, также содержал дополнительные схемы деления, а также давал представление о греческой системе, поскольку часто включались аристоксеновские доктрины. [23]
Композиционные формы
[ редактировать ]Тетрахорд, принципиально незавершенный фрагмент, лежит в основе двух композиционных форм, построенных на повторении этого фрагмента: жалобы и ектении.
Нисходящий тетрахорд от тоники к доминанте, обычно в миноре (например, A–G–F–E в ля миноре), использовался со времен Возрождения для обозначения плача. Хорошо известные случаи включают остинато-бас арии Дидоны « Когда меня положат в землю» в Генри Перселла « Дидоне и Энее» , «Распятие» в Иоганна Себастьяна Баха «Мессе си минор» , BWV 232 или Qui tollis в опере Моцарта . Месса до минор, КВ 427 и др. [24] Этот тетрахорд, известный как lamento («жалоба», «плач»), используется до сих пор. Вариант формы, полный хроматический спуск (например, A–G ♯ –G–F ♯ –F–E ля минор), был известен как Passus duriusculus в Фигуренлере в стиле барокко . [ нужна полная цитата ]
Существует короткая, свободная музыкальная форма эпохи романтизма , называемая жалобой или жалобой (фр.) или плачем . [25] Обычно это набор гармонических вариаций гомофонической текстуры, в которых бас проходит через какой-то тетрахорд, возможно , из предыдущего абзаца, но обычно предполагающий минорный лад . Этот тетрахорд, рассматриваемый как очень короткий основной бас , повторяется снова и снова на протяжении всей композиции.
Другая музыкальная форма того же периода — ектения , или литания (фр.), или литания (др.-анг. шпора). [26] Это также набор гармонических вариаций гомофонической фактуры, но в отличие от плача здесь тетрахордальный фрагмент – восходящий или нисходящий и, возможно, переупорядоченный – установлен в верхнем голосе на манер хоральной прелюдии . Из-за чрезвычайной краткости темы и количества требуемых повторений, а также отсутствия привязки последовательности аккордов к тетрахорду в плаче широта гармонического экскурса в литании обычно заметна.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Матисен, Томас Дж. (2001). «Греция §I: Древняя». В Сэди, С .; Тиррелл, Дж. (ред.). Словарь музыки и музыкантов New Grove (второе изд.). Лондон, Великобритания: Макмиллан. 6 Теория музыки, (iii) Аристоксенианская традиция, (d) Гаммы.
- ^ Чалмерс 1993 , с. 8.
- ^ Чалмерс 1993 , с. 103.
- ^ Чалмерс 1993 , с. 11.
- ^ «Фригийская прогрессия» , Блог классической музыки . Архивировано 6 октября 2011 г. в Wayback Machine.
- ^ Марсель Дюпре, Полный курс органной импровизации , 2 тома, перевод Джона Фенстермейкера. Париж: Альфонс Ледюк, 1962, 2:35. ASIN: B0006CNH8E.
- ^ Джозеф Шиллингер , Система музыкальной композиции Шиллингера , 2 тома. (Нью-Йорк: Карл Фишер, 1941), 1: 112–114. ISBN 978-0306775215 .
- ^ Джошуа Крейг Подольски, Advanced Lead Guitar Concepts (Pacific, Миссури: Мел Бэй, 2010): 111. ISBN 978-0-7866-8236-2 .
- ^ «Двойная гармоническая гамма и ее лады» . docs.solfege.org . Архивировано из оригинала 18 июня 2015 г. Проверено 12 апреля 2015 г.
- ^ Джонатан Беллман , «Стиль hongrois» в музыке Западной Европы (Бостон: Northeastern University Press, 1993): 120. ISBN 1-55553-169-5 .
- ^ Отто Йоханнес Гомбози, Тональность и настроение древней музыки , Копенгаген, Эйнар Мунксгаард, 1939.
- ^ Бенедикт Тейлор, «Модальные сборники из четырех нот в музыке Дворжака американского периода », Music Theory Spectrum 32, вып. 1 (весна 2010 г.): 44–59; Стивен Блок и Джек Даутетт, « Векторные произведения и интервальное взвешивание», Journal of Music Theory 38, вып. 1 (весна 1994 г.): 21–41; Ян Куинн, «Слушая отношения сходства», Перспективы новой музыки 39, вып. 2 (лето 2001 г.): 108–158; Джозеф Н. Штраус, « Построение двенадцати вертикалей Стравинского : аспект гармонии в серийной музыке», Music Theory Spectrum 21, вып. 1 (весна 1999 г.): 43–73; Туире Кууси, «Отношения подмножества-класса, общие высоты звука и общая интервальная структура, определяющая оценку сходства», Music Perception 25, вып. 1 (сентябрь 2007 г.): 1–11; Джошуа Б. Мэйлман , «Воображаемая драма конкурентной оппозиции в « Картера » Скриво в Венто , с примечаниями о повествовании, симметрии, количественном потоке и Гераклите», Музыкальный анализ 28, вып. 2/3 (июль – октябрь 2009 г.): 373–422; Джон Харбисон и Элеонора Кори , « Мартин Бойкан : Струнный квартет (1967): Два взгляда», Перспективы новой музыки 11, вып. 2 (весна – лето 1973 г.): 204–209; Милтон Бэббит , « Эдгар Варез : несколько наблюдений за его музыкой», Перспективы новой музыки 4, вып. 2 (весна – лето 1966 г.): 14–22; Энни К. Йих, «Анализ Дебюсси : тональность, мотивационные наборы и референтная коллекция, специфичная для определенного класса высоты», Music Analysis 19, вып. 2 (июль 2000 г.): 203–229; Дж. К. Рэндалл , « Годфри Уинэма Сочинение для оркестра», Перспективы новой музыки 2, вып. 1 (осень – зима 1963 г.): 102–113.
- ^ Брент Ауэрбах, «Многоуровневая полифония и ее определяющая роль в фортепианной музыке Иоганна Брамса », Журнал теории музыки 52, вып. 2 (осень 2008 г.): 273–320.
- ^ Роберт Голден , «Прерванный тетрахорд Бетховена и Седьмая симфония », Intégral 5 (1991): 77–100.
- ^ Норс С. Джозефсон, «О некоторых очевидных набросках к Восьмой симфонии Сибелиуса », Archives of Musicology 61, № 1 (2004): 54–67.
- ^ Аллен Форте (1973). Структура атональной музыки , стр. 1, 18, 68, 70, 73, 87, 88, 21, 119, 123, 124, 125, 138, 143, 171, 174 и 223. Нью-Хейвен и Лондон: Йельский университет. Нажимать. ISBN 0-300-01610-7 (ткань) ISBN 0-300-02120-8 (пбк). Аллен Форте (1985). «Анализ множества питч-классов сегодня». Музыкальный анализ 4, вып. 1 и 2 (март – июль: специальный выпуск: Королевского колледжа Лондонская конференция по музыкальному анализу , 1984 г.): 29–58, цитаты 48–51, 53.
- ^ Рейнольд Симпсон, «Новые зарисовки, старые фрагменты и Третий струнный квартет Шенберга, соч. 30», Теория и практика 17, В честь Арнольда Шенберга (1) (1992): 85–101.
- ↑ Перейти обратно: Перейти обратно: а б Марсель Дюпре, Полный курс органной импровизации , 2 тома, перевод Джона Фенстермейкера (Париж: Альфонс Ледюк, 1962): 2:35. ASIN: B0006CNH8E.
- ^ Джоанни Гроссет, «Индия. История музыки от зарождения до наших дней», Энциклопедия музыки и словарь консерватории , том. 1, Париж, Делаграв, 1914, с. 325.
- ^ Аль-Фараби 2001 , стр. 56–57.
- ^ Аль-Фараби 2001 , с. 58.
- ^ Аль-Фараби 2001 , стр. 165–179; Либерти Маник, Арабская тональная система в средние века (Лейден, Э. Дж. Брилл, 1969): 42; Хабиб Хасан Тума , Музыка арабов в переводе Лори Шварц. (Портленд, Орегон: Amadeus Press, 1996): 19. ISBN 0-931340-88-8 .
- ^ Чалмерс 1993 , с. 20.
- ^ Эллен Розанд, «Нисходящий тетрахорд: эмблема плача», The Musical Quarterly 65, вып. 3 (1979): 346–59.
- ^ Марсель Дюпре, Полный курс органной импровизации: Подготовленные упражнения , 2 тома, перевод Джона Фенстермейкера. Париж: Альфонс Ледюк, 1937): 1:14.
- ^ Марсель Дюпре, (1962). Полный курс органной импровизации , 2 тома, перевод Джона Фенстермейкера (Париж: Альфонс Ледюк, 1962): 2:110.
Источники
- Аль-Фараби (2001) [1930]. Китабу л-мусики аль-кабир [ арабская музыка ] (переиздание) (на французском языке). Перевод Родольфа д'Эрлангера. Париж: Гетнер.
- Чалмерс, Джон Х. младший (1993). Ларри Полански ; Картер Шольц (ред.). Деления тетрахорда: Пролегомен [введение] в построение музыкальных гамм . предисловие Лу Харрисона . Ганновер, Нью-Гэмпшир: Музыка Фрог Пик. ISBN 0-945996-04-7 .
Дальнейшее чтение
[ редактировать ]- Аноним. 2001. «Тетрахорд». Словарь музыки и музыкантов New Grove , второе издание, под редакцией Стэнли Сэди и Джона Тиррелла . Лондон: Макмиллан.
- Ран, Джон . 1980. Основная атональная теория . Музыкальный сериал Лонгмана. Нью-Йорк и Лондон: Longman Inc.. ISBN 0-582-28117-2 .
- Редер, Джон. 2001. «Сет (ii)». Словарь музыки и музыкантов New Grove , второе издание, под редакцией Стэнли Сэди и Джона Тиррелла . Лондон: Макмиллан.