Зависимость доза-реакция

«Доза-реакция» перенаправляется сюда. Информацию об академическом журнале см. в разделе « Доза – ответ» .

Кривая доза-эффект, показывающая нормализованный ответ ткани на стимуляцию агонистом . Низких доз недостаточно для возникновения ответа, тогда как высокие дозы вызывают максимальный ответ. Самая крутая точка кривой соответствует ЕС _50, равному 0,7 молярного содержания.

Зависимость «доза-реакция» или зависимость «воздействие-реакция описывает величину реакции организма как » функцию воздействия (или доз ) на раздражитель или стрессор (обычно химическое вещество ) после определенного времени воздействия. Зависимость «доза-реакция» можно описать кривыми «доза-реакция» . Это объясняется далее в следующих разделах. Функция реакции на стимул или кривая реакции на стимул определяется в более широком смысле как реакция на любой тип стимула, не ограничиваясь химическими веществами.

Мотивация к изучению зависимости «доза-реакция»

Изучение реакции на дозу и разработка моделей «доза-реакция» имеют центральное значение для определения «безопасных», «опасных» и (где это уместно) полезных уровней и дозировок лекарств, загрязняющих веществ, пищевых продуктов и других веществ, воздействию которых подвергаются люди или другие организмы . Эти выводы часто являются основой государственной политики. Агентство по охране окружающей среды США разработало обширные руководства и отчеты по моделированию и оценке зависимости «доза-реакция», а также программное обеспечение. Управление по санитарному надзору за качеством пищевых продуктов и медикаментов США также имеет рекомендации по разъяснению зависимости «доза-реакция». во время разработки лекарств . Зависимости «доза-эффект» можно использовать у отдельных лиц или в популяциях. Пословица «Доза делает яд» отражает то, что небольшое количество токсина не оказывает существенного эффекта, тогда как большое количество может быть смертельным. Это отражает то, как можно использовать зависимость «доза-реакция» у отдельных людей. В популяциях взаимосвязь «доза-реакция» может описывать то, как группы людей или организмы страдают от различных уровней воздействия. Зависимости «доза-эффект», моделируемые кривыми «доза-эффект», широко используются в фармакологии и разработке лекарств. В частности, форма кривой «доза-реакция» лекарства (количественно определяемая параметрами EC50, nH и ymax) отражает биологическую активность и силу препарата.

Примеры стимулов и реакций

Некоторые примеры показателей зависимости «доза-реакция» показаны в таблицах ниже. Каждый сенсорный стимул соответствует определенному сенсорному рецептору , например никотиновому ацетилхолиновому рецептору никотина или механорецептору механического давления. Однако раздражители (такие как температура или радиация) могут также влиять на физиологические процессы, выходящие за рамки ощущений (и даже вызывать измеримую реакцию смерти). Реакции могут записываться в виде непрерывных данных (например, сила мышечного сокращения) или дискретных данных (например, количество смертей).

Пример стимула		Цель
препарата / токсина Доза	Агонист (например , никотин , изопреналин )	Биохимические рецепторы , Ферменты , Транспортеры
	Антагонист (например , кетамин , пропранолол )
	Аллостерический модулятор (например, бензодиазепин )
Температура		Температурные рецепторы
Уровни звука		Волосковые клетки
Освещенность/Интенсивность света		Фоторецепторы
Механическое давление		Механорецепторы
Доза патогена (например, ЛПС )		н/д
излучения Интенсивность		н/д

Системный уровень	Пример ответа
Население ( эпидемиология )	Смерть, потеря сознания
Организм /Животное в целом ( Физиология )	Тяжесть поражения, артериальное давление, частота сердечных сокращений, объем движений, внимательность, ЭЭГ данные
Орган / Ткань	Производство АТФ, пролиферация, сокращение мышц, выработка желчи, гибель клеток.
Клетка ( Клеточная биология , Биохимия )	Продукция АТФ, сигналы кальция, морфология, митоз

Анализ и создание кривых «доза-реакция»

Полулогарифмические графики гипотетического ответа на агонист, логарифм концентрации по оси x, в сочетании с различными концентрациями антагониста. Параметры кривых и то, как их изменяет антагонист, дают полезную информацию о фармакологическом профиле агониста. Эта кривая похожа, но отличается от той, которая получается при концентрации рецептора, связанного с лигандом, на оси y.

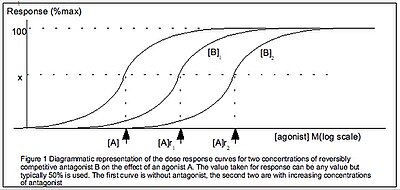
Построение кривых доза-реакция

Кривая доза -реакция представляет собой координатный график, связывающий величину дозы (стимул) с реакцией биологической системы. ряд эффектов (или конечных точек Можно изучить ). Применяемая доза обычно отображается на оси X, а ответ — на оси Y. В некоторых случаях по оси X откладывается логарифм дозы. Кривая обычно имеет сигмоидальную форму , с самой крутой частью посередине. Биологически обоснованные модели, использующие дозу, предпочтительнее использования log(дозы), поскольку последний может визуально подразумевать пороговую дозу, хотя на самом деле ее нет.

Статистический анализ кривых «доза-реакция» может выполняться с помощью регрессионных методов, таких как пробит-модель или логит-модель , или других методов, таких как метод Спирмена-Кербера. Эмпирические модели, основанные на нелинейной регрессии, обычно предпочтительнее использования некоторого преобразования данных, которое линеаризирует зависимость «доза-реакция».

Типичным экспериментальным планом для измерения зависимости «доза-реакция» являются приготовления ванн для органов , анализы связывания лигандов , функциональные анализы и клинические испытания лекарств .

Специально для реагирования на дозы радиации Общество физики здоровья (в США) опубликовало серию документальных фильмов о происхождении линейной беспороговой модели (LNT), хотя общество не приняло политику в отношении LNT».

Уравнение Хилла

Логарифмические кривые «доза-реакция» обычно имеют сигмоидальную форму , монотонны и могут быть адаптированы к классическому уравнению Хилла . Уравнение Хилла представляет собой логистическую функцию по отношению к логарифму дозы и аналогично логит-модели . Также была предложена обобщенная модель для многофазных случаев.

Уравнение Хилла представляет собой следующую формулу, где $E$ это величина ответа, ${\ce {[A]}}$ - концентрация лекарства (или, что то же самое, интенсивность стимула) и $\mathrm {EC} _{50}$ это концентрация препарата, которая вызывает 50% максимальный ответ и $n$ – коэффициент Хилла .

${\frac {E}{E_{\mathrm {max} }}}={\frac {[A]^{n}}{{\text{EC}}_{50}^{n}+[A]^{n}}}={\frac {1}{1+\left({\frac {\mathrm {EC} _{50}}{[A]}}\right)^{n}}}$

Параметры кривой доза-эффект отражают показатели эффективности (например, EC50, IC50, ED50 и т. д.) и меры эффективности (например, тканевую, клеточную или популяционную реакцию).

Обычно используемой кривой доза-реакция является кривая EC ₅₀ , половина максимальной эффективной концентрации, где точка EC ₅₀ определяется как точка перегиба кривой.

Кривые «доза-эффект» обычно соответствуют уравнению Хилла .

Первую точку на графике, где достигается ответ выше нуля (или выше контрольного ответа), обычно называют пороговой дозой. Для большинства полезных или рекреационных наркотиков желаемый эффект достигается в дозах, немного превышающих пороговую дозу. При более высоких дозах появляются нежелательные побочные эффекты , которые усиливаются по мере увеличения дозы. Чем более сильнодействующим является конкретное вещество, тем круче будет эта кривая. В количественных ситуациях ось Y часто обозначается процентами, которые относятся к проценту лиц, подвергшихся воздействию, у которых зарегистрирован стандартный ответ (который может быть смертью, как в LD ₅₀ ). Такая кривая называется квантовой кривой «доза-реакция», в отличие от ступенчатой ​​кривой «доза-реакция», где реакция является непрерывной (либо измеренной, либо оценочной).

Уравнение Хилла можно использовать для описания зависимости «доза-реакция», например, вероятности открытия ионных каналов в зависимости от концентрации лиганда.

Доза обычно измеряется в миллиграммах, микрограммах или граммах на килограмм веса тела при пероральном воздействии или в миллиграммах на кубический метр окружающего воздуха при ингаляционном воздействии. Другие единицы дозы включают моли на массу тела, моли на животное, а при кожном воздействии — моли на квадратный сантиметр.

E _макс. Модель

Модель E _max представляет собой обобщение уравнения Хилла, в котором эффект может быть установлен для нулевой дозы. Используя те же обозначения, что и выше, мы можем выразить модель следующим образом:

$E=E_{0}+{\frac {{[A]}^{n}\times {E_{\mathrm {max} }}}{{[A]}^{n}+\mathrm {EC} _{50}^{n}}}$

Сравните с перестановкой Хилла:

$E_{\mathrm {hill} }={\frac {{[A]}^{n}\times {E_{\mathrm {max} }}}{{[A]}^{n}+\mathrm {EC} _{50}^{n}}}$

Модель E _max является единственной наиболее распространенной моделью для описания зависимости «доза-реакция» при разработке лекарств.

Форма кривой «доза-реакция»

Форма кривой «доза-реакция» обычно зависит от топологии целевой реакционной сети. Хотя форма кривой часто бывает монотонной , в некоторых случаях можно увидеть немонотонные кривые доза-эффект.

Ограничения

Концепция линейной зависимости «доза-реакция», пороговых значений и реакции «все или ничего» может не применяться к нелинейным ситуациям. пороговая модель или линейная беспороговая модель В зависимости от обстоятельств более подходящей может оказаться .Недавняя критика этих моделей применительно к эндокринным разрушителям приводит к необходимости существенного пересмотра моделей тестирования и токсикологии при низких дозах из-за наблюдаемой немонотонности , т.е. U-образных кривых доза/реакция.

Зависимость «доза-реакция» обычно зависит от времени воздействия и пути воздействия (например, при вдыхании, приеме с пищей); количественная оценка реакции после другого времени воздействия или по другому пути приводит к другим взаимосвязям и, возможно, к другим выводам о воздействии рассматриваемого стрессора. Это ограничение вызвано сложностью биологических систем и часто неизвестными биологическими процессами, происходящими между внешним воздействием и неблагоприятной реакцией клеток или тканей.

Анализ щита

Анализ Шильда также может дать представление о влиянии лекарств.

См. также

• Правило Арндта-Шульца
• Потолок эффекта (фармакология)
• Определенный запас прочности
• Гормезис
• Фармакодинамика
• Пространственная эпидемиология
• Закон Вебера-Фехнера
• Фракционирование дозы

Внешние ссылки

• Онлайн-инструмент для анализа ELISA
• Онлайн _{IC 50} калькулятор
• Ecotoxmodels Веб-сайт, посвященный математическим моделям в экотоксикологии , с упором на токсикокинетико-токсикодинамические модели.
• CDD Vault, пример программного обеспечения для подбора кривой «доза-эффект»