Тета-функция

Чтобы узнать о других функциях θ, см. Тета-функция (значения) .

Тета-функция Якоби θ ₁ с номером q = e ^{я п т} = 0,1 е ^{0,1 я р} : ${\begin{aligned}\theta _{1}(z,q)&=2q^{\frac {1}{4}}\sum _{n=0}^{\infty }(-1)^{n}q^{n(n+1)}\sin(2n+1)z\\&=\sum _{n=-\infty }^{\infty }(-1)^{n-{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}e^{(2n+1)iz}.\end{aligned}}$

В математике . тэта-функции представляют собой функции нескольких комплексных переменных специальные Они встречаются во многих темах, включая абелевы многообразия , пространства модулей , квадратичные формы и солитоны . Как алгебры Грассмана , они появляются в квантовой теории поля .

Наиболее распространенной формой тэта-функции является та, которая встречается в теории эллиптических функций . По отношению к одной из комплексных переменных (обычно называемой z ) тэта-функция обладает свойством, выражающим ее поведение относительно сложения периода связанных эллиптических функций, что делает ее квазипериодической функцией . В абстрактной теории эта квазипериодичность происходит из класса когомологий линейного расслоения на комплексном торе , условия спуска .

Одна из интерпретаций тэта-функций при работе с уравнением теплопроводности заключается в том, что «тэта-функция — это специальная функция, которая описывает эволюцию температуры в сегментной области с учетом определенных граничных условий».

На протяжении всей этой статьи $(e^{\pi i\tau })^{\alpha }$ следует интерпретировать как $e^{\alpha \pi i\tau }$ (для решения вопросов выбора филиала ).

Тета-функция Якоби

Существует несколько тесно связанных функций, называемых тета-функциями Якоби, а также множество различных и несовместимых систем обозначений для них. Одна тета-функция Якоби (названная в честь Карла Густава Якоби Якоби ) — это функция, определенная для двух комплексных переменных z и τ , где z может быть любым комплексным числом , а τ — отношение полупериода , ограниченное верхней полуплоскостью , что означает он имеет положительную мнимую часть. Оно определяется формулой

${\begin{aligned}\vartheta (z;\tau )&=\sum _{n=-\infty }^{\infty }\exp \left(\pi in^{2}\tau +2\pi inz\right)\\&=1+2\sum _{n=1}^{\infty }q^{n^{2}}\cos(2\pi nz)\\&=\sum _{n=-\infty }^{\infty }q^{n^{2}}\eta ^{n}\end{aligned}}$

где q = exp( πiτ ) — имя , а η = exp(2 πiz ) . Это форма Якоби . Ограничение гарантирует, что это абсолютно сходящийся ряд. При фиксированном τ это ряд Фурье для 1-периодической целой функции от z . Соответственно, тэта-функция 1-периодична по z :

$\vartheta (z+1;\tau )=\vartheta (z;\tau ).$

Заполняя квадрат , он также становится τ -квазипериодическим по z , причем

$\vartheta (z+\tau ;\tau )=\exp {\bigl (}-\pi i(\tau +2z){\bigr )}\vartheta (z;\tau ).$

Таким образом, в целом

$\vartheta (z+a+b\tau ;\tau )=\exp \left(-\pi ib^{2}\tau -2\pi ibz\right)\vartheta (z;\tau )$

для любых целых чисел a и b .

Для любого фиксированного $\tau$, функция является целой функцией на комплексной плоскости, поэтому по теореме Лиувилля она не может быть двоякопериодической по $1,\tau$ если только оно не является постоянным, и поэтому лучшее, что мы можем сделать, это сделать его периодическим в $1$ и квазипериодический по $\tau$. Действительно, поскольку $$\left|{\frac {\vartheta (z+a+b\tau ;\tau )}{\vartheta (z;\tau )}}\right|=\exp \left(\pi (b^{2}\Im (\tau )+2b\Im (z))\right)$$и $\Im (\tau )>0$, функция $\vartheta (z,\tau )$ неограничено, как того требует теорема Лиувилля.

Фактически это наиболее общая целая функция с двумя квазипериодами в следующем смысле:

Теорема — Если $f:\mathbb {C} \to \mathbb {C}$ является целым и непостоянным и удовлетворяет функциональным уравнениям ${\begin{cases}f(z+1)=f(z)\\f(z+\tau )=e^{az+2\pi ib}f(z)\end{cases}}$для некоторой константы $a,b\in \mathbb {C}$.

Если $a=0$, затем $b=\tau$ и $f(z)=e^{2\pi iz}$. Если $a=-2\pi i$, затем $f(z)=C\vartheta (z+{\frac {1}{2}}\tau +b,\tau )$ для некоторого ненулевого $C\in \mathbb {C}$.

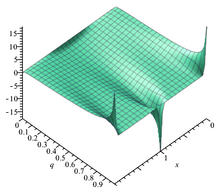
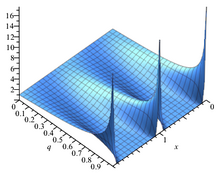
Тета-функция θ ₁ с другим именем q = e ^ipt . Черная точка на правом рисунке показывает, как q меняется с ростом τ .

Тета-функция θ ₁ с другим именем q = e ^ipt . Черная точка на правом рисунке показывает, как q меняется с ростом τ .

Вспомогательные функции

Определенную выше тэта-функцию Якоби иногда рассматривают вместе с тремя вспомогательными тэта-функциями, и в этом случае она записывается с двойным индексом 0:

$\vartheta _{00}(z;\tau )=\vartheta (z;\tau )$

Вспомогательные функции (или полупериодические) определяются формулой

${\begin{aligned}\vartheta _{01}(z;\tau )&=\vartheta \left(z+{\tfrac {1}{2}};\tau \right)\\[3pt]\vartheta _{10}(z;\tau )&=\exp \left({\tfrac {1}{4}}\pi i\tau +\pi iz\right)\vartheta \left(z+{\tfrac {1}{2}}\tau ;\tau \right)\\[3pt]\vartheta _{11}(z;\tau )&=\exp \left({\tfrac {1}{4}}\pi i\tau +\pi i\left(z+{\tfrac {1}{2}}\right)\right)\vartheta \left(z+{\tfrac {1}{2}}\tau +{\tfrac {1}{2}};\tau \right).\end{aligned}}$

Эти обозначения следуют Риману и Мамфорду ; Первоначальная формулировка Якоби использовалась в терминах нома q = e ^ipt а не τ . В обозначениях Якоби θ -функции записываются:

${\begin{aligned}\theta _{1}(z;q)&=\theta _{1}(\pi z,q)=-\vartheta _{11}(z;\tau )\\\theta _{2}(z;q)&=\theta _{2}(\pi z,q)=\vartheta _{10}(z;\tau )\\\theta _{3}(z;q)&=\theta _{3}(\pi z,q)=\vartheta _{00}(z;\tau )\\\theta _{4}(z;q)&=\theta _{4}(\pi z,q)=\vartheta _{01}(z;\tau )\end{aligned}}$

Якоби тета 1

Якоби тета 2

Якоби тета 3

Якоби тета 4

Приведенные выше определения тэта-функций Якоби отнюдь не единственны. См. тета-функции Якоби (варианты обозначений) для дальнейшего обсуждения.

Если мы положим z = 0 в приведенных выше тэта-функциях, мы получим только четыре функции от τ , определенные в верхней полуплоскости. Эти функции называются функциями тета-нульверта , что происходит от немецкого термина, обозначающего нулевое значение , из-за аннулирования левой записи в выражении тета-функции. В качестве альтернативы мы получаем только четыре функции от q , определенные на единичном круге $|q|<1$. Их иногда называют тэта-константами :

${\begin{aligned}\vartheta _{11}(0;\tau )&=-\theta _{1}(q)=-\sum _{n=-\infty }^{\infty }(-1)^{n-1/2}q^{(n+1/2)^{2}}\\\vartheta _{10}(0;\tau )&=\theta _{2}(q)=\sum _{n=-\infty }^{\infty }q^{(n+1/2)^{2}}\\\vartheta _{00}(0;\tau )&=\theta _{3}(q)=\sum _{n=-\infty }^{\infty }q^{n^{2}}\\\vartheta _{01}(0;\tau )&=\theta _{4}(q)=\sum _{n=-\infty }^{\infty }(-1)^{n}q^{n^{2}}\end{aligned}}$

с именем q = e ^ipt . Обратите внимание, что $\theta _{1}(q)=0$. Их можно использовать для определения различных модульных форм и параметризации определенных кривых; в частности, тождество Якоби есть

$\theta _{2}(q)^{4}+\theta _{4}(q)^{4}=\theta _{3}(q)^{4}$

или эквивалентно,

$\vartheta _{01}(0;\tau )^{4}+\vartheta _{10}(0;\tau )^{4}=\vartheta _{00}(0;\tau )^{4}$

что представляет собой кривую Ферма четвертой степени.

Личности Якоби

Тождества Якоби описывают, как тета-функции преобразуются под действием модулярной группы , которая порождается τ ↦ τ + 1 и τ ↦ − ⁠ 1 / τ ⁠ . Уравнения для первого преобразования легко найти, поскольку добавление единицы к τ в показателе степени имеет тот же эффект, что и добавление ⁠ 1 / 2 ⁠ до z ( n ≡ n ² мод 2 ). Для второго пусть

$\alpha =(-i\tau )^{\frac {1}{2}}\exp \left({\frac {\pi }{\tau }}iz^{2}\right).$

Затем

${\begin{aligned}\vartheta _{00}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{00}(z;\tau )\quad &\vartheta _{01}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{10}(z;\tau )\\[3pt]\vartheta _{10}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{01}(z;\tau )\quad &\vartheta _{11}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=-i\alpha \,\vartheta _{11}(z;\tau ).\end{aligned}}$

Тета-функции в терминах нома

Вместо того, чтобы выражать тета-функции через z и τ , мы можем выразить их через аргументы w и ном q , где w = e ^пицца и q = е ^яма . В этом виде функции становятся

${\begin{aligned}\vartheta _{00}(w,q)&=\sum _{n=-\infty }^{\infty }\left(w^{2}\right)^{n}q^{n^{2}}\quad &\vartheta _{01}(w,q)&=\sum _{n=-\infty }^{\infty }(-1)^{n}\left(w^{2}\right)^{n}q^{n^{2}}\\[3pt]\vartheta _{10}(w,q)&=\sum _{n=-\infty }^{\infty }\left(w^{2}\right)^{n+{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}\quad &\vartheta _{11}(w,q)&=i\sum _{n=-\infty }^{\infty }(-1)^{n}\left(w^{2}\right)^{n+{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}.\end{aligned}}$

Мы видим, что тэта-функции также могут быть определены через w и q без прямой ссылки на экспоненциальную функцию. Таким образом, эти формулы можно использовать для определения тета-функций в других полях , где экспоненциальная функция может быть определена не везде, например, в полях p -адических чисел .

Представления продуктов

( Тройное произведение Якоби частный случай тождеств Макдональда ) говорит нам, что для комплексных чисел w и q с | д | < 1 и w ≠ 0, мы имеем

$\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+w^{2}q^{2m-1}\right)\left(1+w^{-2}q^{2m-1}\right)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.$

Это можно доказать элементарными средствами, как, например, в книге Харди и Райта « Введение в теорию чисел» .

Если мы выразим тэта-функцию через ном q = e ^яма (отмечая, что некоторые авторы вместо этого устанавливают q = e ^{2 ямы} ) и возьмем w = e ^пицца затем

$\vartheta (z;\tau )=\sum _{n=-\infty }^{\infty }\exp(\pi i\tau n^{2})\exp(2\pi izn)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.$

Таким образом, мы получаем формулу произведения для тэта-функции в виде

$\vartheta (z;\tau )=\prod _{m=1}^{\infty }{\big (}1-\exp(2m\pi i\tau ){\big )}{\Big (}1+\exp {\big (}(2m-1)\pi i\tau +2\pi iz{\big )}{\Big )}{\Big (}1+\exp {\big (}(2m-1)\pi i\tau -2\pi iz{\big )}{\Big )}.$

С точки зрения w и q :

${\begin{aligned}\vartheta (z;\tau )&=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+q^{2m-1}w^{2}\right)\left(1+{\frac {q^{2m-1}}{w^{2}}}\right)\\&=\left(q^{2};q^{2}\right)_{\infty }\,\left(-w^{2}q;q^{2}\right)_{\infty }\,\left(-{\frac {q}{w^{2}}};q^{2}\right)_{\infty }\\&=\left(q^{2};q^{2}\right)_{\infty }\,\theta \left(-w^{2}q;q^{2}\right)\end{aligned}}$

где ( ; ) _∞ — символ q -Похгаммера , а θ (; ) — q -тэта-функция . Раскрывая члены, тройное произведение Якоби также можно записать

$\prod _{m=1}^{\infty }\left(1-q^{2m}\right){\Big (}1+\left(w^{2}+w^{-2}\right)q^{2m-1}+q^{4m-2}{\Big )},$

который мы также можем записать как

$\vartheta (z\mid q)=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right).$

Эта форма в целом действительна, но, очевидно, представляет особый интерес, когда z действительно. Аналогичные формулы произведения для вспомогательных тэта-функций:

${\begin{aligned}\vartheta _{01}(z\mid q)&=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right),\\[3pt]\vartheta _{10}(z\mid q)&=2q^{\frac {1}{4}}\cos(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m}+q^{4m}\right),\\[3pt]\vartheta _{11}(z\mid q)&=-2q^{\frac {1}{4}}\sin(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m}+q^{4m}\right).\end{aligned}}$

В частности, $$\lim _{q\to 0}{\frac {\vartheta _{10}(z\mid q)}{2q^{\frac {1}{4}}}}=\cos(\pi z),\quad \lim _{q\to 0}{\frac {-\vartheta _{11}(z\mid q)}{2q^{-{\frac {1}{4}}}}}=\sin(\pi z)$$поэтому мы можем интерпретировать их как однопараметрические деформации периодических функций $\sin ,\cos$, что еще раз подтверждает интерпретацию тета-функции как наиболее общей функции 2-квазипериода.

Интегральные представления

Тета-функции Якоби имеют следующие интегральные представления:

${\begin{aligned}\vartheta _{00}(z;\tau )&=-i\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz+\pi u)}{\sin(\pi u)}}\mathrm {d} u;\\[6pt]\vartheta _{01}(z;\tau )&=-i\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz)}{\sin(\pi u)}}\mathrm {d} u;\\[6pt]\vartheta _{10}(z;\tau )&=-ie^{i\pi z+{\frac {1}{4}}i\pi \tau }\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz+\pi u+\pi \tau u)}{\sin(\pi u)}}\mathrm {d} u;\\[6pt]\vartheta _{11}(z;\tau )&=e^{i\pi z+{\frac {1}{4}}i\pi \tau }\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz+\pi \tau u)}{\sin(\pi u)}}\mathrm {d} u.\end{aligned}}$

Функция Тета Нулверта $\theta _{3}(q)$ как это целостное тождество:

$\theta _{3}(q)=1+{\frac {4q{\sqrt {\ln(1/q)}}}{\sqrt {\pi }}}\int _{0}^{\infty }{\frac {\exp[-\ln(1/q)\,x^{2}]\{1-q^{2}\cos[2\ln(1/q)\,x]\}}{1-2q^{2}\cos[2\ln(1/q)\,x]+q^{4}}}\,\mathrm {d} x$

Эта формула обсуждалась в эссе « Преобразования производящей функции квадратного ряда» математика Макси Шмидта из Джорджии в Атланте.

На основе этой формулы приводятся следующие три выдающихся примера:

${\biggl [}{\frac {2}{\pi }}K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}{\biggr ]}^{1/2}=\theta _{3}{\bigl [}\exp(-\pi ){\bigr ]}=1+4\exp(-\pi )\int _{0}^{\infty }{\frac {\exp(-\pi x^{2})[1-\exp(-2\pi )\cos(2\pi x)]}{1-2\exp(-2\pi )\cos(2\pi x)+\exp(-4\pi )}}\,\mathrm {d} x$

${\biggl [}{\frac {2}{\pi }}K({\sqrt {2}}-1){\biggr ]}^{1/2}=\theta _{3}{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}=1+4\,{\sqrt[{4}]{2}}\exp(-{\sqrt {2}}\,\pi )\int _{0}^{\infty }{\frac {\exp(-{\sqrt {2}}\,\pi x^{2})[1-\exp(-2{\sqrt {2}}\,\pi )\cos(2{\sqrt {2}}\,\pi x)]}{1-2\exp(-2{\sqrt {2}}\,\pi )\cos(2{\sqrt {2}}\,\pi x)+\exp(-4{\sqrt {2}}\,\pi )}}\,\mathrm {d} x$

${\biggl \{}{\frac {2}{\pi }}K{\bigl [}\sin {\bigl (}{\frac {\pi }{12}}{\bigr )}{\bigr ]}{\biggr \}}^{1/2}=\theta _{3}{\bigl [}\exp(-{\sqrt {3}}\,\pi ){\bigr ]}=1+4\,{\sqrt[{4}]{3}}\exp(-{\sqrt {3}}\,\pi )\int _{0}^{\infty }{\frac {\exp(-{\sqrt {3}}\,\pi x^{2})[1-\exp(-2{\sqrt {3}}\,\pi )\cos(2{\sqrt {3}}\,\pi x)]}{1-2\exp(-2{\sqrt {3}}\,\pi )\cos(2{\sqrt {3}}\,\pi x)+\exp(-4{\sqrt {3}}\,\pi )}}\,\mathrm {d} x$

Более того, тета-примеры $\theta _{3}({\tfrac {1}{2}})$ и $\theta _{3}({\tfrac {1}{3}})$ должно отображаться:

$\theta _{3}{\bigl (}{\frac {1}{2}}{\bigr )}=1+2\sum _{n=1}^{\infty }{\frac {1}{2^{n^{2}}}}=1+2\pi ^{-1/2}{\sqrt {\ln(2)}}\int _{0}^{\infty }{\frac {\exp[-\ln(2)\,x^{2}]\{16-4\cos[2\ln(2)\,x]\}}{17-8\cos[2\ln(2)\,x]}}\,\mathrm {d} x$

$\theta _{3}{\bigl (}{\frac {1}{2}}{\bigr )}=2.128936827211877158669\ldots$

$\theta _{3}{\bigl (}{\frac {1}{3}}{\bigr )}=1+2\sum _{n=1}^{\infty }{\frac {1}{3^{n^{2}}}}=1+{\frac {4}{3}}\pi ^{-1/2}{\sqrt {\ln(3)}}\int _{0}^{\infty }{\frac {\exp[-\ln(3)\,x^{2}]\{81-9\cos[2\ln(3)\,x]\}}{82-18\cos[2\ln(3)\,x]}}\,\mathrm {d} x$

$\theta _{3}{\bigl (}{\frac {1}{3}}{\bigr )}=1.691459681681715341348\ldots$

Явные значения

Лемнискатические значения

Большая часть этих результатов принадлежит Рамануджану. См. потерянную записную книжку Рамануджана и соответствующую ссылку на функцию Эйлера . Результаты Рамануджана, приведенные в функции Эйлера, плюс несколько элементарных операций дают результаты, приведенные ниже, поэтому они либо находятся в потерянной записной книжке Рамануджана, либо следуют непосредственно из нее. См. также Йи (2004). Определять,

$\quad \varphi (q)=\vartheta _{00}(0;\tau )=\theta _{3}(0;q)=\sum _{n=-\infty }^{\infty }q^{n^{2}}$

с именем $q=e^{\pi i\tau },$ $\tau =n{\sqrt {-1}},$ и эта-функция Дедекинда $\eta (\tau ).$ Тогда для $n=1,2,3,\dots$

${\begin{aligned}\varphi \left(e^{-\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}={\sqrt {2}}\,\eta \left({\sqrt {-1}}\right)\\\varphi \left(e^{-2\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {2+{\sqrt {2}}}}{2}}\\\varphi \left(e^{-3\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {1+{\sqrt {3}}}}{\sqrt[{8}]{108}}}\\\varphi \left(e^{-4\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {2+{\sqrt[{4}]{8}}}{4}}\\\varphi \left(e^{-5\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\sqrt {\frac {2+{\sqrt {5}}}{5}}}\\\varphi \left(e^{-6\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt[{4}]{1}}+{\sqrt[{4}]{3}}+{\sqrt[{4}]{4}}+{\sqrt[{4}]{9}}}}{\sqrt[{8}]{12^{3}}}}\\\varphi \left(e^{-7\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt {13+{\sqrt {7}}}}+{\sqrt {7+3{\sqrt {7}}}}}}{{\sqrt[{8}]{14^{3}}}\cdot {\sqrt[{16}]{7}}}}\\\varphi \left(e^{-8\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {{\sqrt {2+{\sqrt {2}}}}+{\sqrt[{8}]{128}}}{4}}\\\varphi \left(e^{-9\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {1+{\sqrt[{3}]{2+2{\sqrt {3}}}}}{3}}\\\varphi \left(e^{-10\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt[{4}]{64}}+{\sqrt[{4}]{80}}+{\sqrt[{4}]{81}}+{\sqrt[{4}]{100}}}}{\sqrt[{4}]{200}}}\\\varphi \left(e^{-11\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {11+{\sqrt {11}}+(5+3{\sqrt {3}}+{\sqrt {11}}+{\sqrt {33}}){\sqrt[{3}]{-44+33{\sqrt {3}}}}+(-5+3{\sqrt {3}}-{\sqrt {11}}+{\sqrt {33}}){\sqrt[{3}]{44+33{\sqrt {3}}}}}}{\sqrt[{8}]{52180524}}}\\\varphi \left(e^{-12\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt[{4}]{1}}+{\sqrt[{4}]{2}}+{\sqrt[{4}]{3}}+{\sqrt[{4}]{4}}+{\sqrt[{4}]{9}}+{\sqrt[{4}]{18}}+{\sqrt[{4}]{24}}}}{2{\sqrt[{8}]{108}}}}\\\varphi \left(e^{-13\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {13+8{\sqrt {13}}+(11-6{\sqrt {3}}+{\sqrt {13}}){\sqrt[{3}]{143+78{\sqrt {3}}}}+(11+6{\sqrt {3}}+{\sqrt {13}}){\sqrt[{3}]{143-78{\sqrt {3}}}}}}{\sqrt[{4}]{19773}}}\\\varphi \left(e^{-14\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt {13+{\sqrt {7}}}}+{\sqrt {7+3{\sqrt {7}}}}+{\sqrt {10+2{\sqrt {7}}}}+{\sqrt[{8}]{28}}{\sqrt {4+{\sqrt {7}}}}}}{\sqrt[{16}]{28^{7}}}}\\\varphi \left(e^{-15\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {7+3{\sqrt {3}}+{\sqrt {5}}+{\sqrt {15}}+{\sqrt[{4}]{60}}+{\sqrt[{4}]{1500}}}}{{\sqrt[{8}]{12^{3}}}\cdot {\sqrt {5}}}}\\2\varphi \left(e^{-16\pi }\right)&=\varphi \left(e^{-4\pi }\right)+{\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt[{4}]{1+{\sqrt {2}}}}{\sqrt[{16}]{128}}}\\\varphi \left(e^{-17\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {{\sqrt {2}}(1+{\sqrt[{4}]{17}})+{\sqrt[{8}]{17}}{\sqrt {5+{\sqrt {17}}}}}{\sqrt {17+17{\sqrt {17}}}}}\\2\varphi \left(e^{-20\pi }\right)&=\varphi \left(e^{-5\pi }\right)+{\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\sqrt {\frac {3+2{\sqrt[{4}]{5}}}{5{\sqrt {2}}}}}\\6\varphi \left(e^{-36\pi }\right)&=3\varphi \left(e^{-9\pi }\right)+2\varphi \left(e^{-4\pi }\right)-\varphi \left(e^{-\pi }\right)+{\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\sqrt[{3}]{{\sqrt[{4}]{2}}+{\sqrt[{4}]{18}}+{\sqrt[{4}]{216}}}}\end{aligned}}$

Если возвести обратную константу Гельфонда в степень обратной нечетному числу, то соответствующее $\vartheta _{00}$ ценности или $\phi$ значения можно представить упрощенно, используя гиперболический лемнискатический синус :

$\varphi {\bigl [}\exp(-{\tfrac {1}{5}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{5}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{5}}{\sqrt {2}}\,\varpi {\bigr )}$

$\varphi {\bigl [}\exp(-{\tfrac {1}{7}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{7}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{7}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{7}}{\sqrt {2}}\,\varpi {\bigr )}$

$\varphi {\bigl [}\exp(-{\tfrac {1}{9}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {4}{9}}{\sqrt {2}}\,\varpi {\bigr )}$

$\varphi {\bigl [}\exp(-{\tfrac {1}{11}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {4}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {5}{11}}{\sqrt {2}}\,\varpi {\bigr )}$

С письмом $\varpi$ ​​константа лемнискаты представлена .

Обратите внимание, что имеют место следующие модульные тождества:

${\begin{aligned}2\varphi \left(q^{4}\right)&=\varphi (q)+{\sqrt {2\varphi ^{2}\left(q^{2}\right)-\varphi ^{2}(q)}}\\3\varphi \left(q^{9}\right)&=\varphi (q)+{\sqrt[{3}]{9{\frac {\varphi ^{4}\left(q^{3}\right)}{\varphi (q)}}-\varphi ^{3}(q)}}\\{\sqrt {5}}\varphi \left(q^{25}\right)&=\varphi \left(q^{5}\right)\cot \left({\frac {1}{2}}\arctan \left({\frac {2}{\sqrt {5}}}{\frac {\varphi (q)\varphi \left(q^{5}\right)}{\varphi ^{2}(q)-\varphi ^{2}\left(q^{5}\right)}}{\frac {1+s(q)-s^{2}(q)}{s(q)}}\right)\right)\end{aligned}}$

где $s(q)=s\left(e^{\pi i\tau }\right)=-R\left(-e^{-\pi i/(5\tau )}\right)$ представляет собой непрерывную дробь Роджерса-Рамануджана :

${\begin{aligned}s(q)&={\sqrt[{5}]{\tan \left({\frac {1}{2}}\arctan \left({\frac {5}{2}}{\frac {\varphi ^{2}\left(q^{5}\right)}{\varphi ^{2}(q)}}-{\frac {1}{2}}\right)\right)\cot ^{2}\left({\frac {1}{2}}\operatorname {arccot} \left({\frac {5}{2}}{\frac {\varphi ^{2}\left(q^{5}\right)}{\varphi ^{2}(q)}}-{\frac {1}{2}}\right)\right)}}\\&={\cfrac {e^{-\pi i/(25\tau )}}{1-{\cfrac {e^{-\pi i/(5\tau )}}{1+{\cfrac {e^{-2\pi i/(5\tau )}}{1-\ddots }}}}}}\end{aligned}}$

Эквиангармонические значения

Математик Брюс Берндт открыл дополнительные значения тета-функции:

${\begin{array}{lll}\varphi \left(\exp(-{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{13/8}\\\varphi \left(\exp(-2{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{13/8}\cos({\tfrac {1}{24}}\pi )\\\varphi \left(\exp(-3{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{7/8}({\sqrt[{3}]{2}}+1)\\\varphi \left(\exp(-4{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-5/3}3^{13/8}{\Bigl (}1+{\sqrt {\cos({\tfrac {1}{12}}\pi )}}{\Bigr )}\\\varphi \left(\exp(-5{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{5/8}\sin({\tfrac {1}{5}}\pi )({\tfrac {2}{5}}{\sqrt[{3}]{100}}+{\tfrac {2}{5}}{\sqrt[{3}]{10}}+{\tfrac {3}{5}}{\sqrt {5}}+1)\end{array}}$

Дальнейшие значения

Многие значения тета-функции и особенно показанную фи-функцию можно представить через гамма-функцию:

${\begin{array}{lll}\varphi \left(\exp(-{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{7/8}\\\varphi \left(\exp(-2{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{1/8}{\Bigl (}1+{\sqrt {{\sqrt {2}}-1}}{\Bigr )}\\\varphi \left(\exp(-3{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{3/8}3^{-1/2}({\sqrt {3}}+1){\sqrt {\tan({\tfrac {5}{24}}\pi )}}\\\varphi \left(\exp(-4{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{-1/8}{\Bigl (}1+{\sqrt[{4}]{2{\sqrt {2}}-2}}{\Bigr )}\\\varphi \left(\exp(-5{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}{\frac {1}{15}}\,2^{3/8}\times \\&&\times {\biggl [}{\sqrt[{3}]{5}}\,{\sqrt {10+2{\sqrt {5}}}}{\biggl (}{\sqrt[{3}]{5+{\sqrt {2}}+3{\sqrt {3}}}}+{\sqrt[{3}]{5+{\sqrt {2}}-3{\sqrt {3}}}}\,{\biggr )}-{\bigl (}2-{\sqrt {2}}\,{\bigr )}{\sqrt {25-10{\sqrt {5}}}}\,{\biggr ]}\\\varphi \left(\exp(-{\sqrt {6}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {5}{24}}\right){\Gamma \left({\tfrac {5}{12}}\right)}^{-1/2}2^{-13/24}3^{-1/8}{\sqrt {\sin({\tfrac {5}{12}}\pi )}}\\\varphi \left(\exp(-{\tfrac {1}{2}}{\sqrt {6}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {5}{24}}\right){\Gamma \left({\tfrac {5}{12}}\right)}^{-1/2}2^{5/24}3^{-1/8}\sin({\tfrac {5}{24}}\pi )\end{array}}$

Степенные теоремы Нома

Теоремы о прямой мощности

Для преображения нома в тэта-функциях можно использовать эти формулы:

$\theta _{2}(q^{2})={\tfrac {1}{2}}{\sqrt {2[\theta _{3}(q)^{2}-\theta _{4}(q)^{2}]}}$

$\theta _{3}(q^{2})={\tfrac {1}{2}}{\sqrt {2[\theta _{3}(q)^{2}+\theta _{4}(q)^{2}]}}$

$\theta _{4}(q^{2})={\sqrt {\theta _{4}(q)\theta _{3}(q)}}$

Квадраты трех тета-функций с нулевым значением с функцией квадрата в качестве внутренней функции также формируются по образцу пифагорейских троек в соответствии с тождеством Якоби. Более того, эти преобразования действительны:

$\theta _{3}(q^{4})={\tfrac {1}{2}}\theta _{3}(q)+{\tfrac {1}{2}}\theta _{4}(q)$

Эти формулы можно использовать для вычисления тета-значений куба нома:

$27\,\theta _{3}(q^{3})^{8}-18\,\theta _{3}(q^{3})^{4}\theta _{3}(q)^{4}-\,\theta _{3}(q)^{8}=8\,\theta _{3}(q^{3})^{2}\theta _{3}(q)^{2}[2\,\theta _{4}(q)^{4}-\theta _{3}(q)^{4}]$

$27\,\theta _{4}(q^{3})^{8}-18\,\theta _{4}(q^{3})^{4}\theta _{4}(q)^{4}-\,\theta _{4}(q)^{8}=8\,\theta _{4}(q^{3})^{2}\theta _{4}(q)^{2}[2\,\theta _{3}(q)^{4}-\theta _{4}(q)^{4}]$

Для расчета тета-значений пятой степени нома можно использовать следующие формулы:

$[\theta _{3}(q)^{2}-\theta _{3}(q^{5})^{2}][5\,\theta _{3}(q^{5})^{2}-\theta _{3}(q)^{2}]^{5}=256\,\theta _{3}(q^{5})^{2}\theta _{3}(q)^{2}\theta _{4}(q)^{4}[\theta _{3}(q)^{4}-\theta _{4}(q)^{4}]$

$[\theta _{4}(q^{5})^{2}-\theta _{4}(q)^{2}][5\,\theta _{4}(q^{5})^{2}-\theta _{4}(q)^{2}]^{5}=256\,\theta _{4}(q^{5})^{2}\theta _{4}(q)^{2}\theta _{3}(q)^{4}[\theta _{3}(q)^{4}-\theta _{4}(q)^{4}]$

Преобразование в кубическом корне нома

Формулы для значений тэта-функции Нулверта из кубического корня эллиптического нома получаются путем сопоставления двух вещественных решений соответствующих уравнений четвертой степени:

${\biggl [}{\frac {\theta _{3}(q^{1/3})^{2}}{\theta _{3}(q)^{2}}}-{\frac {3\,\theta _{3}(q^{3})^{2}}{\theta _{3}(q)^{2}}}{\biggr ]}^{2}=4-4{\biggl [}{\frac {2\,\theta _{2}(q)^{2}\theta _{4}(q)^{2}}{\theta _{3}(q)^{4}}}{\biggr ]}^{2/3}$

${\biggl [}{\frac {3\,\theta _{4}(q^{3})^{2}}{\theta _{4}(q)^{2}}}-{\frac {\theta _{4}(q^{1/3})^{2}}{\theta _{4}(q)^{2}}}{\biggr ]}^{2}=4+4{\biggl [}{\frac {2\,\theta _{2}(q)^{2}\theta _{3}(q)^{2}}{\theta _{4}(q)^{4}}}{\biggr ]}^{2/3}$

Трансформация в пятом корне нома

Непрерывная дробь Роджерса -Рамануджана может быть определена через тэта-функцию Якоби следующим образом:

$R(q)=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}$

$R(q^{2})=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}\cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}$

$R(q^{2})=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{2/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{1/5}$

Попеременная функция цепной дроби Роджерса-Рамануджана S(q) имеет следующие два тождества:

$S(q)={\frac {R(q^{4})}{R(q^{2})R(q)}}=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{1/5}\cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{2/5}$

Значения тета-функции из пятого корня нома можно представить как рациональную комбинацию непрерывных дробей R и S и значений тета-функции из пятой степени нома и самого нома. Следующие четыре уравнения действительны для всех значений q от 0 до 1:

${\frac {\theta _{3}(q^{1/5})}{\theta _{3}(q^{5})}}-1={\frac {1}{S(q)}}{\bigl [}S(q)^{2}+R(q^{2}){\bigr ]}{\bigl [}1+R(q^{2})S(q){\bigr ]}$

$1-{\frac {\theta _{4}(q^{1/5})}{\theta _{4}(q^{5})}}={\frac {1}{R(q)}}{\bigl [}R(q^{2})+R(q)^{2}{\bigr ]}{\bigl [}1-R(q^{2})R(q){\bigr ]}$

$\theta _{3}(q^{1/5})^{2}-\theta _{3}(q)^{2}={\bigl [}\theta _{3}(q)^{2}-\theta _{3}(q^{5})^{2}{\bigr ]}{\biggl [}1+{\frac {1}{R(q^{2})S(q)}}+R(q^{2})S(q)+{\frac {1}{R(q^{2})^{2}}}+R(q^{2})^{2}+{\frac {1}{S(q)}}-S(q){\biggr ]}$

$\theta _{4}(q)^{2}-\theta _{4}(q^{1/5})^{2}={\bigl [}\theta _{4}(q^{5})^{2}-\theta _{4}(q)^{2}{\bigr ]}{\biggl [}1-{\frac {1}{R(q^{2})R(q)}}-R(q^{2})R(q)+{\frac {1}{R(q^{2})^{2}}}+R(q^{2})^{2}-{\frac {1}{R(q)}}+R(q){\biggr ]}$

Теоремы, зависящие от модуля

В сочетании с эллиптическим модулем можно отобразить следующие формулы:

Вот формулы квадрата эллиптического нома:

$\theta _{4}[q(k)]=\theta _{4}[q(k)^{2}]{\sqrt[{8}]{1-k^{2}}}$

$\theta _{4}[q(k)^{2}]=\theta _{3}[q(k)]{\sqrt[{8}]{1-k^{2}}}$

$\theta _{3}[q(k)^{2}]=\theta _{3}[q(k)]\cos[{\tfrac {1}{2}}\arcsin(k)]$

А это эффективная формула куба нома:

$\theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(t^{3}){\bigr ]}{\bigr \}}^{3}{\biggr \rangle }=\theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(t^{3}){\bigr ]}{\bigr \}}{\biggr \rangle }\,3^{-1/2}{\bigl (}{\sqrt {2{\sqrt {t^{4}-t^{2}+1}}-t^{2}+2}}+{\sqrt {t^{2}+1}}\,{\bigr )}^{1/2}$

Для всех реальных ценностей $t\in \mathbb {R}$ теперь упомянутая формула действительна.

И для этой формулы будут приведены два примера:

Первый пример расчета со значением $t=1$ вставлено:

$\theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(1){\bigr ]}{\bigr \}}^{3}{\biggr \rangle }=\theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(1){\bigr ]}{\bigr \}}{\biggr \rangle }\,3^{-1/2}{\bigl (}{\sqrt {3}}+{\sqrt {2}}\,{\bigr )}^{1/2}$

$\theta _{4}{\bigl [}\exp(-3{\sqrt {2}}\,\pi ){\bigr ]}=\theta _{4}{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}\,3^{-1/2}{\bigl (}{\sqrt {3}}+{\sqrt {2}}\,{\bigr )}^{1/2}$

Второй пример расчета со значением $t=\Phi ^{-2}$ вставлено:

$\theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(\Phi ^{-6}){\bigr ]}{\bigr \}}^{3}{\biggr \rangle }=\theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(\Phi ^{-6}){\bigr ]}{\bigr \}}{\biggr \rangle }\,3^{-1/2}{\bigl (}{\sqrt {2{\sqrt {\Phi ^{-8}-\Phi ^{-4}+1}}-\Phi ^{-4}+2}}+{\sqrt {\Phi ^{-4}+1}}\,{\bigr )}^{1/2}$

$\theta _{4}{\bigl [}\exp(-3{\sqrt {10}}\,\pi ){\bigr ]}=\theta _{4}{\bigl [}\exp(-{\sqrt {10}}\,\pi ){\bigr ]}\,3^{-1/2}{\bigl (}{\sqrt {2{\sqrt {\Phi ^{-8}-\Phi ^{-4}+1}}-\Phi ^{-4}+2}}+{\sqrt {\Phi ^{-4}+1}}\,{\bigr )}^{1/2}$

Константа $\Phi$ представляет собой золотого сечения число $\Phi ={\tfrac {1}{2}}({\sqrt {5}}+1)$ точно.

Некоторые особенности сериала

Суммы с тета-функцией в результате

Бесконечная сумма обратных чисел Фибоначчи с нечетными индексами имеет следующее тождество:

$\sum _{n=1}^{\infty }{\frac {1}{F_{2n-1}}}={\frac {\sqrt {5}}{2}}\,\sum _{n=1}^{\infty }{\frac {2(\Phi ^{-2})^{n-1/2}}{1+(\Phi ^{-2})^{2n-1}}}={\frac {\sqrt {5}}{4}}\sum _{a=-\infty }^{\infty }{\frac {2(\Phi ^{-2})^{a-1/2}}{1+(\Phi ^{-2})^{2a-1}}}=$

$={\frac {\sqrt {5}}{4}}\,\theta _{2}(\Phi ^{-2})^{2}={\frac {\sqrt {5}}{8}}{\bigl [}\theta _{3}(\Phi ^{-1})^{2}-\theta _{4}(\Phi ^{-1})^{2}{\bigr ]}$

Не используя выражение тета-функции, можно сформулировать следующее тождество между двумя суммами:

$\sum _{n=1}^{\infty }{\frac {1}{F_{2n-1}}}={\frac {\sqrt {5}}{4}}\,{\biggl [}\sum _{n=1}^{\infty }2\,\Phi ^{-(2n-1)^{2}/2}{\biggr ]}^{2}$

$\sum _{n=1}^{\infty }{\frac {1}{F_{2n-1}}}=1.82451515740692456814215840626732817332\ldots$

Также в этом случае $\Phi ={\tfrac {1}{2}}({\sqrt {5}}+1)$ это снова число золотого сечения .

Бесконечная сумма обратных квадратов чисел Фибоначчи:

$\sum _{n=1}^{\infty }{\frac {1}{F_{n}^{2}}}={\frac {5}{24}}{\bigl [}2\,\theta _{2}(\Phi ^{-2})^{4}-\theta _{3}(\Phi ^{-2})^{4}+1{\bigr ]}={\frac {5}{24}}{\bigl [}\theta _{3}(\Phi ^{-2})^{4}-2\,\theta _{4}(\Phi ^{-2})^{4}+1{\bigr ]}$

Бесконечная сумма обратных чисел Пелля с нечетными индексами:

$\sum _{n=1}^{\infty }{\frac {1}{P_{2n-1}}}={\frac {1}{\sqrt {2}}}\,\theta _{2}{\bigl [}({\sqrt {2}}-1)^{2}{\bigr ]}^{2}={\frac {1}{2{\sqrt {2}}}}{\bigl [}\theta _{3}({\sqrt {2}}-1)^{2}-\theta _{4}({\sqrt {2}}-1)^{2}{\bigr ]}$

Суммы с тэта-функцией в слагаемом

Следующие две серии тождественности были доказаны Иштваном Мезё :

${\begin{aligned}\theta _{4}^{2}(q)&=iq^{\frac {1}{4}}\sum _{k=-\infty }^{\infty }q^{2k^{2}-k}\theta _{1}\left({\frac {2k-1}{2i}}\ln q,q\right),\\[6pt]\theta _{4}^{2}(q)&=\sum _{k=-\infty }^{\infty }q^{2k^{2}}\theta _{4}\left({\frac {k\ln q}{i}},q\right).\end{aligned}}$

Эти соотношения справедливы для всех 0 < q < 1 . Специализируя значения q , мы имеем следующие суммы без параметров:

${\sqrt {\frac {\pi {\sqrt {e^{\pi }}}}{2}}}\cdot {\frac {1}{\Gamma ^{2}\left({\frac {3}{4}}\right)}}=i\sum _{k=-\infty }^{\infty }e^{\pi \left(k-2k^{2}\right)}\theta _{1}\left({\frac {i\pi }{2}}(2k-1),e^{-\pi }\right)$

${\sqrt {\frac {\pi }{2}}}\cdot {\frac {1}{\Gamma ^{2}\left({\frac {3}{4}}\right)}}=\sum _{k=-\infty }^{\infty }{\frac {\theta _{4}\left(ik\pi ,e^{-\pi }\right)}{e^{2\pi k^{2}}}}$

Нули тета-функций Якоби

Все нули тэта-функций Якоби являются простыми нулями и задаются следующим образом:

${\begin{aligned}\vartheta (z;\tau )=\vartheta _{00}(z;\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {1}{2}}+{\frac {\tau }{2}}\\[3pt]\vartheta _{11}(z;\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau \\[3pt]\vartheta _{10}(z;\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {1}{2}}\\[3pt]\vartheta _{01}(z;\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {\tau }{2}}\end{aligned}}$

где m , n — произвольные целые числа.

Связь с дзета-функцией Римана

Отношение

$\vartheta \left(0;-{\frac {1}{\tau }}\right)=\left(-i\tau \right)^{\frac {1}{2}}\vartheta (0;\tau )$

был использован Риманом для доказательства функционального уравнения для дзета-функции Римана с помощью преобразования Меллина

$\Gamma \left({\frac {s}{2}}\right)\pi ^{-{\frac {s}{2}}}\zeta (s)={\frac {1}{2}}\int _{0}^{\infty }{\bigl (}\vartheta (0;it)-1{\bigr )}t^{\frac {s}{2}}{\frac {\mathrm {d} t}{t}}$

можно показать, что он инвариантен при замене s на 1 − s . Соответствующий интеграл для z ≠ 0 приведен в статье о дзета-функции Гурвица .

Связь с эллиптической функцией Вейерштрасса

Тета-функция использовалась Якоби для построения (в форме, адаптированной для легкого расчета) его эллиптических функций как частных четырех вышеупомянутых тета-функций, и могла быть использована им также для построения эллиптических функций Вейерштрасса , поскольку

$\wp (z;\tau )=-{\big (}\log \vartheta _{11}(z;\tau ){\big )}''+c$

где вторая производная относится к z , а константа c определена так, что разложение Лорана ℘ ( z ) при z = 0 имеет нулевой постоянный член.

Связь с q -гамма-функцией

Четвертая тэта-функция – а значит, и все остальные – тесно связана с Джексона q -гамма-функцией соотношением

$\left(\Gamma _{q^{2}}(x)\Gamma _{q^{2}}(1-x)\right)^{-1}={\frac {q^{2x(1-x)}}{\left(q^{-2};q^{-2}\right)_{\infty }^{3}\left(q^{2}-1\right)}}\theta _{4}\left({\frac {1}{2i}}(1-2x)\log q,{\frac {1}{q}}\right).$

Связь с эта-функцией Дедекинда

Пусть η ( τ ) — эта-функция Дедекинда , а аргумент тета-функции — ном q = e ^яма . Затем,

${\begin{aligned}\theta _{2}(q)=\vartheta _{10}(0;\tau )&={\frac {2\eta ^{2}(2\tau )}{\eta (\tau )}},\\[3pt]\theta _{3}(q)=\vartheta _{00}(0;\tau )&={\frac {\eta ^{5}(\tau )}{\eta ^{2}\left({\frac {1}{2}}\tau \right)\eta ^{2}(2\tau )}}={\frac {\eta ^{2}\left({\frac {1}{2}}(\tau +1)\right)}{\eta (\tau +1)}},\\[3pt]\theta _{4}(q)=\vartheta _{01}(0;\tau )&={\frac {\eta ^{2}\left({\frac {1}{2}}\tau \right)}{\eta (\tau )}},\end{aligned}}$

и,

$\theta _{2}(q)\,\theta _{3}(q)\,\theta _{4}(q)=2\eta ^{3}(\tau ).$

См. также модульные функции Вебера .

Эллиптический модуль

Эллиптический модуль ​

$k(\tau )={\frac {\vartheta _{10}(0;\tau )^{2}}{\vartheta _{00}(0;\tau )^{2}}}$

а дополнительный эллиптический модуль равен

$k'(\tau )={\frac {\vartheta _{01}(0;\tau )^{2}}{\vartheta _{00}(0;\tau )^{2}}}$

Производные тэта-функций

Это два одинаковых определения полного эллиптического интеграла второго рода:

$E(k)=\int _{0}^{\pi /2}{\sqrt {1-k^{2}\sin(\varphi )^{2}}}\partial \varphi$

$E(k)={\frac {\pi }{2}}\sum _{a=0}^{\infty }{\frac {[(2a)!]^{2}}{(1-2a)16^{a}(a!)^{4}}}k^{2a}$

Производные функций Тета Нулверта имеют следующие ряды Маклорена:

$\theta _{2}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{2}(x)={\frac {1}{2}}x^{-3/4}+\sum _{n=1}^{\infty }{\frac {1}{2}}(2n+1)^{2}x^{(2n-1)(2n+3)/4}$

$\theta _{3}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{3}(x)=2+\sum _{n=1}^{\infty }2(n+1)^{2}x^{n(n+2)}$

$\theta _{4}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{4}(x)=-2+\sum _{n=1}^{\infty }2(n+1)^{2}(-1)^{n+1}x^{n(n+2)}$

Производные тэта-функций с нулевым значением следующие:

$\theta _{2}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{2}(x)={\frac {1}{2\pi x}}\theta _{2}(x)\theta _{3}(x)^{2}E{\biggl [}{\frac {\theta _{2}(x)^{2}}{\theta _{3}(x)^{2}}}{\biggr ]}$

$\theta _{3}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{3}(x)=\theta _{3}(x){\bigl [}\theta _{3}(x)^{2}+\theta _{4}(x)^{2}{\bigr ]}{\biggl \{}{\frac {1}{2\pi x}}E{\biggl [}{\frac {\theta _{3}(x)^{2}-\theta _{4}(x)^{2}}{\theta _{3}(x)^{2}+\theta _{4}(x)^{2}}}{\biggr ]}-{\frac {\theta _{4}(x)^{2}}{4\,x}}{\biggr \}}$

$\theta _{4}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{4}(x)=\theta _{4}(x){\bigl [}\theta _{3}(x)^{2}+\theta _{4}(x)^{2}{\bigr ]}{\biggl \{}{\frac {1}{2\pi x}}E{\biggl [}{\frac {\theta _{3}(x)^{2}-\theta _{4}(x)^{2}}{\theta _{3}(x)^{2}+\theta _{4}(x)^{2}}}{\biggr ]}-{\frac {\theta _{3}(x)^{2}}{4\,x}}{\biggr \}}$

Две последние упомянутые формулы действительны для всех действительных чисел действительного интервала определения: $-1<x<1\,\cap \,x\in \mathbb {R}$

И эти две последние названные тета-производные функции связаны друг с другом следующим образом:

$\vartheta _{4}(x){\biggl [}{\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{3}(x){\biggr ]}-\vartheta _{3}(x){\biggl [}{\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{4}(x){\biggr ]}={\frac {1}{4\,x}}\,\theta _{3}(x)\,\theta _{4}(x){\bigl [}\theta _{3}(x)^{4}-\theta _{4}(x)^{4}{\bigr ]}$

Производные частных двух из трех упомянутых здесь тэта-функций всегда имеют рациональное отношение к этим трем функциям:

${\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {\theta _{2}(x)}{\theta _{3}(x)}}={\frac {\theta _{2}(x)\,\theta _{4}(x)^{4}}{4\,x\,\theta _{3}(x)}}$

${\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {\theta _{2}(x)}{\theta _{4}(x)}}={\frac {\theta _{2}(x)\,\theta _{3}(x)^{4}}{4\,x\,\theta _{4}(x)}}$

${\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {\theta _{3}(x)}{\theta _{4}(x)}}={\frac {\theta _{3}(x)^{5}-\theta _{3}(x)\,\theta _{4}(x)^{4}}{4\,x\,\theta _{4}(x)}}$

Для вывода этих формул вывода см. статьи Ном (математика) и Модульная лямбда-функция !

Интегралы от тэта-функций

Для тэта-функций эти интегралы действительны:

$\int _{0}^{1}\theta _{2}(x)\,\mathrm {d} x=\sum _{k=-\infty }^{\infty }{\frac {4}{(2k+1)^{2}+4}}=\pi \tanh(\pi )\approx 3.129881$

$\int _{0}^{1}\theta _{3}(x)\,\mathrm {d} x=\sum _{k=-\infty }^{\infty }{\frac {1}{k^{2}+1}}=\pi \coth(\pi )\approx 3.153348$

$\int _{0}^{1}\theta _{4}(x)\,\mathrm {d} x=\sum _{k=-\infty }^{\infty }{\frac {(-1)^{k}}{k^{2}+1}}=\pi \,\operatorname {csch} (\pi )\approx 0.272029$

Представленные окончательные результаты основаны на общих формулах сумм Коши.

Решение уравнения теплопроводности

Тета-функция Якоби является фундаментальным решением одномерного уравнения теплопроводности с пространственно-периодическими граничными условиями. Принимая z = x вещественным и τ = it с действительным и положительным t , мы можем записать

$\vartheta (x;it)=1+2\sum _{n=1}^{\infty }\exp \left(-\pi n^{2}t\right)\cos(2\pi nx)$

которое решает уравнение теплопроводности

${\frac {\partial }{\partial t}}\vartheta (x;it)={\frac {1}{4\pi }}{\frac {\partial ^{2}}{\partial x^{2}}}\vartheta (x;it).$

Это решение тэта-функции является 1-периодическим по x и при t → 0 приближается к периодической дельта-функции или гребенке Дирака в смысле распределений

$\lim _{t\to 0}\vartheta (x;it)=\sum _{n=-\infty }^{\infty }\delta (x-n)$.

Общие решения пространственно-периодической начальной задачи для уравнения теплопроводности можно получить путем свертки начальных данных при t = 0 с тэта-функцией.

Отношение к группе Гейзенберга

Тета-функция Якоби инвариантна относительно действия дискретной подгруппы группы Гейзенберга . Эта инвариантность представлена ​​в статье о тэта-представлении группы Гейзенберга.

Обобщения

Если F — квадратичная форма от n переменных, то тэта-функция, связанная с F, равна

$\theta _{F}(z)=\sum _{m\in \mathbb {Z} ^{n}}e^{2\pi izF(m)}$

с суммой, простирающейся по решетке целых чисел $\mathbb {Z} ^{n}$. Эта тета-функция представляет собой модульную форму веса. ⁠ n / 2 ⁠ (на подгруппе, определенной соответствующим образом) модулярной группы . В разложении Фурье

${\hat {\theta }}_{F}(z)=\sum _{k=0}^{\infty }R_{F}(k)e^{2\pi ikz},$

числа R _F ( k ) называются числами представления формы.

Тета-серия персонажа Дирихле

Для χ примитивный характер Дирихле по модулю q и ν = ⁠ 1 − χ (−1) / 2 ⁠, то

$\theta _{\chi }(z)={\frac {1}{2}}\sum _{n=-\infty }^{\infty }\chi (n)n^{\nu }e^{2i\pi n^{2}z}$

это вес ⁠ 1 / 2 ⁠ + ν модулярная форма уровня 4 q ² и характер

$\chi (d)\left({\frac {-1}{d}}\right)^{\nu },$

что означает

$\theta _{\chi }\left({\frac {az+b}{cz+d}}\right)=\chi (d)\left({\frac {-1}{d}}\right)^{\nu }\left({\frac {\theta _{1}\left({\frac {az+b}{cz+d}}\right)}{\theta _{1}(z)}}\right)^{1+2\nu }\theta _{\chi }(z)$

в любое время

$a,b,c,d\in \mathbb {Z} ^{4},ad-bc=1,c\equiv 0{\bmod {4}}q^{2}.$

Тета-функция Рамануджана

Дополнительная информация: тета-функция Рамануджана и имитация тета-функции.

Тета-функция Римана

Позволять

$\mathbb {H} _{n}=\left\{F\in M(n,\mathbb {C} )\,{\big |}\,F=F^{\mathsf {T}}\,,\,\operatorname {Im} F>0\right\}$

— множество симметричных квадратных матриц , мнимая часть которых положительно определена . $\mathbb {H} _{n}$ называется верхним полупространством Зигеля и является многомерным аналогом верхней полуплоскости . n -мерным аналогом модулярной группы является симплектическая группа Sp(2 n , $\mathbb {Z}$) ; для n = 1 Sp (2, $\mathbb {Z}$) = SL(2, $\mathbb {Z}$) . n конгруэнтных -мерный аналог подгрупп играет

$\ker {\big \{}\operatorname {Sp} (2n,\mathbb {Z} )\to \operatorname {Sp} (2n,\mathbb {Z} /k\mathbb {Z} ){\big \}}.$

Тогда, учитывая τ ∈ $\mathbb {H} _{n}$тэта -функция Римана определяется как

$\theta (z,\tau )=\sum _{m\in \mathbb {Z} ^{n}}\exp \left(2\pi i\left({\tfrac {1}{2}}m^{\mathsf {T}}\tau m+m^{\mathsf {T}}z\right)\right).$

Здесь z ∈ $\mathbb {C} ^{n}$ — n -мерный комплексный вектор, а верхний индекс T обозначает транспонирование . Тогда тэта-функция Якоби является частным случаем, когда n = 1 и τ ∈ $\mathbb {H}$ где $\mathbb {H}$ — верхняя полуплоскость . Одним из основных применений тэта-функции Римана является то, что она позволяет давать явные формулы для мероморфных функций на компактных римановых поверхностях , а также для других вспомогательных объектов, которые занимают видное место в их теории функций, взяв τ в качестве матрицы периода относительно канонический базис для своей первой группы гомологии .

Тета Римана сходится абсолютно и равномерно на компактных подмножествах $\mathbb {C} ^{n}\times \mathbb {H} _{n}$.

Функциональное уравнение

$\theta (z+a+\tau b,\tau )=\exp \left(2\pi i\left(-b^{\mathsf {T}}z-{\tfrac {1}{2}}b^{\mathsf {T}}\tau b\right)\right)\theta (z,\tau )$

которое справедливо для всех векторов a , b ∈ $\mathbb {Z} ^{n}$, и для всех z ∈ $\mathbb {C} ^{n}$ и τ ∈ $\mathbb {H} _{n}$.

Ряд Пуанкаре

Ряд Пуанкаре обобщает тэта-ряд до автоморфных форм относительно произвольных фуксовых групп .

Вывод тета-значений

Идентичность бета-функции Эйлера

Далее в качестве примеров будут выведены три важных значения тета-функции:

Вот как бета-функция Эйлера определяется в ее сокращенной форме:

$\beta (x)={\frac {\Gamma (x)^{2}}{\Gamma (2x)}}$

В общем случае для всех натуральных чисел $n\in \mathbb {N}$ эта формула бета-функции Эйлера действительна:

${\frac {4^{-1/(n+2)}}{n+2}}\csc {\bigl (}{\frac {\pi }{n+2}}{\bigr )}\beta {\biggl [}{\frac {n}{2(n+2)}}{\biggr ]}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{n+2}+1}}}\,\mathrm {d} x$

Примеры эллиптических интегралов

Ниже приведены некоторые эллиптические интегральные сингулярные значения. являются производными:

Полученная функция имеет следующую лемнискатически эллиптическую первообразную: ${\frac {1}{\sqrt {x^{4}+1}}}={\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {1}{2}}F{\biggl [}2\arctan(x);{\frac {1}{2}}{\sqrt {2}}\,{\biggr ]}$ По стоимости $n=2$ появляется эта личность: ${\frac {1}{4{\sqrt {2}}}}\csc {\bigl (}{\frac {\pi }{4}}{\bigr )}\beta {\bigl (}{\frac {1}{4}}{\bigr )}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{4}+1}}}\,\mathrm {d} x={\biggl \{}{\color {blue}{\frac {1}{2}}F{\biggl [}2\arctan(x);{\frac {1}{2}}{\sqrt {2}}\,{\biggr ]}}{\biggr \}}_{x=0}^{x=\infty }=$ $={\frac {1}{2}}F{\bigl (}\pi ;{\frac {1}{2}}{\sqrt {2}}{\bigr )}=K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}$ Этот результат следует из этой цепочки уравнений: ${\color {ForestGreen}K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}={\frac {1}{4}}\beta {\bigl (}{\frac {1}{4}}{\bigr )}}$

Следующая функция имеет следующую эквиангармоническую эллиптическую первообразную: ${\frac {1}{\sqrt {x^{6}+1}}}={\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {1}{6}}{\sqrt[{4}]{27}}F{\biggl [}2\arctan {\biggl (}{\frac {{\sqrt[{4}]{3}}\,x}{\sqrt {x^{2}+1}}}{\biggr )};{\frac {1}{4}}({\sqrt {6}}+{\sqrt {2}}){\biggr ]}$ По стоимости $n=4$ появляется эта личность: ${\frac {1}{6{\sqrt[{3}]{2}}}}\csc {\bigl (}{\frac {\pi }{6}}{\bigr )}\beta {\bigl (}{\frac {1}{3}}{\bigr )}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{6}+1}}}\,\mathrm {d} x={\biggl \{}{\color {blue}{\frac {1}{6}}{\sqrt[{4}]{27}}F{\biggl [}2\arctan {\biggl (}{\frac {{\sqrt[{4}]{3}}\,x}{\sqrt {x^{2}+1}}}{\biggr )};{\frac {1}{4}}({\sqrt {6}}+{\sqrt {2}}){\biggr ]}}{\biggr \}}_{x=0}^{x=\infty }=$ $={\frac {1}{6}}{\sqrt[{4}]{27}}F{\bigl [}2\arctan({\sqrt[{4}]{3}});{\frac {1}{4}}({\sqrt {6}}+{\sqrt {2}}){\bigr ]}={\frac {2}{9}}{\sqrt[{4}]{27}}K{\bigl [}{\frac {1}{4}}({\sqrt {6}}+{\sqrt {2}}){\bigr ]}={\frac {2}{3}}{\sqrt[{4}]{3}}K{\bigl [}{\frac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}$ Этот результат следует из этой цепочки уравнений: ${\color {ForestGreen}K{\bigl [}{\frac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}={\frac {1}{2{\sqrt[{3}]{2}}{\sqrt[{4}]{3}}}}\beta {\bigl (}{\frac {1}{3}}{\bigr )}}$

А следующая функция имеет следующую эллиптическую первообразную: ${\frac {1}{\sqrt {x^{8}+1}}}=$ $={\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}2\arctan {\biggl [}{\frac {2\cos(\pi /8)\,x}{{\sqrt {x^{4}+{\sqrt {2}}\,x^{2}+1}}-x^{2}+1}}{\biggr ]};2{\sqrt[{4}]{2}}\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}+{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}\arcsin {\biggl [}{\frac {2\cos(\pi /8)\,x}{x^{2}+1}}{\biggr ]};\tan {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}$ По стоимости $n=6$ появляется следующее тождество: ${\frac {1}{8{\sqrt[{4}]{2}}}}\csc {\bigl (}{\frac {\pi }{8}}{\bigr )}\beta {\bigl (}{\frac {3}{8}}{\bigr )}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{8}+1}}}\,\mathrm {d} x=$ $={\biggl \langle }{\color {blue}{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}2\arctan {\biggl [}{\frac {2\cos(\pi /8)\,x}{{\sqrt {x^{4}+{\sqrt {2}}\,x^{2}+1}}-x^{2}+1}}{\biggr ]};2{\sqrt[{4}]{2}}\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}+{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}\arcsin {\biggl [}{\frac {2\cos(\pi /8)\,x}{x^{2}+1}}{\biggr ]};\tan {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}}{\biggr \rangle }_{x=0}^{x=\infty }=$ $={\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\bigl [}\pi ;2{\sqrt[{4}]{2}}\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}{\bigr ]}={\frac {1}{2}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}K({\sqrt {2{\sqrt {2}}-2}}{\bigr )}=2\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}K({\sqrt {2}}-1)$ Этот результат следует из этой цепочки уравнений: ${\color {ForestGreen}K({\sqrt {2}}-1)={\frac {1}{8}}{\sqrt[{4}]{2}}\,({\sqrt {2}}+1)\,\beta {\bigl (}{\frac {3}{8}}{\bigr )}}$

Сочетание целостных тождеств с номом

Функция эллиптического имени имеет следующие важные значения:

$q({\tfrac {1}{2}}{\sqrt {2}})=\exp(-\pi )$

$q[{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}})]=\exp(-{\sqrt {3}}\,\pi )$

$q({\sqrt {2}}-1)=\exp(-{\sqrt {2}}\,\pi )$

Доказательство правильности этих значений номов см. в статье Ном (математика) !

На основе этих интегральных тождеств, а также приведенного выше определения и тождеств тэта-функций в том же разделе этой статьи теперь должны быть определены примерные значения тета-нуля:

$\theta _{3}[q(k)]={\sqrt {2\pi ^{-1}K(k)}}$

$\theta _{3}[\exp(-\pi )]=\theta _{3}[q({\tfrac {1}{2}}{\sqrt {2}})]={\sqrt {2\pi ^{-1}K({\tfrac {1}{2}}{\sqrt {2}})}}=2^{-1/2}\pi ^{-1/2}\beta ({\tfrac {1}{4}})^{1/2}=2^{-1/4}{\sqrt[{4}]{\pi }}\,{\Gamma {\bigl (}{\tfrac {3}{4}}{\bigr )}}^{-1}$

$\theta _{3}[\exp(-{\sqrt {3}}\,\pi )]=\theta _{3}{\bigl \{}q{\bigl [}{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}{\bigr \}}={\sqrt {2\pi ^{-1}K{\bigl [}{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}}}=2^{-1/6}3^{-1/8}\pi ^{-1/2}\beta ({\tfrac {1}{3}})^{1/2}$

$\theta _{3}[\exp(-{\sqrt {2}}\,\pi )]=\theta _{3}[q({\sqrt {2}}-1)]={\sqrt {2\pi ^{-1}K({\sqrt {2}}-1)}}=2^{-1/8}\cos({\tfrac {1}{8}}\pi )\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}$

$\theta _{4}[q(k)]={\sqrt[{4}]{1-k^{2}}}\,{\sqrt {2\pi ^{-1}K(k)}}$

$\theta _{4}[\exp(-{\sqrt {2}}\,\pi )]=\theta _{4}[q({\sqrt {2}}-1)]={\sqrt[{4}]{2{\sqrt {2}}-2}}\,{\sqrt {2\pi ^{-1}K({\sqrt {2}}-1)}}=2^{-1/4}\cos({\tfrac {1}{8}}\pi )^{1/2}\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}$

Последовательности разбиения и произведения Поххаммера

Обычная последовательность номеров разделов

Обычная последовательность разделов $P(n)$ само по себе указывает количество способов, которыми положительное целое число $n$ можно разбить на положительные целые слагаемые. Для чисел $n=1$ к $n=5$, соответствующие номера разделов $P$ со всеми связанными номерными разделами перечислены в следующей таблице:

Примеры значений P(n) и связанных с ними числовых разделов

н	П (п)	платные разделы
0	1	() пустой раздел/ пустая сумма
1	1	(1)
2	2	(1+1), (2)
3	3	(1+1+1), (1+2), (3)
4	5	(1+1+1+1), (1+1+2), (2+2), (1+3), (4)
5	7	(1+1+1+1+1), (1+1+1+2), (1+2+2), (1+1+3), (2+3), (1+4), (5)

Производящую функцию регулярной числовой последовательности разделов можно представить через произведение Поххаммера следующим образом:

$\sum _{k=0}^{\infty }P(k)x^{k}={\frac {1}{(x;x)_{\infty }}}=\theta _{3}(x)^{-1/6}\theta _{4}(x)^{-2/3}{\biggl [}{\frac {\theta _{3}(x)^{4}-\theta _{4}(x)^{4}}{16\,x}}{\biggr ]}^{-1/24}$

Суммирование уже упомянутого произведения Похгаммера описывается теоремой о пятиугольных числах следующим образом:

$(x;x)_{\infty }=1+\sum _{n=1}^{\infty }{\bigl [}-x^{{\text{Fn}}(2n-1)}-x^{{\text{Kr}}(2n-1)}+x^{{\text{Fn}}(2n)}+x^{{\text{Kr}}(2n)}{\bigr ]}$

Следующие основные определения применимы к пятиугольным числам и номерам карточных домиков:

${\text{Fn}}(z)={\tfrac {1}{2}}z(3z-1)$

${\text{Kr}}(z)={\tfrac {1}{2}}z(3z+1)$

В качестве дальнейшего применения получается формула третьей степени произведения Эйлера:

$(x;x)^{3}=\prod _{n=1}^{\infty }(1-x^{n})^{3}=\sum _{m=0}^{\infty }(-1)^{m}(2m+1)x^{m(m+1)/2}$

Строгая последовательность номеров разделов

И строгая последовательность разделов $Q(n)$ указывает количество способов, которыми такое положительное целое число $n$ можно разбить на положительные целые слагаемые так, чтобы каждое слагаемое появлялось не более одного раза. и никакое значение слагаемого не встречается повторно. Точно такая же последовательность также генерируется, если в раздел включены только нечетные слагаемые, но эти нечетные слагаемые могут встречаться более одного раза. Оба представления строгой последовательности номеров разделов сравниваются в следующей таблице:

Примеры значений Q(n) и связанных с ними числовых разделов

н	Q(n)	Числовые разделы без повторяющихся слагаемых	Числовые разделы только с нечетными слагаемыми
0	1	() пустой раздел/ пустая сумма	() пустой раздел/ пустая сумма
1	1	(1)	(1)
2	1	(2)	(1+1)
3	2	(1+2), (3)	(1+1+1), (3)
4	2	(1+3), (4)	(1+1+1+1), (1+3)
5	3	(2+3), (1+4), (5)	(1+1+1+1+1), (1+1+3), (5)
6	4	(1+2+3), (2+4), (1+5), (6)	(1+1+1+1+1+1), (1+1+1+3), (3+3), (1+5)
7	5	(1+2+4), (3+4), (2+5), (1+6), (7)	(1+1+1+1+1+1+1), (1+1+1+1+3), (1+3+3), (1+1+5), (7)
8	6	(1+3+4), (1+2+5), (3+5), (2+6), (1+7), (8)	(1+1+1+1+1+1+1+1), (1+1+1+1+1+3), (1+1+3+3), (1+1+1+ 5), (3+5), (1+7)

Производящую функцию строгой числовой последовательности разделов можно представить с помощью произведения Поххаммера:

$\sum _{k=0}^{\infty }Q(k)x^{k}={\frac {1}{(x;x^{2})_{\infty }}}=\theta _{3}(x)^{1/6}\theta _{4}(x)^{-1/3}{\biggl [}{\frac {\theta _{3}(x)^{4}-\theta _{4}(x)^{4}}{16\,x}}{\biggr ]}^{1/24}$

Последовательность номеров переразбиения

Ряд Маклорена для обратной функции ϑ ₀₁ имеет номера последовательности разбиения в качестве коэффициентов с положительным знаком:

${\frac {1}{\theta _{4}(x)}}=\prod _{n=1}^{\infty }{\frac {1+x^{n}}{1-x^{n}}}=\sum _{k=0}^{\infty }{\overline {P}}(k)x^{k}$

${\frac {1}{\theta _{4}(x)}}=1+2x+4x^{2}+8x^{3}+14x^{4}+24x^{5}+40x^{6}+64x^{7}+100x^{8}+154x^{9}+232x^{10}+\dots$

Если для данного числа $k$, все разделы настроены таким образом, что размер слагаемого никогда не увеличивается, и все те слагаемые, которые не имеют слагаемого того же размера слева от себя, могут быть отмечены для каждого раздела этого типа, тогда это будет результирующее число отмеченных разделов в зависимости от $k$ с помощью функции перераспределения ${\overline {P}}(k)$ .

Первый пример:

${\overline {P}}(4)=14$

Эти 14 возможностей разметки разделов существуют для суммы 4:

(4), ( 4 ), (3+1), ( 3 +1), (3+ 1 ), ( 3 + 1 ), (2+2), ( 2 +2), (2+1+1), ( 2 +1+1), (2+ 1 +1), ( 2 + 1 +1), (1+1+1+1), ( 1 +1+1+1)

Второй пример:

${\overline {P}}(5)=24$

Для суммы 5 существуют 24 возможности разметки разделов:

(5), ( 5 ), (4+1), ( 4 +1), (4+ 1 ), ( 4 + 1 ), (3+2), ( 3 +2), (3+ 2 ), ( 3 + 2 ), (3+1+1), ( 3 +1+1), (3+ 1 +1), ( 3 + 1 +1), (2+2+1), ( 2 +2+1), (2+2+ 1 ), ( 2 +2+ 1 ), (2+1+1+1), ( 2 +1+1+1), (2+ 1 +1+1), ( 2 + 1 +1+1), (1+1+1+1+1), ( 1 +1+1+1+1)

Отношения последовательностей номеров разделов друг к другу

В Онлайн-энциклопедии целочисленных последовательностей (OEIS) последовательность обычных номеров разделов. $P(n)$ находится под кодом A000041, последовательность строгих разделов следующая. $Q(n)$ под кодом А000009 и последовательность суперразделов ${\overline {P}}(n)$ под кодом А015128. Все родительские разделы из индекса $n=1$ четные.

Последовательность суперразделов ${\overline {P}}(n)$ можно записать с помощью регулярной последовательности разбиения P и строгая последовательность разбиений Q можно сгенерировать следующим образом:

${\overline {P}}(n)=\sum _{k=0}^{n}P(n-k)Q(k)$

В следующей таблице последовательностей чисел эту формулу следует использовать в качестве примера:

н	П (п)	Q(n)	${\overline {P}}(n)$
0	1	1	1 = 1*1
1	1	1	2 = 1 * 1 + 1 * 1
2	2	1	4 = 2 * 1 + 1 * 1 + 1 * 1
3	3	2	8 = 3 * 1 + 2 * 1 + 1 * 1 + 1 * 2
4	5	2	14 = 5 * 1 + 3 * 1 + 2 * 1 + 1 * 2 + 1 * 2
5	7	3	24 = 7 * 1 + 5 * 1 + 3 * 1 + 2 * 2 + 1 * 2 + 1 * 3

также можно составить следующую комбинацию двух рядов сумм В связи с этим свойством с помощью функции ϑ ₀₁ :

$\theta _{4}(x)={\biggl [}\sum _{k=0}^{\infty }P(k)x^{k}{\biggr ]}^{-1}{\biggl [}\sum _{k=0}^{\infty }Q(k)x^{k}{\biggr ]}^{-1}$

Ссылки

• Абрамовиц, Милтон ; Стегун, Ирен А. (1964). Справочник по математическим функциям . Нью-Йорк: Dover Publications . сек. 16.27 и далее. ISBN  978-0-486-61272-0 .
• Ахиезер, Наум Ильич (1990) [1970]. Элементы теории эллиптических функций . AMS Переводы математических монографий. Том. 79. Провиденс, Род-Айленд: AMS . ISBN  978-0-8218-4532-5 .
• Фаркас, Гершель М .; Кра, Ирвин (1980). Римановы поверхности . Нью-Йорк: Springer-Verlag . гл. 6. ISBN  978-0-387-90465-8 . . (для лечения теты Римана)
• Харди, штат Джорджия ; Райт, Э.М. (1959). Введение в теорию чисел (4-е изд.). Оксфорд: Кларендон Пресс .
• Мамфорд, Дэвид (1983). Тата-лекции по Тэте I. Бостон: Биркхаузер . ISBN  978-3-7643-3109-2 .
• Пирпон, Джеймс (1959). Функции комплексной переменной . Нью-Йорк: Dover Publications .
• Раух, Гарри Э .; Фаркас, Гершель М. (1974). Тета-функции с приложениями к римановым поверхностям . Балтимор: Уильямс и Уилкинс . ISBN  978-0-683-07196-2 .
• Рейнхардт, Уильям П.; Уокер, Питер Л. (2010), «Тета-функции» , в Олвере, Фрэнке У.Дж .; Лозье, Дэниел М.; Буасверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям , издательство Кембриджского университета, ISBN  978-0-521-19225-5 , МР   2723248 .
• Уиттакер, ET ; Уотсон, Дж.Н. (1927). Курс современного анализа (4-е изд.). Кембридж: Издательство Кембриджского университета . гл. 21. -функций Якоби (история θ )

Дальнейшее чтение

• Фаркас, Гершель М. (2008). «Тэта-функции в комплексном анализе и теории чисел». В Аллади, Кришнасвами (ред.). Обзоры по теории чисел . Развитие математики. Том. 17. Шпрингер-Верлаг . стр. 57–87. ISBN  978-0-387-78509-7 . Збл   1206.11055 .
• Шенеберг, Бруно (1974). «IX. Тета-серия». Эллиптические модульные функции . Основные положения математических наук. Том 203. Шпрингер-Верлаг . стр. 203–226. ISBN  978-3-540-06382-7 .
• Акерман, Майкл (1 февраля 1979 г.). «О производящих функциях некоторых рядов Эйзенштейна». Математические Аннален . 244 (1): 75–81. дои : 10.1007/BF01420339 . S2CID   120045753 .

Гарри Раух с Гершелем М. Фаркасом: Тета-функции с применением к римановым поверхностям, Уильямс и Уилкинс, Балтимор, Мэриленд, 1974, ISBN   0-683-07196-3 .

• Чарльз Эрмит: О разрешении отчетов об уравнениях пятой степени, CR Acad. наук. Париж, № 11 марта 1858 г.

Внешние ссылки

• Моисеев Игорь. «Эллиптические функции для Matlab и Octave» .

Эта статья включает в себя материал из интегральных представлений тета-функций Якоби на сайте PlanetMath , который доступен под лицензией Creative Commons Attribution/Share-Alike License .