Отношения доза -ответ

Отношение и ответа или отношения воздействия и ответа описывает величину реакции организма как дозы функцию воздействия (или доз ) на стимул или стрессор (обычно химический веществ ) после определенного времени воздействия. ^{[ 1 ]} Отношения дозы -ответа могут быть описаны с помощью кривых дозы -ответа . Это объясняется далее в следующих разделах. Функция реакции стимула или кривая реакции стимула определяется более широко как ответ от любого типа стимула, не ограничиваясь химическими веществами.

Мотивация для изучения доза -ответ

Изучение реакции дозы и разработки моделей дозы -ответа занимает центральное место в определении «безопасных», «опасных» и (где соответствующие) полезные уровни и дозировки для лекарств, загрязняющих веществ, пищевых продуктов и других веществ, на которые люди или другие организмы подвергаются . Эти выводы часто являются основой для государственной политики. Агентство по охране окружающей среды США разработало обширное руководство и отчеты о моделировании и оценке доза -ответ, а также о программном обеспечении. ^{[ 2 ]} Управление по контролю за продуктами и лекарствами США также имеет руководство по выяснению отношений дозы и ответа ^{[ 3 ]} Во время разработки лекарств . Отношения реакции дозы могут использоваться у отдельных лиц или в популяциях. Поговорка Доза заставляет яд отражает, как небольшое количество токсина не оказывает существенного эффекта, в то время как большое количество может быть смертельным. Это отражает, как отношения дозы и ответа могут использоваться у людей. В популяциях отношения дозы и ответа могут описать, как влияют группы людей или организмов на разных уровнях воздействия. Отношения реакции дозы, моделируемые кривыми отклика дозы, широко используются в фармакологии и разработке лекарств. В частности, форма кривой дозы лекарственного средства (количественно определяется по параметрам EC50, NH и YMAX) отражает биологическую активность и силу препарата.

Пример стимулов и ответы

Некоторые примеры мер для отношений дозы и ответа показаны в приведенных ниже таблицах. Каждый сенсорный стимул соответствует конкретному сенсорному рецептору , например, никотиновый ацетилхолин рецептор для никотина или механорецептор для механического давления. Однако стимулы (такие как температура или излучение) могут также влиять на физиологические процессы за пределами ощущения (и даже дают измеримый ответ смерти). Ответы могут быть записаны как непрерывные данные (например, сила сокращения мышц) или дискретные данные (например, количество смертей).

Пример стимула		Цель
наркотиков / токсина Доза	Агонист (например , никотин , изопреналин )	Биохимические рецепторы , Ферменты , Транспортеры
	Антагонист (например , кетамин , пропранолол )
	Аллостерический модулятор (например, бензодиазепин )
Температура		Температурные рецепторы
Уровни звука		Волосовые клетки
Освещение/интенсивность света		Фоторецепторы
Механическое давление		Механорецепторы
Доза патогена (например, LPS )		n/a
радиации Интенсивность		n/a


Системный уровень	Пример ответа
Население ( эпидемиология )	Смерть, ^{[ 4 ]} потеря сознания
Организм /целое животное ( физиология )	Тяжесть поражения, ^{[ 4 ]} артериальное давление, ^{[ 4 ]} частота сердечных сокращений, степень движения, внимательность, ЭЭГ данные
Орган / ткань	Производство АТФ, пролиферация, сокращение мышц, производство желчи, гибель клеток
Клетка ( клеточная биология , биохимия )	Производство АТФ, кальциевые сигналы, морфология, митоз

Анализ и создание кривых доза -ответ

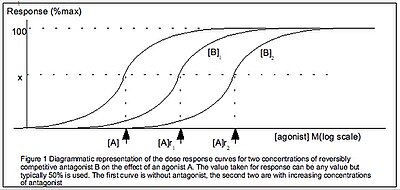
Строительство кривых доза -ответа

Кривая доза -ответ представляет собой координатный график, относящийся к величине дозы (стимула), с реакцией биологической системы. ряд эффектов (или конечных точек Может быть изучен ). Приложенная доза обычно нанесена на оси x, а отклик нанесен на ось Y. В некоторых случаях это логарифм дозы, построенной на оси x. Кривая обычно сигмоидальная , с самой крутой частью посередине. Биологические модели с использованием дозы предпочтительнее использования журнала (доза), потому что последний может визуально подразумевать пороговую дозу , когда на самом деле его нет. ^{[ Цитация необходима ]}

Статистический анализ кривых дозы -ответа может быть выполнен методами регрессии, такими как модель Probit или модель Logit , или другие методы, такие как метод Спирмена -Карбер. ^{[ 5 ]} Эмпирические модели, основанные на нелинейной регрессии, обычно предпочтительнее использования некоторого преобразования данных, которые линеаризуют взаимосвязь доза-ответ. ^{[ 6 ]}

Типичным экспериментальным дизайном для измерения взаимосвязи дозы-ответа являются препараты для ванны органов , анализы связывания лиганда , функциональные анализы и клинические исследования лекарств .

Специфическая для реакции на дозы радиации Общество физики здравоохранения (в Соединенных Штатах) опубликовало документальную серию о происхождении линейной модели NO-Throgold (LNT), хотя общество не приняло политику в отношении LNT ».

Уравнение холма

Кривые логарифмической дозы-ответа, как правило, являются сигмоидальной формой и монотонными и могут соответствовать классическому уравнению холма . Уравнение холма является логистической функцией относительно логарифма дозы и аналогично модели логита . Также была предложена обобщенная модель для многофазных случаев. ^{[ 7 ]}

Уравнение холма - это следующая формула, где $E$ величина ответа, ${\ce {[A]}}$ является ли концентрация препарата (или эквивалентно, интенсивность стимула) и $\mathrm {EC} _{50}$ концентрация лекарственного средства, которая дает максимальный ответ 50% и $n$ это коэффициент холма .

{\frac {E}{E_{\mathrm {max} }}}={\frac {[A]^{n}}{{\text{EC}}_{50}^{n}+[A]^{n}}}={\frac {1}{1+\left({\frac {\mathrm {EC} _{50}}{[A]}}\right)^{n}}}

^{[ 8 ]}

Параметры кривой отклика дозы отражают показатели эффективности (например, EC50, IC50, ED50 и т. Д.) И измерения эффективности (такие как ткань, клеточная или популяционная реакция).

Обычно используемая кривая доза -ответа представляет собой кривую EC ₅₀ , половина максимальной эффективной концентрации, где точка EC ₅₀ определяется как точка перегиба кривой.

Кривые отклика дозы обычно приспособлены к уравнению холма .

Первая точка вдоль графика, где достигается отклик выше нуля (или выше контрольного отклика), обычно называется пороговой дозой. Для большинства полезных или рекреационных препаратов желаемые эффекты обнаруживаются в дозах немного больше пороговой дозы. В более высоких дозах нежелательные побочные эффекты появляются и становятся сильнее по мере увеличения дозы. Чем более сильным является конкретное вещество, тем круче эта кривая. В количественных ситуациях ось Y часто обозначена процентами, которые относятся к проценту обнаженных лиц, регистрирующих стандартный ответ (который может быть смертью, как в LD ₅₀ ). Такая кривая называется квантовой кривой дозы -ответа, отличающей ее от кривой градуированной дозы -ответа, где ответ непрерывно (либо измерен, либо по решению).

Уравнение холма может быть использовано для описания отношений дозы и ответа, например, ионо-канала-откровенности по сравнению с концентрацией лиганда . ^{[ 9 ]}

Доза обычно находится в миллиграммах, микрограммах или граммах на килограмм взвешивания тела для воздействия полости рта или миллиграммов на кубический метр окружающего воздуха для воздействия вдыхания. Другие единицы дозы включают мосы на вес на тела, родинки на животное и для дермального воздействия, молей на квадратный сантиметр.

E _Max Model

Модель E _Max - это обобщение уравнения холма, где может быть установлен эффект для нулевой дозы. Используя ту же обозначения, что и выше, мы можем выразить модель как: ^{[ 10 ]}

E=E_{0}+{\frac {{[A]}^{n}\times {E_{\mathrm {max} }}}{{[A]}^{n}+\mathrm {EC} _{50}^{n}}}

Сравните с перестройкой холма:

E_{\mathrm {hill} }={\frac {{[A]}^{n}\times {E_{\mathrm {max} }}}{{[A]}^{n}+\mathrm {EC} _{50}^{n}}}

Модель E _Max является единственной наиболее распространенной моделью для описания взаимосвязи дозы-ответа в разработке лекарств. ^{[ 10 ]}

Форма кривой доза-ответа

Форма кривой доза-ответ обычно зависит от топологии целевой реакционной сети. В то время как форма кривой часто является монотонной , в некоторых случаях можно увидеть немонотонические кривые отклика дозы. ^{[ 11 ]}

Ограничения

Концепция линейных отношений дозы и ответа, порогов и ответов на все или ничего не может применяться к нелинейным ситуациям. Пороговая модель или линейная модель безпороговых значений может быть более подходящей, в зависимости от обстоятельств. Недавняя критика этих моделей, поскольку они применяются к эндокринным разрушителям, утверждает существенный пересмотр тестирования и токсикологических моделей в низких дозах из-за наблюдаемой не монотонности , IE U-образной дозы/ответа. ^{[ 12 ]}

Отношения доза -ответ обычно зависят от времени воздействия и пути воздействия (например, вдыхание, потребление питания); Количественная оценка ответа после другого времени воздействия или для другого пути приводит к другой взаимосвязи и, возможно, различным выводам о влиянии рассматриваемого стрессора. Это ограничение вызвано сложностью биологических систем и часто неизвестными биологическими процессами, действующими между внешним воздействием и побочным клеточным или тканевым ответом. ^{[ Цитация необходима ]}

Анализ щита

Анализ Шильда также может дать представление о влиянии лекарств.

Смотрите также

Ссылки

^ Crump, KS; Hoel, DG; Лэнгли, гл; Peto, R. (1 сентября 1976 г.). «Фундаментальные канцерогенные процессы и их последствия для оценки риска дозы» . РАНКА . 36 (9 Часть 1): 2973–2979. PMID 975067 .
^ Локхид Мартин (2009). Программное обеспечение Benchmark Dose (BMDS) версия 2.1 Руководство пользователя версии 2.0 (PDF) (проект изд.). Вашингтон, округ Колумбия: Агентство по охране окружающей среды США , Управление по охране окружающей среды.
^ «Отношения экспозиции и реагирование-дизайн исследования, анализ данных и регулирующие приложения» (PDF) . Управление по контролю за продуктами и лекарствами . 26 марта 2019 года.
^ Jump up to: ^а ^{беременный} ^в Altshuler, B (1981). «Моделирование отношений доза-ответ» . Перспективы здоровья окружающей среды . 42 : 23–7. doi : 10.1289/ehp.814223 . PMC 1568781 . PMID 7333256 .
^ Гамильтон, Массачусетс; Руссо, RC; Терстон, Р.В. (1977). «Тримменный метод Спирмена -Карбер для оценки средних летальных концентраций в биоанализах токсичности». Экологическая наука и технология . 11 (7): 714–9. Bibcode : 1977enst ... 11..714h . doi : 10.1021/es60130a004 .
^ Бейтс, Дуглас М.; Уоттс, Дональд Г. (1988). Нелинейный регрессионный анализ и его приложения . Уайли . п. 365. ISBN 9780471816430 .
^ Di Veroli, Giovanni Y.; Fornari, Chiara; Голдлуст, Ян; Миллс, Грэм; Ко, Сьян Бун; Bramhall, Jo L.; Ричардс, Фрэнсис М.; Джодрелл, Дункан I. (1 октября 2015 г.). «Процедура автоматической подгонки и программное обеспечение для кривых доза-ответа с многофазными функциями» . Научные отчеты . 5 (1): 14701. Bibcode : 2015natsr ... 514701V . doi : 10.1038/srep14701 . PMC 4589737 . PMID 26424192 .
^ Neubig, Richard R.; Спеддинг, Майкл; Кенакин, Терри; Кристопулос, Артур; Международный союз фармакологического комитета по номенклатуре и препаратам рецептора, классификация. (Декабрь 2003 г.). «Международный союз фармакологии по номенклатуре и классификации лекарств. XXXVIII. Фармакологические обзоры . 55 (4): 597–606. doi : 10.1124/pr.55.4.4 . PMID 14657418 . S2CID 1729572 .
^ Ding, S; Sachs, F (1999). «Одноканальные свойства P2X2 пуриноцепторов» . J. Gen. Physiol . 113 (5). Пресса Рокфеллерского университета: 695–720. doi : 10.1085/jgp.113.5.695 . PMC 2222910 . PMID 10228183 .
^ Jump up to: ^а ^{беременный} MacDougall, James (2006). «Анализ исследований доза -ответ - модель модели». Нахождение дозы в разработке лекарств . Статистика биологии и здоровья. С. 127–145. doi : 10.1007/0-387-33706-7_9 . ISBN 978-0-387-29074-4 .
^ Roeland van Wijk et al., Немонотоническая динамика и перекрестные помехи в сигнальных путях и их последствия для фармакологии. Scientific Reports 5: 11376 (2015) два : 10.1038/srep11376
^ Ванденберг, Лора Н.; Колборн, Тео; Хейс, Тайрон Б.; Хейндель, Джерролд Дж.; Джейкобс, Дэвид Р.; Ли, Duk-Hee; Шиода, Тоши; Сото, Ана М.; Vom Saal, Frederick S.; Welshons, Wade v.; Золлер Р. Томас; Майерс, Джон Петерсон (2012). «Гормоны и эндокринные химические вещества: эффекты низких доз и немонотонные дозы» . Эндокринные обзоры . 33 (3): 378–455. doi : 10.1210/er.2011-1050 . PMC 3365860 . PMID 22419778 .

Внешние ссылки

Онлайн -инструмент для анализа ELISA
Онлайн IC ₅₀ калькулятор
Ecotoxmodels Веб-сайт по математическим моделям в экотоксикологии , с акцентом на токсикокинетико-токсикодинамические модели
CDD Vault, пример программного обеспечения для подгонки кривой доза-ответ

[1] Crump, KS; Hoel, DG; Лэнгли, гл; Peto, R. (1 сентября 1976 г.). «Фундаментальные канцерогенные процессы и их последствия для оценки риска дозы» . РАНКА . 36 (9 Часть 1): 2973–2979. PMID 975067 .

[2] Локхид Мартин (2009). Программное обеспечение Benchmark Dose (BMDS) версия 2.1 Руководство пользователя версии 2.0 (PDF) (проект изд.). Вашингтон, округ Колумбия: Агентство по охране окружающей среды США , Управление по охране окружающей среды.

[3] «Отношения экспозиции и реагирование-дизайн исследования, анализ данных и регулирующие приложения» (PDF) . Управление по контролю за продуктами и лекарствами . 26 марта 2019 года.

[:0-4] Jump up to: ^а ^{беременный} ^в Altshuler, B (1981). «Моделирование отношений доза-ответ» . Перспективы здоровья окружающей среды . 42 : 23–7. doi : 10.1289/ehp.814223 . PMC 1568781 . PMID 7333256 .

[HamiltonRusso1977-5] Гамильтон, Массачусетс; Руссо, RC; Терстон, Р.В. (1977). «Тримменный метод Спирмена -Карбер для оценки средних летальных концентраций в биоанализах токсичности». Экологическая наука и технология . 11 (7): 714–9. Bibcode : 1977enst ... 11..714h . doi : 10.1021/es60130a004 .

[BatesWatts1988-6] Бейтс, Дуглас М.; Уоттс, Дональд Г. (1988). Нелинейный регрессионный анализ и его приложения . Уайли . п. 365. ISBN 9780471816430 .

[7] Di Veroli, Giovanni Y.; Fornari, Chiara; Голдлуст, Ян; Миллс, Грэм; Ко, Сьян Бун; Bramhall, Jo L.; Ричардс, Фрэнсис М.; Джодрелл, Дункан I. (1 октября 2015 г.). «Процедура автоматической подгонки и программное обеспечение для кривых доза-ответа с многофазными функциями» . Научные отчеты . 5 (1): 14701. Bibcode : 2015natsr ... 514701V . doi : 10.1038/srep14701 . PMC 4589737 . PMID 26424192 .

[Terms-8] Neubig, Richard R.; Спеддинг, Майкл; Кенакин, Терри; Кристопулос, Артур; Международный союз фармакологического комитета по номенклатуре и препаратам рецептора, классификация. (Декабрь 2003 г.). «Международный союз фармакологии по номенклатуре и классификации лекарств. XXXVIII. Фармакологические обзоры . 55 (4): 597–606. doi : 10.1124/pr.55.4.4 . PMID 14657418 . S2CID 1729572 .

[9] Ding, S; Sachs, F (1999). «Одноканальные свойства P2X2 пуриноцепторов» . J. Gen. Physiol . 113 (5). Пресса Рокфеллерского университета: 695–720. doi : 10.1085/jgp.113.5.695 . PMC 2222910 . PMID 10228183 .

[Emax-10] Jump up to: ^а ^{беременный} MacDougall, James (2006). «Анализ исследований доза -ответ - модель модели». Нахождение дозы в разработке лекарств . Статистика биологии и здоровья. С. 127–145. doi : 10.1007/0-387-33706-7_9 . ISBN 978-0-387-29074-4 .

[11] Roeland van Wijk et al., Немонотоническая динамика и перекрестные помехи в сигнальных путях и их последствия для фармакологии. Scientific Reports 5: 11376 (2015) два : 10.1038/srep11376

[VandenbergColborn2012-12] Ванденберг, Лора Н.; Колборн, Тео; Хейс, Тайрон Б.; Хейндель, Джерролд Дж.; Джейкобс, Дэвид Р.; Ли, Duk-Hee; Шиода, Тоши; Сото, Ана М.; Vom Saal, Frederick S.; Welshons, Wade v.; Золлер Р. Томас; Майерс, Джон Петерсон (2012). «Гормоны и эндокринные химические вещества: эффекты низких доз и немонотонные дозы» . Эндокринные обзоры . 33 (3): 378–455. doi : 10.1210/er.2011-1050 . PMC 3365860 . PMID 22419778 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]