- ₇ многогранник

Орфографические проекции
Самолет ₇ Коксетера
7-симплекс

В семимерной геометрии существует 71 однородный многогранник с _A7 симметрией . Существует одна самодвойственная правильная форма — 7-симплекс с 8 вершинами.

Каждую из них можно визуализировать как симметричные ортогональные проекции в плоскостях Кокстера группы А ₇ Кокстера и других подгрупп.

Графики

Симметричные ортогональные проекции этих 71 многогранника можно построить в _A7 , _A6 , _A5 , _A4 , _A3 , _A2 плоскостях Кокстера . A _k имеет [k+1] симметрию . Для четных k и симметричных кольцевых диаграмм симметрия удваивается до [2(k+1)] .

Каждый из этих 71 многогранника показан в этих 6 плоскостях симметрии, с нарисованными вершинами и ребрами, а вершины окрашены в соответствии с количеством перекрывающихся вершин в каждой проективной позиции.

#	Диаграмма Кокстера-Динкина Символ Шлефли Имя Джонсона	A _k ортогональных проекций графы
#	Диаграмма Кокстера-Динкина Символ Шлефли Имя Джонсона	A ₇ [8]	А ₆ [7]	A_А5 [6]	A ₄ [5]	A_А3 [4]	A_А2 [3]
1	т ₀ {3,3,3,3,3,3} 7-симплекс
2	т ₁ {3,3,3,3,3,3} Выпрямленный 7-симплекс
3	т ₂ {3,3,3,3,3,3} Биректифицированный 7-симплекс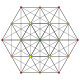
4	т ₃ {3,3,3,3,3,3} Триректифицированный 7-симплекс
5	т _0,1 {3.3.3.3.3.3} Усеченный 7-симплекс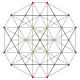
6	т _0,2 {3.3.3.3.3.3} Кантеллированный 7-симплекс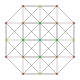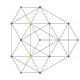
7	т _1,2 {3,3,3,3,3,3} Битусеченный 7-симплекс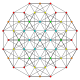
8	т _0,3 {3.3.3.3.3.3} Ранцинированный 7-симплекс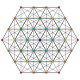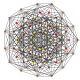
9	т _1,3 {3,3,3,3,3,3} Двукантельчатый 7-симплекс
10	т _2,3 {3,3,3,3,3,3} Трехусеченный 7-симплекс
11	т _0,4 {3.3.3.3.3.3} Стерический 7-симплекс
12	т _1,4 {3,3,3,3,3,3} Бирунцированный 7-симплекс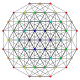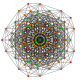
13	т _2,4 {3,3,3,3,3,3} Треугольный 7-симплекс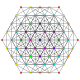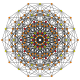
14	т _0,5 {3,3,3,3,3,3} Пятеричный 7-симплекс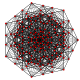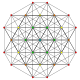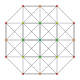
15	т _1,5 {3,3,3,3,3,3} Бистерифицированный 7-симплекс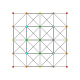
16	т _0,6 {3.3.3.3.3.3} Шестигранный 7-симплекс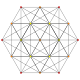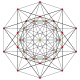
17	т _0,1,2 {3,3,3,3,3,3} Количественно усеченный 7-симплекс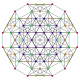
18	т _0,1,3 {3,3,3,3,3,3} Ранцитусеченный 7-симплекс
19	т _0,2,3 {3,3,3,3,3,3} Рунцикантеллярный 7-симплекс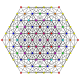
20	т _1,2,3 {3,3,3,3,3,3} Бикантиусеченный 7-симплекс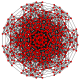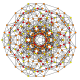
21	т _0,1,4 {3,3,3,3,3,3} Стеритусеченный 7-симплекс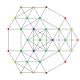
22	т _0,2,4 {3,3,3,3,3,3} Стерикантеллированный 7-симплекс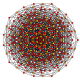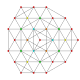
23	т _1,2,4 {3,3,3,3,3,3} Бирюроусеченный 7-симплекс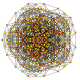
24	т _0,3,4 {3,3,3,3,3,3} Стерильный 7-симплекс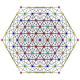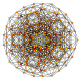
25	т _1,3,4 {3,3,3,3,3,3} Бирунчикантеллированный 7-симплекс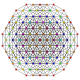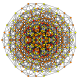
26	т _2,3,4 {3,3,3,3,3,3} Трикантиусеченный 7-симплекс
27	т _0,1,5 {3,3,3,3,3,3} Пятиусеченный 7-симплекс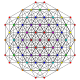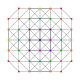
28	т _0,2,5 {3,3,3,3,3,3} Пятиконтеллярный 7-симплекс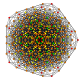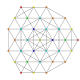
29	т _1,2,5 {3,3,3,3,3,3} Бистериусеченный 7-симплекс
30	т _0,3,5 {3,3,3,3,3,3} Пятислойный 7-симплекс
31	т _1,3,5 {3,3,3,3,3,3} Бистерикантеллированный 7-симплекс
32	т _0,4,5 {3,3,3,3,3,3} Пентистерифицированный 7-симплекс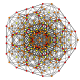
33	т _0,1,6 {3,3,3,3,3,3} Шестиусеченный 7-симплекс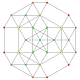
34	т _0,2,6 {3,3,3,3,3,3} Шестикантеллярный 7-симплекс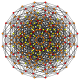
35	т _0,3,6 {3,3,3,3,3,3} Шестиструнный 7-симплекс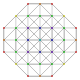
36	т _0,1,2,3 {3,3,3,3,3,3} Ранчикантиусеченный 7-симплекс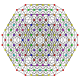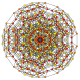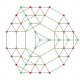
37	т _0,1,2,4 {3,3,3,3,3,3} Стерикантиусеченный 7-симплекс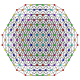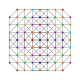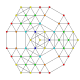
38	т _0,1,3,4 {3,3,3,3,3,3} Стерильный усеченный 7-симплекс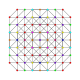
39	т _0,2,3,4 {3,3,3,3,3,3} Стерирунцикантеллярный 7-симплекс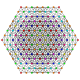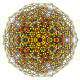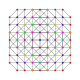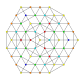
40	т _1,2,3,4 {3,3,3,3,3,3} Бирюнцикантиусеченный 7-симплекс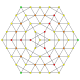
41	т _0,1,2,5 {3,3,3,3,3,3} Пентикантиусеченный 7-симплекс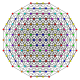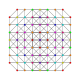
42	т _0,1,3,5 {3,3,3,3,3,3} Пятикруглый усеченный 7-симплекс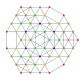
43	т _0,2,3,5 {3,3,3,3,3,3} Пятирунчикантеллированный 7-симплекс
44	т _1,2,3,5 {3,3,3,3,3,3} Бистерический усеченный 7-симплекс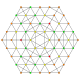
45	т _0,1,4,5 {3,3,3,3,3,3} Пентистеритусеченный 7-симплекс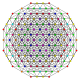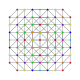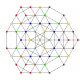
46	т _0,2,4,5 {3,3,3,3,3,3} Пентистерикантеллированный 7-симплекс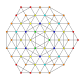
47	т _1,2,4,5 {3,3,3,3,3,3} Бистерирунцитусеченный 7-симплекс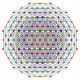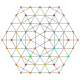
48	т _0,3,4,5 {3,3,3,3,3,3} Пентистерирцинтированный 7-симплекс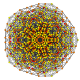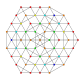
49	т _0,1,2,6 {3,3,3,3,3,3} Гексикантиусеченный 7-симплекс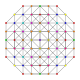
50	т _0,1,3,6 {3,3,3,3,3,3} Шестиусеченный 7-симплекс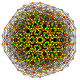
51	т _0,2,3,6 {3,3,3,3,3,3} Шестигранникантеллированный 7-симплекс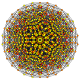
52	т _0,1,4,6 {3,3,3,3,3,3} Гексистериусеченный 7-симплекс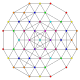
53	т _0,2,4,6 {3,3,3,3,3,3} Гексистерикантеллированный 7-симплекс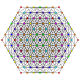
54	т _0,1,5,6 {3,3,3,3,3,3} Гексипентиусеченный 7-симплекс
55	т _0,1,2,3,4 {3,3,3,3,3,3} Стерирунцикантиусеченный 7-симплекс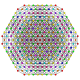
56	т _0,1,2,3,5 {3,3,3,3,3,3} Пентирунсикантиусеченный 7-симплекс
57	т _0,1,2,4,5 {3,3,3,3,3,3} Пентистерикантиусеченный 7-симплекс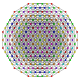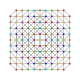
58	т _0,1,3,4,5 {3,3,3,3,3,3} Пентистерирундусеченный 7-симплекс
59	т _0,2,3,4,5 {3,3,3,3,3,3} Пентистерирунцикантеллярный 7-симплекс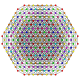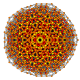
60	т _1,2,3,4,5 {3,3,3,3,3,3} Бистерирунцикантиусеченный 7-симплекс
61	т _0,1,2,3,6 {3,3,3,3,3,3} Шестигранно-усеченный 7-симплекс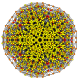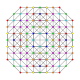
62	т _0,1,2,4,6 {3,3,3,3,3,3} Гексистерический усеченный 7-симплекс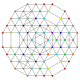
63	т _0,1,3,4,6 {3,3,3,3,3,3} Гексистерирундусеченный 7-симплекс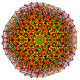
64	т _0,2,3,4,6 {3,3,3,3,3,3} Гексистерирунчикантеллированный 7-симплекс
65	т _0,1,2,5,6 {3,3,3,3,3,3} Гексипентикантитусеченный 7-симплекс
66	т _0,1,3,5,6 {3,3,3,3,3,3} Шестипериусеченный 7-симплекс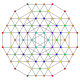
67	т _0,1,2,3,4,5 {3,3,3,3,3,3} Пентистерирунцикантиусеченный 7-симплекс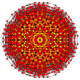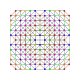
68	т _0,1,2,3,4,6 {3,3,3,3,3,3} Гексистерирунсикантиусеченный 7-симплекс
69	т _0,1,2,3,5,6 {3,3,3,3,3,3} Гексипентирунсикантиусеченный 7-симплекс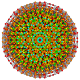
70	т _0,1,2,4,5,6 {3,3,3,3,3,3} Гексипентистерикантиусеченный 7-симплекс
71	т _{0,1,2,3,4,5,6} {3,3,3,3,3,3} Всеусеченный 7-симплекс

Ссылки

ХСМ Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 ^[1]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380–407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
Клитцинг, Ричард. «7D однородные многогранники (полиекса)» .

Примечания

^ Wiley:: Калейдоскопы: Избранные сочинения HSM Коксетера

v т и Фундаментальные выпуклые правильные и однородные многогранники размерностей 2–10.
Семья	н	Б _н	И ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ж ₄ / Г ₂	Ч _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16 ячеек • Тессеракт	Демитессеракт	24-ячеечный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Равномерный n - многогранник	n - симплекс	n - ортоплекс • n - куб	n - демикуб	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений.

[1] Wiley:: Калейдоскопы: Избранные сочинения HSM Коксетера

[1]