Выпуклая функция

Выпуклая функция на интервале .

Функция (черный цвет) является выпуклой тогда и только тогда, когда область над ее графиком (зеленый цвет) представляет собой выпуклое множество .

График двумерной выпуклой функции x ² + ху + у ² .

Выпуклый против невыпуклого

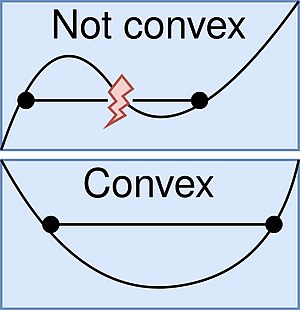
В математике называется действительная функция выпуклой , если отрезок между любыми двумя различными точками на графике функции лежит над графиком между двумя точками. Аналогично, функция является выпуклой, если ее надграфик (множество точек на графике функции или над ним) представляет собой выпуклое множество . Проще говоря, график выпуклой функции имеет форму чашки. $\cup$ (или прямую линию, как у линейной функции), а график вогнутой функции имеет форму шапки $\cap$.

Дважды дифференцируемая функция одной переменной является выпуклой тогда и только тогда, когда ее вторая производная неотрицательна во всей области определения . К хорошо известным примерам выпуклых функций одной переменной относится линейная функция $f(x)=cx$ (где $c$ ) действительное число , квадратичная функция $cx^{2}$ ( $c$ как неотрицательное действительное число) и показательную функцию $ce^{x}$ ( $c$ как неотрицательное действительное число).

Выпуклые функции играют важную роль во многих областях математики. Они особенно важны при исследовании задач оптимизации , где отличаются рядом удобных свойств. Например, строго выпуклая функция на открытом множестве имеет не более одного минимума . Даже в бесконечномерных пространствах при подходящих дополнительных гипотезах выпуклые функции продолжают удовлетворять таким свойствам и в результате являются наиболее хорошо изученными функционалами в вариационном исчислении . В теории вероятностей выпуклая функция, примененная к ожидаемому значению всегда случайной величины, ограничена сверху ожидаемым значением выпуклой функции случайной величины. Этот результат, известный как неравенство Йенсена , может быть использован для вывода таких неравенств , как среднее арифметико-геометрическое неравенство и неравенство Гёльдера .

Определение

Визуализация выпуклой функции и неравенства Йенсена

Позволять $X$ — выпуклое подмножество вещественного векторного пространства и пусть $f:X\to \mathbb {R}$ быть функцией.

Затем $f$ называется выпуклым тогда и только тогда, когда выполняется любое из следующих эквивалентных условий:

1. Для всех $0\leq t\leq 1$ и все $x_{1},x_{2}\in X$: $$f\left(tx_{1}+(1-t)x_{2}\right)\leq tf\left(x_{1}\right)+(1-t)f\left(x_{2}\right)$$Правая часть представляет собой прямую линию между $\left(x_{1},f\left(x_{1}\right)\right)$ и $\left(x_{2},f\left(x_{2}\right)\right)$ на графике $f$ как функция $t;$ увеличение $t$ от $0$ к $1$ или уменьшение $t$ от $1$ к $0$ сметает эту линию. Аналогично, аргумент функции $f$ в левой части представляет собой прямую линию между $x_{1}$ и $x_{2}$ в $X$ или $x$-ось графика $f.$ Итак, это условие требует, чтобы прямая между любой парой точек кривой $f$ быть выше или просто соответствует графику.
2. Для всех $0<t<1$ и все $x_{1},x_{2}\in X$ такой, что $x_{1}\neq x_{2}$: $$f\left(tx_{1}+(1-t)x_{2}\right)\leq tf\left(x_{1}\right)+(1-t)f\left(x_{2}\right)$$Отличие этого второго условия от первого условия выше состоит в том, что это условие не включает точки пересечения (например, $\left(x_{1},f\left(x_{1}\right)\right)$ и $\left(x_{2},f\left(x_{2}\right)\right)$) между прямой, проходящей через пару точек кривой $f$ (прямая линия представлена ​​правой частью этого условия) и кривая $f;$ первое условие включает точки пересечения, когда оно становится $f\left(x_{1}\right)\leq f\left(x_{1}\right)$ или $f\left(x_{2}\right)\leq f\left(x_{2}\right)$ в $t=0$ или $1,$ или $x_{1}=x_{2}.$ На самом деле точки пересечения не обязательно рассматривать в состоянии выпуклости, используя $$f\left(tx_{1}+(1-t)x_{2}\right)\leq tf\left(x_{1}\right)+(1-t)f\left(x_{2}\right)$$ потому что $f\left(x_{1}\right)\leq f\left(x_{1}\right)$ и $f\left(x_{2}\right)\leq f\left(x_{2}\right)$ всегда истинны (поэтому бесполезно быть частью условия).

Второе утверждение, характеризующее выпуклые функции, оцениваемые в действительной строке $\mathbb {R}$ это также оператор, используемый для определения выпуклых функций , которые оцениваются в расширенной строке действительных чисел. $[-\infty ,\infty ]=\mathbb {R} \cup \{\pm \infty \},$ где такая функция $f$ разрешено брать $\pm \infty$ как ценность. Первый оператор не используется, поскольку он позволяет $t$ взять $0$ или $1$ как значение, и в этом случае, если $f\left(x_{1}\right)=\pm \infty$ или $f\left(x_{2}\right)=\pm \infty ,$ соответственно, тогда $tf\left(x_{1}\right)+(1-t)f\left(x_{2}\right)$ будет неопределенным (поскольку умножения $0\cdot \infty$ и $0\cdot (-\infty )$ не определены). Сумма $-\infty +\infty$ также не определено, поэтому выпуклой расширенной функции с действительным знаком обычно разрешено принимать только одно из $-\infty$ и $+\infty$ как ценность.

Второе утверждение также можно изменить, чтобы получить определение строгой выпуклости , где последнее получается заменой $\,\leq \,$ при строгом неравенстве $\,<.$ Явно карта $f$ называется строго выпуклым тогда и только тогда, когда для всех действительных $0<t<1$ и все $x_{1},x_{2}\in X$ такой, что $x_{1}\neq x_{2}$: $$f\left(tx_{1}+(1-t)x_{2}\right)<tf\left(x_{1}\right)+(1-t)f\left(x_{2}\right)$$

Строго выпуклая функция $f$ — это функция, согласно которой прямая линия между любой парой точек кривой $f$ находится над кривой $f$ за исключением точек пересечения прямой и кривой. Пример функции, которая является выпуклой, но не строго выпуклой: $f(x,y)=x^{2}+y$. Эта функция не является строго выпуклой, поскольку между любыми двумя точками, имеющими общую координату x, будет прямая линия, а любые две точки, НЕ имеющие общую координату x, будут иметь большее значение функции, чем точки между ними.

Функция $f$ называется вогнутым (соответственно строго вогнутым ), если $-f$ ( $f$ умноженный на −1), является выпуклым (соответственно строго выпуклым).

Альтернативное наименование

Термин «выпуклый» часто называют « выпуклым вниз» или «вогнутым вверх» , а термин «вогнутый» часто называют «вогнутым вниз» или «выпуклым вверх» . Если термин «выпуклый» используется без ключевых слов «вверх» или «вниз», то он относится строго к графику в форме чаши. $\cup$. Например, неравенство Йенсена относится к неравенству, включающему выпуклую или выпуклую (вниз) функцию.

Характеристики

Многие свойства выпуклых функций имеют для функций многих переменных такую ​​же простую формулировку, как и для функций одной переменной. Ниже приведены свойства для случая многих переменных, так как некоторые из них не указаны для функций одной переменной.

Функции одной переменной

• Предполагать $f$ является функцией одной действительной переменной, определенной на интервале, и пусть $$R(x_{1},x_{2})={\frac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}$$ (Обратите внимание, что $R(x_{1},x_{2})$ — наклон фиолетовой линии на первом рисунке; функция $R$ симметричен ​ в $(x_{1},x_{2}),$ означает, что $R$ не меняется при обмене $x_{1}$ и $x_{2}$). $f$ выпукло тогда и только тогда, когда $R(x_{1},x_{2})$ монотонно не убывает по $x_{1},$ за каждое фиксированное $x_{2}$ (или наоборот). Эта характеристика выпуклости весьма полезна для доказательства следующих результатов.
• Выпуклая функция $f$ одной действительной переменной, определенной на некотором открытом интервале $C$ постоянно ​ включен $C.$ $f$ допускает левые и правые производные , причем они монотонно не убывают . Кроме того, левая производная непрерывна слева, а правая производная непрерывна справа. Как следствие, $f$ дифференцируемо во всех точках , кроме не более чем счетного числа , множество, в которых $f$ не дифференцируемо, однако может быть плотным. Если $C$ закрыто, то $f$ может перестать быть непрерывным в конечных точках $C$ (пример показан в разделе примеры ).
• Дифференцируемая производная функция одной переменной выпукла на отрезке тогда и только тогда, когда ее монотонно не убывает на этом отрезке. Если функция дифференцируема и выпукла, то она также непрерывно дифференцируема .
• Дифференцируемая функция одной переменной выпукла на отрезке тогда и только тогда, когда ее график лежит выше всех ее касательных : $$f(x)\geq f(y)+f'(y)(x-y)$$ для всех $x$ и $y$ в интервале.
• Дважды дифференцируемая функция одной переменной выпукла на отрезке тогда и только тогда, когда ее вторая производная на этом интервале неотрицательна; это дает практический тест на выпуклость. Визуально дважды дифференцируемая выпуклая функция «выгибается вверх», без каких-либо изгибов в другую сторону ( точки перегиба ). Если ее вторая производная положительна во всех точках, то функция строго выпуклая, но обратное неверно. Например, вторая производная от $f(x)=x^{4}$ является $f''(x)=12x^{2}$, что равно нулю для $x=0,$ но $x^{4}$ является строго выпуклым.
  • Это свойство и указанное выше свойство в терминах «...его производная монотонно не убывает...» не равны, поскольку если $f''$ неотрицательна на интервале $X$ затем $f'$ монотонно не убывает на $X$ а обратное неверно, например, $f'$ монотонно не убывает на $X$ в то время как его производная $f''$ не определен в некоторых точках $X$.
• Если $f$ является выпуклой функцией одной действительной переменной, а $f(0)\leq 0$, затем $f$ является супераддитивным на положительных действительных числах , то есть $f(a+b)\geq f(a)+f(b)$ для положительных действительных чисел $a$ и $b$.

Доказательство

С $f$ является выпуклой, используя одно из приведенных выше определений выпуклой функции и позволяя $x_{2}=0,$ отсюда следует, что для всех реальных $0\leq t\leq 1,$ $${\begin{aligned}f(tx_{1})&=f(tx_{1}+(1-t)\cdot 0)\\&\leq tf(x_{1})+(1-t)f(0)\\&\leq tf(x_{1}).\\\end{aligned}}$$ От $f(tx_{1})\leq tf(x_{1})$, отсюда следует, что $${\begin{aligned}f(a)+f(b)&=f\left((a+b){\frac {a}{a+b}}\right)+f\left((a+b){\frac {b}{a+b}}\right)\\&\leq {\frac {a}{a+b}}f(a+b)+{\frac {b}{a+b}}f(a+b)\\&=f(a+b).\\\end{aligned}}$$ А именно, $f(a)+f(b)\leq f(a+b)$.

• Функция $f$ является выпуклой средней точкой на интервале $C$ если для всех $x_{1},x_{2}\in C$ $$f\!\left({\frac {x_{1}+x_{2}}{2}}\right)\leq {\frac {f(x_{1})+f(x_{2})}{2}}.$$ Это условие лишь немного слабее выпуклости. Например, действительнозначная измеримая функция Лебега , выпуклая в средней точке, является выпуклой: это теорема Серпинского . В частности, непрерывная функция, выпуклая в средней точке, будет выпуклой.

Функции нескольких переменных

• Функция, которая незначительно выпукла по каждой отдельной переменной, не обязательно (совместно) выпукла. Например, функция $f(x,y)=xy$ является маргинально линейным и, следовательно, маргинально выпуклым по каждой переменной, но не (совместно) выпуклым.
• Функция $f:X\to [-\infty ,\infty ]$ оценивается в расширенных действительных числах $[-\infty ,\infty ]=\mathbb {R} \cup \{\pm \infty \}$ выпукло тогда и только тогда, когда его надграфик $$\{(x,r)\in X\times \mathbb {R} ~:~r\geq f(x)\}$$ представляет собой выпуклое множество.
• Дифференцируемая функция $f$ определенное на выпуклой области, является выпуклым тогда и только тогда, когда $f(x)\geq f(y)+\nabla f(y)^{T}\cdot (x-y)$ держится для всех $x,y$ в домене.
• Дважды дифференцируемая функция нескольких переменных является выпуклой на выпуклом множестве тогда и только тогда, когда ее матрица Гессе вторых частных производных положительно полуопределена внутри выпуклого множества.
• Для выпуклой функции $f,$ наборы подуровней $\{x:f(x)<a\}$ и $\{x:f(x)\leq a\}$ с $a\in \mathbb {R}$ являются выпуклыми множествами. Функция, удовлетворяющая этому свойству, называется квазивыпуклой функцией и может не быть выпуклой функцией.
• Следовательно, множество глобальных минимизаторов выпуклой функции $f$ представляет собой выпуклое множество: ${\operatorname {argmin} }\,f$ - выпуклый.
• Любой локальный минимум выпуклой функции также является глобальным минимумом . выпуклая функция Строго будет иметь не более одного глобального минимума.
• Неравенство Йенсена применимо к любой выпуклой функции. $f$. Если $X$ – случайная величина, принимающая значения в области $f,$ затем $\operatorname {E} (f(X))\geq f(\operatorname {E} (X)),$ где $\operatorname {E}$ обозначает математическое ожидание . Действительно, выпуклые функции — это именно те, которые удовлетворяют гипотезе неравенства Йенсена .
• первого порядка Однородная функция двух положительных переменных $x$ и $y,$ (то есть функция, удовлетворяющая $f(ax,ay)=af(x,y)$ за все позитивное настоящее $a,x,y>0$), выпуклый по одной переменной, должен быть выпуклым по другой переменной.

Операции, сохраняющие выпуклость

• $-f$ вогнута тогда и только тогда, когда $f$ является выпуклым.
• Если $r$ тогда любое действительное число $r+f$ выпукло тогда и только тогда, когда $f$ является выпуклым.
• Неотрицательные взвешенные суммы:
  • если $w_{1},\ldots ,w_{n}\geq 0$ и $f_{1},\ldots ,f_{n}$ все выпуклые, то и $w_{1}f_{1}+\cdots +w_{n}f_{n}.$ В частности, сумма двух выпуклых функций выпукла.
  • это свойство распространяется также на бесконечные суммы, интегралы и ожидаемые значения (при условии, что они существуют).
• Поэлементный максимум: пусть $\{f_{i}\}_{i\in I}$ быть набором выпуклых функций. Затем $g(x)=\sup \nolimits _{i\in I}f_{i}(x)$ является выпуклым. Домен $g(x)$ представляет собой совокупность точек, в которых выражение конечно. Важные особые случаи:
  • Если $f_{1},\ldots ,f_{n}$ являются выпуклыми функциями, то так же $g(x)=\max \left\{f_{1}(x),\ldots ,f_{n}(x)\right\}.$
  • Теорема Данскина : если $f(x,y)$ является выпуклым в $x$ затем $g(x)=\sup \nolimits _{y\in C}f(x,y)$ является выпуклым в $x$ даже если $C$ не является выпуклым множеством.
• Состав:
  • Если $f$ и $g$ являются выпуклыми функциями и $g$ не убывает в одномерной области, то $h(x)=g(f(x))$ является выпуклым. Например, если $f$ выпукло, то и так $e^{f(x)}$ потому что $e^{x}$ выпукло и монотонно возрастает.
  • Если $f$ является вогнутым и $g$ выпукло и не возрастает в одномерной области, то $h(x)=g(f(x))$ является выпуклым.
  • Выпуклость инвариантна относительно аффинных отображений: т.е. если $f$ выпукло с областью определения $D_{f}\subseteq \mathbf {R} ^{m}$, тогда так и есть $g(x)=f(Ax+b)$, где $A\in \mathbf {R} ^{m\times n},b\in \mathbf {R} ^{m}$ с доменом $D_{g}\subseteq \mathbf {R} ^{n}.$
• Минимизация: Если $f(x,y)$ является выпуклым в $(x,y)$ затем $g(x)=\inf \nolimits _{y\in C}f(x,y)$ является выпуклым в $x,$ при условии, что $C$ является выпуклым множеством и что $g(x)\neq -\infty .$
• Если $f$ выпукло, то его перспектива $g(x,t)=tf\left({\tfrac {x}{t}}\right)$ с доменом $\left\{(x,t):{\tfrac {x}{t}}\in \operatorname {Dom} (f),t>0\right\}$ является выпуклым.
• Позволять $X$ быть векторным пространством. $f:X\to \mathbf {R}$ является выпуклым и удовлетворяет $f(0)\leq 0$ тогда и только тогда, когда $f(ax+by)\leq af(x)+bf(y)$ для любого $x,y\in X$ и любые неотрицательные действительные числа $a,b$ которые удовлетворяют $a+b\leq 1.$

Сильно выпуклые функции

Понятие сильной выпуклости расширяет и параметризует понятие строгой выпуклости. Интуитивно понятно, что сильно выпуклая функция — это функция, которая растет так же быстро, как квадратичная функция. Сильно выпуклая функция является также строго выпуклой, но не наоборот. Если одномерная функция $f$ дважды непрерывно дифференцируема и областью определения является действительная прямая, то мы можем охарактеризовать ее следующим образом:

• $f$ выпукло тогда и только тогда, когда $f''(x)\geq 0$ для всех $x.$
• $f$ строго выпуклая, если $f''(x)>0$ для всех $x$ (примечание: этого достаточно, но не обязательно).
• $f$ сильно выпуклая тогда и только тогда, когда $f''(x)\geq m>0$ для всех $x.$

Например, пусть $f$ быть строго выпуклой, и пусть существует последовательность точек $(x_{n})$ такой, что $f''(x_{n})={\tfrac {1}{n}}$. Несмотря на то $f''(x_{n})>0$, функция не является сильно выпуклой, поскольку $f''(x)$ станет сколь угодно малым.

В более общем смысле, дифференцируемая функция $f$ называется сильно выпуклым с параметром $m>0$ если для всех точек выполнено неравенство $x,y$ в своем домене: $$(\nabla f(x)-\nabla f(y))^{T}(x-y)\geq m\|x-y\|_{2}^{2}$$или, в более общем смысле, $$\langle \nabla f(x)-\nabla f(y),x-y\rangle \geq m\|x-y\|^{2}$$где $\langle \cdot ,\cdot \rangle$ это любой внутренний продукт , и $\|\cdot \|$ является соответствующей нормой . Некоторые авторы, например назовем функции, удовлетворяющие этому неравенству, эллиптическими функциями.

Эквивалентным условием является следующее: $$f(y)\geq f(x)+\nabla f(x)^{T}(y-x)+{\frac {m}{2}}\|y-x\|_{2}^{2}$$

Чтобы функция была сильно выпуклой, не обязательно быть дифференцируемой. Третье определение для сильно выпуклой функции с параметром $m,$ это для всех $x,y$ в домене и $t\in [0,1],$$$f(tx+(1-t)y)\leq tf(x)+(1-t)f(y)-{\frac {1}{2}}mt(1-t)\|x-y\|_{2}^{2}$$

Обратите внимание, что это определение приближается к определению строгой выпуклости как $m\to 0,$ и идентично определению выпуклой функции, когда $m=0.$ Несмотря на это, существуют функции, строго выпуклые, но не сильно выпуклые ни при каких условиях. $m>0$ (см. пример ниже).

Если функция $f$ дважды непрерывно дифференцируема, то она сильно выпукла с параметром $m$ тогда и только тогда, когда $\nabla ^{2}f(x)\succeq mI$ для всех $x$ в домене, где $I$ это личность и $\nabla ^{2}f$ – матрица Гессе , а неравенство $\succeq$ означает, что $\nabla ^{2}f(x)-mI$ является положительно полуопределенным . Это эквивалентно требованию, чтобы минимальное собственное значение $\nabla ^{2}f(x)$ быть по крайней мере $m$ для всех $x.$ Если домен — это просто реальная линия, то $\nabla ^{2}f(x)$ это просто вторая производная $f''(x),$ таким образом, условие становится $f''(x)\geq m$. Если $m=0$ тогда это означает, что гессиан положительно полуопределен (или, если областью определения является действительная линия, это означает, что $f''(x)\geq 0$), откуда следует, что функция выпуклая и, возможно, строго выпуклая, но не сильно выпуклая.

Полагая еще, что функция дважды непрерывно дифференцируема, можно показать, что нижняя граница $\nabla ^{2}f(x)$ следует, что оно сильно выпуклое. Используя теорему Тейлора, существует $$z\in \{tx+(1-t)y:t\in [0,1]\}$$такой, что $$f(y)=f(x)+\nabla f(x)^{T}(y-x)+{\frac {1}{2}}(y-x)^{T}\nabla ^{2}f(z)(y-x)$$Затем $$(y-x)^{T}\nabla ^{2}f(z)(y-x)\geq m(y-x)^{T}(y-x)$$по предположению о собственных значениях, и, следовательно, мы восстанавливаем второе уравнение сильной выпуклости, приведенное выше.

Функция $f$ является сильно выпуклой с параметром m тогда и только тогда, когда функция $$x\mapsto f(x)-{\frac {m}{2}}\|x\|^{2}$$является выпуклым.

Дважды непрерывно дифференцируемая функция $f$ на компактном домене $X$ это удовлетворяет $f''(x)>0$ для всех $x\in X$ является сильно выпуклым. Доказательство этого утверждения следует из теоремы о крайних значениях , которая утверждает, что непрерывная функция на компакте имеет максимум и минимум.

С сильно выпуклыми функциями обычно легче работать, чем с выпуклыми или строго выпуклыми функциями, поскольку они представляют собой меньший класс. Как и строго выпуклые функции, сильно выпуклые функции имеют единственные минимумы на компактах.

Свойства сильно выпуклых функций

Если f — сильно выпуклая функция с параметром m , то:

• Для каждого действительного числа r уровней набор { x | ж ( Икс ) ≤ р } компактен .
• Функция f имеет единственный глобальный минимум на R ^н .

Равномерно выпуклые функции

Равномерно выпуклая функция, с модулем $\phi$, является функцией $f$ что для всех $x,y$ в домене и $t\in [0,1],$ удовлетворяет $$f(tx+(1-t)y)\leq tf(x)+(1-t)f(y)-t(1-t)\phi (\|x-y\|)$$где $\phi$ — функция, которая неотрицательна и обращается в нуль только в точке 0. Это обобщение понятия сильно выпуклой функции; взяв $\phi (\alpha )={\tfrac {m}{2}}\alpha ^{2}$ мы восстанавливаем определение сильной выпуклости.

Стоит отметить, что некоторые авторы требуют модуль $\phi$ быть возрастающей функцией, но этого условия требуют не все авторы.

Примеры

Функции одной переменной

• Функция $f(x)=x^{2}$ имеет $f''(x)=2>0$, поэтому f — выпуклая функция. Он также сильно выпуклый (а значит, и строго выпуклый) с сильной константой выпуклости 2.
• Функция $f(x)=x^{4}$ имеет $f''(x)=12x^{2}\geq 0$, поэтому f — выпуклая функция. Он строго выпуклый, хотя вторая производная не во всех точках строго положительна. Он не сильно выпуклый.
• Функция значения абсолютного $f(x)=|x|$ является выпуклым (что отражено в неравенстве треугольника ), даже если оно не имеет производной в точке $x=0.$ Он не является строго выпуклым.
• Функция $f(x)=|x|^{p}$ для $p\geq 1$ является выпуклым.
• Показательная функция $f(x)=e^{x}$ является выпуклым. Оно также строго выпукло, поскольку $f''(x)=e^{x}>0$, но он не является сильно выпуклым, поскольку вторая производная может быть сколь угодно близкой к нулю. В более общем смысле функция $g(x)=e^{f(x)}$ является логарифмически выпуклым, если $f$ является выпуклой функцией. Вместо этого иногда используется термин «сверхвыпуклый».
• Функция $f$ с областью [0,1], определенной формулой $f(0)=f(1)=1,f(x)=0$ для $0<x<1$ является выпуклым; оно непрерывно на открытом интервале $(0,1),$ но не непрерывно при 0 и 1.
• Функция $x^{3}$ имеет вторую производную $6x$; таким образом, он выпуклый на множестве, где $x\geq 0$ и вогнутый на площадке, где $x\leq 0.$
• Примеры функций, которые монотонно возрастают, но не выпуклы, включают: $f(x)={\sqrt {x}}$ и $g(x)=\log x$.
• Примеры функций, которые являются выпуклыми, но не монотонно возрастающими, включают: $h(x)=x^{2}$ и $k(x)=-x$.
• Функция $f(x)={\tfrac {1}{x}}$ имеет $f''(x)={\tfrac {2}{x^{3}}}$ что больше 0, если $x>0$ так $f(x)$ выпукла на отрезке $(0,\infty )$. Оно вогнуто на отрезке $(-\infty ,0)$.
• Функция $f(x)={\tfrac {1}{x^{2}}}$ с $f(0)=\infty$, выпукла на отрезке $(0,\infty )$ и выпуклая на отрезке $(-\infty ,0)$, но не выпуклый на отрезке $(-\infty ,\infty )$, из-за особенности в $x=0.$

Функции n переменных

• Функция LogSumExp , также называемая функцией softmax, является выпуклой функцией.
• Функция $-\log \det(X)$ в области положительно определенных матриц выпукла.
• Всякое вещественнозначное линейное преобразование является выпуклым, но не строго выпуклым, поскольку если $f$ линейно, то $f(a+b)=f(a)+f(b)$. Это утверждение справедливо и в том случае, если мы заменим слово «выпуклое» на «вогнутое».
• Всякая вещественная аффинная функция , то есть каждая функция вида $f(x)=a^{T}x+b,$ одновременно выпуклая и вогнутая.
• Каждая норма является выпуклой функцией в силу неравенства треугольника и положительной однородности .
• Спектральный радиус является неотрицательной матрицы выпуклой функцией ее диагональных элементов.

См. также

• Вогнутая функция
• Выпуклый анализ
• Выпуклое сопряжение
• Выпуклая кривая
• Выпуклая оптимизация
• Геодезическая выпуклость
• Теорема Хана – Банаха
• Неравенство Эрмита–Адамара.
• Функция инвекс
• Неравенство Дженсена
• K-выпуклая функция
• Теорема Качуровского , связывающая выпуклость с монотонностью производной
• Неравенство Караматы
• Логарифмически выпуклая функция
• Псевдовыпуклая функция
• Квазивыпуклая функция
• Субпроизводная выпуклой функции

Ссылки

• Берцекас, Дмитрий (2003). Выпуклый анализ и оптимизация . Афина Сайентифик.
• Борвейн, Джонатан и Льюис, Адриан. (2000). Выпуклый анализ и нелинейная оптимизация. Спрингер.
• Донохью, Уильям Ф. (1969). Распределения и преобразования Фурье . Академическая пресса.
• Хириар-Уррути, Жан-Батист, и Лемарешаль, Клод . (2004). Основы выпуклого анализа. Берлин: Шпрингер.
• Красносельский М.А. , Рутицкий Я.Б. (1961). Выпуклые функции и пространства Орлича . Гронинген: P.Noordhoff Ltd.
• Лауритцен, Нильс (2013). Выпуклость бакалавриата . Мировое научное издательство.
• Люенбергер, Дэвид (1984). Линейное и нелинейное программирование . Аддисон-Уэсли.
• Люенбергер, Дэвид (1969). Оптимизация методами векторного пространства . Уайли и сыновья.
• Рокафеллар, RT (1970). Выпуклый анализ . Принстон: Издательство Принстонского университета.
• Томсон, Брайан (1994). Симметричные свойства действительных функций . ЦРК Пресс.
• Залинеску, К. (2002). Выпуклый анализ в общих векторных пространствах . Ривер Эдж, Нью-Джерси: World Scientific Publishing Co., Inc., стр. xx+367. ISBN  981-238-067-1 . МР   1921556 .

Внешние ссылки

• «Выпуклая функция (действительной переменной)» , Энциклопедия математики , EMS Press , 2001 [1994]
• «Выпуклая функция (комплексной переменной)» , Энциклопедия математики , EMS Press , 2001 [1994]