Изотермический процесс

Изотермический процесс — это тип термодинамического процесса , при котором температура T системы чтобы остается постоянной: Δ T = 0. Обычно это происходит, когда система находится в контакте с внешним тепловым резервуаром , и изменения в системе происходят достаточно медленно, позволяют системе непрерывно подстраиваться под температуру резервуара посредством теплообмена (см. квазиравновесие ). Напротив, адиабатический процесс – это когда система не обменивается теплом с окружающей средой ( Q = 0).

Проще говоря, можно сказать, что в изотермическом процессе

$T={\text{constant}}$
$\Delta T=0$
$dT=0$
для идеальных газов Только внутренняя энергия $\Delta U=0$

а в адиабатических процессах:

$Q=0.$

Этимология

Существительное «изотерма» происходит от древнегреческих слов ἴσος ( isos ), что означает «равный», и θέρμη ( thérmē ), что означает «тепло».

Примеры

Изотермические процессы могут происходить в любой системе, имеющей некоторые средства регулирования температуры, включая высокоструктурированные машины и даже живые клетки. Некоторые части циклов некоторых тепловых двигателей осуществляются изотермически (например, в цикле Карно ). ^[1] При термодинамическом анализе химических реакций обычно сначала анализируют то, что происходит в изотермических условиях, а затем рассматривают влияние температуры. ^[2] Фазовые изменения , такие как плавление или испарение , также являются изотермическими процессами, когда, как это обычно бывает, они происходят при постоянном давлении. ^[3] Изотермические процессы часто используются в качестве отправной точки при анализе более сложных неизотермических процессов.

Изотермические процессы представляют особый интерес для идеальных газов. Это следствие второго закона Джоуля , который гласит, что внутренняя энергия фиксированного количества идеального газа зависит только от его температуры. ^[4] Таким образом, в изотермическом процессе внутренняя энергия идеального газа постоянна. Это результат того, что в идеальном газе нет межмолекулярных сил . ^[4] Обратите внимание, что это верно только для идеальных газов; внутренняя энергия зависит от давления, а также от температуры для жидкостей, твердых тел и реальных газов. ^[5]

При изотермическом сжатии газа в системе совершается работа по уменьшению объема и увеличению давления. ^[4] Совершение работы над газом увеличивает внутреннюю энергию и будет иметь тенденцию к повышению температуры. Для поддержания постоянной температуры энергия должна покинуть систему в виде тепла и попасть в окружающую среду. Если газ идеальный, то количество энергии, поступающей в окружающую среду, равно работе, совершаемой над газом, поскольку внутренняя энергия не меняется. При изотермическом расширении энергия, подаваемая в систему, действует на окружающую среду. В любом случае, с помощью подходящего соединения изменение объема газа может совершить полезную механическую работу. Подробности расчетов см. в разделе Расчет работ .

Для адиабатического процесса , при котором тепло не поступает в газ и не выходит из него, поскольку его контейнер хорошо изолирован, Q = 0. Если также не совершается работа, т. е. происходит свободное расширение , внутренняя энергия не изменяется. Для идеального газа это означает, что процесс также изотермичен. ^[4] Таким образом, указания того, что процесс является изотермическим, недостаточно для определения уникального процесса.

Детали идеального газа

Для частного случая газа, для которого действует закон Бойля ^[4] Если применимо, произведение pV ( p для давления газа и V для объема газа) является константой, если газ содержится в изотермических условиях. Значение константы равно nRT , где n — количество молей текущего газа, а R — постоянная идеального газа . Другими словами, действует закон идеального газа pV = nRT . ^[4] Поэтому:

p={nRT \over V}={{\text{constant}} \over V}

держит. Семейство кривых, порожденных этим уравнением, показано на графике на рисунке 1. Каждая кривая называется изотермой, что означает кривую при одной и той же температуре T . Такие графики называются индикаторными диаграммами и впервые были использованы Джеймсом Уоттом и другими для мониторинга эффективности двигателей. Температура, соответствующая каждой кривой на рисунке, увеличивается слева направо вверх.

Расчет работы

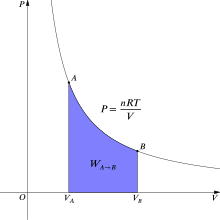
В термодинамике обратимая работа, совершаемая при переходе газа из состояния А в состояние В, равна ^[6]

W_{A\to B}=-\int _{V_{A}}^{V_{B}}p\,dV

где p — давление газа, а V — объем газа. Для изотермического (постоянная температура T ) обратимого процесса этот интеграл равен площади под соответствующей изотермой PV (давление-объем) и для идеального газа обозначен фиолетовым цветом на рисунке 2. Опять же, р = ⁠ nRT / V ⁠ Применяется , и при постоянном значении T (поскольку это изотермический процесс) выражение для работы принимает вид:

W_{A\to B}=-\int _{V_{A}}^{V_{B}}p\,dV=-\int _{V_{A}}^{V_{B}}{\frac {nRT}{V}}dV=-nRT\int _{V_{A}}^{V_{B}}{\frac {1}{V}}dV=-nRT\ln {\frac {V_{B}}{V_{A}}}

В конвенции ИЮПАК работа определяется как работа над системой в ее окружении. Если, например, система сжимается, то работа над системой совершается окружающей средой, поэтому работа положительна, а внутренняя энергия системы увеличивается. И наоборот, если система расширяется (т. е. расширяется вокруг системы, поэтому свободное расширение не имеет места), то работа отрицательна, поскольку система совершает работу с окружающей средой, и внутренняя энергия системы уменьшается.

Также стоит отметить, что для идеальных газов, если температура поддерживается постоянной, внутренняя энергия системы U также постоянна, и поэтому Δ U = 0. Поскольку Первый закон термодинамики гласит, что Δ U = Q + W в Согласно соглашению ИЮПАК , из этого следует, что Q = − W для изотермического сжатия или расширения идеальных газов.

Пример изотермического процесса

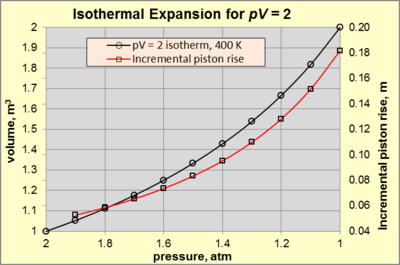
Обратимое расширение идеального газа можно использовать как пример работы, совершаемой в результате изотермического процесса. Особый интерес представляет степень, в которой тепло преобразуется в полезную работу, а также взаимосвязь между удерживающей силой и степенью расширения.

Во время изотермического расширения идеального газа и $p$ , и $V$ изменяются вдоль изотермы с постоянным $произведением pV$ (т. е. постоянным T ). Рассмотрим рабочий газ в цилиндрической камере высотой 1 м и высотой 1 м. ² площадь (так 1м ³ объём) при 400 К в статическом равновесии . Окружающая среда состоит из воздуха с температурой 300 К и давлением 1 атм (обозначается $p surr$ ). Рабочий газ удерживается поршнем, соединенным с механическим устройством, оказывающим силу, достаточную для создания давления рабочего газа 2 атм (состояние $А$ ). При любом изменении состояния $А$ , вызывающем уменьшение силы, газ будет расширяться и совершать работу с окружающей средой. Изотермическое расширение продолжается до тех пор, пока приложенная сила уменьшается и добавляется соответствующее тепло, чтобы поддерживать $pV$ = 2 [атм·м ³] (= 2 атм × 1 м ³). Расширение называется внутренне обратимым, если движение поршня достаточно медленное, так что в каждый момент расширения температура и давление газа однородны и соответствуют закону идеального газа . На рис. 3 показана $зависимость p - V$ для $pV$ = 2 [атм·м ³] для изотермического расширения от 2 атм (состояние $А$ ) до 1 атм (состояние $Б$ ).

Выполненная работа (обозначена $W_{A\to B}$ ) состоит из двух компонентов. Во-первых, это работа расширения против давления окружающей атмосферы (обозначается как $W p Δ V$ ), а во-вторых, полезная механическая работа (обозначается как $W mech$ ). Выходным $W механизмом$ здесь может быть движение поршня, используемого для поворота кривошипа, который затем поворачивает шкив, способный поднимать воду из затопленных соляных шахт .

W_{A\to B}=-p\,V\left(\ln {\frac {V_{B}}{V_{A}}}\right)=-W_{p\Delta V}-W_{\rm {mech}}

Система достигает состояния $B$ ( $pV$ = 2 [атм·м ³] с $p$ = 1 атм и $V$ = 2 м ³), когда приложенная сила достигает нуля. В этот момент $W_{A\to B}$ равен –140,5 кДж, а $W p Δ V$ – –101,3 кДж. По разнице $W мех$ = –39,1 кДж, что составляет 27,9% от тепла, подаваемого в процесс (- 39,1 кДж / – 140,5 кДж). Это максимальное количество полезной механической работы, которую можно получить в результате процесса при указанных условиях. Процент $W mech$ является функцией $pV$ и $p surr$ и приближается к 100%, когда $p surr$ приближается к нулю.

Чтобы понять природу изотермического расширения, обратите внимание на красную линию на рисунке 3. Фиксированное значение $pV$ вызывает экспоненциальное увеличение подъема поршня по сравнению с уменьшением давления. Например, снижение давления с 2 до 1,9 атм вызывает подъем поршня на 0,0526 м. Для сравнения, снижение давления с 1,1 до 1 атм вызывает подъем поршня на 0,1818 м.

Изменения энтропии

Изотермические процессы особенно удобны для расчета изменения энтропии , поскольку в этом случае формула изменения энтропии Δ S имеет простой вид:

\Delta S={\frac {Q_{\text{rev}}}{T}}

где Q _rev — тепло, передаваемое (внутренне обратимое) системе, а T — абсолютная температура . ^[7] Эта формула справедлива только для гипотетического обратимого процесса ; то есть процесс, в котором равновесие поддерживается все время.

Простым примером является равновесный фазовый переход (такой как плавление или испарение), происходящий при постоянной температуре и давлении. При фазовом переходе при постоянном давлении переданное системе тепло равно энтальпии превращения Δ H _tr , таким образом Q = Δ H _tr . ^[3] При любом заданном давлении будет температура перехода T _tr , при которой две фазы находятся в равновесии (например, нормальная температура кипения жидкости при давлении в одну атмосферу). Если переход происходит в таких условиях равновесия, приведенную выше формулу можно использовать для непосредственного расчета изменения энтропии. ^[7]

\Delta S_{\text{tr}}={\frac {\Delta H_{\text{tr}}}{T_{\text{tr}}}}

.

Другим примером является обратимое изотермическое расширение (или сжатие) идеального газа от начального объема V _A и давления P _A до конечного объема V _B и давления P _B . Как показано в расчете работы , теплота, переданная газу, равна

Q=-W=nRT\ln {\frac {V_{\text{B}}}{V_{\text{A}}}}

.

Этот результат относится к обратимому процессу, поэтому его можно подставить в формулу изменения энтропии, чтобы получить ^[7]

\Delta S=nR\ln {\frac {V_{\text{B}}}{V_{\text{A}}}}

.

Поскольку идеальный газ подчиняется закону Бойля , его при желании можно переписать в виде

\Delta S=nR\ln {\frac {P_{\text{A}}}{P_{\text{B}}}}

.

После получения эти формулы можно применить к необратимому процессу , например к свободному расширению идеального газа. Такое расширение также является изотермическим и может иметь те же начальное и конечное состояния, что и при обратимом расширении. Поскольку энтропия является функцией состояния (зависящей от состояния равновесия, а не от пути, по которому система достигает этого состояния), изменение энтропии системы такое же, как и в обратимом процессе, и определяется формулами выше. Обратите внимание, что результат Q = 0 для свободного расширения не может быть использован в формуле изменения энтропии, поскольку процесс необратим.

Разница между обратимым и необратимым заключается в энтропии окружающей среды. В обоих случаях окружающая среда имеет постоянную температуру T , так что Δ S _sur = − ⁠ К / Т ⁠ ; знак минус используется, поскольку тепло, передаваемое в окружающую среду, равно по величине и противоположно по знаку теплу Q , передаваемому системе. В обратимом случае изменение энтропии окружающей среды равно и противоположно изменению системы, поэтому изменение энтропии Вселенной равно нулю. В необратимом случае Q = 0, поэтому энтропия окружающей среды не меняется и изменение энтропии Вселенной равно ΔS для системы.

См. также

Ссылки

^ Кинан, Дж. Х. (1970). «Глава 12: Циклы тепловых двигателей». Термодинамика . Кембридж, Массачусетс: MIT Press.
^ Рок, Пенсильвания (1983). «Глава 11: Термодинамика химических реакций». Химическая термодинамика . Милл-Вэлли, Калифорния: Университетские научные книги. ISBN 0-935702-12-1 .
^ Jump up to: ^а ^б Петруччи, Р.Х.; Харвуд, Вашингтон; Херринг, ФГ; Мадура, JD (2007). «Глава 12». Общая химия . Река Аппер-Седл, Нью-Джерси: Пирсон. ISBN 978-0-13-149330-8 .
^ Jump up to: ^а ^б ^с ^д ^и ^ж Клотц, И.М.; Розенберг, Р.М. (1991). «Глава 6. Применение первого закона к газам». Химическая термодинамика . Мено-Парк, Калифорния: Бенджамин. ^{[ ISBN отсутствует ]}
^ Адкинс, CJ (1983). Равновесная термодинамика . Кембридж: Издательство Кембриджского университета. ^{[ ISBN отсутствует ]}
^ Аткинс, Питер (1997). «Глава 2: Первый закон: понятия». Физическая химия (6-е изд.). Нью-Йорк, штат Нью-Йорк: ISBN WH Freeman and Co. 0-7167-2871-0 .
^ Jump up to: ^а ^б ^с Аткинс, Питер (1997). «Глава 4: Второй закон: понятия». Физическая химия (6-е изд.). Нью-Йорк, штат Нью-Йорк: ISBN WH Freeman and Co. 0-7167-2871-0 .

[1] Кинан, Дж. Х. (1970). «Глава 12: Циклы тепловых двигателей». Термодинамика . Кембридж, Массачусетс: MIT Press.

[:Rock-2] Рок, Пенсильвания (1983). «Глава 11: Термодинамика химических реакций». Химическая термодинамика . Милл-Вэлли, Калифорния: Университетские научные книги. ISBN 0-935702-12-1 .

[Petrucci-3] Jump up to: ^а ^б Петруччи, Р.Х.; Харвуд, Вашингтон; Херринг, ФГ; Мадура, JD (2007). «Глава 12». Общая химия . Река Аппер-Седл, Нью-Джерси: Пирсон. ISBN 978-0-13-149330-8 .

[Klotz-4] Jump up to: ^а ^б ^с ^д ^и ^ж Клотц, И.М.; Розенберг, Р.М. (1991). «Глава 6. Применение первого закона к газам». Химическая термодинамика . Мено-Парк, Калифорния: Бенджамин. ^{[ ISBN отсутствует ]}

[5] Адкинс, CJ (1983). Равновесная термодинамика . Кембридж: Издательство Кембриджского университета. ^{[ ISBN отсутствует ]}

[:Atkins-6] Аткинс, Питер (1997). «Глава 2: Первый закон: понятия». Физическая химия (6-е изд.). Нью-Йорк, штат Нью-Йорк: ISBN WH Freeman and Co. 0-7167-2871-0 .

[Atkins4-7] Jump up to: ^а ^б ^с Аткинс, Питер (1997). «Глава 4: Второй закон: понятия». Физическая химия (6-е изд.). Нью-Йорк, штат Нью-Йорк: ISBN WH Freeman and Co. 0-7167-2871-0 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]