Уравнение непрерывности

Уравнение непрерывности или уравнение переноса — это уравнение , описывающее перенос некоторой величины. Он особенно прост и эффективен, когда применяется к сохраняющейся величине , но его можно обобщить и применить к любому экстенсивному количеству . Поскольку масса , энергия , импульс , электрический заряд и другие естественные величины сохраняются при соответствующих условиях, множество физических явлений можно описать с помощью уравнений непрерывности.

Уравнения непрерывности представляют собой более сильную локальную форму законов сохранения . Например, слабая версия закона сохранения энергии гласит, что энергия не может быть ни создана, ни уничтожена, т. е. общее количество энергии во Вселенной фиксировано. Это утверждение не исключает возможности того, что определенное количество энергии может исчезнуть из одной точки и одновременно появиться в другой точке. Более сильное утверждение состоит в том, что энергия локально сохраняется: энергия не может быть ни создана, ни уничтожена, и она не может « телепортироваться » из одного места в другое — она может перемещаться только непрерывным потоком. Уравнение непрерывности — это математический способ выражения такого рода утверждений. Например, уравнение непрерывности электрического заряда гласит, что количество электрического заряда в любом объеме пространства может меняться только в зависимости от количества электрического тока, втекающего в этот объем или выходящего из него через его границы.

Уравнения непрерывности в более общем смысле могут включать термины «источник» и «приемник», которые позволяют им описывать величины, которые часто, но не всегда, сохраняются, например, плотность молекулярных частиц, которые могут создаваться или разрушаться в результате химических реакций. В повседневном примере существует уравнение непрерывности для количества живущих людей; у него есть «исходный термин», учитывающий рождение людей, и «поглощающий термин», учитывающий смерть людей.

Любое уравнение неразрывности может быть выражено в «интегральной форме» (в терминах интеграла потока ), которая применима к любой конечной области, или в «дифференциальной форме» (в терминах оператора дивергенции ), которая применяется в точке.

Уравнения непрерывности лежат в основе более конкретных уравнений переноса, таких как уравнение конвекции-диффузии , уравнение переноса Больцмана и уравнения Навье-Стокса .

Потоки, определяемые уравнениями неразрывности, можно визуализировать с помощью диаграммы Сэнки .

Общее уравнение

Определение потока

Уравнение непрерывности полезно, когда поток можно определить . Чтобы определить поток, сначала должна быть величина $q,$ которая может течь или двигаться, например масса , энергия , электрический заряд , импульс , число молекул и т. д. Пусть $ρ$ — объемная плотность этой величины, то есть количество $q$ на единицу объема.

То, как течет это количество $q,$ описывается его потоком. Поток $q$ представляет собой векторное поле , которое мы обозначаем как j . Вот несколько примеров и свойств флюса:

Размерность потока - это «количество $q$ , протекающее в единицу времени через единицу площади». Например, в уравнении неразрывности текущей воды, если по трубе с площадью поперечного сечения 1 см протекает 1 грамм воды в секунду. ², то средний поток массы $j$ внутри трубы равен (1 г/с)/см ², а его направление — вдоль трубы по направлению течения воды. Вне трубы, где нет воды, поток равен нулю.
Если существует поле скорости $u$ , которое описывает соответствующий поток — другими словами, если вся величина $q$ в точке $x$ движется со скоростью $u (x)$ — тогда поток по определению равен плотности, умноженной на поле скорости. :

\mathbf {j} =\rho \mathbf {u}

Например, если в уравнении непрерывности массы текущей воды

u

— скорость воды в каждой точке, а

ρ

— плотность воды в каждой точке, то

j

будет потоком массы, также известным как расход материала .

В известном примере поток электрического заряда — это плотность электрического тока .

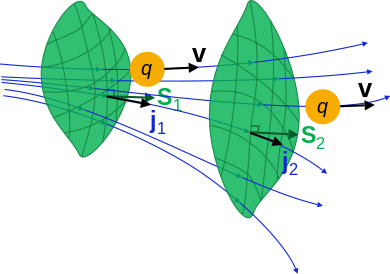
Если существует воображаемая поверхность $S$ , то поверхностный интеграл потока по $S$ равен количеству $q$ , которое проходит через поверхность $S$ в единицу времени:

$({\text{Rate that }}q{\text{ is flowing through the imaginary surface }}S)=\iint _{S}\mathbf {j} \cdot d\mathbf {S}$

в котором

{\textstyle \iint _{S}d\mathbf {S} }

является поверхностным интегралом .

(Обратите внимание, что понятие, которое здесь называется «поток», в некоторой литературе альтернативно называется плотностью потока , в этом контексте «поток» обозначает поверхностный интеграл плотности потока. см. В основной статье о потоке Подробности .)

Интегральная форма

Интегральная форма уравнения непрерывности гласит, что:

Количество $q$ в области увеличивается, когда дополнительный $q$ течет внутрь через поверхность области, и уменьшается, когда он течет наружу;
Количество $q$ в регионе увеличивается, когда $новый q$ внутри региона создается $, и уменьшается, когда q$ уничтожается;
Помимо этих двух процессов, нет другого способа изменить количество $q$ в области.

Математически интегральная форма уравнения непрерывности, выражающая скорость увеличения $q$ в объеме $V,$ равна:

${\frac {dq}{dt}}+\oint _{S}\mathbf {j} \cdot d\mathbf {S} =\Sigma$

В интегральной форме уравнения непрерывности $S$ — это любая замкнутая поверхность , полностью охватывающая объем $V$ , как и любая из поверхностей слева. $S$ может не быть поверхностью с границами, как показано справа. (Поверхности синие, границы красные.)

где

$S$ — любая воображаемая замкнутая поверхность , заключающая в себе объем $V$ ,
$\oint _{S}d\mathbf {S}$ обозначает поверхностный интеграл по этой замкнутой поверхности,
$q$ — общий объем количества в объеме $V$ ,
$j$ — поток $q$ ,
$это$ время,
$Σ$ — чистая скорость, с которой $q$ генерируется внутри объема $V$ в единицу времени. Когда $q$ генерируется, его называют q , $Σ$ и это делает $источником$ более положительным. Когда $q$ разрушается, это называется q , $Σ$ и это делает $стоком$ более отрицательным. Иногда этот термин пишут как $dq/dt|_{\text{gen}}$ или полное изменение q в результате его образования или разрушения внутри контрольного объема.

В простом примере $V$ может быть зданием, а $q$ — количеством людей в здании. Поверхность $S$ будет состоять из стен, дверей, крыши и фундамента здания. Тогда уравнение непрерывности утверждает, что количество людей в здании увеличивается, когда люди входят в здание (внутренний поток через поверхность), уменьшается, когда люди выходят из здания (исходящий поток через поверхность), увеличивается, когда кто-то в здании дает рождения (источник, $Σ > 0$ ) и уменьшается, когда кто-то в здании умирает (приемник, $Σ < 0$ ).

Дифференциальная форма

По теореме о дивергенции общее уравнение неразрывности можно записать и в «дифференциальной форме»:

${\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {j} =\sigma$

где

$\nabla\cdot$ — дивергенция ,
$ρ$ — плотность количества $q$ (т.е. количества $q$ на единицу объема),
$j$ — плотность потока $q$ (т.е. j = ρ v , где v — векторное поле, описывающее движение величины $q$ ),
$это$ время,
$σ$ — генерирование $q$ на единицу объема в единицу времени. Термы, которые генерируют $q$ (т. е. $σ > 0$ ) или удаляют $q$ (т. е. $σ < 0$ ), называются «источниками» и «приемниками» соответственно.

Это общее уравнение можно использовать для вывода любого уравнения неразрывности, от такого простого, как уравнение неразрывности объема, до столь сложного, как уравнения Навье – Стокса . Это уравнение также обобщает уравнение переноса . Другие уравнения в физике, такие как закон Гаусса для электрического поля и закон Гаусса для гравитации , имеют математическую форму, аналогичную уравнению неразрывности, но обычно не называются термином «уравнение непрерывности», потому что $j$ в этих случаях не представляют собой поток реальной физической величины.

В случае, когда $q$ является сохраняющейся величиной , которую нельзя создать или уничтожить (например, энергия ), $σ = 0$ , и уравнения принимают вид: ${\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {j} =0$

Электромагнетизм

В теории электромагнетизма уравнение неразрывности представляет собой эмпирический закон, выражающий (локальное) сохранение заряда . Математически это является автоматическим следствием уравнений Максвелла , хотя сохранение заряда является более фундаментальным, чем уравнения Максвелла. В нем говорится, что дивергенция плотности тока $J$ (в амперах на квадратный метр) равна отрицательной скорости изменения плотности заряда $ρ$ (в кулонах на кубический метр), $\nabla \cdot \mathbf {J} =-{\frac {\partial \rho }{\partial t}}$

Согласованность с уравнениями Максвелла

Одно из уравнений Максвелла , закон Ампера (с поправкой Максвелла) , гласит, что $\nabla \times \mathbf {H} =\mathbf {J} +{\frac {\partial \mathbf {D} }{\partial t}}.$

Если принять расхождение обеих сторон (расхождение и частную производную при коммутации по времени), то получим $\nabla \cdot (\nabla \times \mathbf {H} )=\nabla \cdot \mathbf {J} +{\frac {\partial (\nabla \cdot \mathbf {D} )}{\partial t}},$ но расходимость ротора равна нулю, так что $\nabla \cdot \mathbf {J} +{\frac {\partial (\nabla \cdot \mathbf {D} )}{\partial t}}=0.$

Но закон Гаусса (еще одно уравнение Максвелла) гласит, что $\nabla \cdot \mathbf {D} =\rho ,$ которое можно подставить в предыдущее уравнение, чтобы получить уравнение неразрывности $\nabla \cdot \mathbf {J} +{\frac {\partial \rho }{\partial t}}=0.$

Ток – это движение заряда. Уравнение непрерывности гласит, что если заряд выходит из дифференциального объема (т. е. дивергенция плотности тока положительна), то количество заряда внутри этого объема будет уменьшаться, поэтому скорость изменения плотности заряда отрицательна. Следовательно, уравнение непрерывности сводится к сохранению заряда.

Если бы магнитные монополи существовали, то существовало бы и уравнение непрерывности для монопольных токов; предысторию и двойственность между электрическим и магнитным токами см. в статье о монополях.

Гидродинамика

В гидродинамике уравнение непрерывности гласит, что скорость, с которой масса входит в систему, равна скорости, с которой масса покидает систему, плюс накопление массы внутри системы. ^{[ 1 ]}^{[ 2 ]} Дифференциальная форма уравнения неразрывности имеет вид: ^{[ 1 ]} ${\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho \mathbf {u} )=0$ где

$ρ$ жидкости — плотность ,
$это$ время,
$u$ — скорости потока векторное поле .

Производную по времени можно понимать как накопление (или потерю) массы в системе, тогда как член дивергенции представляет собой разницу притока и оттока. В этом контексте это уравнение также является одним из уравнений Эйлера (гидродинамики) . Уравнения Навье – Стокса образуют векторное уравнение неразрывности, описывающее сохранение линейного импульса .

Если жидкость несжимаема (объемная скорость деформации равна нулю), уравнение неразрывности массы упрощается до уравнения неразрывности объема: ^{[ 3 ]} $\nabla \cdot \mathbf {u} =0,$ а это означает, что дивергенция поля скорости всюду равна нулю. Физически это эквивалентно утверждению, что локальная скорость расширения объема равна нулю, следовательно, поток воды через сужающуюся трубу будет корректироваться исключительно за счет увеличения его скорости, поскольку вода в значительной степени несжимаема.

Компьютерное зрение

В компьютерном зрении оптический поток — это закономерность видимого движения объектов в визуальной сцене. Предполагая, что яркость движущегося объекта не изменилась между двумя кадрами изображения, можно вывести уравнение оптического потока как: ^{[ нужна ссылка ]} ${\frac {\partial I}{\partial x}}V_{x}+{\frac {\partial I}{\partial y}}V_{y}+{\frac {\partial I}{\partial t}}=\nabla I\cdot \mathbf {V} +{\frac {\partial I}{\partial t}}=0$ где

$это$ время,
$координаты x, y$ на изображении,
$I$ — интенсивность изображения в координате изображения $(x, y)$ и времени $t$ ,
$V$ — вектор скорости оптического потока. $(V_{x},V_{y})$ в координате изображения $(x, y)$ и времени $t$

Энергия и тепло

Сохранение энергии говорит о том, что энергию невозможно создать или уничтожить. ( см. ниже Нюансы, связанные с общей теорией относительности, .) Следовательно, существует уравнение непрерывности потока энергии: ${\frac {\partial u}{\partial t}}+\nabla \cdot \mathbf {q} =0$ где

$u$ , локальная плотность энергии (энергия на единицу объема),
$q$ , поток энергии (перенос энергии на единицу площади поперечного сечения в единицу времени) в виде вектора,

Важным практическим примером является поток тепла . Когда тепло течет внутри твердого тела, уравнение неразрывности можно объединить с законом Фурье (тепловой поток пропорционален градиенту температуры), чтобы получить уравнение теплопроводности . Уравнение теплового потока также может иметь исходные члены: хотя энергия не может быть создана или уничтожена, тепло может быть создано из других видов энергии, например, посредством трения или джоулевого нагрева .

Распределения вероятностей

Если существует величина, которая движется непрерывно в соответствии со стохастическим (случайным) процессом, например, положение одной растворенной молекулы с броуновским движением , то существует уравнение непрерывности для ее распределения вероятностей . Поток в данном случае — это вероятность прохождения частицы через поверхность на единицу площади в единицу времени. Согласно уравнению неразрывности, отрицательная дивергенция этого потока равна скорости изменения плотности вероятности . Уравнение непрерывности отражает тот факт, что молекула всегда где-то находится (интеграл от ее распределения вероятностей всегда равен 1) и что она движется непрерывным движением (без телепортации ).

Квантовая механика

Квантовая механика — еще одна область, в которой существует уравнение непрерывности, связанное с сохранением вероятности . Термины в уравнении требуют следующих определений и немного менее очевидны, чем другие примеры выше, поэтому они изложены здесь:

Ψ Волновая функция $для$ отдельной частицы в пространстве позиций (а не в пространстве импульсов ), то есть функция положения $r$ и времени $t$ , $Ψ = Ψ(r, t)$ .
Функция плотности вероятности $\rho (\mathbf {r} ,t)=\Psi ^{*}(\mathbf {r} ,t)\Psi (\mathbf {r} ,t)=|\Psi (\mathbf {r} ,t)|^{2}.$
Вероятность как обнаружения частицы внутри $V$ в момент $t$ обозначается и определяется $P=P_{\mathbf {r} \in V}(t)=\int _{V}\Psi ^{*}\Psi dV=\int _{V}|\Psi |^{2}dV.$
Вероятностный ток (поток вероятности) равен $\mathbf {j} (\mathbf {r} ,t)={\frac {\hbar }{2mi}}\left[\Psi ^{*}\left(\nabla \Psi \right)-\Psi \left(\nabla \Psi ^{*}\right)\right].$

С этими определениями уравнение непрерывности выглядит следующим образом: $\nabla \cdot \mathbf {j} +{\frac {\partial \rho }{\partial t}}=0\mathrel {\rightleftharpoons } \nabla \cdot \mathbf {j} +{\frac {\partial |\Psi |^{2}}{\partial t}}=0.$

Любая форма может быть цитирована. Интуитивно понятно, что приведенные выше величины указывают на то, что это представляет собой поток вероятностей. Шанс ; найти частицу в некоторой позиции $r$ и времени $t$ как жидкость течет отсюда термин «вероятностный ток» — векторное поле . Сама частица не течет детерминированно в этом векторном поле .

Согласованность с уравнением Шредингера

Зависящее от времени уравнение Шредингера и его комплексно-сопряженное уравнение ( $i \to - i$ повсюду) имеют вид соответственно: ^{[ 4 ]} ${\begin{aligned}-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi +U\Psi &=i\hbar {\frac {\partial \Psi }{\partial t}},\\-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi ^{*}+U\Psi ^{*}&=-i\hbar {\frac {\partial \Psi ^{*}}{\partial t}},\\\end{aligned}}$ где $U$ — потенциальная функция . Частная производная ρ $$ по $t$ : ${\frac {\partial \rho }{\partial t}}={\frac {\partial |\Psi |^{2}}{\partial t}}={\frac {\partial }{\partial t}}\left(\Psi ^{*}\Psi \right)=\Psi ^{*}{\frac {\partial \Psi }{\partial t}}+\Psi {\frac {\partial \Psi ^{*}}{\partial t}}.$

Умножив уравнение Шрёдингера на $Ψ*,$ затем найдя $Ψ* .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ ∂Ψ / ∂ t ⁠$ и аналогичным образом умножив комплексное сопряженное уравнение Шредингера на $Ψ,$ затем найдя $Ψ ⁠ \partialΨ* / \partial t ⁠$ ; ${\begin{aligned}\Psi ^{*}{\frac {\partial \Psi }{\partial t}}&={\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi ^{*}}{2m}}\nabla ^{2}\Psi +U\Psi ^{*}\Psi \right],\\\Psi {\frac {\partial \Psi ^{*}}{\partial t}}&=-{\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi }{2m}}\nabla ^{2}\Psi ^{*}+U\Psi \Psi ^{*}\right],\\\end{aligned}}$

подставив в производную по времени $ρ$ : ${\begin{aligned}{\frac {\partial \rho }{\partial t}}&={\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi ^{*}}{2m}}\nabla ^{2}\Psi +U\Psi ^{*}\Psi \right]-{\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi }{2m}}\nabla ^{2}\Psi ^{*}+U\Psi \Psi ^{*}\right]\\&={\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi ^{*}}{2m}}\nabla ^{2}\Psi +U\Psi ^{*}\Psi \right]+{\frac {1}{i\hbar }}\left[+{\frac {\hbar ^{2}\Psi }{2m}}\nabla ^{2}\Psi ^{*}-U\Psi ^{*}\Psi \right]\\[2pt]&=-{\frac {1}{i\hbar }}{\frac {\hbar ^{2}\Psi ^{*}}{2m}}\nabla ^{2}\Psi +{\frac {1}{i\hbar }}{\frac {\hbar ^{2}\Psi }{2m}}\nabla ^{2}\Psi ^{*}\\[2pt]&={\frac {\hbar }{2im}}\left[\Psi \nabla ^{2}\Psi ^{*}-\Psi ^{*}\nabla ^{2}\Psi \right]\\\end{aligned}}$

Операторы Лапласа ( $\nabla 2$ ) в приведенном выше результате предполагают, что правая часть представляет собой расхождение $j$ , а обратный порядок членов подразумевает, что это в целом отрицательное значение $j$ : ${\begin{aligned}\nabla \cdot \mathbf {j} &=\nabla \cdot \left[{\frac {\hbar }{2mi}}\left(\Psi ^{*}\left(\nabla \Psi \right)-\Psi \left(\nabla \Psi ^{*}\right)\right)\right]\\&={\frac {\hbar }{2mi}}\left[\Psi ^{*}\left(\nabla ^{2}\Psi \right)-\Psi \left(\nabla ^{2}\Psi ^{*}\right)\right]\\&=-{\frac {\hbar }{2mi}}\left[\Psi \left(\nabla ^{2}\Psi ^{*}\right)-\Psi ^{*}\left(\nabla ^{2}\Psi \right)\right]\\\end{aligned}}$ поэтому уравнение непрерывности имеет вид: ${\begin{aligned}&{\frac {\partial \rho }{\partial t}}=-\nabla \cdot \mathbf {j} \\[3pt]{}\Rightarrow {}&{\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {j} =0\\\end{aligned}}$

Интегральная форма следующая, как и для общего уравнения.

Полупроводник

Общий ток в полупроводнике состоит из дрейфового тока и диффузионного тока как электронов в зоне проводимости, так и дырок в валентной зоне.

Общая форма для одномерных электронов: ${\frac {\partial n}{\partial t}}=n\mu _{n}{\frac {\partial E}{\partial x}}+\mu _{n}E{\frac {\partial n}{\partial x}}+D_{n}{\frac {\partial ^{2}n}{\partial x^{2}}}+(G_{n}-R_{n})$ где:

n - локальная концентрация электронов
$\mu _{n}$ подвижность электронов
E - электрическое поле в области обеднения.
D _n – коэффициент диффузии электронов
G _n – скорость генерации электронов
R _n – скорость рекомбинации электронов

Аналогично для дырок: ${\frac {\partial p}{\partial t}}=-p\mu _{p}{\frac {\partial E}{\partial x}}-\mu _{p}E{\frac {\partial p}{\partial x}}+D_{p}{\frac {\partial ^{2}p}{\partial x^{2}}}+(G_{p}-R_{p})$ где:

p — локальная концентрация дырок
$\mu _{p}$ подвижность дырок
E - электрическое поле в области обеднения.
D _p — коэффициент диффузии дырок
G _p — скорость образования дырок
R _p – скорость рекомбинации дырок

Вывод

В этом разделе представлен вывод приведенного выше уравнения для электронов. Аналогичный вывод можно найти и для уравнения для дырок.

Учтите тот факт, что количество электронов сохраняется в объеме полупроводникового материала с площадью поперечного сечения A и длиной dx вдоль оси x . Точнее можно сказать: ${\text{Rate of change of electron density}}=({\text{Electron flux in}}-{\text{Electron flux out}})+{\text{Net generation inside a volume}}$

Математически это равенство можно записать: ${\begin{aligned}{\frac {dn}{dt}}A\,dx&=\left[J(x+dx)-J(x)\right]{\frac {A}{e}}+(G_{n}-R_{n})A\,dx\\&=\left[J(x)+{\frac {dJ}{dx}}dx-J(x)\right]{\frac {A}{e}}+(G_{n}-R_{n})A\,dx\\[1.2ex]{\frac {dn}{dt}}&={\frac {1}{e}}{\frac {dJ}{dx}}+(G_{n}-R_{n})\end{aligned}}$ Здесь J обозначает плотность тока (направление которого условно направлено против потока электронов), обусловленного потоком электронов внутри рассматриваемого объема полупроводника. Ее еще называют плотностью электронного тока.

Полная плотность электронного тока представляет собой сумму плотностей дрейфового и диффузионного тока: $J_{n}=en\mu _{n}E+eD_{n}{\frac {dn}{dx}}$

Поэтому у нас есть ${\frac {dn}{dt}}={\frac {1}{e}}{\frac {d}{dx}}\left(en\mu _{n}E+eD_{n}{\frac {dn}{dx}}\right)+(G_{n}-R_{n})$

Применение правила произведения приводит к окончательному выражению: ${\frac {dn}{dt}}=\mu _{n}E{\frac {dn}{dx}}+\mu _{n}n{\frac {dE}{dx}}+D_{n}{\frac {d^{2}n}{dx^{2}}}+(G_{n}-R_{n})$

Решение

Ключом к решению этих уравнений в реальных устройствах является, когда это возможно, выбор областей, в которых большинство механизмов пренебрежимо малы, чтобы уравнения сводились к гораздо более простой форме.

Релятивистская версия

Специальная теория относительности

Обозначения и инструменты специальной теории относительности , особенно 4-вектора и 4-градиента , предлагают удобный способ написать любое уравнение непрерывности.

Плотность величины $ρ$ и ее ток $j$ можно объединить в 4-вектор, называемый 4-током : $J=\left(c\rho ,j_{x},j_{y},j_{z}\right)$ где $с$ — скорость света . 4- дивергенция этого тока равна: $\partial _{\mu }J^{\mu }=c{\frac {\partial \rho }{\partial ct}}+\nabla \cdot \mathbf {j}$ где $\partial µ$ — 4-градиент , а $µ$ — индекс, обозначающий пространства-времени измерение . Тогда уравнение неразрывности имеет вид: $\partial _{\mu }J^{\mu }=0$ в обычном случае, когда нет ни источников, ни стоков, то есть для идеально сохраняющихся величин, таких как энергия или заряд. Это уравнение неразрывности явно («очевидно») лоренц-инвариантно .

Примеры уравнений непрерывности, часто записываемых в такой форме, включают сохранение электрического заряда. $\partial _{\mu }J^{\mu }=0$ где $J$ — электрический 4-ток ; и сохранение энергии-импульса $\partial _{\nu }T^{\mu \nu }=0$ где $T$ – тензор энергии-импульса .

Общая теория относительности

В общей теории относительности , где пространство-время искривлено, уравнение непрерывности (в дифференциальной форме) для энергии, заряда или других сохраняющихся величин включает в себя ковариантную дивергенцию вместо обычной дивергенции.

Например, тензор энергии-импульса второго порядка представляет собой тензорное поле , содержащее плотности энергии-импульса, потоки энергии-импульса и касательные напряжения распределения массы-энергии. Дифференциальная форма сохранения энергии-импульса в общей теории относительности утверждает, что ковариантная дивергенция тензора энергии-импульса равна нулю: ${T^{\mu }}_{\nu ;\mu }=0.$

Это важное ограничение на форму, которую принимают уравнения поля Эйнштейна в общей теории относительности . ^{[ 5 ]}

Однако обычная расходимость тензора энергии-импульса не обязательно исчезает: ^{[ 6 ]} $\partial _{\mu }T^{\mu \nu }=-\Gamma _{\mu \lambda }^{\mu }T^{\lambda \nu }-\Gamma _{\mu \lambda }^{\nu }T^{\mu \lambda },$

Правая часть строго обращается в нуль только для плоской геометрии.

Как следствие, интегральную форму уравнения неразрывности трудно определить, и она не обязательно справедлива для области, в которой пространство-время существенно искривлено (например, вокруг черной дыры или по всей Вселенной). ^{[ 7 ]}

Физика элементарных частиц

Кварки и глюоны имеют цветовой заряд , который всегда сохраняется как электрический заряд, и для таких токов цветного заряда существует уравнение непрерывности (явные выражения для токов даются в тензоре напряженности поля глюонов ).

В физике элементарных частиц есть много других величин, которые часто или всегда сохраняются: барионное число (пропорциональное числу кварков минус число антикварков), число электронов, мю-число, тау-число , изоспин и другие. ^{[ 8 ]} Каждому из них соответствует уравнение непрерывности, возможно, включающее условия источника/приемника.

Теорема Нётер

Одной из причин того, что уравнения сохранения часто встречаются в физике, является теорема Нётер . Это означает, что всякий раз, когда законы физики обладают непрерывной симметрией , существует уравнение непрерывности для некоторой сохраняющейся физической величины. Три наиболее известных примера:

Законы физики инвариантны относительно перевода времени — например, законы физики сегодня такие же, как и вчера. Эта симметрия приводит к уравнению непрерывности сохранения энергии .
Законы физики инвариантны относительно перемещения в пространстве — например, ракета в космическом пространстве не подвергается воздействию различных сил или потенциалов, если она смещается в любом заданном направлении (например, x, y, z), что приводит к сохранение трех компонентов импульса сохранение импульса .
Законы физики инвариантны относительно ориентации — например, плавая в космическом пространстве, невозможно измерить, чтобы сказать: «Какая сторона вверху»; законы физики одни и те же, независимо от того, как вы ориентируетесь. Эта симметрия приводит к уравнению неразрывности сохранения углового момента .

См. также

Ссылки

^ Перейти обратно: ^а ^б Педлоски, Джозеф (1987). Геофизическая гидродинамика . Спрингер . стр. 10–13 . ISBN 978-0-387-96387-7 .
^ Клэнси, LJ (1975), Аэродинамика , Раздел 3.3, Pitman Publishing Limited, Лондон
^ Филдинг, Сюзанна. «Основы гидродинамики» (PDF) . Даремский университет . Проверено 22 декабря 2019 г.
^ Об этом выводе см., например. МакМахон, Д. (2006). Квантовая механика демистифицирована . МакГроу Хилл. ISBN 0-07-145546-9 .
^ Д. МакМахон (2006). Демистифицированная теория относительности . МакГроу Хилл (США). ISBN 0-07-145545-0 .
^ К.В. Миснер; К.С. Торн; Дж. А. Уилер (1973). Гравитация . WH Freeman & Co. ISBN 0-7167-0344-0 .
^ Майкл Вайс; Джон Баэз. «Сохраняется ли энергия в общей теории относительности?» . Проверено 25 апреля 2014 г.
^ Дж. А. Уилер; К. Миснер; К. С. Торн (1973). Гравитация . WH Freeman & Co., стр. 558–559. ISBN 0-7167-0344-0 .

Дальнейшее чтение

Лэмб, Х. (2006) [1932]. Гидродинамика (6-е изд.). Издательство Кембриджского университета. ISBN 978-0-521-45868-9 .
Гриффитс, диджей (1999). Введение в электродинамику (3-е изд.). Pearson Education Inc. ISBN 81-7758-293-3 .
Грант, И.С.; Филлипс, WR (2008). Электромагнетизм . Манчестерская серия по физике (2-е изд.). ISBN 978-0-471-92712-9 .
Уиллер, Дж.А.; Миснер, К.; Торн, Канзас (1973). Гравитация . WH Freeman & Co. ISBN 0-7167-0344-0 .

[Pedlosky-1] Перейти обратно: ^а ^б Педлоски, Джозеф (1987). Геофизическая гидродинамика . Спрингер . стр. 10–13 . ISBN 978-0-387-96387-7 .

[2] Клэнси, LJ (1975), Аэродинамика , Раздел 3.3, Pitman Publishing Limited, Лондон

[Fielding-3] Филдинг, Сюзанна. «Основы гидродинамики» (PDF) . Даремский университет . Проверено 22 декабря 2019 г.

[4] Об этом выводе см., например. МакМахон, Д. (2006). Квантовая механика демистифицирована . МакГроу Хилл. ISBN 0-07-145546-9 .

[5] Д. МакМахон (2006). Демистифицированная теория относительности . МакГроу Хилл (США). ISBN 0-07-145545-0 .

[6] К.В. Миснер; К.С. Торн; Дж. А. Уилер (1973). Гравитация . WH Freeman & Co. ISBN 0-7167-0344-0 .

[7] Майкл Вайс; Джон Баэз. «Сохраняется ли энергия в общей теории относительности?» . Проверено 25 апреля 2014 г.

[8] Дж. А. Уилер; К. Миснер; К. С. Торн (1973). Гравитация . WH Freeman & Co., стр. 558–559. ISBN 0-7167-0344-0 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]