✖


Jump to content

Метод конечных разностей во временной области

В методе конечных разностей во временной области «решетка Йи» используется для дискретизации уравнений Максвелла в пространстве. Эта схема предполагает размещение электрических и магнитных полей на шахматной сетке.

Метод конечных разностей во временной области ( FDTD ) или метод Йи (названный в честь американского математика-прикладника китайского происхождения Кейна С. Йи , родившегося в 1934 году) — метод численного анализа , используемый для моделирования вычислительной электродинамики (нахождения приближенных решений связанной системы дифференциальных уравнений ). . Поскольку это метод во временной области , решения FDTD могут охватывать широкий диапазон частот за один прогон моделирования и естественным образом обрабатывать нелинейные свойства материала.

Метод FDTD принадлежит к общему классу методов дифференциального численного моделирования на основе сетки ( методы конечных разностей ). Зависящие от времени уравнения Максвелла (в форме частных производных ) дискретизируются с использованием центрально-разностных по пространству и времени приближений к частным производным . Полученные конечно-разностные уравнения решаются либо программно, либо аппаратно скачкообразно : компоненты электрического поля вектора в объеме пространства решаются в данный момент времени; затем компоненты вектора магнитного поля в том же пространственном объеме решаются в следующий момент времени; и этот процесс повторяется снова и снова, пока желаемое переходное или установившееся поведение электромагнитного поля не будет полностью развито.

История

[ редактировать ]

Конечно-разностные схемы для нестационарных уравнений в частных производных (ЧДУ) уже много лет используются в задачах вычислительной гидродинамики . [1] включая идею использования центрированных конечно-разностных операторов на разнесенных сетках в пространстве и времени для достижения точности второго порядка. [1] Новизна схемы FDTD Кейна Йи, представленная в его основополагающей статье 1966 года, [2] заключалась в применении центрированных конечно-разностных операторов на разнесенных сетках в пространстве и времени для каждого компонента электрического и магнитного векторного поля в уравнениях ротора Максвелла.Дескриптор «Временная область с конечной разностью» и соответствующая ему аббревиатура «FDTD» были предложены Алленом Тафловом в 1980 году. [3] Примерно с 1990 года методы FDTD стали основным средством компьютерного моделирования многих научных и инженерных задач, связанных с взаимодействием электромагнитных волн с материальными структурами. Текущие приложения моделирования FDTD варьируются от ближнего постоянного тока (сверхнизкочастотная геофизика, охватывающая весь волновод Земля -ионосфера ) через микроволны (технология радиолокационной сигнатуры, антенны , устройства беспроводной связи, цифровые межсоединения, биомедицинская визуализация/лечение) и видимого света ( фотонные кристаллы , наноплазмоника биофотоника , солитоны и . ) [4] В 2006 году в научной и инженерной литературе появилось около 2000 публикаций, связанных с FDTD (см. « Популярность »). По состоянию на 2013 год существует не менее 25 поставщиков коммерческого/собственного программного обеспечения FDTD; 13 по бесплатному/ открытому проектов FDTD программному обеспечению; и 2 бесплатно распространяемых проекта FDTD с закрытым исходным кодом, некоторые из которых не предназначены для коммерческого использования (см. Внешние ссылки ).

Разработка FDTD и уравнений Максвелла

[ редактировать ]

Понимание основы, технического развития и возможного будущего численных методов FDTD для уравнений Максвелла можно получить, сначала рассмотрев их историю. Ниже перечислены некоторые ключевые публикации в этой области.

Частичная хронология методов FDTD и приложений для уравнений Максвелла. [5]
год событие
1928 Курант, Фридрихс и Леви (CFL) публикуют плодотворную статью, в которой открыта условная устойчивость явных нестационарных конечно-разностных схем, а также классической схемы FD для решения волнового уравнения второго порядка в 1-D и 2-D. [6]
1950 Первое появление метода фон Неймана анализа устойчивости для неявных/явных нестационарных методов конечных разностей. [7]
1966 Йи описал численный метод FDTD для решения уравнений ротора Максвелла на сетках, разнесенных в пространстве и времени. [2]
1969 Лам сообщил о правильном численном условии устойчивости CFL для алгоритма Йи, используя анализ устойчивости фон Неймана. [8]
1975 Тафлов и Бродвин сообщили о первых синусоидальных стационарных FDTD-решениях двух- и трехмерных взаимодействий электромагнитных волн с материальными структурами; [9] и первые модели биоэлектромагнетизма. [10]
1977 Холланд, Кунц и Ли применили алгоритм Йи к проблемам ЭМИ. [11] [12]
1980 Тафлав придумал аббревиатуру FDTD и опубликовал первые проверенные модели FDTD проникновения синусоидальной стационарной электромагнитной волны в трехмерную металлическую полость. [3]
1981 Мур опубликовал первое численно устойчивое поглощающее граничное условие второго порядка точности (ABC) для сетки Йи. [13]
1982–83 Тафлов и Умашанкар разработали первые модели рассеяния электромагнитных волн FDTD, вычисляющие синусоидальные стационарные ближние поля, дальние поля и поперечное сечение радара для двух- и трехмерных структур. [14] [15]
1984 Ляо и др. сообщили об улучшенном ABC, основанном на пространственно-временной экстраполяции поля, прилегающего к внешней границе сетки. [16]
1985 Гварек представил формулировку эквивалентной схемы с сосредоточенными параметрами FDTD. [17]
1986 Чой и Хефер опубликовали первое моделирование волноводных структур с помощью FDTD. [18]
1987–88 Кригсманн и др. и Мур и др. опубликовали первые статьи по теории ABC в журнале IEEE Transactions on Antennas and Propagation . [19] [20]
1987–88, 1992 Методы субъячеек контурного пути были представлены Умашанкаром и др., чтобы обеспечить FDTD-моделирование тонких проводов и пучков проводов. [21] Тафлав и др. для моделирования проникновения через трещины в проводящих экранах, [22] и Юргенса и др. для конформного моделирования поверхности плавно изогнутого рассеивателя. [23]
1988 Салливан и др. опубликовали первую трехмерную FDTD-модель поглощения синусоидальных стационарных электромагнитных волн всем человеческим телом. [24]
1988 FDTD-моделирование микрополосок было предложено Zhang et al . [25]
1990–91 FDTD-моделирование частотно-зависимой диэлектрической проницаемости было предложено Кашива и Фукаи. [26] Любберс и др . [27] и Джозеф и др . [28]
1990–91 Моделирование антенн FDTD было предложено Мэлони и др . [29] Кац и др ., [30] и Тиркас и Баланис. [31]
1990 FDTD-моделирование пикосекундных оптоэлектронных переключателей было предложено Сано и Сибатой. [32] и Эль-Газали и др . [33]
1992–94 Было представлено FDTD-моделирование распространения оптических импульсов в средах с нелинейной дисперсией, включая первые временные солитоны в одном измерении Гурджианом и Тафловом; [34] самофокусировка луча по Циолковскому и Джадкинсу; [35] первые временные солитоны в двух измерениях Джозефа и др .; [36] и первые пространственные солитоны в двух измерениях Джозефа и Тафлава. [37]
1992 FDTD-моделирование элементов электронных схем с сосредоточенными параметрами было предложено Sui et al . [38]
1993 Толанд и др. опубликовали первые FDTD-модели устройств усиления (туннельные диоды и диоды Ганна), возбуждающих резонаторы и антенны. [39]
1993 Аояги и др. представляют гибридный алгоритм Йи/уравнение скалярной волны и демонстрируют эквивалентность схемы Йи схеме конечных разностей для уравнения электромагнитных волн . [40]
1994 Томас и др. представили эквивалентную схему Нортона для пространственной решетки FDTD, которая позволяет инструменту анализа цепей SPICE реализовывать точные подсеточные модели нелинейных электронных компонентов или полные схемы, встроенные в решетку. [41]
1994 Беренджер представил высокоэффективную систему ABC с идеально согласованными слоями (PML) для двумерных сеток FDTD. [42] который был расширен до неортогональных сеток Наварро и др ., [43] и три измерения Каца и др ., [44] и дисперсионным окончаниям волноводов Reuter et al . [45]
1994 Чу и Уидон представили PML растяжения координат, который легко расширяется до трех измерений, других систем координат и других физических уравнений. [46]
1995–96 Сакс и др. и Гедни представили физически реализуемый одноосный идеально согласованный слой (UPML) ABC. [47] [48]
1997 Лю представил метод псевдоспектральной временной области (PSTD), который позволяет осуществлять чрезвычайно грубую пространственную выборку электромагнитного поля на пределе Найквиста. [49]
1997 Рамахи представил метод дополнительных операторов (COM) для реализации высокоэффективных аналитических ABC. [50]
1998 Мэлони и Кеслер представили несколько новых способов анализа периодических структур в пространственной решетке FDTD. [51]
1998 Награ и Йорк представили гибридную FDTD-квантово-механическую модель взаимодействия электромагнитных волн с материалами, в которых электроны переходят между несколькими энергетическими уровнями. [52]
1998 Хагнесс и др. представили FDTD-моделирование обнаружения рака молочной железы с использованием методов сверхширокополосного радара. [53]
1999 Шнайдер и Вагнер представили комплексный анализ дисперсии сетки FDTD на основе комплексных волновых чисел. [54]
2000–01 Чжэн, Чен и Чжан представили первый трехмерный неявный алгоритм FDTD с чередованием направлений (ADI) с доказуемой безусловной численной устойчивостью. [55] [56]
2000 Роден и Гедни представили усовершенствованную сверточную систему PML (CPML) ABC. [57]
2000 Райландер и Бондесон представили доказуемо стабильный FDTD - гибридный метод конечных элементов во временной области. [58]
2002 Хаякава и др. , а также Симпсон и Тафлов независимо друг от друга представили FDTD-моделирование глобального волновода Земля-ионосфера для чрезвычайно низкочастотных геофизических явлений. [59] [60]
2003 ДеРэдт представил безусловно стабильную, «одношаговую» технику FDTD. [61]
2004 Сориано и Наварро вывели условие устойчивости метода Quantum FDTD. [62]
2008 Ахмед, Чуа, Ли и Чен представили трехмерный локально-одномерный (LOD)метод FDTD и доказали безусловную численную устойчивость. [63]
2008 Танигучи, Баба, Нагаока и Аметани представили представление тонкого провода для вычислений FDTD для проводящих сред. [64]
2009 Оливейра и Собриньо применили метод FDTD для моделирования ударов молнии на силовой подстанции. [65]
2012 Моксли и др. разработали обобщенный квантовый метод с конечной разностью во временной области для гамильтониана, взаимодействующего с N телами. [66]
2013 Моксли и др. разработали обобщенную конечно-разностную схему во временной области для решения нелинейных уравнений Шредингера. [67]
2014 Моксли и др. разработали неявную обобщенную конечно-разностную схему во временной области для решения нелинейных уравнений Шредингера. [68]
2021 Оливейра и Пайва разработали метод наименьших квадратов конечной разности во временной области (LS-FDTD) для использования временных шагов за пределами предела FDTD CFL. [69]

Модели и методы FDTD

[ редактировать ]

Если рассмотреть дифференциальные уравнения Максвелла , можно увидеть, что изменение E-поля во времени (производная по времени) зависит от изменения H-поля в пространстве (ротор ) . Это приводит к базовому соотношению временного шага FDTD, согласно которому в любой точке пространства обновленное значение E-поля во времени зависит от сохраненного значения E-поля и числового ротора локального распределения H. -поле в космосе. [2]

H-поле изменяется по времени аналогичным образом. В любой точке пространства обновленное значение H-поля во времени зависит от сохраненного значения H-поля и числового ротора локального распределения E-поля в пространстве. Итерация обновлений E-поля и H-поля приводит к процессу, идущему во времени, в котором аналоги дискретных данных рассматриваемых непрерывных электромагнитных волн распространяются в числовой сетке, хранящейся в памяти компьютера.

Иллюстрация стандартной декартовой ячейки Йи, используемой для FDTD, вокруг которой распределены компоненты вектора электрического и магнитного поля. [2] Визуализированные в виде кубического вокселя , компоненты электрического поля образуют ребра куба, а компоненты магнитного поля — нормали к граням куба. Трехмерная пространственная решетка состоит из множества таких ячеек Йи. Структура взаимодействия электромагнитных волн отображается в пространственной решетке путем присвоения соответствующих значений диэлектрической проницаемости каждому компоненту электрического поля и проницаемости каждому компоненту магнитного поля.

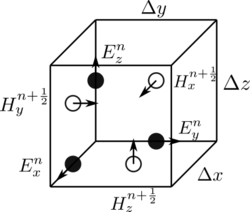
Это описание справедливо для методов 1-D, 2-D и 3-D FDTD. Если учитывать несколько измерений, вычисление числового ротора может усложниться. В основополагающей статье Кейна Йи 1966 года было предложено пространственно расположить векторные компоненты E-поля и H-поля вокруг прямоугольных элементарных ячеек декартовой вычислительной сетки так, чтобы каждый компонент вектора E-поля располагался посередине между парой компонентов вектора H-поля, и наоборот. [2] Эта схема, теперь известная как решетка Йи , оказалась очень надежной и остается в основе многих современных программных конструкций FDTD.

Кроме того, Йи предложил схему чехарды для движения во времени, в которой обновления E-поля и H-поля расположены в шахматном порядке, так что обновления E-поля выполняются в середине каждого временного шага между последовательными обновлениями H-поля, и наоборот. [2] С другой стороны, эта явная схема временного шага позволяет избежать необходимости одновременного решения уравнений и, кроме того, обеспечивает численное распространение волн без диссипации. С другой стороны, эта схема требует верхней границы временного шага для обеспечения численной стабильности. [9] В результате для завершения некоторых классов моделирования могут потребоваться многие тысячи временных шагов.

Использование метода FDTD

[ редактировать ]

Чтобы реализовать FDTD-решение уравнений Максвелла, сначала необходимо установить вычислительную область. Вычислительная область — это просто физическая область, в которой будет выполняться моделирование. Поля E и H определяются в каждой точке пространства внутри этой вычислительной области. Должен быть указан материал каждой ячейки в расчетной области. Обычно материал представляет собой свободное пространство (воздух), металл или диэлектрик . Можно использовать любой материал, если его проницаемость , диэлектрическая проницаемость и проводимость указаны .

Диэлектрическая проницаемость дисперсионных материалов в табличной форме не может быть напрямую подставлена ​​в схему FDTD.Вместо этого его можно аппроксимировать, используя несколько членов Дебая, Друде, Лоренца или критических точек.Это приближение можно получить с помощью открытых подгоночных программ. [70] и не обязательно имеет физический смысл.

После того как расчетная область и материалы сетки определены, указывается источник. Источником может быть ток в проводе, приложенное электрическое поле или падающая плоская волна.В последнем случае FDTD можно использовать для моделирования рассеяния света от объектов произвольной формы, плоских периодических структур под различными углами падения, [71] [72] и фотонная зонная структура бесконечных периодических структур. [73] [74]

Поскольку поля E и H определяются напрямую, результатом моделирования обычно является поле E или H в точке или серии точек в пределах расчетной области. Моделирование развивает поля E и H вперед во времени.

Обработка может выполняться на полях E и H, возвращаемых моделированием. Обработка данных также может происходить во время моделирования.

Хотя метод FDTD вычисляет электромагнитные поля в компактной пространственной области, рассеянные и/или излучаемые дальние поля могут быть получены посредством преобразований из ближнего поля в дальнее. [14]

Сильные стороны моделирования FDTD

[ редактировать ]

У каждого метода моделирования есть сильные и слабые стороны, и метод FDTD не является исключением.

  • FDTD — это универсальный метод моделирования, используемый для решения уравнений Максвелла. Он интуитивно понятен, поэтому пользователи могут легко понять, как им пользоваться, и знать, чего ожидать от той или иной модели.
  • FDTD — это метод во временной области, и когда в качестве источника используется широкополосный импульс (например, гауссов), то отклик системы в широком диапазоне частот можно получить с помощью одного моделирования. Это полезно в приложениях, где резонансные частоты точно не известны, или в тех случаях, когда требуется широкополосный результат.
  • Поскольку FDTD рассчитывает поля E и H повсюду в вычислительной области по мере их развития во времени, он позволяет обеспечить анимированное отображение движения электромагнитного поля через модель. Этот тип отображения полезен для понимания того, что происходит в модели, и для обеспечения правильной работы модели.
  • Метод FDTD позволяет пользователю указывать материал во всех точках вычислительной области. Можно легко и естественно смоделировать широкий спектр линейных и нелинейных диэлектрических и магнитных материалов.
  • FDTD позволяет напрямую определять влияние апертур. Можно обнаружить экранирующие эффекты, а поля как внутри, так и снаружи конструкции можно обнаружить прямо или косвенно.
  • FDTD напрямую использует поля E и H. Поскольку большинство приложений моделирования EMI/EMC заинтересованы в полях E и H, удобно, что после запуска моделирования не требуется никаких преобразований для получения этих значений.

Слабые стороны моделирования FDTD

[ редактировать ]
Продолжительность: 17 секунд.
Численная дисперсия прямоугольного импульсного сигнала в простой одномерной схеме FDTD. Звенящие артефакты по краям импульса сильно подчеркнуты ( феномен Гиббса ) и сигнал искажается по мере распространения даже при отсутствии дисперсионной среды . Этот артефакт является прямым результатом схемы дискретизации. [4]
  • Поскольку FDTD требует, чтобы вся расчетная область была разбита на сетку, а пространственная дискретизация сетки должна быть достаточно точной, чтобы разрешить как наименьшую длину электромагнитной волны, так и наименьшую геометрическую особенность в модели, можно разработать очень большие вычислительные области, что приводит к очень длинному решению. раз. Модели с длинными тонкими элементами (например, проводами) трудно моделировать в FDTD из-за необходимости слишком большой вычислительной области. Такие методы, как расширение по собственным модам, могут предложить более эффективную альтернативу, поскольку они не требуют мелкой сетки вдоль направления z. [75]
  • Невозможно определить уникальные значения диэлектрической и проницаемости на границе раздела материалов.
  • Шаги по пространству и времени должны удовлетворять условию CFL , иначе интегрирование чехарды, используемое для решения уравнения в частных производных, вероятно, станет нестабильным.
  • FDTD находит поля E/H непосредственно повсюду в вычислительной области. Если желательны значения поля на некотором расстоянии, вполне вероятно, что это расстояние приведет к чрезмерному увеличению расчетной области. Расширения дальней зоны доступны для FDTD, но требуют некоторой постобработки. [4]
  • Поскольку при моделировании FDTD вычисляются поля E и H во всех точках вычислительной области, вычислительная область должна быть конечной, чтобы ее можно было разместить в памяти компьютера. Во многих случаях это достигается путем введения искусственных границ в пространство моделирования. Необходимо позаботиться о том, чтобы свести к минимуму ошибки, вносимые такими границами. Существует ряд доступных высокоэффективных поглощающих граничных условий (ABC) для моделирования бесконечной неограниченной вычислительной области. [4] используется специальный поглощающий «материал», называемый идеально согласованным слоем (PML). Вместо этого в большинстве современных реализаций FDTD для реализации поглощающих границ [42] [47]
  • Поскольку FDTD решается путем распространения полей вперед во временной области, электромагнитный временной отклик среды должен моделироваться явно. Для произвольного отклика это требует дорогостоящей в вычислительном отношении временной свертки, хотя в большинстве случаев временной отклик среды (или дисперсии (оптики) ) можно адекватно и просто смоделировать, используя либо метод рекурсивной свертки (RC), либо вспомогательное дифференциальное уравнение (ADE) или метод Z-преобразования. Альтернативным способом решения уравнений Максвелла , который позволяет легко обрабатывать произвольную дисперсию, является псевдоспектральная пространственная область (PSSD) , которая вместо этого распространяет поля вперед в пространстве.

Методы усечения сетки

[ редактировать ]

Наиболее часто используемые методы усечения сетки для задач моделирования FDTD в открытой области - это поглощающее граничное условие Mur (ABC), [13] азбука Ляо, [16] и различные составы идеально подобранных слоев (PML). [4] [43] [42] [47] Методы Мура и Ляо проще, чем PML. Однако PML (который технически является поглощающей областью, а не граничным условием как таковым ) может обеспечить отражения на порядки ниже. Понятие PML было введено Ж.-П. Беренджер в плодотворной статье 1994 года в Журнале вычислительной физики. [42] С 1994 года первоначальная реализация разделенного поля Беренджера была модифицирована и расширена до одноосного PML (UPML), сверточного PML (CPML) и PML высшего порядка. Последние две формулировки PML обладают повышенной способностью поглощать затухающие волны и, следовательно, в принципе могут быть помещены ближе к моделируемой рассеивающей или излучающей структуре, чем исходная формулировка Беренджера.

Чтобы уменьшить нежелательное числовое отражение от PML, можно использовать метод дополнительных обратно поглощающих слоев. [76]

Популярность

[ редактировать ]


Несмотря на общее увеличение числа научных публикацийпропускная способность за тот же период и общее расширение интересаво всех методах вычислительной электромагнетики (CEM) естьсемь основных причин огромного роста интереса к FDTDподходы к вычислительному решению уравнений Максвелла:

  1. FDTD не требует инверсии матрицы. Будучи полностью явным вычислением, FDTD позволяет избежать трудностей с матричными инверсиями, которые ограничивают размер моделей интегрального уравнения в частотной области и моделей электромагнетизма конечных элементов обычно менее 10. 9 электромагнитное поле неизвестно. [4] Модели FDTD с количеством до 10 9 неизвестные поля были запущены; у этого числа нет внутренней верхней границы. [4]
  2. FDTD является точным и надежным. Источники ошибок в расчетах FDTD хорошо понятны и могут быть ограничены, что позволяет получить точные модели для очень широкого спектра задач взаимодействия электромагнитных волн. [4]
  3. FDTD естественным образом относится к импульсивному поведению. Будучи методом временной области, FDTD напрямую рассчитывает импульсную характеристику электромагнитной системы. Таким образом, одно моделирование FDTD может обеспечить либо сверхширокополосные временные сигналы, либо синусоидальный установившийся отклик на любой частоте в пределах спектра возбуждения. [4]
  4. FDTD естественно рассматривает нелинейное поведение. Будучи методом временной области, FDTD напрямую рассчитывает нелинейный отклик электромагнитной системы. Это позволяет естественным образом объединить FDTD с наборами вспомогательных дифференциальных уравнений, которые описывают нелинейности как с классической, так и с полуклассической точки зрения. [4] Одним из направлений исследований является разработка гибридных алгоритмов, которые объединяют модели классической электродинамики FDTD с явлениями, возникающими из квантовой электродинамики, особенно с флуктуациями вакуума, такими как эффект Казимира . [4] [77]
  5. FDTD – это системный подход. При использовании FDTD определение новой моделируемой структуры сводится к проблеме построения сетки, а не к потенциально сложной переформулировке интегрального уравнения. Например, FDTD не требует расчета структурно-зависимых функций Грина. [4]
  6. Компьютерные архитектуры с параллельной обработкой стали доминировать в суперкомпьютерах. FDTD с высокой эффективностью масштабируется на компьютерах с параллельными процессорами и очень хорошо с недавно разработанной технологией ускорителей на базе графических процессоров. [4]
  7. Возможности компьютерной визуализации быстро растут. Хотя эта тенденция положительно влияет на все численные методы, она имеет особое преимущество для методов FDTD, которые генерируют временные массивы величин поля, подходящие для использования в цветных видеороликах для иллюстрации динамики поля. [4]

Тафлав утверждает, что совокупность этих факторов позволяет предположить, что FDTD останется одним издоминирующие методы вычислительной электродинамики (а также, возможно, другие мультифизические задачи). [4]

См. также

[ редактировать ]

Ссылки

[ редактировать ]
  1. ^ Перейти обратно: а б Дж. фон Нейман; Р.Д. Рихтмайер (март 1950 г.). «Метод численного расчета гидродинамических ударов». Журнал прикладной физики . 21 (3): 232–237. Бибкод : 1950JAP....21..232В . дои : 10.1063/1.1699639 .
  2. ^ Перейти обратно: а б с д и ж Кейн Йи (1966). «Численное решение начально-краевых задач с уравнениями Максвелла в изотропных средах». Транзакции IEEE по антеннам и распространению . 14 (3): 302–307. Бибкод : 1966ITAP...14..302Y . дои : 10.1109/TAP.1966.1138693 . S2CID   122712881 .
  3. ^ Перейти обратно: а б А. Тафлов (1980). «Применение метода конечных разностей во временной области к задачам синусоидального стационарного электромагнитного проникновения» (PDF) . IEEE Транс. Электромагн. Совместим. 22 (3): 191–202. Бибкод : 1980ITElC..22..191T . дои : 10.1109/TEMC.1980.303879 . S2CID   39236486 .
  4. ^ Перейти обратно: а б с д и ж г час я дж к л м н тот Аллен Тафлав и Сьюзан К. Хэгнесс (2005). Вычислительная электродинамика: метод конечных разностей во временной области, 3-е изд . Издательство «Артех Хаус». ISBN  978-1-58053-832-9 .
  5. ^ Адаптировано с разрешения Тафлова и Хагнесса (2005).
  6. ^ Ричард Курант; Курт Отто Фридрихс; Ганс Леви (1928). «Об уравнениях в частных производных математической физики» . Математические анналы (на немецком языке). 100 (1): 32–74. Стартовый код : 1928МатАн.100...32С . дои : 10.1007/BF01448839 . ЖФМ   54.0486.01 . МР1512478   . S2CID   120760331 .
  7. ^ Г. Г. О'Брайен, М. А. Хайман и С. Каплан (1950). «Исследование численного решения уравнений в частных производных». Журнал математической физики . 29 (1): 223–251. дои : 10.1002/sapm1950291223 . МР   0040805 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
  8. ^ Донг-Хоа Лам (1969). «Методы конечных разностей для решения задач электромагнитного рассеяния» (PDF) . Государственный университет Миссисипи, Заметки о взаимодействии . 44 .
  9. ^ Перейти обратно: а б А. Тафлов; М. Е. Бродвин (1975). «Численное решение стационарных задач электромагнитного рассеяния с использованием нестационарных уравнений Максвелла» (PDF) . Транзакции IEEE по теории и технике микроволнового излучения . 23 (8): 623–630. Бибкод : 1975ITMTT..23..623T . дои : 10.1109/TMTT.1975.1128640 .
  10. ^ А. Тафлов; М. Е. Бродвин (1975). «Расчет электромагнитных полей и индуцированных температур в модели человеческого глаза, облученного микроволновым излучением» (PDF) . Транзакции IEEE по теории и технике микроволнового излучения . 23 (11): 888–896. Бибкод : 1975ITMTT..23..888T . дои : 10.1109/TMTT.1975.1128708 .
  11. ^ Р. Холланд (1977). «Треда: код связи и рассеяния ЭМИ в свободном поле». Транзакции IEEE по ядерной науке . 24 (6): 2416–2421. Бибкод : 1977ITNS...24.2416H . дои : 10.1109/TNS.1977.4329229 . S2CID   35395821 .
  12. ^ К.С. Кунц; К.М. Ли (1978). «Трехмерное конечно-разностное решение внешней реакции самолета на сложную переходную электромагнитную среду». IEEE Транс. Электромагн. Совместим. 20 (2): 333–341. дои : 10.1109/TEMC.1978.303727 . S2CID   31666283 .
  13. ^ Перейти обратно: а б Г. Мур (1981). «Поглощающие граничные условия для конечно-разностной аппроксимации уравнений электромагнитного поля во временной области». IEEE Транс. Электромагн. Совместим. 23 (4): 377–382. дои : 10.1109/TEMC.1981.303970 . S2CID   25768246 .
  14. ^ Перейти обратно: а б КР Умашанкар; А. Тафлов (1982). «Новый метод анализа электромагнитного рассеяния сложных объектов» (PDF) . IEEE Транс. Электромагн. Совместим. 24 (4): 397–405. Бибкод : 1982ITElC..24..397U . дои : 10.1109/TEMC.1982.304054 . S2CID   37962500 .
  15. ^ А. Тафлов; КР Умашанкар (1983). «Радиолокационный разрез обычных трехмерных рассеивателей» (PDF) . IEEE Транс. Электромагн. Совместим. 25 (4): 433–440. дои : 10.1109/TEMC.1983.304133 . S2CID   40419955 .
  16. ^ Перейти обратно: а б З.П. Ляо; Х.Л. Вонг; Б.П. Ян; Ю. Ф. Юань (1984). «Передающая граница для анализа переходных волн». Scientia Sinica, серия А. 27 : 1063–1076.
  17. ^ В. Гварек (1985). «Анализ планарной схемы произвольной формы — подход во временной области». Транзакции IEEE по теории и технике микроволнового излучения . 33 (10): 1067–1072. Бибкод : 1985ITMTT..33.1067G . дои : 10.1109/TMTT.1985.1133170 .
  18. ^ Д. Х. Чой; У. Дж. Хофер (1986). «Метод конечных разностей во временной области и его применение к задачам собственных значений». Транзакции IEEE по теории и технике микроволнового излучения . 34 (12): 1464–1470. Бибкод : 1986ITMTT..34.1464C . дои : 10.1109/TMTT.1986.1133564 .
  19. ^ Г. А. Кригсманн; А. Тафлов; КР Умашанкар (1987). «Новая формулировка рассеяния электромагнитных волн с использованием подхода к граничным условиям излучения на поверхности» (PDF) . Транзакции IEEE по антеннам и распространению . 35 (2): 153–161. Бибкод : 1987ITAP...35..153K . дои : 10.1109/TAP.1987.1144062 .
  20. ^ Т.Г. Мур; Ю.Г. Блащак; А. Тафлов; Г. А. Кригсманн (1988). «Теория и применение граничных операторов излучения» (PDF) . Транзакции IEEE по антеннам и распространению . 36 (12): 1797–1812. Бибкод : 1988ITAP...36.1797M . дои : 10.1109/8.14402 .
  21. ^ КР Умашанкар; А. Тафлов; Б. Бекер (1987). «Расчет и экспериментальное подтверждение наведенных токов на связанных проводах в полости произвольной формы» (PDF) . Транзакции IEEE по антеннам и распространению . 35 (11): 1248–1257. Бибкод : 1987ITAP...35.1248U . дои : 10.1109/TAP.1987.1144000 .
  22. ^ А. Тафлов; КР Умашанкар; Б. Бекер; Ф.А. Харфуш; КС Йи (1988). «Подробный FDTD-анализ электромагнитных полей, проникающих в узкие щели и соединения внахлест в толстых проводящих экранах» (PDF) . Транзакции IEEE по антеннам и распространению . 36 (2): 247–257. Бибкод : 1988ITAP...36..247T . дои : 10.1109/8.1102 .
  23. ^ Т.Г. Юргенс; А. Тафлов; КР Умашанкар; Т.Г. Мур (1992). «Моделирование искривленных поверхностей во временной области с конечной разностью» (PDF) . Транзакции IEEE по антеннам и распространению . 40 (4): 357–366. Бибкод : 1992ITAP...40..357J . дои : 10.1109/8.138836 .
  24. ^ Д. М. Салливан; ОП Ганди; А. Тафлов (1988). «Использование метода конечных разностей во временной области для расчета поглощения ЭМ в моделях человека» (PDF) . Транзакции IEEE по биомедицинской инженерии . 35 (3): 179–186. дои : 10.1109/10.1360 . ПМИД   3350546 . S2CID   20350396 .
  25. ^ С. Чжан; Дж. Фанг; К.К. Мэй; Ю. Лю (1988). «Расчет дисперсионных характеристик микрополосок временным методом конечных разностей». Транзакции IEEE по теории и технике микроволнового излучения . 36 (2): 263–267. Бибкод : 1988ITMTT..36..263Z . дои : 10.1109/22.3514 .
  26. ^ Т. Касива; И. Фукай (1990). «Обработка методом FDTD дисперсионных характеристик, связанных с электронной поляризацией». Письма о микроволновых и оптических технологиях . 3 (6): 203–205. дои : 10.1002/mop.4650030606 .
  27. ^ Р. Любберс; Ф. Хунсбергер; К. Кунц; Р. Стэндлер; М. Шнайдер (1990). «Частотно-зависимая формулировка во временной области с конечной разностью для дисперсионных материалов». IEEE Транс. Электромагн. Совместим. 32 (3): 222–227. дои : 10.1109/15.57116 .
  28. ^ Р. М. Джозеф; СК Хагнесс; А. Тафлов (1991). «Прямое интегрирование по времени уравнений Максвелла в средах с линейной дисперсией с поглощением для рассеяния и распространения фемтосекундных электромагнитных импульсов» (PDF) . Оптические письма . 16 (18): 1412–4. Бибкод : 1991OptL...16.1412J . дои : 10.1364/OL.16.001412 . ПМИД   19776986 .
  29. ^ Дж. Г. Мэлони; Г.С. Смит; WR Скотт-младший (1990). «Точный расчет излучения простых антенн с использованием метода конечных разностей во временной области». Транзакции IEEE по антеннам и распространению . 38 (7): 1059–1068. Бибкод : 1990ITAP...38.1059M . дои : 10.1109/8.55618 . S2CID   31583883 .
  30. ^ Д.С. Кац; А. Тафлов ; MJ Пикет-Мэй ; КР Умашанкар (1991). «FDTD-анализ излучения электромагнитных волн от систем, содержащих рупорные антенны» (PDF) . Транзакции IEEE по антеннам и распространению . 39 (8): 1203–1212. Бибкод : 1991ITAP...39.1203K . дои : 10.1109/8.97356 .
  31. ^ П. А. Тиркас; С.А. Баланис (1991). «Метод конечной разности во временной области для излучения рупорных антенн». Симпозиум Общества антенн и распространения радиоволн, 1991 г., дайджест . Том. 3. стр. 1750–1753. дои : 10.1109/APS.1991.175196 . ISBN  978-0-7803-0144-3 . S2CID   122038624 .
  32. ^ Э. Сано; Т. Шибата (1990). «Полноволновой анализ пикосекундных фотопроводящих переключателей». Журнал IEEE по квантовой электронике . 26 (2): 372–377. Бибкод : 1990IJQE...26..372S . дои : 10.1109/3.44970 .
  33. ^ С.М. Эль-Газали; Р.П. Джоши; РО Грондин (1990). «Электромагнитные и транспортные соображения при моделировании субпикосекундного фотопроводящего переключателя». Транзакции IEEE по теории и технике микроволнового излучения . 38 (5): 629–637. Бибкод : 1990ITMTT..38..629E . дои : 10.1109/22.54932 .
  34. ^ Премьер-министр Гурджян; А. Тафлов (1992). «Прямое интегрирование по времени уравнений Максвелла в средах с нелинейной дисперсией для распространения и рассеяния фемтосекундных электромагнитных солитонов» (PDF) . Оптические письма . 17 (3): 180–182. Бибкод : 1992OptL...17..180G . дои : 10.1364/OL.17.000180 . ПМИД   19784268 .
  35. ^ Р.В. Циолковский; Дж. Б. Джадкинс (1993). «Моделирование самофокусировки ультракоротких оптических импульсов в нелинейной керровской среде с конечным временем отклика с помощью полноволновых векторных уравнений Максвелла». Журнал Оптического общества Америки Б. 10 (2): 186–198. Бибкод : 1993JOSAB..10..186Z . дои : 10.1364/JOSAB.10.000186 .
  36. ^ Р. М. Джозеф; Премьер-министр Гурджян; А. Тафлов (1993). «Прямое интегрирование по времени уравнений Максвелла в двумерных диэлектрических волноводах для распространения и рассеяния фемтосекундных электромагнитных солитонов» (PDF) . Оптические письма . 18 (7): 491–3. Бибкод : 1993OptL...18..491J . дои : 10.1364/OL.18.000491 . ПМИД   19802177 .
  37. ^ Р. М. Джозеф; А. Тафлов (1994). «Механизм отклонения пространственных солитонов, указанный с помощью моделирования уравнений Максвелла FDTD» (PDF) . Письма IEEE Photonics Technology . 2 (10): 1251–1254. Бибкод : 1994IPTL....6.1251J . дои : 10.1109/68.329654 . S2CID   46710331 .
  38. ^ В. Суй; Д.А. Кристенсен; CH Дерни (1992). «Распространение двумерного метода FDTD на гибридные электромагнитные системы с активными и пассивными элементами с сосредоточенными параметрами». Транзакции IEEE по теории и технике микроволнового излучения . 40 (4): 724–730. Бибкод : 1992ITMTT..40..724S . дои : 10.1109/22.127522 .
  39. ^ Б. Толанд; Б. Хаушманд; Т. Ито (1993). «Моделирование нелинейных активных областей методом FDTD». IEEE СВЧ и волноводные буквы . 3 (9): 333–335. дои : 10.1109/75.244870 . S2CID   27549555 .
  40. ^ Аояги, штат Пенсильвания; Ли, Дж. Ф.; Миттра, Р. (1993). «Гибридный алгоритм Йи / подход к уравнению скалярной волны». Транзакции IEEE по теории и технике микроволнового излучения . 41 (9): 1593–1600. Бибкод : 1993ITMTT..41.1593A . дои : 10.1109/22.245683 .
  41. ^ В.А. Томас; МЭ Джонс; MJ Пикет-Мэй ; А. Тафлов; Э. Харриган (1994). «Использование схем SPICE с сосредоточенными параметрами в качестве подсеточных моделей для проектирования высокоскоростных электронных схем FDTD» (PDF) . IEEE СВЧ и волноводные буквы . 4 (5): 141–143. дои : 10.1109/75.289516 . S2CID   32905331 .
  42. ^ Перейти обратно: а б с д Дж. Беренджер (1994). «Идеально подобранный слой для поглощения электромагнитных волн» (PDF) . Журнал вычислительной физики . 114 (2): 185–200. Бибкод : 1994JCoPh.114..185B . дои : 10.1006/jcph.1994.1159 .
  43. ^ Перейти обратно: а б Э.А. Наварро; К. Ву; П.Ю. Чунг; Я. Литва (1994). «Применение сверхпоглощающего граничного условия PML к неортогональному методу FDTD». Электронные письма . 30 (20): 1654–1656. Бибкод : 1994ElL....30.1654N . дои : 10.1049/эл:19941139 .
  44. ^ Д.С. Кац; Э.Т. Тиле; А. Тафлов (1994). «Проверка и расширение на три измерения поглощающего граничного условия Беренджера PML для сеток FDTD» (PDF) . IEEE СВЧ и волноводные буквы . 4 (8): 268–270. дои : 10.1109/75.311494 . S2CID   10156811 .
  45. ^ CE Рейтер; Р. М. Джозеф; Э.Т. Тиле; Д.С. Кац; А. Тафлов (1994). «Граничные условия сверхширокополосного поглощения для прекращения волноведущих структур в моделировании FDTD» (PDF) . IEEE СВЧ и волноводные буквы . 4 (10): 344–346. дои : 10.1109/75.324711 . S2CID   24572883 .
  46. ^ туалет Чу; WH Уидон (1994). «Трехмерная идеально согласованная среда из модифицированных уравнений Максвелла с растянутыми координатами». Письма о микроволновых и оптических технологиях . 7 (13): 599–604. Бибкод : 1994MiOTL...7..599C . дои : 10.1002/mop.4650071304 .
  47. ^ Перейти обратно: а б с С.Д. Гедни (1996). «Анизотропный идеально согласованный слой поглощающей среды для усечения решеток FDTD». Транзакции IEEE по антеннам и распространению . 44 (12): 1630–1639. Бибкод : 1996ITAP...44.1630G . дои : 10.1109/8.546249 .
  48. ^ З.С. Сакс; Д.М. Кингсленд; Р. Ли; Дж. Ф. Ли (1995). «Идеально подобранный анизотропный поглотитель для использования в качестве поглощающего граничного условия». Транзакции IEEE по антеннам и распространению . 43 (12): 1460–1463. Бибкод : 1995ITAP...43.1460S . дои : 10.1109/8.477075 .
  49. ^ К. Х. Лю (1997). «Метод псевдоспектрального временного интервала (PSTD): новый алгоритм решения уравнений Максвелла». Международный симпозиум Общества антенн и распространения IEEE, 1997 г. Дайджест . Том. 1. С. 122–125. дои : 10.1109/APS.1997.630102 . ISBN  978-0-7803-4178-4 . S2CID   21345353 .
  50. ^ ОМ Рамахи (1997). «Метод дополнительных операторов в моделировании FDTD». Журнал IEEE «Антенны и распространение» . 39 (6): 33–45. Бибкод : 1997IAPM...39...33R . дои : 10.1109/74.646801 .
  51. ^ Дж. Г. Мэлони; Депутат Кеслер (1998). «Анализ периодических структур». Глава. 6 в разделе «Достижения в области вычислительной электродинамики: метод конечных разностей во временной области», А. Тафлав, редактор, Artech House, Publishers .
  52. ^ АС Награ; Р. А. Йорк (1998). «FDTD-анализ распространения волн в нелинейно поглощающих и усиливающих средах». Транзакции IEEE по антеннам и распространению . 46 (3): 334–340. Бибкод : 1998ITAP...46..334N . дои : 10.1109/8.662652 .
  53. ^ СК Хагнесс; А. Тафлов; Дж. Э. Бриджес (1998). «Двумерный FDTD-анализ импульсной микроволновой конфокальной системы для обнаружения рака молочной железы: датчики с фиксированным фокусом и антенной решеткой» (PDF) . Транзакции IEEE по биомедицинской инженерии . 45 (12): 1470–1479. дои : 10.1109/10.730440 . ПМИД   9835195 . S2CID   6169784 .
  54. ^ Дж. Б. Шнайдер; К. Л. Вагнер (1999). «Возврат к дисперсии FDTD: распространение со скоростью, превышающей скорость света». IEEE СВЧ и волноводные буквы . 9 (2): 54–56. CiteSeerX   10.1.1.77.9132 . дои : 10.1109/75.755044 .
  55. ^ Ф. Чжэнь; З. Чен; Дж. Чжан (2000). «К разработке трехмерного безусловно устойчивого метода конечных разностей во временной области». Транзакции IEEE по теории и технике микроволнового излучения . 48 (9): 1550–1558. Бибкод : 2000ITMTT..48.1550Z . дои : 10.1109/22.869007 .
  56. ^ Ф. Чжэн; З. Чен (2001). «Численный дисперсионный анализ безусловно устойчивого 3-D метода ADI-FDTD». Транзакции IEEE по теории и технике микроволнового излучения . 49 (5): 1006–1009. Бибкод : 2001ITMTT..49.1006Z . дои : 10.1109/22.920165 .
  57. ^ Дж. А. Роден; С.Д. Гедни (2000). «Convolution PML (CPML): эффективная реализация FDTD CFS-PML для произвольных носителей» . Письма о микроволновых и оптических технологиях . 27 (5): 334–339. doi : 10.1002/1098-2760(20001205)27:5<334::AID-MOP14>3.0.CO;2-A . Архивировано из оригинала 5 января 2013 г.
  58. ^ Т. Райландер; А. Бондесон (2000). «Стабильный гибридный метод FDTD-FEM для уравнений Максвелла». Компьютерная физика. Коммуникации . 125 (1–3): 75–82. дои : 10.1016/S0010-4655(99)00463-4 .
  59. ^ М. Хаякава; Т. Оцуяма (2002). «FDTD-анализ распространения СНЧ-волн в моделях неоднородных субионосферных волноводов» . Журнал ACES . 17 : 239–244. Архивировано из оригинала 27 мая 2012 года.
  60. ^ Джей Джей Симпсон; А. Тафлове (2002). «Двумерная FDTD-модель антиподального распространения ELF и Шумановского резонанса Земли» (PDF) . Антенны IEEE и письма о распространении беспроводной связи . 1 (2): 53–56. Бибкод : 2002IAWPL...1...53S . CiteSeerX   10.1.1.694.4837 . дои : 10.1109/LAWP.2002.805123 . S2CID   368964 . Архивировано из оригинала (PDF) 17 июня 2010 г.
  61. ^ Х. Де Рэдт; К. Михильсен; Дж. С. Коле; М. Т. Фигге (2003). «Решение уравнений Максвелла методом Чебышева: одношаговый конечно-разностный алгоритм во временной области». Транзакции IEEE по антеннам и распространению . 51 (11): 3155–3160. arXiv : физика/0208060 . Бибкод : 2003ITAP...51.3155D . дои : 10.1109/TAP.2003.818809 . S2CID   119095479 .
  62. ^ А. Сориано; Э.А. Наварро; Х. Порти; В. Такой (2004). «Анализ метода конечных разностей во временной области для решения уравнения Шредингера для квантовых устройств». Журнал прикладной физики . 95 (12): 8011–8018. Бибкод : 2004JAP....95.8011S . дои : 10.1063/1.1753661 . hdl : 10550/12837 .
  63. ^ И. Ахмед; ЭК Чуа; Е.П. Ли; З. Чен (2008). «Разработка трехмерного безусловно устойчивого метода LOD-FDTD». Транзакции IEEE по антеннам и распространению . 56 (11): 3596–3600. Бибкод : 2008ITAP...56.3596A . дои : 10.1109/TAP.2008.2005544 . S2CID   31351974 .
  64. ^ Танигучи, Ю.; Баба, Ю.; Н. Нагаока; А. Аметани (2008). «Улучшенное представление тонкого провода для вычислений FDTD». Транзакции IEEE по антеннам и распространению . 56 (10): 3248–3252. Бибкод : 2008ITAP...56.3248T . дои : 10.1109/TAP.2008.929447 . S2CID   29617214 .
  65. ^ РМС де Оливейра; CLSS Собриньо (2009). «Вычислительная среда для моделирования ударов молнии на силовой подстанции методом конечных разностей во временной области». Транзакции IEEE по электромагнитной совместимости . 51 (4): 995–1000. дои : 10.1109/TEMC.2009.2028879 .
  66. ^ Ф.И. Моксли III; Т. Бирнс; Ф. Фудзивара; В. Дай (2012). «Обобщенный квантовый метод с конечной разностью во временной области для гамильтониана, взаимодействующего с N телами». Компьютерная физика. Коммуникации . 183 (11): 2434–2440. Бибкод : 2012CoPhC.183.2434M . дои : 10.1016/j.cpc.2012.06.012 .
  67. ^ Ф.И. Моксли III; Д.Т. Чусс; В. Дай (2013). «Обобщенная конечно-разностная схема во временной области для решения нелинейных уравнений Шредингера». Компьютерная физика. Коммуникации . 184 (8): 1834–1841. Бибкод : 2013CoPhC.184.1834M . дои : 10.1016/j.cpc.2013.03.006 .
  68. ^ Фредерик Моксли ; и др. (2014). Современная математика: Математика непрерывных и дискретных динамических систем . Американское математическое общество. ISBN  978-0-8218-9862-8 .
  69. ^ РМС де Оливейра; Р. Р. Пайва (2021). «Министр наименьших квадратов во временной области с использованием конечных разностей». Транзакции IEEE по антеннам и распространению . 69 (9): 6111–6115. Бибкод : 2021ITAP...69.6111D . дои : 10.1109/TAP.2021.3069576 . S2CID   234307029 .
  70. ^ «Подбор диэлектрической функции» .
  71. ^ И. Валуев; А. Дейнега; С. Белоусов (2008). «Итеративный метод анализа периодических структур при наклонном падении в методе конечных разностей во временной области». Опция Летт . 33 (13): 1491–3. Бибкод : 2008OptL...33.1491V . дои : 10.1364/ол.33.001491 . ПМИД   18594675 .
  72. ^ А. Аминян; Ю. Рахмат-Самии (2006). «Спектральный FDTD: новый метод анализа наклонно падающей плоской волны на периодические структуры». Транзакции IEEE по антеннам и распространению . 54 (6): 1818–1825. Бибкод : 2006ITAP...54.1818A . дои : 10.1109/tap.2006.875484 . S2CID   25120679 .
  73. ^ А. Дейнега; С. Белоусов; И. Валуев (2009). «Гибридный матричный метод FDTD для слоистых периодических структур». Опция Летт . 34 (6): 860–2. Бибкод : 2009OptL...34..860D . дои : 10.1364/ол.34.000860 . ПМИД   19282957 . S2CID   27742034 .
  74. ^ Ю. Хао; Р. Миттра (2009). FDTD-моделирование метаматериалов: теория и приложения . Издательство «Артех Хаус».
  75. ^ Д. Галлахер (2008). «Развитие САПР в фотонике» (PDF) . Информационный бюллетень ЛЕОС .
  76. ^ А. Дейнега; И. Валуев (2011). «Длительное поведение поглощающих границ ПМЛ для слоистых периодических структур». Вычислить. Физ. Коммун . 182 (1): 149–151. Бибкод : 2011CoPhC.182..149D . дои : 10.1016/j.cpc.2010.06.006 .
  77. ^ С. Г. Джонсон, « Численные методы расчета взаимодействий Казимира », в журнале Casimir Physics (Д. Далвит, П. Милонни , Д. Робертс и Ф. да Роза, ред.), том. 834 Конспектов лекций по физике , гл. 6, стр. 175–218, Берлин: Springer, июнь 2011 г.

Дальнейшее чтение

[ редактировать ]

Следующая статья в журнале Nature Milestones: Photons иллюстрирует историческое значение метода FDTD в отношении уравнений Максвелла:

Интервью Аллена Тафлава «Численное решение» в тематическом выпуске журнала Nature Photonics за январь 2015 года , посвященном 150-летию публикации уравнений Максвелла. В этом интервью рассказывается о том, как развитие FDTD связано с полуторавековой историей теории электродинамики Максвелла:

Следующие учебники университетского уровня дают хорошее общее введение в метод FDTD:

[ редактировать ]
В Wikimedia Commons есть медиафайлы, связанные с методом конечных разностей во временной области .

Бесплатное программное обеспечение / программное обеспечение с открытым исходным кодом. Проекты FDTD:

  • FDTD++ : расширенное полнофункциональное программное обеспечение FDTD, а также сложные модели материалов и предопределенные подгонки, а также форумы для обсуждения/поддержки и поддержка по электронной почте.
  • openEMS (полностью трехмерная декартова и цилиндрическая градуированная сетка EC-FDTD Solver, написанная на C++, с использованием интерфейса Matlab / Octave )
  • pFDTD (коды 3D C++ FDTD, разработанные Се-Хеоном Кимом)
  • JFDTD (2D/3D C++ FDTD-коды, разработанные Джеффри М. МакМахоном для нанофотоники)
  • WOLFSIM. Архивировано 2 июля 2008 г. в Wayback Machine (NCSU) (2-D).
  • Мип ( MIT , 2D/3D/цилиндрический параллельный FDTD)
  • (Гео-) Радар FDTD
  • bigboy (не поддерживается, файлов выпуска нет. Необходимо получить исходный код из cvs)
  • Параллельные (MPI&OpenMP) коды FDTD на C++ (разработаны Ж. Сабо)
  • Код FDTD на Фортране 90
  • Код FDTD на языке C для 2D-моделирования электромагнитных волн
  • Angora (пакет программного обеспечения 3D-параллельного FDTD, поддерживается Илкером Р. Капоглу)
  • GSvit (3D-решатель FDTD с поддержкой вычислений на видеокартах, написанный на C, доступен графический интерфейс пользователя XSvit)
  • gprMax (с открытым исходным кодом (GPLv3), код моделирования 3D/2D FDTD на Python/Cython, разработанный для георадара, но может использоваться для общего ЭМ-моделирования.)

Бесплатное ПО / проекты FDTD с закрытым исходным кодом (некоторые не для коммерческого использования):

  • EMTL (Electro Magnetic Template Library) (Бесплатная библиотека С++ для электромагнитного моделирования. Текущая версия реализует в основном FDTD).
Retrieved from "https://en.wikipedia.org/w/index.php?title=Finite-difference_time-domain_method&oldid=1231345164"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: cf79e862332aead4ffe880f37c09d829__1719509640
URL1:https://arc.ask3.ru/arc/aa/cf/29/cf79e862332aead4ffe880f37c09d829.html
Заголовок, (Title) документа по адресу, URL1:
Finite-difference time-domain method - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)