Метод конечных разностей

В численном анализе методы конечных разностей ( FDM ) — это класс численных методов решения дифференциальных уравнений путем аппроксимации производных с конечными разностями . Как пространственная область, так и временная область (если применимо) дискретизируются или разбиваются на конечное число интервалов, а значения решения в конечных точках интервалов аппроксимируются путем решения алгебраических уравнений, содержащих конечные разности и значения из близлежащих точек. .

Методы конечных разностей преобразуют обыкновенные дифференциальные уравнения (ОДУ) или уравнения в частных производных (УЧП), которые могут быть нелинейными , в систему линейных уравнений , которые можно решить методами матричной алгебры . Современные компьютеры могут эффективно выполнять эти вычисления линейной алгебры , что, наряду с их относительной простотой реализации, привело к широкому использованию FDM в современном численном анализе. Сегодня FDM являются одним из наиболее распространенных подходов к численному решению УЧП, наряду с методами конечных элементов .

Выведите разностный коэффициент из полинома Тейлора

Для n -кратно дифференцируемой функции по теореме Тейлора разложение в ряд Тейлора задается как $$f(x_{0}+h)=f(x_{0})+{\frac {f'(x_{0})}{1!}}h+{\frac {f^{(2)}(x_{0})}{2!}}h^{2}+\cdots +{\frac {f^{(n)}(x_{0})}{n!}}h^{n}+R_{n}(x),$$

Где н ! обозначает факториал n n , а R _n ( x член, обозначающий разницу между полиномом Тейлора степени ) — остаточный и исходной функцией.

Ниже приведен процесс получения аппроксимации первой производной функции f путем предварительного усечения полинома Тейлора плюс остаток: $$f(x_{0}+h)=f(x_{0})+f'(x_{0})h+R_{1}(x).$$Деление на h дает: $${f(x_{0}+h) \over h}={f(x_{0}) \over h}+f'(x_{0})+{R_{1}(x) \over h}$$Решение для $f'(x_{0})$: $$f'(x_{0})={f(x_{0}+h)-f(x_{0}) \over h}-{R_{1}(x) \over h}.$$

Предполагая, что $R_{1}(x)$ достаточно мала, аппроксимация первой производной f равна: $$f'(x_{0})\approx {f(x_{0}+h)-f(x_{0}) \over h}.$$

Это похоже на определение производной, которое: $$f'(x_{0})=\lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}.$$за исключением предела в ноль (в честь этого назван метод).

Точность и порядок

См. Также: Коэффициент конечной разности.

Погрешность решения метода определяется как разница между приближением и точным аналитическим решением. Двумя источниками ошибок в методах конечных разностей являются ошибка округления , потеря точности из-за компьютерного округления десятичных величин, и ошибка усечения или ошибка дискретизации , разница между точным решением исходного дифференциального уравнения и точной величиной, предполагающей идеальная арифметика (без округления).

Метод конечных разностей основан на дискретизации функции на сетке.

Чтобы использовать метод конечных разностей для аппроксимации решения проблемы, необходимо сначала дискретизировать область задачи. Обычно это делается путем разделения домена на равномерную сетку (см. изображение). Это означает, что методы конечных разностей создают наборы дискретных численных аппроксимаций производной, часто в режиме «шага по времени».

Выражением общего интереса является локальная ошибка усечения метода. Обычно выражаемая с использованием нотации Big-O , локальная ошибка усечения относится к ошибке одного применения метода. То есть это количество $f'(x_{i})-f'_{i}$ если $f'(x_{i})$ относится к точному значению и $f'_{i}$ к численному приближению. Оставшийся член полинома Тейлора можно использовать для анализа локальной ошибки усечения . Используя форму Лагранжа остатка от полинома Тейлора для $f(x_{0}+h)$, что $$R_{n}(x_{0}+h)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}(h)^{n+1}\,,\quad x_{0}<\xi <x_{0}+h,$$может быть обнаружен доминирующий член локальной ошибки усечения. Например, снова используя формулу прямой разности для первой производной, зная, что $f(x_{i})=f(x_{0}+ih)$, $$f(x_{0}+ih)=f(x_{0})+f'(x_{0})ih+{\frac {f''(\xi )}{2!}}(ih)^{2},$$и с некоторыми алгебраическими манипуляциями это приводит к $${\frac {f(x_{0}+ih)-f(x_{0})}{ih}}=f'(x_{0})+{\frac {f''(\xi )}{2!}}ih,$$и далее отметив, что величина слева представляет собой аппроксимацию метода конечных разностей, а величина справа представляет собой точное интересующее количество плюс остаток, очевидно, что этот остаток представляет собой локальную ошибку усечения. Окончательное выражение этого примера и его порядок: $${\frac {f(x_{0}+ih)-f(x_{0})}{ih}}=f'(x_{0})+O(h).$$

В этом случае локальная ошибка усечения пропорциональна размерам шагов. Качество и длительность моделирования решения FDM зависит от выбора уравнения дискретизации и размеров шага (шагов по времени и пространству). Качество данных и продолжительность моделирования значительно увеличиваются при меньшем размере шага. Следовательно, для практического использования необходим разумный баланс между качеством данных и продолжительностью моделирования. Большие временные шаги полезны для увеличения скорости моделирования на практике. Однако слишком большие временные шаги могут привести к нестабильности и повлиять на качество данных.

Критерии фон Неймана и Куранта-Фридрихса-Леви часто оцениваются для определения устойчивости численной модели.

Пример: обыкновенное дифференциальное уравнение

Например, рассмотрим обыкновенное дифференциальное уравнение $$u'(x)=3u(x)+2.$$Метод Эйлера для решения этого уравнения использует коэффициент конечной разности $${\frac {u(x+h)-u(x)}{h}}\approx u'(x)$$аппроксимировать дифференциальное уравнение, сначала подставив его вместо u'(x), а затем применив немного алгебры (умножив обе части на h, а затем прибавив u(x) к обеим частям), чтобы получить $$u(x+h)\approx u(x)+h(3u(x)+2).$$Последнее уравнение представляет собой конечно-разностное уравнение, и решение этого уравнения дает приближенное решение дифференциального уравнения.

Пример: уравнение теплопроводности

Рассмотрим нормализованное уравнение теплопроводности в одном измерении с однородными граничными условиями Дирихле

$${\begin{cases}U_{t}=U_{xx}\\U(0,t)=U(1,t)=0&{\text{(boundary condition)}}\\U(x,0)=U_{0}(x)&{\text{(initial condition)}}\end{cases}}$$

Один из способов численного решения этого уравнения — аппроксимировать все производные конечными разностями. Сначала разделите домен в пространстве, используя сетку. $x_{0},\dots ,x_{J}$ и вовремя с помощью сетки $t_{0},\dots ,t_{N}$. Предположим, что разделение однородно как в пространстве, так и во времени, поэтому разница между двумя последовательными точками пространства будет h , а между двумя последовательными точками времени будет k . Очки

$$u(x_{j},t_{n})=u_{j}^{n}$$

будет представлять численную аппроксимацию $u(x_{j},t_{n}).$

Явный метод

Трафарет для наиболее распространенного явного метода уравнения теплопроводности.

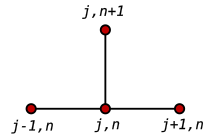
Использование прямой разницы во времени $t_{n}$ второго порядка и центральная разность для пространственной производной в позиции $x_{j}$ ( FTCS ) дает рекуррентное уравнение:

$${\frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={\frac {u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}}{h^{2}}}.$$

Это явный метод решения одномерного уравнения теплопроводности .

Можно получить $u_{j}^{n+1}$ из других значений следующим образом:

$$u_{j}^{n+1}=(1-2r)u_{j}^{n}+ru_{j-1}^{n}+ru_{j+1}^{n}$$

где $r=k/h^{2}.$

Итак, с помощью этого рекуррентного соотношения и зная значения в момент времени n , можно получить соответствующие значения в момент времени n +1. $u_{0}^{n}$ и $u_{J}^{n}$ должны быть заменены граничными условиями, в этом примере они оба равны 0.

Известно, что этот явный метод численно устойчив и сходится всякий раз, когда $r\leq 1/2$. Численные ошибки пропорциональны шагу по времени и квадрату шага по пространству: $$\Delta u=O(k)+O(h^{2})$$

Неявный метод

Неявный метод трафарета.

Использование обратной разницы во времени $t_{n+1}$ и центральная разность второго порядка для пространственной производной в позиции $x_{j}$ (Метод обратного времени и центрированного пространства «BTCS») дает рекуррентное уравнение:

$${\frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={\frac {u_{j+1}^{n+1}-2u_{j}^{n+1}+u_{j-1}^{n+1}}{h^{2}}}.$$

Это неявный метод решения одномерного уравнения теплопроводности .

Можно получить $u_{j}^{n+1}$ от решения системы линейных уравнений:

$$(1+2r)u_{j}^{n+1}-ru_{j-1}^{n+1}-ru_{j+1}^{n+1}=u_{j}^{n}$$

Схема всегда численно устойчива и сходится, но обычно более интенсивна в численном отношении, чем явный метод, поскольку требует решения системы числовых уравнений на каждом временном шаге. Ошибки линейны по времени и квадратичны по пространству: $$\Delta u=O(k)+O(h^{2}).$$

Метод Кранка – Николсона

Наконец, используя центральную разность во времени $t_{n+1/2}$ и центральная разность второго порядка для пространственной производной в позиции $x_{j}$ («CTCS») дает рекуррентное уравнение:

$${\frac {u_{j}^{n+1}-u_{j}^{n}}{k}}={\frac {1}{2}}\left({\frac {u_{j+1}^{n+1}-2u_{j}^{n+1}+u_{j-1}^{n+1}}{h^{2}}}+{\frac {u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}}{h^{2}}}\right).$$

Эта формула известна как метод Кранка-Николсона .

Трафарет Крэнка – Николсона.

Можно получить $u_{j}^{n+1}$ от решения системы линейных уравнений:

$$(2+2r)u_{j}^{n+1}-ru_{j-1}^{n+1}-ru_{j+1}^{n+1}=(2-2r)u_{j}^{n}+ru_{j-1}^{n}+ru_{j+1}^{n}$$

Схема всегда численно устойчива и сходится, но обычно более интенсивна в числовом отношении, поскольку требует решения системы числовых уравнений на каждом временном шаге. Ошибки квадратичны как по временному, так и по пространственному шагу: $$\Delta u=O(k^{2})+O(h^{2}).$$

Сравнение

Подводя итог, можно сказать, что обычно схема Кранка – Николсона является наиболее точной схемой для малых шагов по времени. Для больших временных шагов неявная схема работает лучше, поскольку она требует меньше вычислительных затрат. Явная схема наименее точна и может быть нестабильной, но она также наиболее проста в реализации и наименее трудоемка.

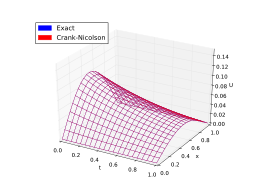
Вот пример. На рисунках ниже представлены решения, полученные вышеуказанными методами для аппроксимации уравнения теплопроводности.

$$U_{t}=\alpha U_{xx},\quad \alpha ={\frac {1}{\pi ^{2}}},$$

с граничным условием

$$U(0,t)=U(1,t)=0.$$

Точное решение

$$U(x,t)={\frac {1}{\pi ^{2}}}e^{-t}\sin(\pi x).$$

Сравнение методов конечных разностей

Явный метод ( не стабильный)

Неявный метод (стабильный)

Метод Кранка-Николсона (стабильный)

Пример: оператор Лапласа

(Непрерывный) оператор Лапласа в $n$-размеры даны $\Delta u(x)=\sum _{i=1}^{n}\partial _{i}^{2}u(x)$.Дискретный оператор Лапласа $\Delta _{h}u$ зависит от размера $n$.

В 1D оператор Лапласа аппроксимируется как $$\Delta u(x)=u''(x)\approx {\frac {u(x-h)-2u(x)+u(x+h)}{h^{2}}}=:\Delta _{h}u(x)\,.$$Это приближение обычно выражается через следующий трафарет $$\Delta _{h}={\frac {1}{h^{2}}}{\begin{bmatrix}1&-2&1\end{bmatrix}}$$и который представляет собой симметричную трехдиагональную матрицу. Для эквидистантной сетки получается матрица Теплица .

Двумерный случай демонстрирует все характеристики более общего n-мерного случая. Каждую вторую частную производную необходимо аппроксимировать аналогично случаю 1D. $${\begin{aligned}\Delta u(x,y)&=u_{xx}(x,y)+u_{yy}(x,y)\\&\approx {\frac {u(x-h,y)-2u(x,y)+u(x+h,y)}{h^{2}}}+{\frac {u(x,y-h)-2u(x,y)+u(x,y+h)}{h^{2}}}\\&={\frac {u(x-h,y)+u(x+h,y)-4u(x,y)+u(x,y-h)+u(x,y+h)}{h^{2}}}\\&=:\Delta _{h}u(x,y)\,,\end{aligned}}$$который обычно задается следующим трафаретом $$\Delta _{h}={\frac {1}{h^{2}}}{\begin{bmatrix}&1\\1&-4&1\\&1\end{bmatrix}}\,.$$

Последовательность

Непротиворечивость упомянутого приближения можно показать для весьма регулярных функций, таких как $u\in C^{4}(\Omega )$.Заявление $$\Delta u-\Delta _{h}u={\mathcal {O}}(h^{2})\,.$$

Чтобы доказать это, необходимо заменить разложение в ряд Тейлора до третьего порядка в дискретный оператор Лапласа.

Характеристики

Субгармоника

Подобно непрерывным субгармоническим функциям, можно определить субгармонические функции для конечно-разностных аппроксимаций. $u_{h}$$$-\Delta _{h}u_{h}\leq 0\,.$$

Среднее значение

можно определить Общий трафарет положительного типа через $${\begin{bmatrix}&\alpha _{N}\\\alpha _{W}&-\alpha _{C}&\alpha _{E}\\&\alpha _{S}\end{bmatrix}}\,,\quad \alpha _{i}>0\,,\quad \alpha _{C}=\sum _{i\in \{N,E,S,W\}}\alpha _{i}\,.$$

Если $u_{h}$ следующее свойство среднего значения является (дискретным) субгармоническим, то выполняется $$u_{h}(x_{C})\leq {\frac {\sum _{i\in \{N,E,S,W\}}\alpha _{i}u_{h}(x_{i})}{\sum _{i\in \{N,E,S,W\}}\alpha _{i}}}\,,$$где аппроксимация оценивается в точках сетки, а трафарет предполагается положительным типом.

Аналогичное свойство среднего значения справедливо и для непрерывного случая.

Принцип максимума

Для (дискретной) субгармонической функции $u_{h}$ имеет место следующее $$\max _{\Omega _{h}}u_{h}\leq \max _{\partial \Omega _{h}}u_{h}\,,$$где $\Omega _{h},\partial \Omega _{h}$ являются дискретизациями непрерывной области $\Omega$, соответственно граница $\partial \Omega$.

Аналогичный принцип максимума справедлив и для непрерывного случая.

Метод SBP-SAT

Метод SBP-SAT ( суммирование по частям — член одновременной аппроксимации в частных производных ) — это стабильный и точный метод дискретизации и наложения граничных условий корректного уравнения с использованием конечных разностей высокого порядка.

Метод основан на конечных разностях, где операторы дифференцирования обладают свойствами суммирования по частям . Обычно эти операторы состоят из матриц дифференцирования с центральными разностными трафаретами внутри и тщательно выбранными односторонними граничными трафаретами, предназначенными для имитации интегрирования по частям в дискретной настройке. При использовании метода SAT граничные условия PDE накладываются слабо, при этом граничные значения «подтягиваются» к желаемым условиям, а не точно выполняются. Если параметры настройки (присущие методу SAT) выбраны правильно, результирующая система ОДУ будет демонстрировать такое же энергетическое поведение, как и непрерывное УЧП, т.е. система не имеет нефизического роста энергии. схема интегрирования с областью устойчивости, включающей части мнимой оси, например метод Рунге-Кутты Это гарантирует стабильность, если используется четвертого порядка. Это делает метод SAT привлекательным методом наложения граничных условий для методов конечных разностей более высокого порядка, в отличие, например, от метода инъекции, который обычно не будет устойчивым, если используются операторы дифференцирования высокого порядка.

См. также

• Метод конечных элементов
• Конечная разница
• Временная область конечной разности
• Метод бесконечной разности
• Трафарет (численный анализ)
• Коэффициенты конечных разностей
• Пятиточечный трафарет
• Теорема Лакса – Рихтмайера
• Методы конечных разностей для ценообразования опционов
• Разностная схема против ветра для конвекции
• Центральная разностная схема
• Дискретное уравнение Пуассона
• Дискретный оператор Лапласа

Дальнейшее чтение

• К. В. Мортон и Д. Ф. Майерс, Численное решение уравнений в частных производных, Введение . Издательство Кембриджского университета, 2005.
• Аутар Кау и Э. Эрик Калу, Численные методы с приложениями , (2008) [1] . Содержит краткое инженерно-ориентированное введение в FDM (для ODE) в главе 08.07 .
• Джон Стрикверда (2004). Конечно-разностные схемы и уравнения в частных производных (2-е изд.). СИАМ. ISBN  978-0-89871-639-9 .
• Смит, Г.Д. (1985), Численное решение уравнений в частных производных: методы конечных разностей, 3-е изд. , Издательство Оксфордского университета
• Питер Олвер (2013). Введение в уравнения в частных производных . Спрингер. Глава 5: Конечные разности. ISBN  978-3-319-02099-0 . .
• Рэндалл Дж. Левек , Конечно-разностные методы для обыкновенных и частных дифференциальных уравнений , SIAM, 2007.
• Сергей Лемешевский, Петр Матус, Дмитрий Поляков (редакторы): «Точные конечно-разностные схемы», Де Грюйтер (2016). DOI: https://doi.org/10.1515/9783110491326 .