Коэффициент сжимаемости

В термодинамике коэффициент сжимаемости ( Z ), также известный как коэффициент сжатия или коэффициент отклонения газа , описывает отклонение реального газа от поведения идеального газа . Его просто определяют как отношение молярного объема газа к молярному объему идеального газа при тех же температуре и давлении . Это полезное термодинамическое свойство для изменения закона идеального газа с учетом поведения реального газа. ^[1] В общем, отклонение от идеального поведения становится тем более значительным, чем ближе газ к фазовому переходу , чем ниже температура или больше давление. Значения коэффициента сжимаемости обычно получают путем расчета на основе уравнений состояния (EOS), таких как уравнение вириала , которые в качестве входных данных принимают эмпирические константы , специфичные для конкретного соединения . Для газа, который представляет собой смесь двух или более чистых газов (например, воздуха или природного газа), состав газа . перед расчетом сжимаемости необходимо знать
Альтернативно, коэффициент сжимаемости конкретных газов можно узнать из обобщенных диаграмм сжимаемости. ^[1] этот сюжет $Z$ как функция давления при постоянной температуре.

Коэффициент сжимаемости не следует путать со сжимаемостью (также известной как коэффициент сжимаемости или изотермической сжимаемости ) материала, которая является мерой относительного изменения объема жидкости или твердого тела в ответ на изменение давления.

Определение и физическое значение

Коэффициент сжимаемости часто определяется в термодинамике и технике как:

Z={\frac {p}{\rho R_{\text{specific}}T}},

где р — давление, $\rho$ плотность газа и ${\textstyle R_{\text{specific}}={\frac {R}{M}}}$ — удельная газовая постоянная , ^[2] $M$ являющийся молярной массой , а $T$ — абсолютная температура ( по шкале Кельвина или Ренкина ).

В статистической механике это описание:

Z={\frac {pV}{nRT}}

где p – давление, n – количество молей газа, $T$ – абсолютная температура , а $R$ – газовая постоянная , В – единица объема

Для идеального газа коэффициент сжимаемости равен $Z=1$ по определению. Во многих реальных приложениях требования к точности требуют учета отклонений от идеального поведения газа, т.е. газа реального поведения . Стоимость $Z$ обычно увеличивается с давлением и уменьшается с температурой. При высоких давлениях молекулы сталкиваются чаще. Это позволяет силам отталкивания между молекулами оказывать заметное влияние, делая молярный объем реального газа ( $V_{\mathrm {m} }$ ) больше молярного объема соответствующего идеального газа ( $(V_{\mathrm {m} })_{\text{ideal gas}}=RT/p$ ), что вызывает $Z$ превышать единицу. ^[3] Когда давление ниже, молекулы могут свободно двигаться. В этом случае доминируют силы притяжения, что делает $Z<1$ . Чем ближе газ к своей критической точке или температуре кипения, тем больше $Z$ отклоняется от идеального случая.

Летучесть

Коэффициент сжимаемости связан с летучестью соотношением: ^{[ нужна ссылка ]}

f=P\exp \left(\int {\frac {Z-1}{P}}dP\right)

Графики обобщенных коэффициентов сжимаемости чистых газов

Уникальная связь между коэффициентом сжимаемости и приведенной температурой . $T_{r}$ , и пониженное давление , $P_{r}$ , был впервые признан Йоханнесом Дидериком ван дер Ваальсом в 1873 году и известен как принцип двух параметров соответствующих состояний . Принцип соответствующих состояний выражает обобщение о том, что свойства газа, зависящие от межмолекулярных сил, универсальным образом связаны с критическими свойствами газа. Это обеспечивает важнейшую основу для разработки корреляций молекулярных свойств.

Что касается сжимаемости газов, то принцип соответствующих состояний указывает на то, что любой чистый газ при одинаковой приведенной температуре $T_{r}$ и пониженное давление, $P_{r}$ , должен иметь одинаковый коэффициент сжимаемости.

Приведенные температура и давление определяются выражением

T_{r}={\frac {T}{T_{c}}}

и

P_{r}={\frac {P}{P_{c}}}.

Здесь $T_{c}$ и $P_{c}$ называются критической температурой и критическим давлением газа. Это характеристики каждого конкретного газа с $T_{c}$ температура, выше которой невозможно сжижать данный газ и $P_{c}$ — минимальное давление, необходимое для сжижения данного газа при его критической температуре. Вместе они определяют критическую точку жидкости, выше которой не существуют отдельные жидкая и газовая фазы данной жидкости.

Данные давления-объема-температуры (PVT) для реальных газов варьируются от одного чистого газа к другому. Однако, когда коэффициенты сжимаемости различных однокомпонентных газов строятся в зависимости от давления вместе с изотермами температуры, многие графики демонстрируют схожие формы изотерм.

Чтобы получить обобщенный график, который можно использовать для множества различных газов, приведенного давления и температуры, $P_{r}$ и $T_{r}$ , используются для нормализации данных коэффициента сжимаемости. На рисунке 2 приведен пример обобщенного графика коэффициента сжимаемости, полученного на основе сотен экспериментальных точек данных PVT для 10 чистых газов, а именно метана, этана, этилена, пропана, н-бутана, изопентана, н-гексана, азота, диоксида углерода и пар.

Существуют более подробные графики обобщенных коэффициентов сжимаемости, основанные на 25 или более различных чистых газах, например графики Нельсона-Оберта. Говорят, что такие графики имеют точность в пределах 1–2 процентов для $Z$ значения больше 0,6 и в пределах 4–6 процентов для $Z$ значения 0,3–0,6.

Графики обобщенного коэффициента сжимаемости могут иметь значительные ошибки для сильнополярных газов, то есть газов, у которых центры положительного и отрицательного заряда не совпадают. В таких случаях оценка $Z$ ошибка может достигать 15–20 процентов.

Квантовые газы водород, гелий и неон не соответствуют поведению соответствующих состояний, и приведенные давление и температура для этих трех газов должны быть переопределены следующим образом, чтобы повысить точность прогнозирования их коэффициентов сжимаемости при использовании обобщенных графиков:

T_{r}={\frac {T}{T_{c}+8}}

и

P_{r}={\frac {P}{P_{c}+8}}

где температуры указаны в кельвинах, а давление — в атмосферах. ^[4]

Чтение обобщенной диаграммы сжимаемости

Чтобы прочитать диаграмму сжимаемости, необходимо знать приведенное давление и температуру. Если приведенное давление или температура неизвестны, необходимо найти приведенный удельный объем. В отличие от приведенных давления и температуры, приведенный удельный объем не определяется с помощью критического объема. Приведенный удельный объем определяется по формуле:

\nu _{R}={\frac {\nu _{\text{actual}}}{RT_{\text{cr}}/P_{\text{cr}}}}

где $\nu _{\text{actual}}$ это удельный объем. ^[5]

Как только будут найдены два из трех приведенных свойств, можно использовать диаграмму сжимаемости. На диаграмме сжимаемости пониженное давление указано на оси X, а Z — на оси Y. Зная приведенные давление и температуру, найдите заданное давление по оси x. Оттуда двигайтесь вверх по диаграмме, пока не будет найдена заданная пониженная температура. Z можно найти, посмотрев, где пересекаются эти две точки. тот же процесс можно проследить, если уменьшить удельный объем при пониженном давлении или температуре.

Наблюдения, сделанные на основе обобщенной диаграммы сжимаемости

Глядя на обобщенную диаграмму сжимаемости, можно сделать три наблюдения. Эти наблюдения таковы:

Газы ведут себя как идеальный газ независимо от температуры, когда приведенное давление много меньше единицы (P _R ≪ 1).
Когда приведенная температура больше двух (TR _> 2), можно предположить поведение идеального газа независимо от давления, если только давление не намного превышает единицу (P _R ≫ 1).
Газы больше всего отклоняются от поведения идеального газа вблизи критической точки. ^[6]

Теоретические модели

Уравнение вириала особенно полезно для описания причин неидеальности на молекулярном уровне (очень немногие газы являются одноатомными), поскольку оно получено непосредственно из статистической механики:

Z=1+{\frac {B}{V_{\mathrm {m} }}}+{\frac {C}{V_{\mathrm {m} }^{2}}}+{\frac {D}{V_{\mathrm {m} }^{3}}}+\dots

Где коэффициенты в числителе известны как вириальные коэффициенты и являются функциями температуры.

Вириальные коэффициенты учитывают взаимодействия между последовательно увеличивающимися группами молекул. Например, $B$ учитывает взаимодействие пар, $C$ для взаимодействия между тремя молекулами газа и так далее. Поскольку взаимодействия между большим количеством молекул редки, уравнение вириала обычно обрезается после третьего члена. ^[7]

Когда предполагается это усечение, коэффициент сжимаемости связан с потенциалом межмолекулярных сил φ следующим образом:

Z=1+2\pi {\frac {N_{\text{A}}}{V_{\text{m}}}}\int _{0}^{\infty }\left(1-\exp \left({\frac {\varphi }{kT}}\right)\right)r^{2}dr

В статье « Реальный газ» представлены более теоретические методы расчета коэффициентов сжимаемости.

Физический механизм зависимости температуры и давления

Отклонения коэффициента сжимаемости Z от единицы обусловлены межмолекулярными силами притяжения и отталкивания . При заданных температуре и давлении силы отталкивания стремятся увеличить объем, чем у идеального газа; когда эти силы доминируют, Z больше единицы. Когда доминируют силы притяжения, Z меньше единицы. Относительная важность сил притяжения уменьшается с повышением температуры (см. Влияние на газы ).

Как видно выше , поведение Z качественно одинаково для всех газов. Молекулярный азот N ₂ используется здесь для дальнейшего описания и понимания этого поведения. Все данные, используемые в этом разделе, были получены из веб-книги NIST Chemistry WebBook. ^[8] Полезно отметить, что для N ₂ нормальная температура кипения жидкости составляет 77,4 К, а критическая точка находится при 126,2 К и 34,0 бар.

На рисунке справа показан обзор, охватывающий широкий диапазон температур. При низкой температуре (100 К) кривая имеет характерную форму галочки, восходящий участок кривой почти прямо пропорционален давлению. При промежуточной температуре (160 К) наблюдается плавная кривая с широким минимумом; хотя часть высокого давления снова почти линейна, она больше не прямо пропорциональна давлению. Наконец, при высокой температуре (400 К) Z превышает единицу при всех давлениях. Для всех кривых Z приближается к значению идеального газа, равному единице при низком давлении, и превышает это значение при очень высоком давлении.

Чтобы лучше понять эти кривые, на втором рисунке представлено более подробное поведение при низкой температуре и давлении. Все кривые начинаются с Z, равного единице при нулевом давлении, и Z первоначально уменьшается с увеличением давления. N ₂ в этих условиях является газом, поэтому расстояние между молекулами велико, но с ростом давления становится меньше. Это увеличивает притягивающие взаимодействия между молекулами, сближая молекулы и делая объем меньше, чем у идеального газа при той же температуре и давлении. Более высокая температура уменьшает эффект притягивающих взаимодействий, и газ ведет себя более близко к идеальному.

По мере увеличения давления газ в конечном итоге достигает кривой сосуществования газа и жидкости , показанной пунктирной линией на рисунке. Когда это происходит, притягивающие взаимодействия становятся достаточно сильными, чтобы преодолеть тенденцию теплового движения, вызывающего распространение молекул; поэтому газ конденсируется, образуя жидкость. Точки на вертикальных участках кривых соответствуют _{N 2} частично газообразному и частично жидкому . Тогда на кривой сосуществования есть два возможных значения Z : большее значение соответствует газу, а меньшее значение соответствует жидкости. После того, как весь газ превратился в жидкость, объем уменьшается лишь незначительно при дальнейшем увеличении давления; тогда Z почти пропорционален давлению.

По мере увеличения температуры и давления вдоль кривой сосуществования газ становится все более похожим на жидкость, а жидкость — на газ. В критической точке они одинаковы. Так, при температурах выше критической температуры (126,2 К) фазовый переход отсутствует; по мере увеличения давления газ постепенно превращается во что-то более похожее на жидкость. Чуть выше критической точки существует область давлений, в которой Z падает довольно быстро (см. кривую при 130 К), но при более высоких температурах этот процесс происходит совершенно постепенно.

На последних рисунках показано поведение при температурах, значительно превышающих критические. На отталкивающие взаимодействия температура практически не влияет, но притягивающее взаимодействие оказывает все меньшее и меньшее влияние. Таким образом, при достаточно высокой температуре отталкивающие взаимодействия доминируют при всех давлениях.

Это можно увидеть на графике, показывающем поведение при высоких температурах. По мере увеличения температуры начальный наклон становится менее отрицательным, давление, при котором Z является минимумом, становится меньше, а давление, при котором отталкивающие взаимодействия начинают доминировать, т. е. когда Z переходит от меньше единицы к большему единицы, становится меньше. При температуре Бойля (327 К для N ₂ ) эффекты притяжения и отталкивания нейтрализуют друг друга при низком давлении. Тогда Z остается на уровне идеального газа, равном единице, вплоть до давлений в несколько десятков бар. Выше температуры Бойля коэффициент сжимаемости всегда больше единицы и медленно, но неуклонно увеличивается с ростом давления.

Экспериментальные значения

Чрезвычайно трудно определить, при каких давлениях и температурах отклонение от идеального газа становится существенным. Как правило, закон идеального газа достаточно точен до давления около 2 атм и даже выше для небольших неассоциирующихся молекул. Например, для метилхлорида , молекулы с высокой полярностью и, следовательно, со значительными межмолекулярными силами, экспериментальное значение коэффициента сжимаемости равно $Z=0.9152$ при давлении 10 атм и температуре 100°С. ^[9] Для воздуха (маленьких неполярных молекул) примерно в тех же условиях коэффициент сжимаемости составляет всего $Z=1.0025$ (см. таблицу ниже для 10 бар , 400 К).

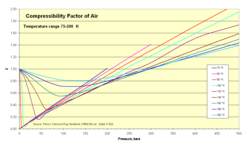
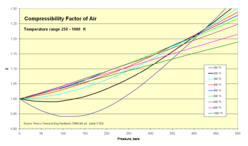
Сжимаемость воздуха

Обычный воздух в сырых количествах содержит 80 процентов азота N.
₂ и 20 процентов кислорода O
₂ . Обе молекулы малы и неполярны (и, следовательно, неассоциируются). Поэтому мы можем ожидать, что поведение воздуха в широком диапазоне температур и давлений можно с достаточной точностью аппроксимировать как идеальный газ. Экспериментальные значения коэффициента сжимаемости подтверждают это.

Z для воздуха в зависимости от давления 1–500 бар
изотермы 75–200 К
изотермы 250–1000 К

Коэффициент сжимаемости воздуха (экспериментальные значения) ^[10]
Темп. (К)	Давление абсолютное (бар)
Темп. (К)	1	5	10	20	40	60	80	100	150	200	250	300	400	500
75	0.0052	0.0260	0.0519	0.1036	0.2063	0.3082	0.4094	0.5099	0.7581	1.0125
80		0.0250	0.0499	0.0995	0.1981	0.2958	0.3927	0.4887	0.7258	0.9588	1.1931	1.4139
90	0.9764	0.0236	0.0453	0.0940	0.1866	0.2781	0.3686	0.4681	0.6779	0.8929	1.1098	1.3110	1.7161	2.1105
100	0.9797	0.8872	0.0453	0.0900	0.1782	0.2635	0.3498	0.4337	0.6386	0.8377	1.0395	1.2227	1.5937	1.9536
120	0.9880	0.9373	0.8860	0.6730	0.1778	0.2557	0.3371	0.4132	0.5964	0.7720	0.9530	1.1076	1.5091	1.7366
140	0.9927	0.9614	0.9205	0.8297	0.5856	0.3313	0.3737	0.4340	0.5909	0.7699	0.9114	1.0393	1.3202	1.5903
160	0.9951	0.9748	0.9489	0.8954	0.7803	0.6603	0.5696	0.5489	0.6340	0.7564	0.8840	1.0105	1.2585	1.4970
180	0.9967	0.9832	0.9660	0.9314	0.8625	0.7977	0.7432	0.7084	0.7180	0.7986	0.9000	1.0068	1.2232	1.4361
200	0.9978	0.9886	0.9767	0.9539	0.9100	0.8701	0.8374	0.8142	0.8061	0.8549	0.9311	1.0185	1.2054	1.3944
250	0.9992	0.9957	0.9911	0.9822	0.9671	0.9549	0.9463	0.9411	0.9450	0.9713	1.0152	1.0702	1.1990	1.3392
300	0.9999	0.9987	0.9974	0.9950	0.9917	0.9901	0.9903	0.9930	1.0074	1.0326	1.0669	1.1089	1.2073	1.3163
350	1.0000	1.0002	1.0004	1.0014	1.0038	1.0075	1.0121	1.0183	1.0377	1.0635	1.0947	1.1303	1.2116	1.3015
400	1.0002	1.0012	1.0025	1.0046	1.0100	1.0159	1.0229	1.0312	1.0533	1.0795	1.1087	1.1411	1.2117	1.2890
450	1.0003	1.0016	1.0034	1.0063	1.0133	1.0210	1.0287	1.0374	1.0614	1.0913	1.1183	1.1463	1.2090	1.2778
500	1.0003	1.0020	1.0034	1.0074	1.0151	1.0234	1.0323	1.0410	1.0650	1.0913	1.1183	1.1463	1.2051	1.2667
600	1.0004	1.0022	1.0039	1.0081	1.0164	1.0253	1.0340	1.0434	1.0678	1.0920	1.1172	1.1427	1.1947	1.2475
800	1.0004	1.0020	1.0038	1.0077	1.0157	1.0240	1.0321	1.0408	1.0621	1.0844	1.1061	1.1283	1.1720	1.2150
1000	1.0004	1.0018	1.0037	1.0068	1.0142	1.0215	1.0290	1.0365	1.0556	1.0744	1.0948	1.1131	1.1515	1.1889

$Z$ значения рассчитываются по значениям давления, объема (или плотности) и температуры в работе Вассермана, Казавчинского и Рабиновича «Теплофизические свойства воздуха и компонентов воздуха»; Москва, Наука, 1966, и НБС-НСФ ТТ 70-50095, 1971: и Вассерман и Рабинович, "Теплофизические свойства жидкого воздуха и его компонентов", Москва, 1968, и НБС-НСФ Т. 69-55092, 1970. .

См. также

Ссылки

^ Перейти обратно: ^а ^б Свойства природных газов. Архивировано 6 февраля 2011 г. в Wayback Machine . Включает диаграмму коэффициентов сжимаемости в зависимости от пониженного давления и пониженной температуры (на последней странице PDF-документа).
^ Цукер, Роберт Д.; Библарц, Оскар (2002). Основы газовой динамики (2-е изд.). Книги Уайли. ISBN 0-471-05967-6 . страница 327
^ МакКуорри, Дональд А.; Саймон, Джон Д. (1999). Молекулярная термодинамика . Университетские научные книги. ISBN 1-891389-05-Х . стр. 55
^ ИВК Рао (1997). Химическая инженерия Термодинамика . Universities Press (Индия). ISBN 81-7371-048-1 .
^ Ценгель, Юнус А.; Болес, Майкл А. (2015). Термодинамика: инженерный подход, восьмое издание . Макгроу-Хилл Образование. ISBN 978-0-07-339817-4 . стр. 140
^ Ценгель, Юнус А.; Болес, Майкл А. (2015). Термодинамика: инженерный подход, восьмое издание . Макгроу-Хилл Образование. ISBN 978-0-07-339817-4 . стр. 139
^ Смит, Дж. М.; и др. (2005). Введение в термодинамику химической инженерии (Седьмое изд.). МакГроу Хилл. ISBN 0-07-310445-0 . страница73
^ Интернет-книга NIST по химии
^ Справочник инженеров-химиков Перри (6-е изд.). МакГроу-Хилл. 1984. ISBN 0-07-049479-7 . стр. 3-268
^ Справочник инженеров-химиков Перри (6-е изд.). МакГроу-Хилл. 1984. с. 3-162 . ISBN 0-07-049479-7 .

Внешние ссылки

Коэффициент сжимаемости (газы) Статья в Citizendium.
Реальные газы, заархивированные 27 августа 2007 г. в Wayback Machine, включают обсуждение коэффициентов сжимаемости.

[Chart-1] Перейти обратно: ^а ^б Свойства природных газов. Архивировано 6 февраля 2011 г. в Wayback Machine . Включает диаграмму коэффициентов сжимаемости в зависимости от пониженного давления и пониженной температуры (на последней странице PDF-документа).

[2] Цукер, Роберт Д.; Библарц, Оскар (2002). Основы газовой динамики (2-е изд.). Книги Уайли. ISBN 0-471-05967-6 . страница 327

[3] МакКуорри, Дональд А.; Саймон, Джон Д. (1999). Молекулярная термодинамика . Университетские научные книги. ISBN 1-891389-05-Х . стр. 55

[4] ИВК Рао (1997). Химическая инженерия Термодинамика . Universities Press (Индия). ISBN 81-7371-048-1 .

[5] Ценгель, Юнус А.; Болес, Майкл А. (2015). Термодинамика: инженерный подход, восьмое издание . Макгроу-Хилл Образование. ISBN 978-0-07-339817-4 . стр. 140

[6] Ценгель, Юнус А.; Болес, Майкл А. (2015). Термодинамика: инженерный подход, восьмое издание . Макгроу-Хилл Образование. ISBN 978-0-07-339817-4 . стр. 139

[7] Смит, Дж. М.; и др. (2005). Введение в термодинамику химической инженерии (Седьмое изд.). МакГроу Хилл. ISBN 0-07-310445-0 . страница73

[NIST-8] Интернет-книга NIST по химии

[9] Справочник инженеров-химиков Перри (6-е изд.). МакГроу-Хилл. 1984. ISBN 0-07-049479-7 . стр. 3-268

[10] Справочник инженеров-химиков Перри (6-е изд.). МакГроу-Хилл. 1984. с. 3-162 . ISBN 0-07-049479-7 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]