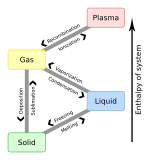
Газ

Газ – одно из четырех фундаментальных состояний материи . Остальные твердые , жидкие и плазменные . ^[1] Чистый газ может состоять из отдельных атомов (например, благородный газ, такой как неон ), элементарных молекул, состоящих из атомов одного типа (например, кислорода ), или сложных молекул, состоящих из множества атомов (например, диоксида углерода ). Газовая смесь , например воздух , содержит множество чистых газов. Что отличает газы от жидкостей и твердых тел, так это значительное разделение отдельных частиц газа . Такое разделение обычно делает бесцветный газ невидимым для человека-наблюдателя.

Газообразное состояние вещества возникает между жидким и плазменным состояниями. ^[2] последняя из которых обеспечивает верхнюю температурную границу для газов. Нижний предел температурной шкалы ограничивает вырожденные квантовые газы. ^[3] которые привлекают все большее внимание. ^[4]Атомные газы высокой плотности, переохлажденные до очень низких температур, по статистическому поведению классифицируются как бозе-газы или ферми-газы . Полный список этих экзотических состояний материи см. в списке состояний материи .

Элементарные газы

Единственными химическими элементами , которые представляют собой стабильные двухатомные гомоядерные молекулярные газы на СТП, являются водород (H ₂ ), азот (N ₂ ), кислород (O ₂ ) и два галогена : фтор (F ₂ ) и хлор (Cl ₂ ). В группе с одноатомными благородными газами — гелием (He), неоном (Ne), аргоном (Ar), криптоном (Kr), ксеноном (Xe) и радоном (Rn) — эти газы называются «элементарными газами».

Этимология

Слово газ впервые использовал фламандский химик начала 17 века Ян Баптист ван Гельмонт . ^[5] Он определил углекислый газ , первый известный газ, кроме воздуха. ^[6] Слово Ван Гельмонта, по-видимому, было просто фонетической транскрипцией древнегреческого слова χάος « хаос » – буква g в голландском языке произносится как ch в « loch » (глухой велярный фрикативный звук, / x / ) – и в этом случае Ван Гельмонт просто был следуя установившемуся алхимическому использованию, впервые засвидетельствованному в работах Парацельса . По терминологии Парацельса, хаос означал что-то вроде « сверхразреженной воды » . ^[7]

Альтернативная версия заключается в том, что термин Ван Гельмонта произошел от слова « gahst (или geist ), что означает призрак или дух». ^[8] Редакторы Оксфордского словаря английского языка не доверяют этой истории . ^[9] Напротив, франко-американский историк Жак Барсун предположил, что Ван Гельмонт заимствовал это слово из немецкого Gäscht , означающего пену, образующуюся в результате брожения . ^[10]

Физические характеристики

Поскольку большинство газов трудно наблюдать непосредственно, их описывают с помощью четырех физических свойств или макроскопических характеристик: давления , объема , количества частиц (химики группируют их по молям ) и температуры. Эти четыре характеристики неоднократно наблюдались такими учеными, как Роберт Бойль , Жак Шарль , Джон Далтон , Жозеф Гей-Люссак и Амедео Авогадро для множества газов в различных условиях. Их детальные исследования в конечном итоге привели к математической взаимосвязи между этими свойствами, выраженной законом идеального газа (см. «Идеальный и идеальный газ» § Раздел ниже).

Частицы газа сильно отделены друг от друга и, следовательно, имеют более слабые межмолекулярные связи, чем жидкости или твердые тела. Эти межмолекулярные силы возникают в результате электростатического взаимодействия между частицами газа. Одноименно заряженные области разных частиц газа отталкиваются, а противоположно заряженные области разных частиц газа притягивают друг друга; Газы, содержащие постоянно заряженные ионы , известны как плазма . Газообразные соединения с полярными ковалентными связями содержат постоянный дисбаланс зарядов и поэтому испытывают относительно сильные межмолекулярные силы, хотя суммарный заряд соединения остается нейтральным. Переходные, случайно индуцированные заряды существуют на неполярных ковалентных связях молекул, и вызываемые ими электростатические взаимодействия называются силами Ван-дер-Ваальса . Взаимодействие этих межмолекулярных сил варьируется внутри вещества, что определяет многие физические свойства, уникальные для каждого газа. ^[11]^[12] К такому выводу приводит сравнение температур кипения соединений, образованных ионной и ковалентной связью. ^[13]

По сравнению с другими состояниями вещества газы имеют низкую плотность и вязкость . Давление и температура влияют на частицы в определенном объеме. Это изменение в разделении частиц и скорости называется сжимаемостью . Такое разделение частиц и их размер влияют на оптические свойства газов, что можно найти в следующем списке показателей преломления . Наконец, частицы газа расходятся или диффундируют, чтобы равномерно распределиться по любому контейнеру.

Макроскопический взгляд на газы

При наблюдении за газом обычно указывают систему отсчета или шкалу длины . Больший масштаб длины соответствует макроскопическому или глобальному взгляду на газ. Эта область (называемая объемом) должна быть достаточной по размеру, чтобы вместить большую выборку частиц газа. Результирующий статистический анализ выборки такого размера дает «среднее» поведение (т.е. скорость, температуру или давление) всех частиц газа в данном регионе. Напротив, меньший масштаб длины соответствует микроскопической или корпускулярной точке зрения.

Макроскопически измеряемые характеристики газа измеряются либо с точки зрения самих частиц газа (скорость, давление или температура), либо с точки зрения их окружения (объем). Например, Роберт Бойль изучал пневматическую химию небольшую часть своей карьеры . Один из его экспериментов был связан с макроскопическими свойствами давления и объема газа. В его эксперименте использовался манометр с J-образной трубкой , который выглядит как пробирка в форме буквы Дж. Бойль улавливал инертный газ в закрытом конце пробирки с помощью столбика ртути , тем самым увеличивая количество частиц и температуру постоянный. Он заметил, что когда давление газа увеличивалось за счет добавления в колонну большего количества ртути, объем захваченного газа уменьшался (это известно как обратная зависимость). Более того, когда Бойль умножал давление и объем каждого наблюдения, произведение было постоянным. Это соотношение сохранялось для каждого газа, который наблюдал Бойль, что привело к закону (PV=k), названному в честь его работы в этой области.

Существует множество математических инструментов для анализа свойств газа. Поскольку газы подвергаются экстремальным условиям, эти инструменты становятся более сложными: от уравнений Эйлера для невязкого течения до уравнений Навье – Стокса. ^[14] которые полностью учитывают вязкие эффекты. Эти уравнения адаптированы к условиям рассматриваемой газовой системы. Лабораторное оборудование Бойля позволило использовать алгебру для получения аналитических результатов. Его результаты были возможны, потому что он изучал газы в условиях относительно низкого давления, где они вели себя «идеально». Эти идеальные соотношения применимы к расчетам безопасности для различных условий полета с использованием используемых материалов. Используемое сегодня высокотехнологичное оборудование было разработано, чтобы помочь нам безопасно исследовать более экзотические рабочие среды, в которых газы больше не ведут себя «идеально». Эта продвинутая математика, включающая статистику и многомерное исчисление , делает возможным решение таких сложных динамических ситуаций, как вход космического корабля в атмосферу. Примером может служить анализ изображенного на фотографии входа в атмосферу космического корабля, чтобы убедиться в том, что свойства материала в данных условиях нагрузки являются подходящими. В таком режиме полета газ ведет себя уже не идеально.

Давление

Символ, используемый для обозначения давления в уравнениях, — «p» или «P» в единицах СИ — паскалях .

При описании контейнера с газом термин «давление» (или абсолютное давление) относится к средней силе на единицу площади, которую газ оказывает на поверхность контейнера. Внутри этого объема иногда легче визуализировать частицы газа, движущиеся по прямым линиям до тех пор, пока они не столкнутся с контейнером (см. диаграмму вверху статьи). Сила, сообщаемая частицей газа контейнеру во время этого столкновения, представляет собой изменение импульса частицы. ^[15] При столкновении меняется только нормальная составляющая скорости. Частица, летящая параллельно стенке, не меняет своего импульса. Следовательно, средняя сила, действующая на поверхность, должна быть средним изменением линейного импульса от всех этих столкновений частиц газа.

Давление представляет собой сумму всех нормальных составляющих силы, оказываемой частицами, воздействующими на стенки контейнера, разделенную на площадь поверхности стенки.

Температура

Воздушный шар сжимается после погружения в жидкий азот

используется символ Для обозначения температуры в уравнениях T с единицами СИ – кельвины .

Скорость частицы газа пропорциональна ее абсолютной температуре . Объем воздушного шара на видео уменьшается, когда захваченные частицы газа замедляются с добавлением чрезвычайно холодного азота. Температура любой физической системы связана с движением частиц (молекул и атомов), составляющих [газовую] систему. ^[16] В статистической механике температура является мерой средней кинетической энергии, запасенной в молекуле (также известной как тепловая энергия). Способы хранения этой энергии диктуются степенями свободы самой молекулы ( энергетическими режимами ). Тепловая (кинетическая) энергия, добавленная к газу или жидкости ( эндотермический процесс), вызывает поступательное, вращательное и колебательное движение. Напротив, твердое тело может увеличить свою внутреннюю энергию только за счет возбуждения дополнительных колебательных мод, поскольку структура кристаллической решетки предотвращает как поступательное, так и вращательное движение. Эти нагретые молекулы газа имеют больший диапазон скоростей (более широкое распределение скоростей) с более высокой средней или средней скоростью. Разница в этом распределении обусловлена тем, что скорости отдельных частиц постоянно меняются из-за повторяющихся столкновений с другими частицами. Диапазон скоростей можно описать распределением Максвелла-Больцмана . Использование этого распределения подразумевает идеальные газы , близкие к термодинамическому равновесию для рассматриваемой системы частиц.

Удельный объем

Символ, используемый для обозначения удельного объема в уравнениях, — «v» с единицами СИ — кубическими метрами на килограмм.

Символ, используемый для обозначения объема в уравнениях, — «V» в единицах СИ — кубических метрах.

При проведении термодинамического анализа принято говорить об интенсивных и экстенсивных свойствах . Свойства, зависящие от количества газа (по массе или объёму), называются экстенсивными свойствами, а свойства, не зависящие от количества газа, — интенсивными свойствами. Удельный объем является примером интенсивного свойства, поскольку он представляет собой отношение объема, занимаемого единицей массы газа, который одинаков во всей системе, находящейся в равновесии. ^[17] 1000 атомов газа занимают то же пространство, что и любые другие 1000 атомов при любой заданной температуре и давлении. Эту концепцию легче визуализировать для твердых тел, таких как железо, которые несжимаемы по сравнению с газами. Однако объем сам по себе, а не конкретный, является обширным свойством.

Плотность

Символ, используемый для обозначения плотности в уравнениях, — ρ (rho) с единицами СИ — килограммами на кубический метр. Этот член является обратной величиной удельного объема.

Поскольку молекулы газа могут свободно перемещаться внутри контейнера, их масса обычно характеризуется плотностью. Плотность — это количество массы на единицу объема вещества, или величина, обратная удельному объему. Плотность газов может варьироваться в широком диапазоне, поскольку частицы могут свободно перемещаться ближе друг к другу, когда их ограничивает давление или объем. Это изменение плотности называется сжимаемостью . Подобно давлению и температуре, плотность является переменной состояния газа, и изменение плотности во время любого процесса регулируется законами термодинамики. одинакова Плотность статического газа по всему объему сосуда. Следовательно, плотность является скалярной величиной . С помощью кинетической теории можно показать, что плотность обратно пропорциональна размеру контейнера, в котором заключена фиксированная масса газа. В случае фиксированной массы плотность уменьшается с увеличением объема.

Микроскопический вид газов

Если бы можно было наблюдать газ под мощным микроскопом, то можно было бы увидеть совокупность частиц без какой-либо определенной формы и объема, находящихся в более или менее хаотическом движении. Эти частицы газа меняют направление только тогда, когда они сталкиваются с другой частицей или со стенками контейнера. Этот микроскопический взгляд на газ хорошо описан статистической механикой , но его можно описать множеством различных теорий. Кинетическая теория газов , предполагающая, что эти столкновения совершенно упругие , не учитывает межмолекулярные силы притяжения и отталкивания.

Кинетическая теория газов

Кинетическая теория дает представление о макроскопических свойствах газов, рассматривая их молекулярный состав и движение. Начнем с определений импульса и кинетической энергии . ^[18] можно использовать сохранение импульса и геометрические соотношения куба, чтобы связать свойства макроскопической системы температуры и давления с микроскопическими свойствами кинетической энергии на молекулу. Теория дает усредненные значения этих двух свойств.

Кинетическая теория газов может помочь объяснить, как система (рассматриваемая совокупность частиц газа) реагирует на изменения температуры с соответствующим изменением кинетической энергии .

Например: представьте, что у вас есть герметичный контейнер фиксированного размера ( постоянного объема), содержащий фиксированное количество частиц газа; начиная с абсолютного нуля (теоретической температуры, при которой атомы или молекулы не имеют тепловой энергии, т.е. не движутся и не вибрируют), вы начинаете добавлять энергию в систему, нагревая контейнер, так что энергия передается частицам внутри. Как только их внутренняя энергия превысит нулевую энергию , то есть их кинетическая энергия (также известная как тепловая энергия ) станет отличной от нуля, частицы газа начнут перемещаться вокруг контейнера. По мере дальнейшего нагрева ящика (по мере добавления большего количества энергии) средняя скорость отдельных частиц увеличивается по мере увеличения общей внутренней энергии системы. Более высокая средняя скорость всех частиц приводит к большей ( т.е. частоте столкновений большему количеству столкновений в единицу времени) между частицами и контейнером, а также между самими частицами.

Макроскопическая . , измеримая величина давления является прямым результатом этих столкновений микроскопических частиц с поверхностью, над которой отдельные молекулы оказывают небольшое воздействие, каждая из которых вносит свой вклад в общую силу, приложенную в пределах определенной области ( Прочитайте « Давление » в приведенном выше разделе « Макроскопический взгляд на газы ».)

Точно так же макроскопически измеримая величина температуры представляет собой количественную оценку общего количества движения или кинетической энергии, которую проявляют частицы. ( Прочтите « Температура » в предыдущем разделе « Макроскопический взгляд на газы ».)

Тепловое движение и статистическая механика

В кинетической теории газов предполагается, что кинетическая энергия состоит исключительно из линейных перемещений в соответствии с скоростей частиц распределением в системе. Однако в реальных газах и других реальных веществах движения, определяющие кинетическую энергию системы (которые в совокупности определяют температуру), гораздо сложнее, чем простое линейное перемещение , из-за более сложной структуры молекул по сравнению с отдельными атомами, которые действуют аналогично точечным массам . В реальных термодинамических системах большую роль в определении тепловых движений играют квантовые явления. Случайные тепловые движения (кинетическая энергия) в молекулах представляют собой комбинацию конечного набора возможных движений, включая перемещение, вращение и вибрацию . Этот конечный диапазон возможных движений вместе с конечным набором молекул в системе приводит к конечному числу микросостояний внутри системы; совокупность всех микросостояний мы называем ансамблем . В зависимости от ситуации, в зависимости от ситуации, в зависимости от ситуации мы потенциально можем иметь три различных типа ансамблей: микроканонический ансамбль , канонический ансамбль или великий канонический ансамбль . Конкретные комбинации микросостояний внутри ансамбля — это то, как мы действительно определяем макросостояние системы (температура, давление, энергия и т. д.). Для этого мы должны сначала посчитать все микросостояния с помощью функции статистического распределения . Использование статистической механики и статистической суммы является важным инструментом во всей физической химии, поскольку это ключ к связи между микроскопическими состояниями системы и макроскопическими переменными, которые мы можем измерить, такими как температура, давление, теплоемкость. , внутренняя энергия, энтальпия и энтропия, и это лишь некоторые из них. ( Читайте : Функция раздела Значение и значение )

Использование статистической суммы для определения энергии молекулы или системы молекул иногда можно аппроксимировать теоремой о равнораспределении , что значительно упрощает расчет. Однако этот метод предполагает, что все степени свободы молекулы одинаково заселены и, следовательно, одинаково используются для хранения энергии внутри молекулы. Это означало бы, что внутренняя энергия изменяется линейно с температурой, но это не так. При этом игнорируется тот факт, что теплоемкость меняется с температурой, поскольку определенные степени свободы недостижимы (так называемые «замороженные») при более низких температурах. По мере увеличения внутренней энергии молекул растет и способность хранить энергию в пределах дополнительных степеней свободы. Поскольку для удержания энергии становится доступно больше степеней свободы, это приводит к увеличению молярной теплоемкости вещества. ^[19]

Броуновское движение

Броуновское движение — это математическая модель, используемая для описания случайного движения частиц, взвешенных в жидкости. Анимация частиц газа с использованием розовых и зеленых частиц иллюстрирует, как такое поведение приводит к распространению газов ( энтропия ). Эти события также описываются теорией частиц .

Поскольку наблюдение за отдельными частицами газа (атомами или молекулами) находится на пределе (или за пределами) современных технологий, только теоретические расчеты дают предположения о том, как они движутся, но их движение отличается от броуновского движения, поскольку броуновское движение включает в себя плавное сопротивление из-за к силе трения многих молекул газа, перемежающейся сильными столкновениями отдельной (или нескольких) молекул газа с частицей. Таким образом, частица (обычно состоящая из миллионов или миллиардов атомов) движется неровно, но не так неровно, как можно было бы ожидать, если бы рассматривалась отдельная молекула газа.

Межмолекулярные силы – основное различие между реальными и идеальными газами

Силы между двумя или более молекулами или атомами, притягивающие или отталкивающие, называются межмолекулярными силами . Межмолекулярные силы испытывают молекулы, когда они находятся в физической близости друг от друга. ^[20]^[21] Эти силы очень важны для правильного моделирования молекулярных систем, поскольку позволяют точно предсказать микроскопическое поведение молекул в любой системе, и, следовательно, необходимы для точного прогнозирования физических свойств газов (и жидкостей) в широких пределах физических условий.

В результате изучения физической химии одной из самых известных межмолекулярных сил в физике являются силы Ван-дер-Ваальса . Силы Ван-дер-Ваальса играют ключевую роль в определении почти всех физических свойств жидкостей, таких как вязкость , скорость потока и газодинамика (см. раздел «Физические характеристики»). Взаимодействия Ван-дер-Ваальса между молекулами газа являются причиной того, что моделирование «реального газа» математически сложнее, чем « идеального газа». Игнорирование этих сил, зависящих от близости, позволяет реальный газ рассматривать как идеальный газ , что значительно упрощает расчеты.

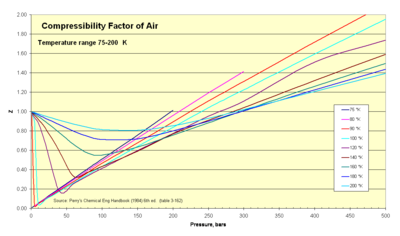
Межмолекулярное притяжение и отталкивание между двумя молекулами газа зависят от расстояния между ними. Комбинация притяжения и отталкивания хорошо моделируется потенциалом Леннарда-Джонса . ^[22]^[23] который является одним из наиболее широко изученных из всех межатомных потенциалов, описывающих потенциальную энергию молекулярных систем. Из-за общей применимости и важности модельную систему Леннарда-Джонса часто называют «Леннардом-Джонсиумом». ^[24]^[25] Потенциал Леннарда-Джонса между молекулами можно разбить на две отдельные составляющие: дальнее притяжение, обусловленное дисперсионной силой Лондона , и ближнедействующее отталкивание, обусловленное электрон-электронным обменным взаимодействием (что связано с принципом запрета Паули). ).

Когда две молекулы находятся на относительном расстоянии (это означает, что они имеют высокую потенциальную энергию), на них действует слабая сила притяжения, заставляющая их двигаться навстречу друг другу, снижая их потенциальную энергию. Однако если молекулы находятся слишком далеко , они не будут испытывать какой-либо значимой силы притяжения. Кроме того, если молекулы подойдут слишком близко , они столкнутся и испытают очень высокую силу отталкивания (моделируемую твердыми сферами ), которая намного сильнее силы притяжения, поэтому любое притяжение, вызванное близостью, игнорируется.

Когда две молекулы приближаются друг к другу на расстоянии, которое не является ни слишком большим, ни слишком близким, их притяжение увеличивается по мере увеличения величины их потенциальной энергии (становясь более отрицательной) и снижает их общую внутреннюю энергию. ^[26] Притяжение, заставляющее молекулы сближаться, может произойти только в том случае, если молекулы остаются рядом в течение времени, необходимого для физического сближения . Следовательно, силы притяжения наиболее сильны, когда молекулы движутся с низкой скоростью . Это означает, что притяжение между молекулами существенно температурах газа при низких . Однако если вам придется изотермически сжимать этот холодный газ в небольшой объем, сближая молекулы и повышая давление, отталкивания начнут доминировать над притяжениями, поскольку скорость столкновений значительно увеличится. Следовательно, при низких температурах и низких давлениях притяжение преобладающим межмолекулярным взаимодействием является .

Если две молекулы движутся с высокими скоростями в произвольных направлениях по непересекающимся путям, то они не проведут достаточно времени рядом, чтобы на них воздействовала сила притяжения лондонской дисперсии. Если две молекулы столкнутся, они будут двигаться слишком быстро, и их кинетическая энергия будет намного больше, чем любая потенциальная энергия притяжения, поэтому при столкновении они испытают отталкивание. можно пренебречь Таким образом, притяжением между молекулами при высоких температурах из-за больших скоростей . При высоких температурах и высоких давлениях отталкивание преобладающим межмолекулярным взаимодействием является .

С учетом вышеизложенных эффектов, вызывающих эти притяжения и отталкивания, реальные газы отличаются от модели идеального газа следующим обобщением: ^[27]

При низких температурах и низких давлениях объем, занимаемый реальным газом, меньше объема, предсказываемого законом идеального газа.
При высоких температурах и высоких давлениях объем, занимаемый реальным газом, превышает объем, предсказываемый законом идеального газа.

Математические модели

Уравнение состояния (для газов) — это математическая модель, используемая для грубого описания или прогнозирования свойств состояния газа. В настоящее время не существует единого уравнения состояния, которое бы точно предсказывало свойства всех газов при любых условиях. Поэтому для газов в определенных диапазонах температур и давлений был разработан ряд гораздо более точных уравнений состояния. Наиболее широко обсуждаются «газовые модели»: «идеальный газ», «идеальный газ» и «реальный газ». Каждая из этих моделей имеет свой набор допущений, облегчающих анализ данной термодинамической системы. ^[28] Каждая последующая модель расширяет температурный диапазон покрытия, к которому она применима.

Идеальный и совершенный газ

Уравнение состояния идеального или совершенного газа представляет собой закон идеального газа и гласит:

PV=nRT,

где P — давление, V — объем, n — количество газа (в мольных единицах), R — универсальная газовая постоянная , 8,314 Дж/(моль К), а T — температура. Написанную таким образом, ее иногда называют «химической версией», поскольку в ней подчеркивается число молекул n . Это также можно записать как

P=\rho R_{s}T,

где $R_{s}$ — удельная газовая постоянная для конкретного газа в единицах Дж/(кг-К), а ρ = м/В — плотность. Это обозначение представляет собой версию «газодинамики», которая более практична при моделировании газовых потоков с ускорением без химических реакций.

Закон идеального газа не делает предположений об удельной теплоёмкости газа. В самом общем случае теплоемкость является функцией температуры и давления. Если в конкретном приложении пренебрегают зависимостью от давления (а, возможно, и температурной зависимостью), иногда газ называют идеальным газом , хотя точные предположения могут варьироваться в зависимости от автора и/или области науки.

Для идеального газа закон идеального газа применяется без ограничений на теплоемкость. Идеальный газ — это упрощенный «реальный газ» в предположении, что коэффициент сжимаемости Z установлен равным 1, что означает, что это пневматическое соотношение остается постоянным. Коэффициент сжимаемости, равный единице, также требует, чтобы четыре переменные состояния подчинялись закону идеального газа .

Это приближение больше подходит для приложений в технике, хотя можно использовать более простые модели для получения примерного диапазона того, где должно находиться реальное решение. Примером, где подойдет «приближение идеального газа», может служить камера сгорания реактивного двигателя . ^[29] Также может быть полезно сохранить элементарные реакции и химическую диссоциацию для расчета выбросов .

настоящий газ

21 апреля 1990 г. извержение горы Редут на Аляске, иллюстрирующее существование реальных газов, не находящихся в термодинамическом равновесии.

Каждое из перечисленных ниже предположений усложняет решение проблемы. Поскольку плотность газа увеличивается с ростом давления, межмолекулярные силы играют более существенную роль в поведении газа, в результате чего закон идеального газа больше не дает «разумных» результатов. В верхней части температурного диапазона двигателя (например, секции камеры сгорания – 1300 К) сложные частицы топлива поглощают внутреннюю энергию посредством вращения и вибрации, что приводит к тому, что их удельная теплота отличается от теплоемкости двухатомных молекул и благородных газов. При более чем вдвое большей температуре начинают происходить электронное возбуждение и диссоциация частиц газа, заставляя давление приспосабливаться к большему числу частиц (переход от газа к плазме ). ^[30] Наконец, предполагалось, что все термодинамические процессы описывают однородные газы, скорости которых изменяются согласно фиксированному распределению. Использование неравновесной ситуации подразумевает, что поле потока должно быть каким-то образом охарактеризовано, чтобы обеспечить решение. Одной из первых попыток расширить границы закона идеального газа было включение в него различных термодинамических процессов путем корректировки уравнения для чтения pV. ^н = константа , а затем варьируя n через различные значения, такие как коэффициент удельной теплоемкости γ .

Реальные эффекты газа включают корректировки, внесенные для учета более широкого диапазона поведения газа:

Эффекты сжимаемости ( Z допускается варьировать от 1,0)
Переменная теплоемкость (удельная теплоемкость меняется в зависимости от температуры)
Силы Ван дер Ваальса (связанные со сжимаемостью, могут заменять другие уравнения состояния)
Неравновесные термодинамические эффекты
Вопросы молекулярной диссоциации и элементарных реакций переменного состава.

Для большинства приложений такой детальный анализ является излишним. Примерами того, где реальные эффекты газа могли бы оказать существенное влияние, могут служить в атмосферу космического корабля "Шаттл" вход , где присутствовали чрезвычайно высокие температуры и давления, или газы, образующиеся во время геологических событий, как на примере извержения горы Редут в 1990 году .

Постоянный газ

Постоянный газ — это термин, используемый для газа, критическая температура которого ниже диапазона обычных температур, пригодных для проживания человека, и поэтому не может быть сжижена под давлением в этом диапазоне. Исторически считалось, что такие газы невозможно сжижать, и поэтому они постоянно остаются в газообразном состоянии. Этот термин относится к хранению при температуре окружающей среды и транспортировке газов под высоким давлением. ^[31]

Исторические исследования

Закон Бойля

Закон Бойля был, пожалуй, первым выражением уравнения состояния. В 1662 году Роберт Бойль провел серию экспериментов с J-образной стеклянной трубкой, запаянной с одного конца. В трубку добавляли ртуть, удерживая фиксированное количество воздуха в коротком запечатанном конце трубки. Затем объем газа тщательно измеряли по мере добавления в трубку дополнительной ртути. Давление газа можно было определить по разнице между уровнем ртути в коротком конце трубки и в длинном открытом конце. На изображении оборудования Бойля показаны некоторые экзотические инструменты, которые Бойль использовал во время изучения газов.

В ходе этих экспериментов Бойль заметил, что давление, оказываемое газом при постоянной температуре, изменяется обратно пропорционально объему газа. ^[32] Например, если объем уменьшить вдвое, давление увеличится вдвое; а если объем увеличить вдвое, давление уменьшится вдвое. Учитывая обратную зависимость между давлением и объемом, произведение давления ( P ) и объема ( V ) является константой ( k ) для данной массы замкнутого газа, пока температура постоянна. В виде формулы это выглядит следующим образом:

PV=k

Поскольку объемы и давления фиксированного количества газа до и после, где температуры до и после одинаковы, оба равны константе k , их можно связать уравнением:

$\qquad P_{1}V_{1}=P_{2}V_{2}.$

Закон Чарльза

В 1787 году французский физик и пионер воздушных шаров Жак Шарль обнаружил, что кислород, азот, водород, углекислый газ и воздух расширяются в одинаковой степени в одном и том же интервале 80 Кельвинов. Он заметил, что для идеального газа при постоянном давлении объем прямо пропорционален его температуре:

{\frac {V_{1}}{T_{1}}}={\frac {V_{2}}{T_{2}}}

Закон Гей-Люссака

В 1802 году Жозеф Луи Гей-Люссак опубликовал результаты аналогичных, хотя и более обширных экспериментов. ^[33] Гей-Люссак отдал должное более ранней работе Шарля, назвав закон в его честь. Самому Гей-Люссаку приписывают закон описания давления, который он нашел в 1809 году. Он гласит, что давление, оказываемое на стенки сосуда идеальным газом, пропорционально его температуре.

{\frac {P_{1}}{T_{1}}}={\frac {P_{2}}{T_{2}}}\,

Закон Авогадро

В 1811 году Амедео Авогадро доказал, что равные объёмы чистых газов содержат одинаковое количество частиц. Его теория не была общепринятой до 1858 года, когда другой итальянский химик Станислао Канниццаро смог объяснить неидеальные исключения. В его работе с газами, проведенной столетием ранее, физическая константа, носящая его имя ( константа Авогадро ), представляет собой число атомов на моль элементарного углерода-12 ( 6,022 × 10). ²³ моль ⁻¹). Это конкретное количество частиц газа при стандартных температуре и давлении (закон идеального газа) занимает 22,40 литра, что называется молярным объемом .

Закон Авогадро гласит, что объем, занимаемый идеальным газом, пропорционален количеству вещества в этом объеме. Это приводит к молярному объему газа, который при СТП составляет 22,4 дм3. ³/моль (литры на моль). Отношение определяется выражением ${\frac {V_{1}}{n_{1}}}={\frac {V_{2}}{n_{2}}},$ где n — количество вещества газа (число молекул, делённое на константу Авогадро ).

Закон Дальтона

В 1801 году Джон Дальтон опубликовал закон парциального давления из своей работы с соотношением закона идеального газа: Давление смеси нереакционноспособных газов равно сумме давлений всех составляющих газов по отдельности. Математически это можно представить для n видов как:

давление _Общее = Давление ₁ + Давление ₂ + ... + Давление _n

На изображении дневника Далтона изображена символика, которую он использовал для обозначения пути, по которому он следовал. Среди его ключевых журнальных наблюдений по смешиванию нереакционноспособных «упругих жидкостей» (газов) были следующие: ^[34]

В отличие от жидкостей, более тяжелые газы при смешивании не оседали на дно.
Идентичность частиц газа не играла роли в определении конечного давления (они вели себя так, как будто их размер был пренебрежимо мал).

Специальные темы

Сжимаемость

Термодинамики используют этот коэффициент ( Z ), чтобы изменить уравнение идеального газа, чтобы учесть эффекты сжимаемости реальных газов. Этот коэффициент представляет собой соотношение фактических и идеальных удельных объемов. Его иногда называют «фактором выдумки» или поправкой, позволяющей расширить полезный диапазон закона идеального газа для целей проектирования. Обычно это значение Z очень близко к единице. Изображение коэффициента сжимаемости показывает, как Z изменяется в диапазоне очень низких температур.

Число Рейнольдса

механике жидкости число Рейнольдса — это отношение сил инерции ( vsρ _В ) к силам вязкости ( μ/L ). Это одно из наиболее важных безразмерных чисел в гидродинамике, которое обычно используется вместе с другими безразмерными числами в качестве критерия для определения динамического подобия. Таким образом, число Рейнольдса обеспечивает связь между результатами моделирования (проектированием) и полномасштабными фактическими условиями. Его также можно использовать для характеристики потока.

Вязкость

Спутниковый снимок погодных условий в окрестностях островов Робинзона Крузо 15 сентября 1999 года показывает турбулентный узор облаков, называемый вихревой улицей Кармана.

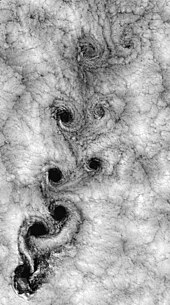
Вязкость, физическое свойство, является мерой того, насколько хорошо соседние молекулы прилипают друг к другу. Твердое тело может выдерживать силу сдвига благодаря силе этих липких межмолекулярных сил. Жидкость будет постоянно деформироваться под воздействием одинаковой нагрузки. Хотя газ имеет более низкое значение вязкости, чем жидкость, это все же наблюдаемое свойство. Если бы газы не имели вязкости, то они не прилипали бы к поверхности крыла и не образовывали бы пограничный слой. Исследование дельта -крыла на шлирен -изображении показывает, что частицы газа прилипают друг к другу (см. раздел «Пограничный слой»).

Турбулентность

В гидродинамике турбулентность или турбулентный поток — это режим течения, характеризующийся хаотическими, стохастическими изменениями свойств. Сюда входит диффузия с низким импульсом, конвекция с высоким импульсом и быстрое изменение давления и скорости в пространстве и времени. Спутниковый снимок погоды вокруг островов Робинзона Крузо иллюстрирует один из примеров.

Пограничный слой

Частицы, по сути, «прилипают» к поверхности проходящего через нее объекта. Этот слой частиц называется пограничным слоем. На поверхности объекта он по существу статичен из-за трения поверхности. Объект с его пограничным слоем фактически представляет собой новую форму объекта, которую остальные молекулы «видят» по мере приближения объекта. Этот пограничный слой может отделиться от поверхности, по существу создавая новую поверхность и полностью изменяя путь потока. Классическим примером этого является сваливающийся профиль крыла . На изображении треугольного крыла отчетливо видно утолщение пограничного слоя по мере течения газа справа налево вдоль передней кромки.

Принцип максимальной энтропии

Поскольку общее число степеней свободы приближается к бесконечности, система будет находиться в макросостоянии , соответствующем наибольшей кратности . Чтобы проиллюстрировать этот принцип, измерьте температуру кожи замороженного металлического стержня. Используя тепловое изображение температуры кожи, обратите внимание на распределение температуры на поверхности. Это первоначальное наблюдение температуры представляет собой « микросостояние ». Когда-нибудь в будущем второе наблюдение температуры кожи создаст второе микросостояние. Продолжая этот процесс наблюдения, можно создать серию микросостояний, которые иллюстрируют тепловую историю поверхности стержня. Охарактеризовать эту историческую серию микрогосударств можно, выбрав макрогосударство, которое успешно классифицирует их все в единую группу.

Термодинамическое равновесие

Когда передача энергии прекращается из системы, это состояние называется термодинамическим равновесием. Обычно это условие подразумевает, что система и окружающая среда имеют одинаковую температуру, поэтому тепло между ними больше не передается. Это также означает, что внешние силы уравновешены (объем не меняется) и все химические реакции внутри системы завершены. Сроки этих событий различаются в зависимости от рассматриваемой системы. Контейнер со льдом, которому разрешено плавиться при комнатной температуре, занимает несколько часов, в то время как в полупроводниках передача тепла, происходящая при переходе устройства из включенного состояния в выключенное, может составлять порядка нескольких наносекунд.

Фазовые переходы вещества (
v
т
и
)
К От	Твердый	Жидкость	Газ	Плазма
Твердый		плавление	Сублимация
Жидкость	Замораживание		Испарение
Газ	Депонирование	Конденсат		Ионизация
Плазма			Рекомбинация

См. также

Примечания

^ «Газ» . Мерриам-Вебстер . 7 августа 2023 г.
^ Это обсуждение начала 20-го века делает вывод о том, что считается состоянием плазмы. См. стр. 137 журнала Американского химического общества, Общества Фарадея, Химического общества (Великобритания), Журнал физической химии, том 11, Корнелл (1907).
^ Зелевинский, Таня (9 ноября 2009 г.). «…как раз для образования бозе-эйнштейновского конденсата» . Физика . 2 (20): 94. arXiv : 0910.0634 . doi : 10.1103/PhysRevLett.103.200401 . ПМИД 20365964 . S2CID 14321276 .
^ «Квантовый газовый микроскоп позволяет увидеть необычные ультрахолодные атомы» . ScienceDaily . Проверено 06 февраля 2023 г.
^ Гельмонт, Ян Баптист Ван (1652). Рождение медицины, то есть начало неслыханной физики... автора Джоан Баптиста Ван Гельмонт,... (на латыни). у Л. Эльзевириуса. Слово «газ» впервые появляется на стр. 58 , где он упоминает: «...Gas (meum scil. inventum)...» (...газ (именно мое открытие)...). На странице 59 он заявляет: «... нуждаясь в названии, я назвал это дыхание Газом, недалеко от Чао...» (... нуждаясь в названии, я назвал этот пар «газом», а не далеко не "хаос"...)
^ Лей, Вилли (июнь 1966 г.). «Перепроектированная Солнечная система» . Довожу до вашего сведения. Галактическая научная фантастика . стр. 94–106.
^ Харпер, Дуглас. «газ» . Интернет-словарь этимологии .
^ Дрейпер, Джон Уильям (1861). Учебник по химии . Нью-Йорк: Харпер и сыновья. п. 178.
^ " "газ, н.1 и прил." ". ОЭД онлайн . Издательство Оксфордского университета. Июнь 2021 года. Вероятно, нет никаких оснований в идее (начиная с XVIII века и далее, например, в J. Priestley On Air (1774), Introd. 3) о том, что ван Гельмонт смоделировал газ на основе голландского духа Geest или любого из его родственников.
^ Барсун, Жак (2000). От рассвета до упадка: 500 лет западной культурной жизни . Нью-Йорк: Издательство HarperCollins. п. 199.
^ Авторы устанавливают связь между молекулярными силами металлов и соответствующими им физическими свойствами. В более широком смысле эта концепция применима и к газам, хотя и не повсеместно. Корнелл (1907), стр. 164–5.
^ Одним заметным исключением из этой связи физических свойств является проводимость, которая варьируется в зависимости от состояния вещества (ионных соединений в воде), как описано Майклом Фарадеем в 1833 году, когда он заметил, что лед не проводит ток. См. стр. 45 книги Джона Тиндаля «Фарадей как первооткрыватель» (1868 г.).
^ Джон С. Хатчинсон (2008). Разработка концепции исследований в области химии . п. 67.
^ Андерсон, стр.501
^ Дж. Клерк Максвелл (1904). Теория тепла . Минеола: Dover Publications. стр. 319–20. ISBN 978-0-486-41735-6 .
^ См. страницы 137–8 Общества, Корнелл (1907).
^ Кеннет Уорк (1977). Термодинамика (3-е изд.). МакГроу-Хилл. п. 12 . ISBN 978-0-07-068280-1 .
^ Предположения кинетической теории см. в McPherson, стр. 60–61.
^ Йешке, Гуннар (26 ноября 2020 г.). «Канонический ансамбль» . Архивировано из оригинала 20 мая 2021 г.
^ Фишер, Иоганн; Вендланд, Мартин (октябрь 2023 г.). «К истории ключевых эмпирических межмолекулярных потенциалов» . Жидкостно-фазовые равновесия . 573 : 113876. Бибкод : 2023FlPEq.57313876F . дои : 10.1016/j.fluid.2023.113876 .
^ «Межмолекулярные и поверхностные силы» , Межмолекулярные и поверхностные силы , Elsevier, 2011, стр. iii, doi : 10.1016/b978-0-12-391927-4.10024-6 , ISBN 978-0-12-391927-4 , получено 1 июля 2024 г.
^ Ленхард, Йоханнес; Стефан, Саймон; Хассе, Ганс (июнь 2024 г.). «К истории потенциала Леннарда-Джонса» . Аннален дер Физик . 536 (6). дои : 10.1002/andp.202400115 . ISSN 0003-3804 .
^ Джонс, Дж. Э. (октябрь 1924 г.). «К определению молекулярных полей. — II. Из уравнения состояния газа» . Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера . 106 (738): 463–477. Бибкод : 1924RSPSA.106..463J . дои : 10.1098/rspa.1924.0082 . ISSN 0950-1207 .
^ Ленхард, Йоханнес; Стефан, Саймон; Хассе, Ганс (февраль 2024 г.). «Дитя предсказания. Об истории, онтологии и вычислениях Леннарда-Джонезиума» . Исследования по истории и философии науки . 103 : 105–113. дои : 10.1016/j.shpsa.2023.11.007 . ПМИД 38128443 .
^ Стефан, Саймон; Тол, Моника; Врабец, Ядран; Хассе, Ганс (28 октября 2019 г.). «Теплофизические свойства жидкости Леннарда-Джонса: база данных и оценка данных» . Журнал химической информации и моделирования . 59 (10): 4248–4265. doi : 10.1021/acs.jcim.9b00620 . ISSN 1549-9596 . ПМИД 31609113 .
^ «Потенциал Леннарда-Джонса — LibreTexts по химии» . 22 августа 2020 г. Архивировано из оригинала 22 августа 2020 г. Проверено 20 мая 2021 г.
^ «14.11: Реальные и идеальные газы — LibreTexts по химии» . 06.02.2021. Архивировано из оригинала 06 февраля 2021 г. Проверено 20 мая 2021 г.
^ Андерсон, стр. 289–291.
^ Джон, стр.205
^ Джон, стр. 247–56.
^ «Постоянный газ» . www.oxfordreference.com . Издательство Оксфордского университета . Проверено 3 апреля 2021 г.
^ Макферсон, стр. 52–55.
^ Макферсон, стр. 55–60.
^ Джон П. Миллингтон (1906). Джон Далтон . стр. 72, 77–78.

Ссылки

Андерсон, Джон Д. (1984). Основы аэродинамики . Высшее образование МакГроу-Хилл. ISBN 978-0-07-001656-9 .
Джон, Джеймс (1984). Газодинамика . Аллин и Бэкон. ISBN 978-0-205-08014-4 .
Макферсон, Уильям; Хендерсон, Уильям (1917). Элементарное изучение химии .

Дальнейшее чтение

Филип Хилл и Карл Петерсон. Механика и термодинамика движения: второе издание Аддисон-Уэсли, 1992. ISBN 0-201-14659-2
Национальное управление по аэронавтике и исследованию космического пространства (НАСА). Анимированная газовая лаборатория . По состоянию на февраль 2008 г.
Государственный университет Джорджии. Гиперфизика . По состоянию на февраль 2008 г.
Энтони Льюис WordWeb . По состоянию на февраль 2008 г.
Колледж Северо-Западного Мичигана Газообразный штат . По состоянию на февраль 2008 г.
Льюис, Вивиан Байам; Лунге, Георг (1911). «Газ» . Британская энциклопедия . Том. 11 (11-е изд.). п. 481–493.

[1] «Газ» . Мерриам-Вебстер . 7 августа 2023 г.

[2] Это обсуждение начала 20-го века делает вывод о том, что считается состоянием плазмы. См. стр. 137 журнала Американского химического общества, Общества Фарадея, Химического общества (Великобритания), Журнал физической химии, том 11, Корнелл (1907).

[3] Зелевинский, Таня (9 ноября 2009 г.). «…как раз для образования бозе-эйнштейновского конденсата» . Физика . 2 (20): 94. arXiv : 0910.0634 . doi : 10.1103/PhysRevLett.103.200401 . ПМИД 20365964 . S2CID 14321276 .

[4] «Квантовый газовый микроскоп позволяет увидеть необычные ультрахолодные атомы» . ScienceDaily . Проверено 06 февраля 2023 г.

[5] Гельмонт, Ян Баптист Ван (1652). Рождение медицины, то есть начало неслыханной физики... автора Джоан Баптиста Ван Гельмонт,... (на латыни). у Л. Эльзевириуса. Слово «газ» впервые появляется на стр. 58 , где он упоминает: «...Gas (meum scil. inventum)...» (...газ (именно мое открытие)...). На странице 59 он заявляет: «... нуждаясь в названии, я назвал это дыхание Газом, недалеко от Чао...» (... нуждаясь в названии, я назвал этот пар «газом», а не далеко не "хаос"...)

[ley196606-6] Лей, Вилли (июнь 1966 г.). «Перепроектированная Солнечная система» . Довожу до вашего сведения. Галактическая научная фантастика . стр. 94–106.

[et-7] Харпер, Дуглас. «газ» . Интернет-словарь этимологии .

[8] Дрейпер, Джон Уильям (1861). Учебник по химии . Нью-Йорк: Харпер и сыновья. п. 178.

[9] " "газ, н.1 и прил." ". ОЭД онлайн . Издательство Оксфордского университета. Июнь 2021 года. Вероятно, нет никаких оснований в идее (начиная с XVIII века и далее, например, в J. Priestley On Air (1774), Introd. 3) о том, что ван Гельмонт смоделировал газ на основе голландского духа Geest или любого из его родственников.

[10] Барсун, Жак (2000). От рассвета до упадка: 500 лет западной культурной жизни . Нью-Йорк: Издательство HarperCollins. п. 199.

[11] Авторы устанавливают связь между молекулярными силами металлов и соответствующими им физическими свойствами. В более широком смысле эта концепция применима и к газам, хотя и не повсеместно. Корнелл (1907), стр. 164–5.

[12] Одним заметным исключением из этой связи физических свойств является проводимость, которая варьируется в зависимости от состояния вещества (ионных соединений в воде), как описано Майклом Фарадеем в 1833 году, когда он заметил, что лед не проводит ток. См. стр. 45 книги Джона Тиндаля «Фарадей как первооткрыватель» (1868 г.).

[13] Джон С. Хатчинсон (2008). Разработка концепции исследований в области химии . п. 67.

[14] Андерсон, стр.501

[15] Дж. Клерк Максвелл (1904). Теория тепла . Минеола: Dover Publications. стр. 319–20. ISBN 978-0-486-41735-6 .

[16] См. страницы 137–8 Общества, Корнелл (1907).

[17] Кеннет Уорк (1977). Термодинамика (3-е изд.). МакГроу-Хилл. п. 12 . ISBN 978-0-07-068280-1 .

[18] Предположения кинетической теории см. в McPherson, стр. 60–61.

[19] Йешке, Гуннар (26 ноября 2020 г.). «Канонический ансамбль» . Архивировано из оригинала 20 мая 2021 г.

[20] Фишер, Иоганн; Вендланд, Мартин (октябрь 2023 г.). «К истории ключевых эмпирических межмолекулярных потенциалов» . Жидкостно-фазовые равновесия . 573 : 113876. Бибкод : 2023FlPEq.57313876F . дои : 10.1016/j.fluid.2023.113876 .

[21] «Межмолекулярные и поверхностные силы» , Межмолекулярные и поверхностные силы , Elsevier, 2011, стр. iii, doi : 10.1016/b978-0-12-391927-4.10024-6 , ISBN 978-0-12-391927-4 , получено 1 июля 2024 г.

[22] Ленхард, Йоханнес; Стефан, Саймон; Хассе, Ганс (июнь 2024 г.). «К истории потенциала Леннарда-Джонса» . Аннален дер Физик . 536 (6). дои : 10.1002/andp.202400115 . ISSN 0003-3804 .

[23] Джонс, Дж. Э. (октябрь 1924 г.). «К определению молекулярных полей. — II. Из уравнения состояния газа» . Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера . 106 (738): 463–477. Бибкод : 1924RSPSA.106..463J . дои : 10.1098/rspa.1924.0082 . ISSN 0950-1207 .

[24] Ленхард, Йоханнес; Стефан, Саймон; Хассе, Ганс (февраль 2024 г.). «Дитя предсказания. Об истории, онтологии и вычислениях Леннарда-Джонезиума» . Исследования по истории и философии науки . 103 : 105–113. дои : 10.1016/j.shpsa.2023.11.007 . ПМИД 38128443 .

[25] Стефан, Саймон; Тол, Моника; Врабец, Ядран; Хассе, Ганс (28 октября 2019 г.). «Теплофизические свойства жидкости Леннарда-Джонса: база данных и оценка данных» . Журнал химической информации и моделирования . 59 (10): 4248–4265. doi : 10.1021/acs.jcim.9b00620 . ISSN 1549-9596 . ПМИД 31609113 .

[26] «Потенциал Леннарда-Джонса — LibreTexts по химии» . 22 августа 2020 г. Архивировано из оригинала 22 августа 2020 г. Проверено 20 мая 2021 г.

[27] «14.11: Реальные и идеальные газы — LibreTexts по химии» . 06.02.2021. Архивировано из оригинала 06 февраля 2021 г. Проверено 20 мая 2021 г.

[28] Андерсон, стр. 289–291.

[29] Джон, стр.205

[30] Джон, стр. 247–56.

[Oxford_Reference-31] «Постоянный газ» . www.oxfordreference.com . Издательство Оксфордского университета . Проверено 3 апреля 2021 г.

[32] Макферсон, стр. 52–55.

[33] Макферсон, стр. 55–60.

[34] Джон П. Миллингтон (1906). Джон Далтон . стр. 72, 77–78.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

v т и Состояния материи ( список )
State	Solid Liquid Gas / Vapor Supercritical fluid Plasma
Low energy	Bose–Einstein condensate Fermionic condensate Degenerate matter Quantum Hall Rydberg matter Strange matter Superfluid Supersolid Photonic molecule
High energy	QCD matter Quark–gluon plasma Color-glass condensate
Other states	Colloid Crystal Liquid crystal Time crystal Quantum spin liquid Exotic matter Programmable matter Dark matter Antimatter Magnetically ordered Antiferromagnet Ferrimagnet Ferromagnet String-net liquid Superglass
Transitions	Boiling Boiling point Condensation Critical line Critical point Crystallization Deposition Evaporation Flash evaporation Freezing Chemical ionization Ionization Lambda point Melting Melting point Recombination Regelation Saturated fluid Sublimation Supercooling Triple point Vaporization Vitrification
Quantities	Enthalpy of fusion Enthalpy of sublimation Enthalpy of vaporization Latent heat Latent internal energy Trouton's rule Volatility
Concepts	Baryonic matter Binodal Compressed fluid Cooling curve Equation of state Leidenfrost effect Macroscopic quantum phenomena Mpemba effect Order and disorder (physics) Spinodal Superconductivity Superheated vapor Superheating Thermo-dielectric effect

Базы данных авторитетного контроля
National	France BnF data Germany Israel United States Latvia Japan Czech Republic
Other	NARA