Симметричная разница

Симметричная разница
	Венна Диаграмма . Симметричная разность — объединение без пересечения это :
Тип	Установить операцию
Поле	Теория множеств
Заявление	Симметричная разность — это набор элементов, находящихся в любом наборе, но не на пересечении.
Символическое заявление

В математике симметричная разность двух множеств , также известная как дизъюнктивное объединение и сумма множеств , — это набор элементов, которые находятся в любом из множеств, но не в их пересечении. Например, симметричная разность множеств $\{1,2,3\}$ и $\{3,4\}$ является $\{1,2,4\}$ .

Симметричную разность множеств A и B обычно обозначают через $A\operatorname {\Delta } B$ (альтернативно, $A\operatorname {\vartriangle } B$ ), $A\oplus B$ , или $A\ominus B$ .Его можно рассматривать как форму сложения по модулю 2 .

Набор степеней любого набора становится абелевой группой в результате операции симметричной разности, при этом пустой набор является нейтральным элементом группы, а каждый элемент в этой группе является своим собственным обратным . Набор степеней любого набора становится булевым кольцом с симметричной разницей в виде сложения кольца и пересечением в виде умножения кольца.

Характеристики

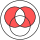
Симметричная разность эквивалентна объединению обоих относительных дополнений , то есть: ^[1]

A\,\Delta \,B=\left(A\setminus B\right)\cup \left(B\setminus A\right),

Симметричную разницу также можно выразить с помощью операции XOR ⊕ над предикатами, описывающими два набора в нотации построителя множеств :

A\mathbin {\Delta } B=\{x:(x\in A)\oplus (x\in B)\}.

Тот же факт можно констатировать и в качестве индикаторной функции (обозначаемой здесь $\chi$ ) симметричной разности, представляющей собой XOR (или сложение по модулю 2 ) индикаторных функций двух ее аргументов: $\chi _{(A\,\Delta \,B)}=\chi _{A}\oplus \chi _{B}$ или используя скобки Айверсона обозначение $[x\in A\,\Delta \,B]=[x\in A]\oplus [x\in B]$ .

Симметричную разность также можно выразить как объединение двух множеств за вычетом их пересечения :

A\,\Delta \,B=(A\cup B)\setminus (A\cap B),

^[1]

В частности, $A\mathbin {\Delta } B\subseteq A\cup B$ ; равенство в этом нестрогом включении имеет место тогда и только тогда, когда $A$ и $B$ являются непересекающимися множествами . Кроме того, обозначая $D=A\mathbin {\Delta } B$ и $I=A\cap B$ , затем $D$ и $I$ всегда непересекающиеся, поэтому $D$ и $I$ раздел $A\cup B$ . Следовательно, если предположить пересечение и симметричную разность как примитивные операции, объединение двух множеств можно корректно определить в терминах симметричной разности с помощью правой части равенства

A\,\cup \,B=(A\,\Delta \,B)\,\Delta \,(A\cap B)

.

Симметричная разность коммутативна и ассоциативна :

{\begin{aligned}A\,\Delta \,B&=B\,\Delta \,A,\\(A\,\Delta \,B)\,\Delta \,C&=A\,\Delta \,(B\,\Delta \,C).\end{aligned}}

Пустое множество нейтрально : , и каждое множество является своим обратным

{\begin{aligned}A\,\Delta \,\varnothing &=A,\\A\,\Delta \,A&=\varnothing .\end{aligned}}

Таким образом, степенное множество любого множества X становится абелевой группой при выполнении операции симметричной разности. (В более общем смысле, любое поле множеств образует группу с симметричной разницей в качестве операции.) Группа, в которой каждый элемент является собственным обратным (или, что то же самое, в которой каждый элемент имеет порядок 2), иногда называется булевой группой ; ^[2]^[3] симметричное различие представляет собой прототипный пример таких групп. Иногда булева группа фактически определяется как операция симметричной разности на множестве. ^[4] В случае, когда X имеет только два элемента, полученная таким образом группа является четырехгруппой Клейна .

Эквивалентно, булева группа — это элементарная абелева 2-группа . Следовательно, группа, индуцированная симметричной разностью, на самом деле является векторным пространством над полем с двумя элементами Z ₂ . Если X конечно, то синглтоны образуют основу этого векторного пространства, и поэтому его размерность равна количеству элементов X . Эта конструкция используется в теории графов для определения пространства циклов графа.

Из свойства инверсий в булевой группе следует, что симметричная разность двух повторяющихся симметричных разностей эквивалентна повторяющейся симметричной разности соединения двух мультимножеств, где для каждого двойного набора оба могут быть удалены. В частности:

(A\,\Delta \,B)\,\Delta \,(B\,\Delta \,C)=A\,\Delta \,C.

Отсюда следует неравенство треугольника: ^[5] симметричная разность А и С содержится в объединении симметричной разности А и В разности В и С. и

Пересечение распределяет по симметричной разности:

A\cap (B\,\Delta \,C)=(A\cap B)\,\Delta \,(A\cap C),

и это показывает, что набор степеней X становится кольцом с симметричной разницей в виде сложения и пересечением в виде умножения. Это прототип булевого кольца .

Дополнительные свойства симметричной разности включают:

$A\mathbin {\Delta } B=\emptyset$ тогда и только тогда, когда $A=B$ .
$A\mathbin {\Delta } B=A^{c}\mathbin {\Delta } B^{c}$ , где $A^{c}$ , $B^{c}$ является $A$ дополнение, $B$ соответственно, относительно любого (фиксированного) набора, содержащего оба.
$\left(\bigcup _{\alpha \in {\mathcal {I}}}A_{\alpha }\right)\Delta \left(\bigcup _{\alpha \in {\mathcal {I}}}B_{\alpha }\right)\subseteq \bigcup _{\alpha \in {\mathcal {I}}}\left(A_{\alpha }\mathbin {\Delta } B_{\alpha }\right)$ , где ${\mathcal {I}}$ — произвольное непустое множество индексов.
Если $f:S\rightarrow T$ любая функция и $A,B\subseteq T$ есть ли какие-либо наборы в $f$ кодомен, тогда $f^{-1}\left(A\mathbin {\Delta } B\right)=f^{-1}\left(A\right)\mathbin {\Delta } f^{-1}\left(B\right).$

Симметричную разность можно определить в любой булевой алгебре , написав

x\,\Delta \,y=(x\lor y)\land \lnot (x\land y)=(x\land \lnot y)\lor (y\land \lnot x)=x\oplus y.

Эта операция имеет те же свойства, что и симметричная разность множеств.

n -арная симметричная разность

Повторяющаяся симметричная разность в некотором смысле эквивалентна операции над множеством наборов (возможно, с несколькими появлениями одного и того же набора), дающей набор элементов, находящихся в нечетном количестве наборов.

Симметричная разность коллекции множеств содержит только элементы, находящиеся в нечетном количестве множеств в коллекции: $\Delta M=\left\{a\in \bigcup M:\left|\{A\in M:a\in A\}\right|{\text{ is odd}}\right\}.$

Очевидно, это корректно определено только тогда, когда каждый элемент объединения ${\textstyle \bigcup M}$ вклад вносится конечным числом элементов $M$ .

Предполагать $M=\left\{M_{1},M_{2},\ldots ,M_{n}\right\}$ является мультимножеством и $n\geq 2$ . Тогда есть формула $|\Delta M|$ , количество элементов в $\Delta M$ , заданный исключительно через пересечения элементов $M$ : $|\Delta M|=\sum _{l=1}^{n}(-2)^{l-1}\sum _{1\leq i_{1}<i_{2}<\ldots <i_{l}\leq n}\left|M_{i_{1}}\cap M_{i_{2}}\cap \ldots \cap M_{i_{l}}\right|.$

Симметричная разность в пространствах с мерой

Пока существует понятие «насколько велико» множество, симметричную разницу между двумя наборами можно считать мерой того, насколько «далеко друг от друга» они находятся.

Сначала рассмотрим конечное множество S и считающую меру подмножеств, определяемую их размером. Теперь рассмотрим два подмножества S и определим расстояние между ними как размер их симметричной разницы. Это расстояние на самом деле является метрикой , что делает набор степеней на S метрическим пространством . Если S имеет n элементов, то расстояние от пустого множества до S равно n , и это максимальное расстояние для любой пары подмножеств. ^[6]

Используя идеи теории меры , разделение измеримых множеств можно определить как меру их симметричной разности. Если µ — σ-конечная мера , определенная на σ-алгебре Σ, функция

d_{\mu }(X,Y)=\mu (X\,\Delta \,Y)

является псевдометрикой на Σ. d _µ становится метрикой , если Σ рассматривается по модулю отношения эквивалентности X ~ Y тогда и только тогда, когда $\mu (X\,\Delta \,Y)=0$ . Иногда ее называют метрикой Фреше - Никодима . Полученное метрическое пространство сепарабельно тогда и только тогда, когда L ²(m) сепарабельна.

Если $\mu (X),\mu (Y)<\infty$ , у нас есть: $|\mu (X)-\mu (Y)|\leq \mu (X\,\Delta \,Y)$ . Действительно,

{\begin{aligned}|\mu (X)-\mu (Y)|&=\left|\left(\mu \left(X\setminus Y\right)+\mu \left(X\cap Y\right)\right)-\left(\mu \left(X\cap Y\right)+\mu \left(Y\setminus X\right)\right)\right|\\&=\left|\mu \left(X\setminus Y\right)-\mu \left(Y\setminus X\right)\right|\\&\leq \left|\mu \left(X\setminus Y\right)\right|+\left|\mu \left(Y\setminus X\right)\right|\\&=\mu \left(X\setminus Y\right)+\mu \left(Y\setminus X\right)\\&=\mu \left(\left(X\setminus Y\right)\cup \left(Y\setminus X\right)\right)\\&=\mu \left(X\,\Delta \,Y\right)\end{aligned}}

Если $S=\left(\Omega ,{\mathcal {A}},\mu \right)$ является пространством меры и $F,G\in {\mathcal {A}}$ являются измеримыми множествами, то их симметричная разность также измерима: $F\Delta G\in {\mathcal {A}}$ . Можно определить отношение эквивалентности на измеримых множествах, полагая $F$ и $G$ быть родственником, если $\mu \left(F\Delta G\right)=0$ . Это отношение обозначается $F=G\left[{\mathcal {A}},\mu \right]$ .

Данный ${\mathcal {D}},{\mathcal {E}}\subseteq {\mathcal {A}}$ , пишет один ${\mathcal {D}}\subseteq {\mathcal {E}}\left[{\mathcal {A}},\mu \right]$ если каждому $D\in {\mathcal {D}}$ есть некоторые $E\in {\mathcal {E}}$ такой, что $D=E\left[{\mathcal {A}},\mu \right]$ . Отношение " $\subseteq \left[{\mathcal {A}},\mu \right]$ " представляет собой частичный порядок в семействе подмножеств ${\mathcal {A}}$ .

Мы пишем ${\mathcal {D}}={\mathcal {E}}\left[{\mathcal {A}},\mu \right]$ если ${\mathcal {D}}\subseteq {\mathcal {E}}\left[{\mathcal {A}},\mu \right]$ и ${\mathcal {E}}\subseteq {\mathcal {D}}\left[{\mathcal {A}},\mu \right]$ . Отношение " $=\left[{\mathcal {A}},\mu \right]$ «является отношением эквивалентности между подмножествами ${\mathcal {A}}$ .

Симметричное закрытие ${\mathcal {D}}$ это совокупность всех ${\mathcal {A}}$ -измеримые множества, которые $=\left[{\mathcal {A}},\mu \right]$ некоторым $D\in {\mathcal {D}}$ . Симметричное закрытие ${\mathcal {D}}$ содержит ${\mathcal {D}}$ . Если ${\mathcal {D}}$ является суб- $\sigma$ -алгебра ${\mathcal {A}}$ , так же как и симметричное замыкание ${\mathcal {D}}$ .

$F=G\left[{\mathcal {A}},\mu \right]$ если только $\left|\mathbf {1} _{F}-\mathbf {1} _{G}\right|=0$ $\left[{\mathcal {A}},\mu \right]$ почти везде .

Расстояние Хаусдорфа против симметричной разности

Расстояние Хаусдорфа и (площадь) симметричной разности являются псевдометриками множества измеримых геометрических фигур. Однако они ведут себя совсем по-другому. На рисунке справа показаны две последовательности фигур: «Красный» и «Красный ∪ Зеленый». Когда расстояние Хаусдорфа между ними становится меньше, площадь симметричной разницы между ними становится больше, и наоборот. Продолжая эти последовательности в обоих направлениях, можно получить две последовательности, в которых расстояние Хаусдорфа между ними сходится к 0, а симметричное расстояние между ними расходится, или наоборот.

См. также

Ссылки

^ Jump up to: ^а ^б Тейлор, Кортни (31 марта 2019 г.). «Что такое симметричная разница в математике?» . МысльКо . Проверено 05 сентября 2020 г.
^ Живант, Стивен; Халмос, Пол (2009). Введение в булеву алгебру . Springer Science & Business Media. п. 6. ISBN 978-0-387-40293-2 .
^ Хамберстон, Ллойд (2011). Соединения . МТИ Пресс. п. 782 . ISBN 978-0-262-01654-4 .
^ Ротман, Джозеф Дж. (2010). Продвинутая современная алгебра . Американское математическое соц. п. 19. ISBN 978-0-8218-4741-1 .
^ Рудин, Вальтер (1 января 1976 г.). Принципы математического анализа (3-е изд.). Макгроу-Хилл Образование. п. 306 . ISBN 978-0070542358 .
^ Клод Фламан (1963) Применение теории графов к групповой структуре , стр. 16, Prentice-Hall MR 0157785

Библиография

Халмос, Пол Р. (1960). Наивная теория множеств . Университетская серия по математике для студентов. Компания Ван Ностранд. Збл 0087.04403 .
Симметричная разность множеств . В энциклопедии математики

[:0-1] Jump up to: ^а ^б Тейлор, Кортни (31 марта 2019 г.). «Что такое симметричная разница в математике?» . МысльКо . Проверено 05 сентября 2020 г.

[GivantHalmos2009-2] Живант, Стивен; Халмос, Пол (2009). Введение в булеву алгебру . Springer Science & Business Media. п. 6. ISBN 978-0-387-40293-2 .

[Humberstone2011-3] Хамберстон, Ллойд (2011). Соединения . МТИ Пресс. п. 782 . ISBN 978-0-262-01654-4 .

[Rotman2010-4] Ротман, Джозеф Дж. (2010). Продвинутая современная алгебра . Американское математическое соц. п. 19. ISBN 978-0-8218-4741-1 .

[5] Рудин, Вальтер (1 января 1976 г.). Принципы математического анализа (3-е изд.). Макгроу-Хилл Образование. п. 306 . ISBN 978-0070542358 .

[6] Клод Фламан (1963) Применение теории графов к групповой структуре , стр. 16, Prentice-Hall MR 0157785

[1]

[2]

[3]

[4]

[5]

[6]

v т и Теория множеств
Overview	Set (mathematics)
Axioms	Adjunction Choice countable dependent global Constructibility (V=L) Determinacy Extensionality Infinity Limitation of size Pairing Power set Regularity Union Martin's axiom Axiom schema replacement specification
Operations	Cartesian product Complement (i.e. set difference) De Morgan's laws Disjoint union Identities Intersection Power set Symmetric difference Union
Concepts Methods	Almost Cardinality Cardinal number (large) Class Constructible universe Continuum hypothesis Diagonal argument Element ordered pair tuple Family Forcing One-to-one correspondence Ordinal number Set-builder notation Transfinite induction Venn diagram
Set types	Amorphous Countable Empty Finite (hereditarily) Filter base subbase Ultrafilter Fuzzy Infinite (Dedekind-infinite) Recursive Singleton Subset · Superset Transitive Uncountable Universal
Theories	Alternative Axiomatic Naive Cantor's theorem Zermelo General Principia Mathematica New Foundations Zermelo–Fraenkel von Neumann–Bernays–Gödel Morse–Kelley Kripke–Platek Tarski–Grothendieck
Paradoxes Problems	Russell's paradox Suslin's problem Burali-Forti paradox
Set theorists	Paul Bernays Georg Cantor Paul Cohen Richard Dedekind Abraham Fraenkel Kurt Gödel Thomas Jech John von Neumann Willard Quine Bertrand Russell Thoralf Skolem Ernst Zermelo