Диэлектрическая проницаемость

Диэлектрическая среда, демонстрирующая ориентацию заряженных частиц, создающую эффекты поляризации. Такая среда может иметь более низкое отношение электрического потока к заряду (большую диэлектрическую проницаемость), чем пустое пространство.

В электромагнетизме абсолютная диэлектрическая проницаемость , часто называемая просто диэлектрической проницаемостью и обозначаемая греческой буквой $ε$ ( эпсилон является мерой электрической поляризуемости диэлектрического ) , материала. Материал с высокой диэлектрической проницаемостью поляризуется сильнее в ответ на приложенное электрическое поле, чем материал с низкой диэлектрической проницаемостью, тем самым сохраняя больше энергии в материале. В электростатике диэлектрическая проницаемость играет важную роль в емкости конденсатора определении .

В простейшем случае поле электрического смещения $D,$ возникающее в результате приложенного электрического поля E, равно

\mathbf {D} =\varepsilon \ \mathbf {E} ~.

В более общем смысле, диэлектрическая проницаемость является термодинамической функцией состояния . ^[1] Это может зависеть от частоты , величины и направления приложенного поля. Единица в системе СИ измерения диэлектрической проницаемости — фарад на метр (Ф/м).

Диэлектрическая проницаемость часто представляется относительной диэлектрической проницаемостью $ε$ _r , которая представляет собой отношение абсолютной диэлектрической проницаемости $ε$ и диэлектрической проницаемости вакуума $ε$ _0.

\kappa =\varepsilon _{\mathrm {r} }={\frac {\varepsilon }{\varepsilon _{0}}}~.

Эту безразмерную величину также часто и неоднозначно называют диэлектрической проницаемостью . Другой общий термин, используемый как для абсолютной, так и для относительной диэлектрической проницаемости, - это диэлектрическая проницаемость , которая устарела в физике и технике. ^[2] так и по химии. ^[3]

По определению, идеальный вакуум имеет относительную диэлектрическую проницаемость ровно 1, тогда как при стандартной температуре и давлении воздух имеет относительную диэлектрическую проницаемость $ε$ _{r air} ≡ $κ$ _air ≈ 1,0006.

Относительная диэлектрическая проницаемость напрямую связана с электрической восприимчивостью ( $χ$ ) соотношением

\chi =\kappa -1

иначе написано как

\varepsilon =\varepsilon _{\mathrm {r} }\ \varepsilon _{0}=(1+\chi )\ \varepsilon _{0}~.

Термин «диэлектрическая проницаемость» был введен в 1880-х годах Оливером Хевисайдом в дополнение к термину » Томсона (1872) « проницаемость . ^[4]^{[ неуместная цитата ]} , ранее записывавшееся как $p$ Обозначение $ε$ , широко использовалось с 1950-х годов.

Единицы

Единицей диэлектрической проницаемости в системе СИ является фарад на метр (Ф/м или Ф·м). ⁻¹). ^[5]

{\frac {\text{F}}{\text{m}}}={\frac {\text{C}}{{\text{V}}{\cdot }{\text{m}}}}={\frac {{\text{C}}^{2}}{{\text{N}}{\cdot }{\text{m}}^{2}}}={\frac {{\text{C}}^{2}{\cdot }{\text{s}}^{2}}{{\text{kg}}{\cdot }{\text{m}}^{3}}}={\frac {{\text{A}}^{2}{\cdot }{\text{s}}^{4}}{{\text{kg}}{\cdot }{\text{m}}^{3}}}

Объяснение

В электромагнетизме поле электрического смещения $D$ возникающее в результате присутствия электрического поля $E.$ представляет собой распределение электрических зарядов в данной среде , Это распределение включает миграцию заряда и переориентацию электрического диполя . Ее отношение к диэлектрической проницаемости в очень простом случае линейных, однородных, изотропных материалов с «мгновенной» реакцией на изменения электрического поля таково:

\mathbf {D} =\varepsilon \ \mathbf {E}

где диэлектрическая проницаемость $ε$ является скаляром . Если среда анизотропна , то диэлектрическая проницаемость является тензором второго ранга .

В общем, диэлектрическая проницаемость не является постоянной величиной, поскольку она может меняться в зависимости от положения в среде, частоты приложенного поля, влажности, температуры и других параметров. В нелинейной среде диэлектрическая проницаемость может зависеть от напряженности электрического поля. Диэлектрическая проницаемость как функция частоты может принимать действительные или комплексные значения.

В единицах СИ диэлектрическая проницаемость измеряется в фарадах на метр (Ф/м или А). ²·с ⁴·кг ⁻¹·м ⁻³). Поле смещения $D$ измеряется в единицах кулонов на квадратный метр (Кл/м ²), а электрическое поле $E$ измеряется в вольтах на метр (В/м). $D$ и $E$ описывают взаимодействие между заряженными объектами. $D$ связано с плотностью заряда, связанной с этим взаимодействием, а $E$ связано с силами и разностью потенциалов .

Диэлектрическая проницаемость вакуума

Диэлектрическая проницаемость вакуума $ε$ _o (также называемая диэлектрической проницаемостью свободного пространства или электрической постоянной ) представляет собой соотношение $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ Д / Э ⁠$ в свободном пространстве . Это также появляется в силовой постоянной Кулона ,

k_{\text{e}}={\frac {1}{\ 4\pi \varepsilon _{0}\ }}

Its value isЕго значение ^[6]^[7]

\varepsilon _{0}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {1}{c^{2}\mu _{0}}}\approx 8.854\,187\,8128(13)\times 10^{-12}{\text{ F/m }}

где

$c$ – скорость света в свободном пространстве,
$µ$ _o – вакуумная проницаемость .

Константы $c$ и $µ$ _o были определены в единицах СИ, чтобы иметь точные числовые значения до переопределения базовых единиц СИ в 2019 году . Следовательно, до этой даты $ε$ _o можно было также выразить точно как дробь: $\ {\tfrac {1}{c^{2}\mu _{0}}}={\tfrac {1}{35\,950\,207\,149.472\,7056\pi }}{\text{ F/m}}\$ даже если результат был иррациональным (поскольку дробь содержала $π$ ). ^[8] Напротив, до 2019 года ампер был измеряемой величиной, но с тех пор ампер теперь точно определен, и именно $μ$ _o является экспериментально измеренной величиной (с соответствующей неопределенностью), и, следовательно, таким же является новое определение $ε$ _o ( $c$ 2019 года). остается точно определенным до и после 2019 года).

Относительная диэлектрическая проницаемость

Линейная диэлектрическая проницаемость однородного материала обычно выражается относительно диэлектрической проницаемости свободного пространства как относительная диэлектрическая проницаемость $ε$ _r (также называемая диэлектрической проницаемостью , хотя этот термин устарел и иногда относится только к статической относительной диэлектрической проницаемости при нулевой частоте). В анизотропном материале относительная диэлектрическая проницаемость может быть тензорной, вызывая двойное лучепреломление . Фактическая диэлектрическая проницаемость затем рассчитывается путем умножения относительной диэлектрической проницаемости на $ε$ _o :

\ \varepsilon =\varepsilon _{\mathrm {r} }\ \varepsilon _{0}=(1+\chi )\ \varepsilon _{0}\ ,

где $χ$ (часто пишется $χ$ _e ) — электрическая восприимчивость материала.

Восприимчивость определяется как константа пропорциональности (которая может быть тензором ), связывающая электрическое поле $E$ с плотностью индуцированной диэлектрической поляризации $P,$ такая, что

\ \mathbf {P} \ =\ \varepsilon _{0}\ \chi \ \mathbf {E} \;,

где $ε$ _o — электрическая проницаемость свободного пространства .

Восприимчивость среды связана с ее относительной диэлектрической проницаемостью $ε$ _r соотношением

\chi =\varepsilon _{\mathrm {r} }-1~.

Итак, в случае вакуума

\chi =0~.

Восприимчивость также связана с поляризуемостью отдельных частиц в среде соотношением Клаузиуса-Моссотти .

Электрическое смещение $D$ связано с плотностью поляризации $P$ соотношением

\mathbf {D} =\varepsilon _{0}\ \mathbf {E} +\mathbf {P} =\varepsilon _{0}\ (1+\chi )\ \mathbf {E} =\varepsilon _{\mathrm {r} }\ \varepsilon _{0}\ \mathbf {E} ~.

Диэлектрическая проницаемость $ε$ и проницаемость $µ$ среды вместе определяют фазовую скорость $v = ⁠ c / n ⁠$ электромагнитного излучения через эту среду:

\varepsilon \mu ={\frac {1}{\ v^{2}}}~.

Практическое применение

Определение емкости

Емкость конденсатора зависит от его конструкции и архитектуры, то есть она не меняется при зарядке и разрядке. Формула емкости конденсатора с параллельными пластинами записывается как

C=\varepsilon \ {\frac {A}{d}}

где $A$ - площадь одной пластины, $d$ расстояние между пластинами, а $\varepsilon$ - диэлектрическая проницаемость среды между двумя пластинами. Для конденсатора с относительной диэлектрической проницаемостью $\kappa$ , можно сказать, что

C=\kappa \ \varepsilon _{0}{\frac {A}{d}}

Закон Гаусса

Диэлектрическая проницаемость связана с электрическим потоком (и, как следствие, с электрическим полем) посредством закона Гаусса . Закон Гаусса гласит, что для замкнутой поверхности , $S$ гауссовой

\Phi _{E}={\frac {Q_{\text{enc}}}{\varepsilon _{0}}}=\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} \ ,

где $\Phi _{E}$ - чистый электрический поток, проходящий через поверхность, $Q_{\text{enc}}$ - заряд, заключенный в гауссовой поверхности, $\mathbf {E}$ – вектор электрического поля в данной точке поверхности, а $\mathrm {d} \mathbf {A}$ — вектор дифференциальной площади на гауссовой поверхности.

Если гауссова поверхность равномерно охватывает изолированное симметричное расположение зарядов, формулу можно упростить до

E\ A\ \cos \theta ={\frac {\;Q_{\text{enc}}}{\ \varepsilon _{0}\ }}\ ,

где $\ \theta \$ представляет собой угол между силовыми линиями электрического поля и нормалью (перпендикуляром) к $S$ .

Если все линии электрического поля пересекают поверхность под углом 90 °, формулу можно упростить до

\ E={\frac {\;Q_{\text{enc}}}{\ \varepsilon _{0}\ A\ }}~.

Поскольку площадь поверхности сферы равна $\ 4\pi r^{2}\ ,$ электрическое поле на расстоянии $r$ вдали от однородного сферического расположения зарядов

\ E={\frac {Q}{\ \varepsilon _{0}A\ }}={\frac {Q}{\ \varepsilon _{0}\ \left(4\ \pi \ r^{2}\right)\ }}={\frac {Q}{\ 4\pi \ \varepsilon _{0}\ r^{2}\ }}~.

Эта формула применима к электрическому полю, создаваемому точечным зарядом вне проводящей сферы или оболочки, вне однородно заряженной изолирующей сферы или между пластинами сферического конденсатора.

Дисперсия и причинность

В общем, материал не может поляризоваться мгновенно в ответ на приложенное поле, поэтому более общая формулировка как функция времени такова:

\mathbf {P} (t)=\varepsilon _{0}\int _{-\infty }^{t}\chi \left(t-t'\right)\mathbf {E} \left(t'\right)\,\operatorname {d} t'~.

То есть поляризация представляет собой свертку электрического поля в предыдущие моменты времени с зависящей от времени восприимчивостью, определяемой $χ (Δt)$ . Верхний предел этого интеграла также можно продлить до бесконечности, если определить $χ (Δ t) = 0$ для $Δ t < 0$ . Мгновенный отклик будет соответствовать дельта-функции Дирака восприимчивости $χ (Δt) = χδ (Δt)$ .

Удобно взять преобразование Фурье по времени и записать эту зависимость как функцию частоты. Благодаря теореме о свертке интеграл становится простым произведением:

\ \mathbf {P} (\omega )=\varepsilon _{0}\ \chi (\omega )\ \mathbf {E} (\omega )~.

Эта частотная зависимость восприимчивости приводит к частотной зависимости диэлектрической проницаемости. Форма восприимчивости по частоте характеризует дисперсионные свойства материала.

Более того, тот факт, что поляризация может зависеть только от электрического поля в предыдущие моменты времени (т.е. эффективно $< 0),$ следствие $причинности χ (∆t) = 0 для ∆t,$ накладывает ограничения Крамерса –Кронига на восприимчивость $χ (0 )$ .

Комплексная диэлектрическая проницаемость

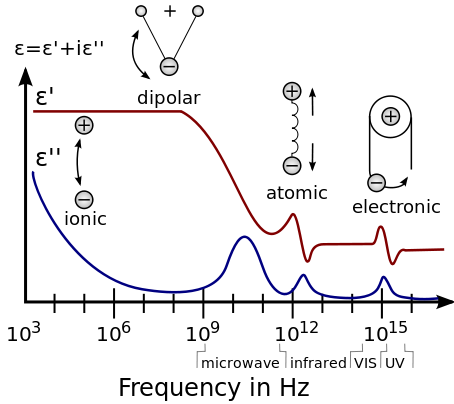
В отличие от реакции вакуума, реакция обычных материалов на внешние поля обычно зависит от частоты поля. Эта частотная зависимость отражает тот факт, что поляризация материала не меняется мгновенно при приложении электрического поля. Реакция всегда должна быть причинной (возникающей после приложенного поля), которую можно представить разностью фаз. По этой причине диэлектрическая проницаемость часто рассматривается как комплексная функция (угловой) частоты $ω$ приложенного поля:

\varepsilon \rightarrow {\hat {\varepsilon }}(\omega )

(поскольку комплексные числа позволяют указать величину и фазу). Таким образом, определение диэлектрической проницаемости становится

D_{0}\ e^{-i\omega t}={\hat {\varepsilon }}(\omega )\ E_{0}\ e^{-i\omega t}\ ,

где

$D$ _o и $E$ _o – амплитуды смещения и электрического поля соответственно,
$я$ - мнимая единица , $я 2 = - 1$ .

Реакция среды на статические электрические поля описывается низкочастотным пределом диэлектрической проницаемости, также называемым статической диэлектрической проницаемостью $ε$ _s (также $ε$ _DC ):

\varepsilon _{\mathrm {s} }=\lim _{\omega \rightarrow 0}{\hat {\varepsilon }}(\omega )~.

На высокочастотном пределе (имеются в виду оптические частоты) комплексную диэлектрическую проницаемость обычно называют $ε$ _∞ (или иногда $ε$ _opt^[10]). На плазменной частоте и ниже диэлектрики ведут себя как идеальные металлы с поведением электронного газа. Статическая диэлектрическая проницаемость является хорошим приближением для переменных полей низких частот, и по мере увеличения частоты $измеримая разность фаз δ$ появляется $между D$ и $E$ . Частота, на которой фазовый сдвиг становится заметным, зависит от температуры и особенностей среды. При умеренной напряженности поля ( $E$ _o ) $D$ и $E$ остаются пропорциональными, и

{\hat {\varepsilon }}={\frac {D_{0}}{E_{0}}}=|\varepsilon |e^{-i\delta }~.

Поскольку реакция материалов на переменные поля характеризуется комплексной диэлектрической проницаемостью, естественно разделить ее действительную и мнимую части, что условно делается следующим образом:

{\hat {\varepsilon }}(\omega )=\varepsilon '(\omega )-i\varepsilon ''(\omega )=\left|{\frac {D_{0}}{E_{0}}}\right|\left(\cos \delta -i\sin \delta \right)~.

где

$ε'$ — действительная часть диэлектрической проницаемости;
$ε″$ — мнимая часть диэлектрической проницаемости;
$δ$ – угол потерь .

Выбор знака зависимости от времени $e - iωt$ , диктует соглашение о знаках для мнимой части диэлектрической проницаемости. Используемые здесь знаки соответствуют знакам, обычно используемым в физике, тогда как по инженерному соглашению следует перевернуть все мнимые величины.

Комплексная диэлектрическая проницаемость обычно является сложной функцией частоты $ω$ , поскольку она представляет собой наложенное описание явлений дисперсии , происходящих на нескольких частотах. Диэлектрическая функция $ε (ω)$ должна иметь полюсы только для частот с положительными мнимыми частями и, следовательно, удовлетворяет соотношениям Крамерса–Кронига . Однако в узких диапазонах частот, которые часто изучаются на практике, диэлектрическая проницаемость может быть аппроксимирована как частотно-независимая, так и модельными функциями.

На данной частоте мнимая часть $ε″$ приводит к потерям на поглощение, если она положительна (в соответствии с приведенным выше соглашением о знаках), и к усилению, если она отрицательна. В более общем смысле следует учитывать мнимые части собственных значений анизотропного диэлектрического тензора.

В случае твердых тел сложная диэлектрическая функция тесно связана с зонной структурой. Основной величиной, характеризующей электронную структуру любого кристаллического материала, является вероятность поглощения фотонов , которая напрямую связана с мнимой частью оптической диэлектрической функции $ε (ω)$ . Оптическая диэлектрическая функция определяется фундаментальным выражением: ^[11]

\varepsilon (\omega )=1+{\frac {8\pi ^{2}e^{2}}{m^{2}}}\sum _{c,v}\int W_{c,v}(E){\bigl (}\varphi (\hbar \omega -E)-\varphi (\hbar \omega +E){\bigr )}\,\operatorname {d} x~.

В этом выражении $W c, v (E)$ представляет собой произведение усредненной по зоне Бриллюэна вероятности перехода при энергии $E$ с совместной плотностью состояний , ^[12]^[13] $J c, v (E)$ ; $φ$ — уширяющая функция, отражающая роль рассеяния в размытии энергетических уровней. ^[14]В общем, уширение является промежуточным между лоренцевым и гауссовым ; ^[15]^[16]для сплава она несколько ближе к гауссовой из-за сильного рассеяния на статистических флуктуациях локального состава в нанометровом масштабе.

Тензорная диэлектрическая проницаемость

Согласно модели Друде намагниченной плазмы, более общее выражение, учитывающее взаимодействие носителей заряда с переменным электрическим полем миллиметрового и микроволнового диапазона в аксиально намагниченном полупроводнике, требует выражения диэлектрической проницаемости в виде недиагонального тензора: ^[17]

\mathbf {D} (\omega )={\begin{vmatrix}\varepsilon _{1}&-i\varepsilon _{2}&0\\i\varepsilon _{2}&\varepsilon _{1}&0\\0&0&\varepsilon _{z}\\\end{vmatrix}}\;\operatorname {\mathbf {E} } (\omega )

Если $ε$ ₂ обращается в нуль, то тензор диагональный, но не пропорционален единице и среда называется одноосной средой, имеющей свойства, подобные одноосному кристаллу .

Классификация материалов

Классификация материалов по диэлектрической проницаемости
$⁠ ε р ″ / ε р' ⁠$	Текущая проводимость	поля Распространение
0		идеальный диэлектрик среда без потерь
≪ 1	материал с низкой проводимостью плохой дирижер	среда с низкими потерями хороший диэлектрик
≈ 1	проводящий материал с потерями	среда распространения с потерями
≫ 1	материал с высокой проводимостью хороший дирижер	среда с высокими потерями плохой диэлектрик
∞	идеальный дирижер

Материалы можно классифицировать в соответствии с их комплексной диэлектрической проницаемостью $ε$ при сравнении ее реальной $ε'$ и мнимой $ε ″$ составляющих (или, что то же самое, σ проводимости $,$ если она учитывается в последнем). Идеальный проводник имеет бесконечную проводимость, $σ = \infty$ , тогда как идеальный диэлектрик — это материал, который вообще не имеет проводимости, $σ = 0$ ; этот последний случай действительной диэлектрической проницаемости (или комплексной диэлектрической проницаемости с нулевой мнимой составляющей) также связан с названием « среда без потерь» . ^[18] Обычно, когда $⁠ σ / ωε' ⁠ ≪ 1$ мы считаем материал диэлектриком с малыми потерями (хотя и не совсем без потерь), тогда как $⁠ σ / ωε' ⁠ ≫ 1$ ассоциируется с хорошим проводником ; такие материалы с немалой проводимостью приводят к большим потерям , которые препятствуют распространению электромагнитных волн, поэтому их также называют средами с потерями . Те материалы, которые не подпадают ни под один из пределов, считаются общими средствами массовой информации.

СМИ с потерями

В случае среды с потерями, т. е. когда током проводимости можно пренебречь, общая плотность протекающего тока равна:

J_{\text{tot}}\ =\ J_{\mathrm {c} }+J_{\mathrm {d} }=\sigma \ E\ +\ i\ \omega \ \varepsilon '\ E=i\ \omega \ {\hat {\varepsilon }}\ E\

где

$σ$ — проводимость среды;
$\ \varepsilon '\ =\ \varepsilon _{0}\ \varepsilon _{\mathsf {r}}\$ – действительная часть диэлектрической проницаемости.
$\ {\hat {\varepsilon }}\ =\ \varepsilon '-i\ \varepsilon ''\$ комплексная диэлектрическая проницаемость

Обратите внимание, что здесь используется электротехническое соглашение о комплексно-сопряженной неоднозначности ; соглашение физики и химии включает в себя комплексно-сопряженное уравнение этих уравнений.

Величина тока смещения зависит от частоты $ω$ приложенного поля $E$ ; в постоянном поле ток смещения отсутствует.

В этом формализме комплексная диэлектрическая проницаемость определяется как: ^[19]^[20]

\ {\hat {\varepsilon }}\ =\ \varepsilon '\left(\ 1\ -\ i\ {\frac {\sigma }{\ \omega \varepsilon '\ }}\ \right)\ =\ \varepsilon '\ -\ i\ {\frac {\ \sigma \ }{\ \omega \ }}

В общем, поглощение электромагнитной энергии диэлектриками обусловлено несколькими различными механизмами, которые влияют на форму диэлектрической проницаемости как функцию частоты:

Во-первых, это эффекты релаксации , связанные с постоянными и индуцированными молекулярными диполями . На низких частотах поле меняется достаточно медленно, чтобы позволить диполям достичь равновесия до того, как поле заметно изменится. Для частот, на которых ориентация диполей не может следовать приложенному полю из-за вязкости среды , поглощение энергии поля приводит к диссипации энергии. Механизм релаксации диполей называется диэлектрической релаксацией и для идеальных диполей описывается классической релаксацией Дебая .
Во-вторых, это резонансные эффекты , которые возникают из-за вращения или вибрации атомов, ионов или электронов . Эти процессы наблюдаются в окрестности характерных для них частот поглощения .

Вышеупомянутые эффекты часто в совокупности вызывают нелинейные эффекты внутри конденсаторов. Например, диэлектрическая абсорбция означает неспособность конденсатора, который заряжался в течение длительного времени, полностью разрядиться при кратковременной разрядке. Хотя идеальный конденсатор после разрядки будет оставаться под напряжением 0 В, реальные конденсаторы будут развивать небольшое напряжение — явление, которое также называется выдержкой или действием батареи . Для некоторых диэлектриков, например многих полимерных пленок, результирующее напряжение может составлять менее 1–2% от исходного напряжения. она может достигать 15–25% Однако в случае электролитических конденсаторов или суперконденсаторов .

Квантово-механическая интерпретация

С точки зрения квантовой механики диэлектрическая проницаемость объясняется атомными и молекулярными взаимодействиями.

На низких частотах молекулы в полярных диэлектриках поляризуются приложенным электрическим полем, которое вызывает периодические вращения. Например, на микроволновой частоте микроволновое поле вызывает периодическое вращение молекул воды, достаточное для разрыва водородных связей . Поле действует против связей, и энергия поглощается материалом в виде тепла . Вот почему микроволновые печи очень хорошо работают с материалами, содержащими воду. Есть два максимума мнимой составляющей (показателя поглощения) воды: один на микроволновой частоте, а другой на частоте дальнего ультрафиолета (УФ). Оба этих резонанса находятся на более высоких частотах, чем рабочая частота микроволновых печей.

На умеренных частотах энергия слишком высока, чтобы вызвать вращение, но слишком мала, чтобы напрямую воздействовать на электроны, и поглощается в форме резонансных молекулярных колебаний. В воде именно здесь показатель поглощения начинает резко падать, а минимум мнимой диэлектрической проницаемости приходится на частоту синего света (оптический режим).

На высоких частотах (таких как УФ и выше) молекулы не могут расслабиться, и энергия полностью поглощается атомами, возбуждая энергетические уровни электронов . Таким образом, эти частоты классифицируются как ионизирующее излучение .

Хотя выполнение полного моделирования ab initio (то есть первых принципов) теперь возможно с помощью вычислений, оно еще не получило широкого применения. Таким образом, феноменологическая модель считается адекватным методом описания экспериментального поведения. Модель Дебая и модель Лоренца используют линейное представление параметров системы с сосредоточенными параметрами первого и второго порядка (соответственно) (например, резонансный контур RC и LRC).

Измерение

Относительную диэлектрическую проницаемость материала можно определить с помощью различных статических электрических измерений. Комплексная диэлектрическая проницаемость оценивается в широком диапазоне частот с использованием различных вариантов диэлектрической спектроскопии , охватывающих почти 21 порядок величины от 10 ⁻⁶ до 10 ¹⁵ герц . Кроме того, с помощью криостатов и печей диэлектрические свойства среды можно охарактеризовать в широком диапазоне температур. Для исследования систем в таких разнообразных полях возбуждения используется ряд измерительных установок, каждая из которых соответствует определенному диапазону частот.

Различные методы микроволновых измерений описаны в Chen et al. . ^[21] Типичные ошибки для метода Хакки – Коулмана, в котором используется шайба материала между проводящими плоскостями, составляют около 0,3%. ^[22]

Низкочастотные измерения во временной области (10 ⁻⁶ до 10 ⁺³ Гц)
низкочастотной частотной Измерения в области (10 ⁻⁵ до 10 ⁺⁶ Гц)
Светоотражающие коаксиальные методы (10 ⁺⁶ до 10 ⁺¹⁰ Гц)
Коаксиальный метод передачи (10 ⁺⁸ до 10 ⁺¹¹ Гц)
Квазиоптические методы (10 ⁺⁹ до 10 ⁺¹⁰ Гц)
Терагерцовая спектроскопия во временной области (10 ⁺¹¹ до 10 ⁺¹³ Гц)
Методы преобразования Фурье (10 ⁺¹¹ до 10 ⁺¹⁵ Гц)

На инфракрасных и оптических частотах распространенным методом является эллипсометрия . Двойная поляризационная интерферометрия также используется для измерения комплексного показателя преломления очень тонких пленок на оптических частотах.

Для трехмерного измерения диэлектрических тензоров на оптической частоте можно использовать диэлектрическую тензорную томографию. ^[23]

См. также

Ссылки

^ Ландау, Л.Д.; Лифшиц, Е.М.; Питаевский, Л.П. (2009). Электродинамика сплошных сред . Эльзевир Баттерворт-Хайнеманн. ISBN 978-0-7506-2634-7 . OCLC 756385298 .
^ Стандартные определения IEEE терминов, касающихся распространения радиоволн (отчет). ИИЭЭ . 1997. с. 6. СТД ИИЭР 211-1997 .
^ Браславский, С.Е. (2007). «Словарь терминов, используемых в фотохимии (рекомендации ИЮПАК, 2006 г.)» (PDF) . Чистая и прикладная химия . 79 (3): 293–465. дои : 10.1351/pac200779030293 . S2CID 96601716 .
^ Флеминг, Джон Амброуз (1910). Принципы электроволновой телеграфии . п. 340.
^ Международное бюро мер и весов (2006 г.), Международная система единиц (СИ) (PDF) (8-е изд.), ISBN 92-822-2213-6 , заархивировано (PDF) из оригинала 04 июня 2021 г. , получено 16 декабря 2021 г. , стр. 119
^ «Значение CODATA 2022: электрическая проницаемость вакуума» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.
^ «Последние (2018 г.) значения констант» . Physics.nist.gov . США Национальный институт стандартов и технологий (NIST). 20 мая 2019 г. Проверено 5 февраля 2022 г.
^ «Последние (2006 г.) значения констант» . Physics.nist.gov . США НИСТ . 01.07.2017 . Проверено 20 ноября 2018 г.
^ «Диэлектрическая спектроскопия» . Архивировано из оригинала 18 января 2006 г. Проверено 20 ноября 2018 г.
^ Хофманн, Филип (26 мая 2015 г.). Физика твердого тела (2-е изд.). Вайли-ВЧ. п. 194. ИСБН 978-352741282-2 . Архивировано из оригинала 18 марта 2020 г. Проверено 28 мая 2019 г.
^ Ю, Питер Ю.; Кардона, Мануэль (2001). Основы полупроводников: Физика и свойства материалов . Берлин: Шпрингер. п. 261. ИСБН 978-3-540-25470-6 .
^ Соле, Хосе Гарсия; Соле, Хосе; Бауса, Луиза (2001). Введение в оптическую спектроскопию неорганических твердых тел . Уайли. Приложение А1, стр. 263. ISBN 978-0-470-86885-0 .
^ Мур, Джон Х.; Спенсер, Николас Д. (2001). Энциклопедия химической физики и физической химии . Тейлор и Фрэнсис. п. 105. ИСБН 978-0-7503-0798-7 .
^ Соле, Хосе Гарсия; Бауса, Луиза Э.; Жак, Даниэль (22 марта 2005 г.). Введение в оптическую спектроскопию неорганических твердых тел . Джон Уайли и сыновья. п. 10. ISBN 978-3-540-25470-6 . Проверено 28 апреля 2024 г.
^ Хауг, Хартмут; Кох, Стефан В. (1994). Квантовая теория оптических и электронных свойств полупроводников . Всемирная научная. п. 196. ИСБН 978-981-02-1864-5 .
^ Разеги, Мание (2006). Основы твердотельной техники . Биркгаузер. п. 383. ИСБН 978-0-387-28152-0 .
^ Прати, Э. (2003). «Распространение в гироэлектромагнитных системах наведения». Журнал электромагнитных волн и приложений . 17 (8): 1177–1196. Бибкод : 2003JEWA...17.1177P . дои : 10.1163/156939303322519810 . S2CID 121509049 .
^ Орфанидис, Софокл Дж. «1: Уравнения Максвелла» (PDF) . Электромагнитные волны и антенны . Университет Рутгерса.
^ Сейболд, Джон С. (2005). Введение в распространение радиочастот . Джон Уайли и сыновья. п. 22, экв. (2.6). ISBN 9780471743682 .
^ Кайзер, Кеннет Л. (2005). Электромагнитное экранирование . ЦРК Пресс. стр. 1–28, ур. (1,80) и (1,81). ISBN 9780849363726 .
^ Чен, Линьфэн; Варадан, В.В.; Онг, СК; Нео, Че По (2004). «СВЧ-теория и методы определения характеристик материалов» . Микроволновая электроника: измерения и характеристика материалов . Уайли. п. 37. ИСБН 978-0-470-84492-2 .
^ Себастьян, Майладил Т. (2008). Диэлектрические материалы для беспроводной связи . Эльзевир. п. 19. ISBN 978-0-08-045330-9 .
^ Шин, Сыну; Ын, Чонхи; Ли, Сан Сок; Ли, Чандже; Югонне, Эрве; Юн, Дон Ки; и др. (2022). «Томографические измерения диэлектрических тензоров на оптической частоте». Природные материалы . 21 : 317–324. дои : 10.1038/s41563-022-01202-8 .

Дальнейшее чтение

Ботчер, CJF; фон Белль, ОК; Бордевейк, Пол (1973). Теория электрической поляризации . Том. 1: Диэлектрическая поляризация. Эльзевир. ISBN 0-444-41579-3 . (том 2 изд. 1978 г.)
фон Хиппель, Артур (1954). Диэлектрики и волны . ISBN 0-89006-803-8 .
фон Хиппель, Артур , изд. (1966). Диэлектрические материалы и их применение: статьи 22 авторов . ISBN 0-89006-805-4 .

Внешние ссылки

«Глава 11» . Lightandmatter.com . Электромагнетизм. Архивировано из оригинала 3 июня 2011 г. — глава из онлайн-учебника

[1] Ландау, Л.Д.; Лифшиц, Е.М.; Питаевский, Л.П. (2009). Электродинамика сплошных сред . Эльзевир Баттерворт-Хайнеманн. ISBN 978-0-7506-2634-7 . OCLC 756385298 .

[IEEE1997-2] Стандартные определения IEEE терминов, касающихся распространения радиоволн (отчет). ИИЭЭ . 1997. с. 6. СТД ИИЭР 211-1997 .

[IUPAC-3] Браславский, С.Е. (2007). «Словарь терминов, используемых в фотохимии (рекомендации ИЮПАК, 2006 г.)» (PDF) . Чистая и прикладная химия . 79 (3): 293–465. дои : 10.1351/pac200779030293 . S2CID 96601716 .

[4] Флеминг, Джон Амброуз (1910). Принципы электроволновой телеграфии . п. 340.

[5] Международное бюро мер и весов (2006 г.), Международная система единиц (СИ) (PDF) (8-е изд.), ISBN 92-822-2213-6 , заархивировано (PDF) из оригинала 04 июня 2021 г. , получено 16 декабря 2021 г. , стр. 119

[physconst-eps0-6] «Значение CODATA 2022: электрическая проницаемость вакуума» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.

[7] «Последние (2018 г.) значения констант» . Physics.nist.gov . США Национальный институт стандартов и технологий (NIST). 20 мая 2019 г. Проверено 5 февраля 2022 г.

[8] «Последние (2006 г.) значения констант» . Physics.nist.gov . США НИСТ . 01.07.2017 . Проверено 20 ноября 2018 г.

[9] «Диэлектрическая спектроскопия» . Архивировано из оригинала 18 января 2006 г. Проверено 20 ноября 2018 г.

[10] Хофманн, Филип (26 мая 2015 г.). Физика твердого тела (2-е изд.). Вайли-ВЧ. п. 194. ИСБН 978-352741282-2 . Архивировано из оригинала 18 марта 2020 г. Проверено 28 мая 2019 г.

[Cardona-11] Ю, Питер Ю.; Кардона, Мануэль (2001). Основы полупроводников: Физика и свойства материалов . Берлин: Шпрингер. п. 261. ИСБН 978-3-540-25470-6 .

[Bausa-12] Соле, Хосе Гарсия; Соле, Хосе; Бауса, Луиза (2001). Введение в оптическую спектроскопию неорганических твердых тел . Уайли. Приложение А1, стр. 263. ISBN 978-0-470-86885-0 .

[Moore-13] Мур, Джон Х.; Спенсер, Николас Д. (2001). Энциклопедия химической физики и физической химии . Тейлор и Фрэнсис. п. 105. ИСБН 978-0-7503-0798-7 .

[Bausa2-14] Соле, Хосе Гарсия; Бауса, Луиза Э.; Жак, Даниэль (22 марта 2005 г.). Введение в оптическую спектроскопию неорганических твердых тел . Джон Уайли и сыновья. п. 10. ISBN 978-3-540-25470-6 . Проверено 28 апреля 2024 г.

[Haug-15] Хауг, Хартмут; Кох, Стефан В. (1994). Квантовая теория оптических и электронных свойств полупроводников . Всемирная научная. п. 196. ИСБН 978-981-02-1864-5 .

[Razeghi-16] Разеги, Мание (2006). Основы твердотельной техники . Биркгаузер. п. 383. ИСБН 978-0-387-28152-0 .

[17] Прати, Э. (2003). «Распространение в гироэлектромагнитных системах наведения». Журнал электромагнитных волн и приложений . 17 (8): 1177–1196. Бибкод : 2003JEWA...17.1177P . дои : 10.1163/156939303322519810 . S2CID 121509049 .

[18] Орфанидис, Софокл Дж. «1: Уравнения Максвелла» (PDF) . Электромагнитные волны и антенны . Университет Рутгерса.

[19] Сейболд, Джон С. (2005). Введение в распространение радиочастот . Джон Уайли и сыновья. п. 22, экв. (2.6). ISBN 9780471743682 .

[20] Кайзер, Кеннет Л. (2005). Электромагнитное экранирование . ЦРК Пресс. стр. 1–28, ур. (1,80) и (1,81). ISBN 9780849363726 .

[Chen-21] Чен, Линьфэн; Варадан, В.В.; Онг, СК; Нео, Че По (2004). «СВЧ-теория и методы определения характеристик материалов» . Микроволновая электроника: измерения и характеристика материалов . Уайли. п. 37. ИСБН 978-0-470-84492-2 .

[Sebastian-22] Себастьян, Майладил Т. (2008). Диэлектрические материалы для беспроводной связи . Эльзевир. п. 19. ISBN 978-0-08-045330-9 .

[23] Шин, Сыну; Ын, Чонхи; Ли, Сан Сок; Ли, Чандже; Югонне, Эрве; Юн, Дон Ки; и др. (2022). «Томографические измерения диэлектрических тензоров на оптической частоте». Природные материалы . 21 : 317–324. дои : 10.1038/s41563-022-01202-8 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]