B 7 Многогранник

Ортографические проекции в _{B 7.} плоскости Кокстера

7-куб

7-ортоплекс

7-демикуб

В 7-мерной геометрии существует 128 однородных многогранников с _B7 симметрией . Существуют две правильные формы: 7-ортоплекс и 8-куб с 14 и 128 вершинами соответственно. 7-демикуб добавлен с половиной симметрии.

Их можно визуализировать как симметричные орфографические проекции в плоскостях Кокстера группы B ₇ Кокстера и других подгрупп.

Графики

Симметричные орфографические проекции этих 128 многогранников можно построить в плоскостях B ₇ , B ₆ , B ₅ , B ₄ , B ₃ , B ₂ , A ₅ , A ₃ , Кокстера . A _k имеет симметрию [k+1] , а B _k имеет симметрию [2k] .

Каждый из этих 128 многогранников показан в этих 8 плоскостях симметрии, с нарисованными вершинами и ребрами, а вершины окрашены в соответствии с количеством перекрывающихся вершин в каждой проективной позиции.

#	плоскости Кокстера Графики								Диаграмма Кокстера-Динкина Символ Шлефли Имя Джонсона и Бауэрса
	Б 7 [14]	Б 6 [12]	Б 5 [10]	Б 4 [8]	BБ3 [6]	BБ2 [4]	AА5 [6]	AА3 [4]
1				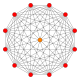					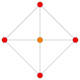{3,3,3,3,3,4} 7-ортоплекс Гекатоникосоктаксон (зее)
2									т 1 {3,3,3,3,3,4} Выпрямленный 7-ортоплекс Гекатоникосоктаксон ректифицированный (рез)
3									т 2 {3,3,3,3,3,4} Биректифицированный 7-ортоплекс Биректифицированный гекатоникоктаксон (барз)
4									т 3 {4,3,3,3,3,3} Триректифицированный 7-куб Гептерактихекатоникосоктаксон (sez)
5									т 2 {4,3,3,3,3,3} Биректифицированный 7-куб Биректифицированный гептеракт (берса)
6									т 1 {4,3,3,3,3,3} Ректифицированный 7-куб Ректифицированный гептеракт (раса)
7									{4,3,3,3,3,3} 7-куб Гептеракт (гепт)
128									ч{4,3,3,3,3,3} 7-демикуб гемигептеракт
8									т 0,1 {3,3,3,3,3,4} Усеченный 7-ортоплекс Усеченный гекатоникосоктаксон (Таз)
9									т 0,2 {3.3.3.3.3.4} Сочлененный 7-ортоплекс Малый ромбированный гекатоникосоктаксон (Сарц)
10									т 1,2 {3,3,3,3,3,4} Битусеченный 7-ортоплекс Двуусеченный гекатоникосоктаксон (Ботаз)
11									т 0,3 {3.3.3.3.3.4} Ранцинированный 7-ортоплекс Мелкопризматический гекатоникоктаксон (Спаз)
12									т 1,3 {3,3,3,3,3,4} Двукантелированный 7-ортоплекс Малый биромбированный гекатоникоктаксон (Себраз)
13									т 2,3 {3,3,3,3,3,4} Трехусеченный 7-ортоплекс Трехусеченный гекатоникосоктаксон (Тотаз)
14									т 0,4 {3.3.3.3.3.4} Стерический 7-ортоплекс Мелкоклеточный гекатоникосоктаксон (Scaz)
15									т 1,4 {3,3,3,3,3,4} Бирунцированный 7-ортоплекс Малый бипризматический гекатоникоктаксон (Сибпаз)
16									т 2,4 {4,3,3,3,3,3} Треугольный 7-куб Малый триромби-гептерактигекатоникосоктаксон (Страсаз)
17									т 2,3 {4,3,3,3,3,3} Трехусеченный 7-куб Трехусеченный гептеракт (Татса)
18									т 0,5 {3,3,3,3,3,4} Пятеричный 7-ортоплекс Малый терированный гекатоникосоктаксон (Стаз)
19									т 1,5 {4,3,3,3,3,3} Бистерифицированный 7-куб. Малый бицелли-гептерактихекатоникосоктаксон (Сабкосаз)
20									т 1,4 {4,3,3,3,3,3} Бирунцированный 7-куб. Малый двупризматический гептеракт (Sibposa)
21									т 1,3 {4,3,3,3,3,3} Двускатный 7-куб Малый бирромбовидный гептеракт (Sibrosa)
22									т 1,2 {4,3,3,3,3,3} Битусеченный 7-куб Усеченный гептеракт (Беца)
23									т 0,6 {4.3.3.3.3.3} Шестигранный 7-куб Малый петигептерактихекатоникосоктаксон (Супозаз)
24									т 0,5 {4,3,3,3,3,3} Пятеричный 7-куб Малый терированный гептеракт (Стеза)
25									т 0,4 {4.3.3.3.3.3} Стерилизованный 7-кубовый Мелкоклеточный гептеракт (Scosa)
26									т 0,3 {4.3.3.3.3.3} Ранцинированный 7-кубовый Малый призматичный гептеракт (Спеса)
27									т 0,2 {4.3.3.3.3.3} Согнутый 7-куб Малый ромбовидный гептеракт (Серса)
28									т 0,1 {4.3.3.3.3.3} Усеченный 7-куб Усеченный гептеракт (Таса)
29									т 0,1,2 {3,3,3,3,3,4} Кантиусеченный 7-ортоплекс Большой ромбированный гекатоникосоктаксон (Гарц)
30									т 0,1,3 {3,3,3,3,3,4} Руноусеченный 7-ортоплекс Призматоусеченный гекатоникоктаксон (Потаз)
31									т 0,2,3 {3,3,3,3,3,4} Рунцикантеллярный 7-ортоплекс Призматоромбатированный гекатоникооктаксон (Парц)
32									т 1,2,3 {3,3,3,3,3,4} Бикантиусеченный 7-ортоплекс Большой биромбатированный гекатоникосоктаксон (Гебраз)
33									т 0,1,4 {3,3,3,3,3,4} Стеритусеченный 7-ортоплекс Целлитусеченный гекатоникосоктаксон (Catz)
34									т 0,2,4 {3,3,3,3,3,4} Стериконтеллярный 7-ортоплекс Целлиромбированный гекатоникосоктаксон (Craze)
35									т 1,2,4 {3,3,3,3,3,4} Бирюроусеченный 7-ортоплекс Бипризматоусеченный гекатоникосоктаксон (Крещение)
36									т 0,3,4 {3,3,3,3,3,4} Стерильный 7-ортоплекс Целлипризматический гекатоникоктаксон (копаз)
37									т 1,3,4 {3,3,3,3,3,4} Бирунчикантеллированный 7-ортоплекс Бипризматоромбатированный гекатоникоктаксон (Бопарз)
38									т 2,3,4 {4,3,3,3,3,3} Трикантиусеченный 7-куб Большой триромби-гептерактихекатонико-октаксон (Готрасаз)
39									т 0,1,5 {3,3,3,3,3,4} Пятиусеченный 7-ортоплекс Теритусеченный гекатоникосоктаксон (Тетаз)
40									т 0,2,5 {3,3,3,3,3,4} Пятиконтеллярный 7-ортоплекс Терирромбированный гекатоникосоктаксон (Тероз)
41									т 1,2,5 {3,3,3,3,3,4} Бистериусеченный 7-ортоплекс Бицеллитусеченный гекатоникоктаксон (Боктаз)
42									т 0,3,5 {3,3,3,3,3,4} Пятиструнный 7-ортоплекс Терипризматический гекатоникоктаксон (Топаз)
43									т 1,3,5 {4,3,3,3,3,3} Бистерикантеллированный, 7-кубовый Бицеллиромби-гептерактихекатоникосоктаксон (Бакресаз)
44									т 1,3,4 {4,3,3,3,3,3} Бирунчикантеллированный 7-куб Бипризматоромбовидный гептеракт (Бопреса)
45									т 0,4,5 {3,3,3,3,3,4} Пентистеризованный 7-ортоплекс Терицеллярный гекатоникосоктаксон (Токаз)
46									т 1,2,5 {4,3,3,3,3,3} Бистериусеченный 7-куб. Гептеракт бицеллитусеченный (Bactasa)
47									т 1,2,4 {4,3,3,3,3,3} Бирюроусеченный 7-куб Гептеракт бипризматоусеченный (Biptesa)
48									т 1,2,3 {4,3,3,3,3,3} Бикантиусеченный 7-куб Большой бирромбовидный гептеракт (Gibrosa)
49									т 0,1,6 {3,3,3,3,3,4} Шестиусеченный 7-ортоплекс Петитусеченный гекатоникосоктаксон (Путаз)
50									т 0,2,6 {3,3,3,3,3,4} Шестикантеллярный 7-ортоплекс Петиромбатированный гекатоникосоктаксон (Пураз)
51									т 0,4,5 {4,3,3,3,3,3} Пентистерифицированный 7-кубовый Терицеллярный гептеракт (Tacosa)
52									т 0,3,6 {4,3,3,3,3,3} Шестиусеченный 7-кубовый Петипризмато-гептерактихекатоникосоктаксон (Пупсез)
53									т 0,3,5 {4,3,3,3,3,3} Пятислойный 7-кубовый Терипризматический гептеракт (Тапса)
54									т 0,3,4 {4,3,3,3,3,3} Стерилизованный 7-кубовый Целлипризматический гептеракт (Капса)
55									т 0,2,6 {4,3,3,3,3,3} Шестикантеллярный 7-куб Петиромбовидный гептеракт (Пуроза)
56									т 0,2,5 {4,3,3,3,3,3} Пятиконтеллярный 7-кубический Терирромбовидный гептеракт (Терса)
57									т 0,2,4 {4,3,3,3,3,3} Стериконтеллярный 7-кубовый Целлиромбовидный гептеракт (Carsa)
58									т 0,2,3 {4,3,3,3,3,3} Рунцикантеллярный 7-куб Призматоромбовидный гептеракт (Парса)
59									т 0,1,6 {4,3,3,3,3,3} Шестиусеченный 7-куб Петитусеченный гептеракт (Пуца)
60									т 0,1,5 {4,3,3,3,3,3} Пятиусеченный 7-куб Теритусеченный гептеракт (Теца)
61									т 0,1,4 {4,3,3,3,3,3} Стерилизованный 7-кубовый Гептеракт целлиусеченный (Catsa)
62									т 0,1,3 {4,3,3,3,3,3} Усеченный 7-куб Гептеракт призматоусеченный (Пеца)
63									т 0,1,2 {4,3,3,3,3,3} Количественный усеченный 7-куб Большой ромбовидный гептеракт (Герса)
64									т 0,1,2,3 {3,3,3,3,3,4} Ранцикантиусеченный 7-ортоплекс Большой призматический гекатоникосоктаксон (Гопаз)
65									т 0,1,2,4 {3,3,3,3,3,4} Стерикантиусеченный 7-ортоплекс Целлигреаторромбовидный гекатоникоктаксон (Когарц)
66									т 0,1,3,4 {3,3,3,3,3,4} Стерирунный усеченный 7-ортоплекс Целлипризматоусеченный гекатоникоктаксон (Каптаз)
67									т 0,2,3,4 {3,3,3,3,3,4} Стерирунцикантеллярный 7-ортоплекс Целлипризматор ромбовидный гекатоникооктаксон (Caparz)
68									т 1,2,3,4 {3,3,3,3,3,4} Бирунцикантиусеченный 7-ортоплекс Большой бипризматический гекатоникоктаксон (Гибпаз)
69									т 0,1,2,5 {3,3,3,3,3,4} Пентикантиусеченный 7-ортоплекс Теригреаторомбатированный гекатоникоктаксон (Тограз)
70									т 0,1,3,5 {3,3,3,3,3,4} Пятиусеченный 7-ортоплекс Терипризматоусеченный гекатоникоктаксон (Топтаз)
71									т 0,2,3,5 {3,3,3,3,3,4} Пятирунцикантеллярный 7-ортоплекс Терипризматоромбатированный гекатоникооктаксон (Топарз)
72									т 1,2,3,5 {3,3,3,3,3,4} Бистерикантиусеченный 7-ортоплекс Бицеллигреатор ромбовидный гекатоникооктаксон (Бекогарц)
73									т 0,1,4,5 {3,3,3,3,3,4} Пентистеритусеченный 7-ортоплекс Терицеллитурированный гекатоникоктаксон (Такотаз)
74									т 0,2,4,5 {3,3,3,3,3,4} Пентистерикантеллированный 7-ортоплекс Терицеллиромбированный гекатоникоктаксон (Tocarz)
75									т 1,2,4,5 {4,3,3,3,3,3} Бистерируглеусеченный 7-куб. Бицеллипризматорунки-гептераактихекатоникосоктаксон (Бокаптозаз)
76									т 0,3,4,5 {3,3,3,3,3,4} Пентистерирцинтированный 7-ортоплекс Терицелпризматический гекатоникоктаксон (Текпаз)
77									т 1,2,3,5 {4,3,3,3,3,3} Бистерический усеченный 7-куб. Бичеллигреатор ромбовидный гептеракт (Бекгреза)
78									т 1,2,3,4 {4,3,3,3,3,3} Бирюнцикантиусеченный 7-кубовый Большой двупризматический гептеракт (Gibposa)
79									т 0,1,2,6 {3,3,3,3,3,4} Гексикантиусеченный 7-ортоплекс Петигреаторомбатированный гекатоникооктаксон (Пугарес)
80									т 0,1,3,6 {3,3,3,3,3,4} Шестиусеченный 7-ортоплекс Петипризматоусеченный гекатоникоктаксон (Папатаз)
81									т 0,2,3,6 {3,3,3,3,3,4} Гексирункантеллированный 7-ортоплекс Петипризматоромбатированный гекатоникооктаксон (Пупарез)
82									т 0,3,4,5 {4,3,3,3,3,3} Пентистеригольчатая 7-кубовая Терицеллипризматический гептеракт (Tecpasa)
83									т 0,1,4,6 {3,3,3,3,3,4} Гексистеритусеченный 7-ортоплекс Петицеллитуретанный гекатоникоктаксон (Пукотаз)
84									т 0,2,4,6 {4,3,3,3,3,3} Гексистерикантеллированный семикубический Петицеллиромби-гептерактихекатоникосоктаксон (Пукросаз)
85									т 0,2,4,5 {4,3,3,3,3,3} Пентистерикантеллированный, 7-кубовый Терицеллиромбовидный гептеракт (Tecresa)
86									т 0,2,3,6 {4,3,3,3,3,3} Шестигранный 7-кубический Петипризматор ромбовидный гептеракт (Пупреса)
87									т 0,2,3,5 {4,3,3,3,3,3} Пятирунчикантеллированный 7-кубический Терипризматор ромбовидный гептеракт (Топреса)
88									т 0,2,3,4 {4,3,3,3,3,3} Стерирунцикантеллярный 7-кубовый Целлипризматор ромбовидный гептеракт (Копреза)
89									т 0,1,5,6 {4,3,3,3,3,3} Гексипентиусеченный 7-куб Петитеритрунки-гептерактихекатоникосоктаксон (Путатозез)
90									т 0,1,4,6 {4,3,3,3,3,3} Гексистериусеченный 7-куб Гептецеллитусеченный гептеракт (Pacutsa)
91									т 0,1,4,5 {4,3,3,3,3,3} Пентистеритусеченный 7-кубический Гептеракт терицеллитусеченный (Tecatsa)
92									т 0,1,3,6 {4,3,3,3,3,3} Шестиусеченный 7-куб Петипризматоусеченный гептеракт (Пупеца)
93									т 0,1,3,5 {4,3,3,3,3,3} Пятикруглоусеченный 7-куб Гептеракт териприсматоусеченный (Toptosa)
94									т 0,1,3,4 {4,3,3,3,3,3} Стерирунный усеченный 7-куб. Гептерак целлипризматоусеченный (Captesa)
95									т 0,1,2,6 {4,3,3,3,3,3} Гексикантиусеченный 7-куб Петигреатор ромбовидный гептеракт (Pugrosa)
96									т 0,1,2,5 {4,3,3,3,3,3} Пентикантиусеченный 7-куб. Теригреаторромбовидный гептеракт (Тогреса)
97									т 0,1,2,4 {4,3,3,3,3,3} Стерикантиусеченный 7-кубовый Целлигреатор ромбовидный гептеракт (Когарса)
98									т 0,1,2,3 {4,3,3,3,3,3} Ранцикантиусеченный 7-куб Большой призматичный гептеракт (Гапса)
99									т 0,1,2,3,4 {3,3,3,3,3,4} Стерирунцикантиусеченный 7-ортоплекс Большой клеточный гекатоникосоктаксон (Гоказ)
100									т 0,1,2,3,5 {3,3,3,3,3,4} Пентирунсикантиусеченный 7-ортоплекс Теригреатопризматический гекатоникоктаксон (Тегопас)
101									т 0,1,2,4,5 {3,3,3,3,3,4} Пентистерикантиусеченный 7-ортоплекс Терицеллигреатор ромбовидный гекатоникооктаксон (Текаграз)
102									т 0,1,3,4,5 {3,3,3,3,3,4} Пентистерирундусеченный 7-ортоплекс Терицеллипризматоусеченный гекатоникооктаксон (Tecpotaz)
103									т 0,2,3,4,5 {3,3,3,3,3,4} Пентистерирункантеллированный 7-ортоплекс Терицеллипризматор ромбовидный гекатоникооктаксон (Такпарес)
104									т 1,2,3,4,5 {4,3,3,3,3,3} Bisteriruncicantitусеченный 7-кубовый Большой бицелли-гептерактихекатоникосоктаксон (Габкозаз)
105									т 0,1,2,3,6 {3,3,3,3,3,4} Шестигранно-усеченный 7-ортоплекс Петигреатопризматический гекатоникоктаксон (Пугопас)
106									т 0,1,2,4,6 {3,3,3,3,3,4} Гексистерикантитусеченный 7-ортоплекс Петицеллигреатор ромбовидный гекатоникооктаксон (Пукаграс)
107									т 0,1,3,4,6 {3,3,3,3,3,4} Гексистерирунно-усеченный 7-ортоплекс Петицеллипризматоусеченный гекатоникоктаксон (Пукпотаз)
108									т 0,2,3,4,6 {4,3,3,3,3,3} Гексистерирунцикантеллярный 7-кубовый Петицеллипризматоромби-гептерактихекатоникосоктаксон (Пукпросаз)
109									т 0,2,3,4,5 {4,3,3,3,3,3} Пентистерирунцикантеллярный, 7-кубический Терицеллипризматор ромбовидный гептеракт (Tocpresa)
110									т 0,1,2,5,6 {3,3,3,3,3,4} Гексипентикантиусеченный 7-ортоплекс Петитереаторомбатированный гекатоникооктаксон (Путеграз)
111									т 0,1,3,5,6 {4,3,3,3,3,3} Шестикругло-усеченный 7-куб. Петитериприсматотрунки-гептерактихекатоникосоктаксон (Путпецаз)
112									т 0,1,3,4,6 {4,3,3,3,3,3} Гексистерирундусеченный 7-куб. Гептеракт петицеллипризматоусеченный (Pucpetsa)
113									т 0,1,3,4,5 {4,3,3,3,3,3} Пентистерирундусеченный 7-кубический Гептеракт терицеллипризматоусеченный (Tecpetsa)
114									т 0,1,2,5,6 {4,3,3,3,3,3} Гексипентикантиусеченный 7-куб. Петитегреаторромбовидный гептеракт (Путгреса)
115									т 0,1,2,4,6 {4,3,3,3,3,3} Гексистерический усеченный 7-куб Петичеллигреатор ромбовидный гептеракт (Pucagrosa)
116									т 0,1,2,4,5 {4,3,3,3,3,3} Пентистерикантиусеченный 7-куб. Терицеллигреатор ромбовидный гептеракт (Tecgresa)
117									т 0,1,2,3,6 {4,3,3,3,3,3} Шестигранно-усеченный 7-куб. Петигреатопризматический гептеракт (Pugopsa)
118									т 0,1,2,3,5 {4,3,3,3,3,3} Пятигранникантиусеченный 7-кубический Теригреатопризматический гептеракт (Тогапса)
119									т 0,1,2,3,4 {4,3,3,3,3,3} Стерирунцикантиусеченный 7-куб. Большой клеточный гептеракт (Gacosa)
120									т 0,1,2,3,4,5 {3,3,3,3,3,4} Пентистерирунцикантиусеченный 7-ортоплекс Большой терированный гекатоникосоктаксон (Готаз)
121									т 0,1,2,3,4,6 {3,3,3,3,3,4} Гексистерирунцикантиусеченный 7-ортоплекс Петигреатоклеточный гекатоникоктаксон (Pugacaz)
122									т 0,1,2,3,5,6 {3,3,3,3,3,4} Гексипентирунсикантиусеченный 7-ортоплекс Петеригреатопризматический гекатоникоктаксон (Путгапаз)
123									т 0,1,2,4,5,6 {4,3,3,3,3,3} Гексипентистерицистантитусеченный 7-куб. Петерицеллигреаторомби-гептерактихекатонико-октаксон (Путчаграсаз)
124									т 0,1,2,3,5,6 {4,3,3,3,3,3} Шестиперикруглый усеченный 7-куб. Петеригреатопризматический гептеракт (Путгапса)
125									т 0,1,2,3,4,6 {4,3,3,3,3,3} Hexisteriruncicantitусеченный 7-кубовый Петигреатоклеточный гептеракт (Pugacasa)
126									т 0,1,2,3,4,5 {4,3,3,3,3,3} Пентистерирунцикантиусеченный 7-куб. Большой терированный гептеракт (Готеса)
127									т 0,1,2,3,4,5,6 {4,3,3,3,3,3} Всеусеченный 7-куб Большой пети-гептерактихекатоникосоктаксон (Гупосаз)

Ссылки

• ХСМ Коксетер :
  • HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
• Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6
  • (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
  • (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
  • (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
• Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
• Клитцинг, Ричард. «7D однородные многогранники (полиекса)» .

Примечания