Фундаментальная пара периодов

В математике фундаментальная пара периодов — это упорядоченная пара комплексных чисел , определяющая решетку на комплексной плоскости . Этот тип решетки является основным объектом, с помощью которого эллиптические функции и модулярные формы определяются .

Определение

Фундаментальная пара периодов – это пара комплексных чисел. $\omega _{1},\omega _{2}\in \mathbb {C}$ такое, что их соотношение $\omega _{2}/\omega _{1}$ не реально. Если рассматривать как векторы в $\mathbb {R} ^{2}$ , они линейно независимы . Решетка, порожденная $\omega _{1}$ и $\omega _{2}$ является

\Lambda =\left\{m\omega _{1}+n\omega _{2}\mid m,n\in \mathbb {Z} \right\}.

Эту решетку иногда обозначают как $\Lambda (\omega _{1},\omega _{2})$ чтобы было ясно, что это зависит от $\omega _{1}$ и $\omega _{2}.$ Его также иногда обозначают $\Omega {\vphantom {(}}$ или $\Omega (\omega _{1},\omega _{2}),$ или просто по $(\omega _{1},\omega _{2}).$ Два генератора $\omega _{1}$ и $\omega _{2}$ называются базисом решетки . Параллелограмм вершинами с $(0,\omega _{1},\omega _{1}+\omega _{2},\omega _{2})$ называется фундаментальным параллелограммом .

Хотя фундаментальная пара порождает решетку, у решетки нет какой-либо уникальной фундаментальной пары; на самом деле одной и той же решетке соответствует бесконечное число фундаментальных пар.

Алгебраические свойства

Можно увидеть ряд объектов недвижимости, перечисленных ниже.

Эквивалентность

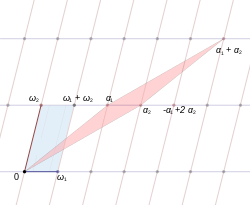
Две пары комплексных чисел $(\omega _{1},\omega _{2})$ и $(\alpha _{1},\alpha _{2})$ называются эквивалентными , если они порождают одну и ту же решетку, т. е. если $\Lambda (\omega _{1},\omega _{2})=\Lambda (\alpha _{1},\alpha _{2}).$

Нет внутренних точек

Фундаментальный параллелограмм не содержит дополнительных точек решетки внутри или на границе. И наоборот, любая пара точек решетки с этим свойством составляет фундаментальную пару и, более того, порождает одну и ту же решетку.

Модульная симметрия

Две пары $(\omega _{1},\omega _{2})$ и $(\alpha _{1},\alpha _{2})$ эквивалентны тогда и только тогда, когда существует $размера 2 \times 2$ матрица ${\textstyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}}$ с целочисленными записями $a,$ $b,$ $c,$ и $d$ и определитель $ad-bc=\pm 1$ такой, что

{\begin{pmatrix}\alpha _{1}\\\alpha _{2}\end{pmatrix}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}\omega _{1}\\\omega _{2}\end{pmatrix}},

то есть, чтобы

{\begin{aligned}\alpha _{1}=a\omega _{1}+b\omega _{2},\\[5mu]\alpha _{2}=c\omega _{1}+d\omega _{2}.\end{aligned}}

Эта матрица принадлежит к модульной группе $\mathrm {SL} (2,\mathbb {Z} ).$ Эту эквивалентность решеток можно рассматривать как основу многих свойств эллиптических функций (особенно эллиптической функции Вейерштрасса ) и модулярных форм.

Топологические свойства

Абелева группа $\mathbb {Z} ^{2}$ отображает комплексную плоскость в фундаментальный параллелограмм. То есть каждая точка $z\in \mathbb {C}$ можно записать как $z=p+m\omega _{1}+n\omega _{2}$ для целых чисел $m,n$ с точкой $p$ в основном параллелограмме.

отображение идентифицирует противоположные стороны параллелограмма как одинаковые, фундаментальный параллелограмм имеет топологию тора Поскольку это . Эквивалентно, говорят, что фактормногообразие $\mathbb {C} /\Lambda$ является тором.

Фундаментальный регион

Серым цветом обозначена каноническая фундаментальная область.

Определять $\tau =\omega _{2}/\omega _{1}$ быть соотношением полупериода . Тогда базис решетки всегда можно выбрать так, что $\tau$ лежит в особой области, называемой фундаментальной областью . С другой стороны, всегда существует элемент проективной специальной линейной группы $\operatorname {PSL} (2,\mathbb {Z} )$ который отображает базис решетки в другой базис так, что $\tau$ лежит в фундаментальной области.

Фундаментальная область задается множеством $D,$ который состоит из набора $U$ плюс часть границы $U$ :

U=\left\{z\in H:\left|z\right|>1,\,\left|\operatorname {Re} (z)\right|<{\tfrac {1}{2}}\right\}.

где $H$ — верхняя полуплоскость .

Фундаментальная область $D$ затем строится путем добавления границы слева плюс половины дуги внизу:

D=U\cup \left\{z\in H:\left|z\right|\geq 1,\,\operatorname {Re} (z)=-{\tfrac {1}{2}}\right\}\cup \left\{z\in H:\left|z\right|=1,\,\operatorname {Re} (z)\leq 0\right\}.

Речь идет о трех случаях:

Если $\tau \neq i$ и ${\textstyle \tau \neq e^{i\pi /3}}$ , то существует ровно два основания решетки с одинаковыми $\tau$ в фундаментальной области: $(\omega _{1},\omega _{2})$ и $(-\omega _{1},-\omega _{2}).$
Если $\tau =i$ , то четыре основания решетки имеют одинаковые $\tau$ : два выше $(\omega _{1},\omega _{2})$ , $(-\omega _{1},-\omega _{2})$ и $(i\omega _{1},i\omega _{2})$ , $(-i\omega _{1},-i\omega _{2}).$
Если ${\textstyle \tau =e^{i\pi /3}}$ , то имеется шесть решетчатых оснований с одинаковыми $\tau$ : $(\omega _{1},\omega _{2})$ , $(\tau \omega _{1},\tau \omega _{2})$ , $(\tau ^{2}\omega _{1},\tau ^{2}\omega _{2})$ и их негативы.

В закрытии фундаментальной области: $\tau =i$ и ${\textstyle \tau =e^{i\pi /3}.}$

См. также

Существует ряд альтернативных обозначений решетки и фундаментальной пары, которые часто используются вместо нее. См., например, статьи о номе , эллиптическом модуле , отношении четверти периода и полупериода .
Эллиптическая кривая
Модульная форма
серия Эйзенштейна

Ссылки

Том М. Апостол , Модульные функции и ряды Дирихле в теории чисел (1990), Springer-Verlag, Нью-Йорк. ISBN 0-387-97127-0 (см. главы 1 и 2).
Юрген Йост, Компактные римановы поверхности (2002), Springer-Verlag, Нью-Йорк. ISBN 3-540-43299-X (см. главу 2.)