Икоситетрагон
| Обычный икоситтрагон | |
|---|---|
 Обычный икоситтрагон | |
| Тип | Правильный многоугольник |
| Ребра и вершины | 24 |
| Символ Шлефли | {24}, т{12}, тт{6}, ттт{3} |
| Диаграммы Кокстера – Дынкина |      |
| Группа симметрии | Двугранник (Д 24 ), заказ 2×24 |
| Внутренний угол ( градусы ) | 165° |
| Характеристики | Выпуклый , циклический , равносторонний , изогональный , изотоксальный |
| Двойной полигон | Себя |
В геометрии икоситетрагон икосикаитетрагон (или ) или 24-угольник — это двадцатичетырёхгранный многоугольник . Сумма внутренних углов любого икоситетрагона равна 3960 градусов.
Обычный икоситтрагон
[ редактировать ]Правильный . икоситетрагон представлен символом Шлефли {24} и также может быть построен в виде усеченного двенадцатиугольника t{12}, дважды усеченного шестиугольника tt{6} или трижды усеченного треугольника ttt{3}
Один внутренний угол правильного икоситетрагона равен 165°, а это означает, что один внешний угол будет равен 15°.
Площадь t правильного икоситетрагона равна: (где = длина ребра)
Икоситетрагон появился в многоугольнике Архимеда, приближенном к числу пи , наряду с шестиугольником (6-угольник), додекагоном (12-угольник), тетраконтаоктагоном (48-угольник) и эннеаконтагексагоном (96-угольник).
Строительство
[ редактировать ]Поскольку 24 = 2 3 × 3, правильный икоситетрагон можно построить с помощью трисектора угла . [1] Как усеченный двенадцатиугольник , он может быть построен путем деления ребра пополам правильного додекагона.
Симметрия
[ редактировать ]
Правильный икоситетрагон имеет Dih 24 симметрию , порядок 48. Существует 7 диэдральных симметрий подгрупп: (Dih 12 , Dih 6 , Dih 3 ) и (Dih 8 , Dih 4 , Dih 2 Dih 1 ) и 8 циклических групповых симметрий: ( Z 24 , Z 12 , Z 6 , Z 3 ) и (Z 8 , Z 4 , Z 2 , Z 1 ).
Эти 16 симметрий можно увидеть в 22 различных симметриях икоситетрагона. Джон Конвей маркирует их буквенным и групповым порядком. [2] Полная симметрия правильной формы равна r48 , а отсутствие симметрии помечено как a1 . Двугранные симметрии делятся в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров), и i , когда линии отражения проходят как через ребра, так и через вершины. Циклические симметрии в среднем столбце обозначены буквой g в соответствии с их центральными порядками вращения.
Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g24 не имеет степеней свободы, но ее можно рассматривать как направленные ребра .
Диссекция
[ редактировать ] обычный |  изотоксал |
Коксетер утверждает, что каждый зоногон (2- метровый угольник, противоположные стороны которого параллельны и одинаковой длины) можно разрезать на m ( m -1)/2 параллелограмма. [3] В частности, это верно для правильных многоугольников с четным числом сторон, и в этом случае все параллелограммы являются ромбами. Для правильного икоситетрагона = 12 , m и его можно разделить на 66: 6 квадратов и 5 наборов по 12 ромбов. Это разложение основано на многоугольника Петри проекции 12-куба .
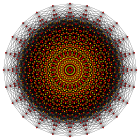 12-кубовый |  |  |  |  |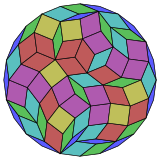
Связанные полигоны
[ редактировать ]
Правильный треугольник, восьмиугольник и икоситетрагон могут полностью заполнять плоскую вершину.
Икоситетраграмма — это 24-гранный звездчатый многоугольник . имеют три правильные формы Символы Шлефли : {24/5}, {24/7} и {24/11}. Есть также 7 обычных звездных фигур, использующих такое же расположение вершин : 2{12}, 3{8}, 4{6}, 6{4}, 8{3}, 3{8/3} и 2{12/. 5}.
| Икоситетраграммы как звездные многоугольники и звездные фигуры |
|---|
Существуют также изогональные икоситетраграммы, построенные как более глубокие усечения правильного додекагона {12} и додекаграммы {12/5}. Они также генерируют два квазиусечения: t{12/11}={24/11} и t{12/7}={24/7}. [4]
| Изогональные усечения правильного додекагона и додекаграммы |
|---|
Косой икоситтрагон
[ редактировать ]| {12}#{ } | {12/5}#{ } | {12/7}#{ } |
|---|---|---|
 |  |  |
| Правильный косой икоситетрагон выглядит как зигзагообразные края додекаграммной антипризмы, додекаграммной антипризмы и додекаграммной скрещенной антипризмы. | ||
Косой икоситетрагон — это косой многоугольник с 24 вершинами и ребрами, но не расположенный в одной плоскости. Внутренняя часть такого икоситетрагона обычно не определена. Косой зигзагообразный икоситтрагон имеет вершины, чередующиеся в двух параллельных плоскостях.
Правильный косой икоситетрагон вершинно -транзитивен с равными длинами ребер. В трехмерном измерении это будет зигзагообразный скошенный икоситетрагон, который можно увидеть в вершинах и боковых гранях двенадцатиугольной антипризмы с тем же D 12d , [2 + ,24] симметрия, порядок 48. Додекаграммная антипризма s{2,24/5} и додекаграммная скрещенная антипризма s{2,24/7} также имеют правильные косые додекагоны.
Полигоны Петри
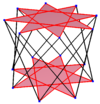
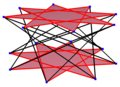
[ редактировать ]Правильный икоситетрагон — это многоугольник Петри для многих многогранников более высокой размерности, рассматриваемых как ортогональные проекции на плоскости Кокстера , в том числе:
| 2F 4 | ||
|---|---|---|
 Усеченный 24-ячеечный |  Ранцинированный 24-клеточный |  Всеусеченный 24-клеточный |
| EЕ8 | ||
|---|---|---|
 4 21 |  2 41 | 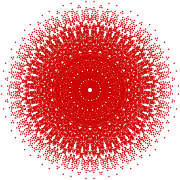 1 42 |
Ссылки
[ редактировать ]- ^ Сборный многоугольник
- ^ Джон Х. Конвей , Хайди Бургель , Хаим Гудман-Штраус , (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шефли, Типы симметрии многоугольника, стр. 275-278)
- ^ Коксетер , Математические развлечения и очерки, тринадцатое издание, стр.141
- ^ Светлая сторона математики: материалы конференции памяти Эжена Стренса по развлекательной математике и ее истории (1994), Метаморфозы многоугольников , Бранко Грюнбаум