Частота вращения
| Частота вращения | |
|---|---|
 | |
Другие имена | скорость вращения, скорость вращения |
Общие символы | , н |
| И объединились | Гц |
Другие подразделения | об/мин , спс |
| В базовых единицах СИ | с -1 |
Выводы из другие количества | ν =ω/(2π рад), n =d N /d t |
| Измерение | |
| Часть серии о |
| Классическая механика |
|---|
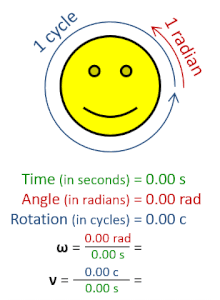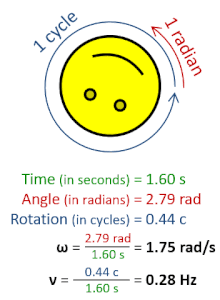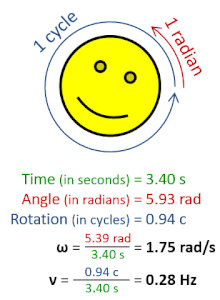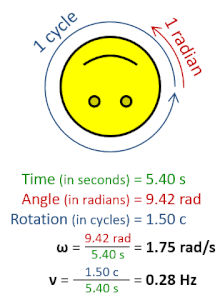
Частота вращения , также известная как скорость вращения или скорость вращения символы ν , строчная греческая буква nu , а также n ), — это частота вращения ( объекта вокруг оси .Его единица СИ — обратные секунды (с). −1 ); другие распространенные единицы измерения включают герцы (Гц), циклы в секунду (cps) и обороты в минуту (об/мин). [1] [а] [б]
Частоту вращения можно получить, разделив угловую частоту ω на полный оборот (2 π радиан ): ν = ω/(2π рад).Его также можно сформулировать как мгновенную скорость изменения числа оборотов N ( по отношению ко времени t : n =d N /d t в соответствии с Международной системой величин ). [4] Подобно обычному периоду , обратной частотой вращения является период вращения или период вращения , T = ν. −1 = п −1 , с измерением времени (единицы СИ — секунды ).
Скорость вращения — векторная величина , величина которой равна скалярной скорости вращения. В особых случаях вращения (вокруг внутренней оси тела) и вращения (внешней оси) скорость вращения можно назвать скоростью вращения и скоростью вращения соответственно.
Ускорение вращения — это скорость изменения скорости вращения; он имеет размерность квадрата обратного времени и единицы СИ квадрата обратных секунд (с −2 ); таким образом, это нормализованная версия углового ускорения , аналогичная бодрости .
Сопутствующие количества
[ редактировать ]Тангенциальная скорость (латинская буква v ), частота вращения и радиальное расстояние , связаны следующим уравнением: [5]
Алгебраическая перестановка этого уравнения позволяет нам определить частоту вращения:
Таким образом, тангенциальная скорость будет прямо пропорциональна когда все части системы одновременно имеют одно и то же , как для колеса, диска или жесткой палочки. Прямая пропорциональность к не справедливо для планет , поскольку планеты имеют разные частоты вращения.
Регрессионный анализ
[ редактировать ]Частота вращения может измерять, например, скорость вращения двигателя. Скорость вращения иногда используется для обозначения угловой частоты, а не величины, определенной в этой статье. Угловая частота дает изменение угла выражается в единице радиан в секунду в единицу времени, которое в системе СИ . Поскольку 2π радиан или 360 градусов соответствуют циклу, мы можем преобразовать угловую частоту в частоту вращения с помощью где
- частота вращения, с единичными циклами в секунду
- - угловая частота, единица радиан в секунду или градус в секунду.
Например, шаговый двигатель может совершать ровно один полный оборот в секунду.Его угловая частота составляет 360 градусов в секунду (360°/с), или 2π радиан в секунду (2π рад/с), а частота вращения — 60 об/мин.
Частоту вращения не следует путать с тангенциальной скоростью , несмотря на некоторую связь между этими двумя понятиями. Представьте себе карусель с постоянной скоростью вращения. Независимо от того, насколько близко или далеко от оси вращения вы находитесь, ваша частота вращения останется постоянной. Однако ваша тангенциальная скорость не остается постоянной. Если вы стоите в двух метрах от оси вращения, ваша тангенциальная скорость будет вдвое больше, чем если бы вы стояли всего в одном метре от оси вращения.
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ «Частота вращения n вращающегося тела определяется как количество оборотов, которые оно совершает за интервал времени, деленный на этот интервал времени [4: ISO 80000-3]. Таким образом, единицей этой величины в системе СИ является обратная секунда ( с −1 ). Однако, как указано в исх. [4: ISO 80000-3], обозначения «обороты в секунду» (об/с) и «обороты в минуту» (об/мин) широко используются в качестве единиц измерения частоты вращения в спецификациях на вращающиеся машины». [2]
- ^ «Единица частоты СИ — герц, единица угловой скорости и угловой частоты СИ — радиан в секунду, а единица активности СИ — беккерель, что подразумевает количество отсчетов в секунду. Хотя формально правильно писать все три эти единицы поскольку обратная секунда, использование разных названий подчеркивает различную природу рассматриваемых величин. Особенно важно тщательно отличать частоты от угловых частот, поскольку по определению их числовые значения отличаются на коэффициент (подробнее см. ISO 80000-3). ] из 2π. Игнорирование этого факта может привести к ошибке 2π. Обратите внимание, что в некоторых странах значения частоты традиционно выражаются с использованием «цикл/с» или «имп/с» вместо единицы измерения СИ, хотя «цикл» и «имп/с». не являются единицами измерения в системе СИ. Также принято, хотя и не рекомендуется, использовать термин «частота» для величин, выраженных в рад/с. По этой причине рекомендуется использовать величины, называемые «частотой», «угловой частотой». и «угловая скорость» всегда выражаются в явных единицах Гц или рад/с, а не с. −1 ." [3]
Ссылки
[ редактировать ]- ^ Аткинс, Тони; Эскюдье, Марсель (2013). Словарь машиностроения . Издательство Оксфордского университета. ISBN 9780199587438 .
- ^ Томпсон, Эмблер; Тейлор, Барри Н. (04 марта 2020 г.) [02 июля 2009 г.]. «Руководство NIST по использованию международной системы единиц, специальная публикация 811» (изд. 2008 г.). Национальный институт стандартов и технологий . Проверено 17 июля 2023 г. [1]
- ^ Международная система единиц (PDF) (9-е изд.), Международное бюро мер и весов, декабрь 2022 г., ISBN 978-92-822-2272-0
- ^ «ISO 80000-3:2019 Величины и единицы. Часть 3. Пространство и время» (2-е изд.). Международная организация по стандартизации . 2019 . Проверено 23 октября 2019 г. [2] (11 страниц)
- ^ «Вращательные величины» .










