Большой икосаэдр

Большой икосаэдр
Тип	Многогранник Кеплера – Пуансо
звездообразования Ядро	икосаэдр
Элементы	Ф = 20, Е = 30 В = 12 (х = 2)
Лица по бокам	20{3}
Символ Шлефли	{3, 5 ⁄ 2 }
Конфигурация лица	V(5 3 )/2
Символ Витхоффа	5 ⁄ 2 | 2 3
Диаграмма Кокстера
Группа симметрии	I h , H 3 , [5,3], (*532)
Ссылки	Ю 53 , С 69 , Ж 41
Характеристики	Правильный невыпуклый дельтаэдр
(3 5 )/2 ( фигура вершины )	Большой звездчатый додекаэдр ( двойной многогранник )

3D-модель большого икосаэдра.

В геометрии большой икосаэдр — один из четырёх многогранников Кеплера-Пуансо ( невыпуклые правильные многогранники ) с символом Шлефли {3, 5 ⁄ 2 } и Кокстера-Динкина диаграмма . Он состоит из 20 пересекающихся треугольных граней, по пять треугольников, встречающихся в каждой вершине в пентаграммной последовательности.

Большой икосаэдр можно построить аналогично пентаграмме, ее двумерному аналогу, путем расширения ( n –1) -мерных симплексных граней основного n -многогранника (равносторонние треугольники для большого икосаэдра и отрезки прямых для пентаграмма) до тех пор, пока фигура не обретет правильные лица. Гранд -600-ячейку можно рассматривать как ее четырехмерный аналог, использующий тот же процесс.

Строительство

Длина ребра большого икосаэдра равна ${\frac {7+3{\sqrt {5}}}{2}}$ раз больше, чем у исходного икосаэдра.

Изображения

Прозрачная модель	Плотность	Звездчатая диаграмма	Сеть
Прозрачная модель великого икосаэдра (См. также Анимация )	Он имеет плотность 7, как показано на этом поперечном сечении.	Это звездчатая форма икосаэдра, которую Веннингер считает моделью [W41], а также 16-ю из 17 звездочек икосаэдра и 7-ю из 59 звездочек Коксетера .	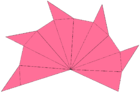× 12 Net (геометрия поверхности); двенадцать равнобедренных пентаграммных пирамид, расположенных как грани додекаэдра. Каждая пирамида складывается веером: пунктирные линии складываются в направлении, противоположном сплошным.

Сферическая черепица

Этот многогранник представляет собой сферическую мозаику с плотностью 7. (Выше показана одна грань сферического треугольника, обведенная синим цветом и закрашенная желтым цветом)

Формулы

Для большого икосаэдра с длиной ребра E:

$${\text{Circumradius}}={{\tfrac {E}{4}}{\Bigl (}{\sqrt {50+22{\sqrt {5}}}}{\Bigr )}}$$

$${\text{Surface Area}}=3{\sqrt {3}}(5+4{\sqrt {5}})E^{2}$$

$${\text{Volume}}={\tfrac {25+9{\sqrt {5}}}{4}}E^{3}$$

В качестве пренебрежения

Большой икосаэдр может быть построен как однородный курносый , с гранями разного цвета и только с тетраэдрической симметрией : . Эту конструкцию можно назвать ретровзносым тетраэдром или ретровзносым тетратетраэдром . аналогично курносой тетраэдрической симметрии икосаэдра ) , как частичная огранка усечённого октаэдра (или омниусечённого тетраэдра : . Его также можно построить с использованием треугольников двух цветов и пиритоэдрической симметрии , как: или , и называется ретровзносым октаэдром .

Тетраэдрический	Пиритоэдрический

Связанные многогранники

Анимированная последовательность усечения от {5/2, 3} до {3, 5/2}

Он имеет то же расположение вершин , что и обычный выпуклый икосаэдр . Он также имеет то же расположение ребер , что и маленький звездчатый додекаэдр .

Операция усечения, неоднократно применяемая к большому икосаэдру, создает последовательность однородных многогранников. Усечение ребер до точек дает большой икосододекаэдр как выпрямленный большой икосаэдр. Процесс завершается биректификацией, уменьшая исходные грани до точек и создавая большой звездчатый додекаэдр .

Усеченный представляет собой вырожденный многогранник с 20 треугольными гранями из усеченных вершин и 12 большой звездчатый додекаэдр (скрытыми) удвоенными пятиугольными гранями ({10/2}) как усеченными исходными гранями пентаграммы, причем последние образуют два больших вписанных додекаэдра. внутри и разделяют края икосаэдра.

Имя	Большой звездчатый додекаэдр	Усеченный большой звездчатый додекаэдр	Большой икосододекаэдр	Усечено большой икосаэдр	Большой икосаэдр
Коксетер-Дынкин диаграмма
Картина

Ссылки

• Веннингер, Магнус (1974). Модели многогранников . Издательство Кембриджского университета . ISBN  0-521-09859-9 .
• Коксетер, Гарольд Скотт Макдональд ; Дю Валь, П.; Флатер, ХТ; Петри, Дж. Ф. (1999). Пятьдесят девять икосаэдров (3-е изд.). Тарквиний. ISBN  978-1-899618-32-3 . МР   0676126 . (1-й Эднский университет Торонто (1938))
• HSM Coxeter , Правильные многогранники , (3-е издание, 1973 г.), Дуврское издание, ISBN   0-486-61480-8 , 3.6 6.2 Стулирование платоновых тел , стр. 96–104

Внешние ссылки

• Вайсштейн, Эрик В. , « Большой икосаэдр » (« Однородный многогранник ») в MathWorld .
  • Вайсштейн, Эрик В. «Пятнадцать звездочек икосаэдра» . Математический мир .
• Однородные многогранники и двойники

Известные звездочки икосаэдра
Обычный	Униформа двойная			Регулярные соединения			Обычная звезда	Другие
(Выпуклый) икосаэдр	Малый триамбический икосаэдр	Медиальный триамбический икосаэдр	Большой триамбический икосаэдр	Соединение пяти октаэдров	Соединение пяти тетраэдров	Соединение десяти тетраэдров	Большой икосаэдр	Раскопанный додекаэдр	Последняя звездочка
Звездчатый процесс на икосаэдре создает ряд родственных многогранников и соединений с икосаэдрической симметрией .