Функция Бесселя

Функции Бесселя описывают радиальную часть колебаний кольцевой мембраны .

Функции Бесселя , впервые определенные математиком Даниэлем Бернулли , а затем обобщенные Фридрихом Бесселем , являются каноническими решениями y ( x ) Бесселя. дифференциального уравнения $$x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}+\left(x^{2}-\alpha ^{2}\right)y=0$$для произвольного комплексного числа $\alpha$, который представляет порядок функции Бесселя. Хотя $\alpha$ и $-\alpha$ создают одно и то же дифференциальное уравнение, для этих двух значений принято определять разные функции Бесселя таким образом, что функции Бесселя в основном являются гладкими функциями $\alpha$.

Наиболее важными являются случаи, когда $\alpha$ является целым или полуцелым числом . Функции Бесселя для целых чисел $\alpha$ также известны как цилиндрические функции или цилиндрические гармоники , поскольку они появляются в решении уравнения Лапласа в цилиндрических координатах . Сферические функции Бесселя с полуцелыми числами $\alpha$ получаются при решении уравнения Гельмгольца в сферических координатах .

Приложения функций Бесселя

Уравнение Бесселя возникает при нахождении разделимых решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических или сферических координатах . Поэтому функции Бесселя особенно важны для многих задач распространения волн и статических потенциалов. При решении задач в цилиндрических системах координат получаются функции Бесселя целого порядка ( α = n ); в сферических задачах получают полуцелые порядки ( α = n + ⁠ 1/2 ​ ⁠ ) . Например:

• Электромагнитные волны в цилиндрическом волноводе
• Амплитуды давления невязких вращательных течений
• Теплопроводность в цилиндрическом объекте
• Режимы вибрации тонкой круглой или кольцевой акустической мембраны (например, пластика барабана или другого мембранофона ) или более толстых пластин, таких как листовой металл (см. Теорию пластин Кирхгофа – Лява , Теорию пластин Миндлина – Рейсснера )
• Проблемы диффузии на решетке
• Решения радиального уравнения Шрёдингера (в сферических и цилиндрических координатах) для свободной частицы
• Представление фейнмановского пропагатора в квантовой теории поля в позиционном пространстве
• Определение закономерностей акустического излучения
• Частотно-зависимое трение в кольцевых трубопроводах
• Динамика плавающих тел
• Угловое разрешение
• Дифракция от спиральных объектов, включая ДНК
• Функция плотности вероятности произведения двух нормально распределенных случайных величин
• Анализ поверхностных волн, генерируемых микротреморами, в геофизике и сейсмологии .

Функции Бесселя появляются и в других задачах, таких как обработка сигналов (например, см. синтез FM-звука , окно Кайзера или фильтр Бесселя ).

Определения

Поскольку это линейное дифференциальное уравнение, решения можно масштабировать до любой амплитуды. Амплитуды, выбранные для функций, взяты из ранних работ, в которых функции появлялись как решения определенных интегралов, а не как решения дифференциальных уравнений. Поскольку дифференциальное уравнение имеет второй порядок, должно быть два линейно независимых решения. Однако в зависимости от обстоятельств удобны различные рецептуры этих растворов. Различные варианты обобщены в таблице ниже и описаны в следующих разделах.

Тип	Первый вид	Второй вид
Функции Бесселя	Дж а	Да ​
Модифицированные функции Бесселя	я α	К α
Функции Ханкеля	ЧАС (1) α = J α + iY α	ЧАС (2) α = J α − iY α
Сферические функции Бесселя	дж н	затем ​
Сферические функции Ханкеля	час (1) п = j n + iy n	час (2) п = j n - iy n

рода иногда обозначаются N _n и nn _n соответственно, а не Y _n и y _{Функции Бесселя второго рода и сферические функции Бесселя второго} .

Функции Бесселя первого рода: J _α

График функции Бесселя первого рода J _n ( z ) с n = 0,5 в комплексной плоскости от −2 − 2 i до 2 + 2 i

График функции Бесселя первого рода J _α ( x ) для целых порядков α = 0, 1, 2

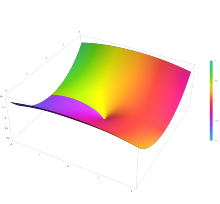
Функции Бесселя первого рода, обозначаемые как J _α ( x ) , являются решениями дифференциального уравнения Бесселя. Для целого или положительного α функции Бесселя первого рода конечны в начале координат ( x = 0 ); в то время как для отрицательных нецелых α функции Бесселя первого рода расходятся при приближении x к нулю. Определить функцию можно с помощью $x^{\alpha }$ раз ряд Маклорена (обратите внимание, что α не обязательно должно быть целым числом, а нецелые степени не допускаются в ряду Тейлора), который можно найти, применив метод Фробениуса к уравнению Бесселя: $$J_{\alpha }(x)=\sum _{m=0}^{\infty }{\frac {(-1)^{m}}{m!\,\Gamma (m+\alpha +1)}}{\left({\frac {x}{2}}\right)}^{2m+\alpha },$$где Γ( z ) — гамма-функция , сдвинутое обобщение факториала на нецелые значения. Функция Бесселя первого рода является целой функцией, если α — целое число, в противном случае — многозначной функцией с особенностью в нуле. Графики функций Бесселя выглядят примерно как колеблющиеся функции синуса или косинуса, которые затухают пропорционально $x^{-{1}/{2}}$ (см. также их асимптотические формы ниже), хотя их корни обычно не являются периодическими, за исключением асимптотически больших x . (Ряд указывает на то, что − J ₁ ( x ) является производной от J ₀ ( x ) , так же, как −sin x является производной от cos x ; в более общем смысле, производная от J _n ( x ) может быть выражена через J _{n ± 1} ( x ) тождествам согласно приведенным ниже .)

Для нецелого числа α функции J _α ( x ) и J _{− α} ( x ) линейно независимы и, следовательно, являются двумя решениями дифференциального уравнения. С другой стороны, для целого порядка n справедливо следующее соотношение (гамма-функция имеет простые полюса для каждого из неположительных целых чисел): $$J_{-n}(x)=(-1)^{n}J_{n}(x).$$

Это означает, что два решения больше не являются линейно независимыми. В этом случае второе линейно независимое решение оказывается функцией Бесселя второго рода, как обсуждается ниже.

Интегралы Бесселя

Другое определение функции Бесселя для целочисленных значений n возможно с использованием интегрального представления: $$J_{n}(x)={\frac {1}{\pi }}\int _{0}^{\pi }\cos(n\tau -x\sin \tau )\,d\tau ={\frac {1}{\pi }}\operatorname {Re} \left(\int _{0}^{\pi }e^{i(n\tau -x\sin \tau )}\,d\tau \right),$$которую еще называют формулой Хансена-Бесселя.

Именно такой подход использовал Бессель. и из этого определения он вывел несколько свойств функции. Определение может быть расширено до нецелых порядков с помощью одного из интегралов Шлефли для Re( x ) > 0 : $$J_{\alpha }(x)={\frac {1}{\pi }}\int _{0}^{\pi }\cos(\alpha \tau -x\sin \tau )\,d\tau -{\frac {\sin(\alpha \pi )}{\pi }}\int _{0}^{\infty }e^{-x\sinh t-\alpha t}\,dt.$$

Связь с гипергеометрическим рядом

Функции Бесселя можно выразить через обобщенный гипергеометрический ряд следующим образом: $$J_{\alpha }(x)={\frac {\left({\frac {x}{2}}\right)^{\alpha }}{\Gamma (\alpha +1)}}\;_{0}F_{1}\left(\alpha +1;-{\frac {x^{2}}{4}}\right).$$

Это выражение связано с развитием функций Бесселя через функцию Бесселя–Клиффорда .

Связь с полиномами Лагерра

Через полиномы Лагерра L _k и произвольно выбранный параметр t функцию Бесселя можно выразить как $${\frac {J_{\alpha }(x)}{\left({\frac {x}{2}}\right)^{\alpha }}}={\frac {e^{-t}}{\Gamma (\alpha +1)}}\sum _{k=0}^{\infty }{\frac {L_{k}^{(\alpha )}\left({\frac {x^{2}}{4t}}\right)}{\binom {k+\alpha }{k}}}{\frac {t^{k}}{k!}}.$$

Функции Бесселя второго рода: Y _α

График функции Бесселя второго рода Y _n ( z ) с n = 0,5 в комплексной плоскости от −2 − 2 i до 2 + 2 i

Функции Бесселя второго рода, обозначаемые Y _α ( x ) , иногда обозначаемые вместо этого N _α ( x ) , являются решениями дифференциального уравнения Бесселя, имеющими особенность в начале координат ( x = 0 ) и многозначными . Их иногда называют функциями Вебера , так как они были введены Х. М. Вебером ( 1873 ), а также функциями Неймана после Карла Неймана .

Для нецелого числа Y α α ₍ x ) связано с J _α ( x ) соотношением $$Y_{\alpha }(x)={\frac {J_{\alpha }(x)\cos(\alpha \pi )-J_{-\alpha }(x)}{\sin(\alpha \pi )}}.$$

В случае целочисленного порядка n функция определяется путем достижения предела, когда нецелое значение α стремится к n : $$Y_{n}(x)=\lim _{\alpha \to n}Y_{\alpha }(x).$$

Если n — целое неотрицательное число, мы имеем ряд

$$Y_{n}(z)=-{\frac {\left({\frac {z}{2}}\right)^{-n}}{\pi }}\sum _{k=0}^{n-1}{\frac {(n-k-1)!}{k!}}\left({\frac {z^{2}}{4}}\right)^{k}+{\frac {2}{\pi }}J_{n}(z)\ln {\frac {z}{2}}-{\frac {\left({\frac {z}{2}}\right)^{n}}{\pi }}\sum _{k=0}^{\infty }(\psi (k+1)+\psi (n+k+1)){\frac {\left(-{\frac {z^{2}}{4}}\right)^{k}}{k!(n+k)!}}$$

График функции Бесселя второго рода Y _α ( x ) для целых порядков α = 0, 1, 2

где $\psi (z)$ — дигамма-функция , логарифмическая производная гамма -функции .

Существует также соответствующая интегральная формула (для Re( x ) > 0 ): $$Y_{n}(x)={\frac {1}{\pi }}\int _{0}^{\pi }\sin(x\sin \theta -n\theta )\,d\theta -{\frac {1}{\pi }}\int _{0}^{\infty }\left(e^{nt}+(-1)^{n}e^{-nt}\right)e^{-x\sinh t}\,dt.$$

В случае, когда n = 0 , $$Y_{0}\left(x\right)={\frac {4}{\pi ^{2}}}\int _{0}^{{\frac {1}{2}}\pi }\cos \left(x\cos \theta \right)\left(e+\ln \left(2x\sin ^{2}\theta \right)\right)\,d\theta .$$

Y _α ( x ) необходим как второе линейно независимое решение уравнения Бесселя, когда α является целым числом. Но Y _α ( x ) имеет большее значение. Его можно рассматривать как «естественного» партнера J _α ( x ) . См. также подраздел о функциях Ханкеля ниже.

Более того, когда α — целое число, как и в случае с функциями первого рода, справедливо следующее соотношение: $$Y_{-n}(x)=(-1)^{n}Y_{n}(x).$$

И J _α ( x ) , и Y _α ( x ) являются голоморфными функциями на x комплексной плоскости, разрезанной вдоль отрицательной вещественной оси. Когда α является целым числом, функции Бесселя являются целыми функциями x J . Если x зафиксирован на ненулевом значении, то функции Бесселя являются целыми функциями от α .

Функции Бесселя второго рода, когда α — целое число, являются примером решения второго рода в теореме Фукса .

Функции Ханкеля: H ⁽¹⁾
_а , ч ⁽²⁾
_а

График функции Ганкеля первого рода H ⁽¹⁾
_n ( x ) с n = −0,5 в комплексной плоскости от −2 − 2 i до 2 + 2 i

График функции Ганкеля второго рода H ⁽²⁾
_n ( x ) с n = −0,5 в комплексной плоскости от −2 − 2 i до 2 + 2 i

Другой важной формулировкой двух линейно независимых решений уравнения Бесселя являются функции Ганкеля первого и второго рода , H ⁽¹⁾
_α ( x ) и H ⁽²⁾
_α ( x ) , определяемый как $${\begin{aligned}H_{\alpha }^{(1)}(x)&=J_{\alpha }(x)+iY_{\alpha }(x),\\[5pt]H_{\alpha }^{(2)}(x)&=J_{\alpha }(x)-iY_{\alpha }(x),\end{aligned}}$$

где я — мнимая единица . Эти линейные комбинации известны также как функции Бесселя третьего рода ; это два линейно независимых решения дифференциального уравнения Бесселя. Они названы в честь Германа Ханкеля .

Эти формы линейной комбинации удовлетворяют многочисленным простым на вид свойствам, таким как асимптотические формулы или интегральные представления. Здесь «простой» означает появление множителя вида e ^{я ж (х)} . Серьезно $x>0$ где $J_{\alpha }(x)$, $Y_{\alpha }(x)$ вещественны, функции Бесселя первого и второго рода представляют собой действительную и мнимую части соответственно первой функции Ганкеля и вещественную и отрицательную мнимую части второй функции Ганкеля. Таким образом, приведенные выше формулы являются аналогами формулы Эйлера с заменой H ⁽¹⁾
_а ( Икс ) , Ч ⁽²⁾
_α ( x ) для $e^{\pm ix}$ и $J_{\alpha }(x)$, $Y_{\alpha }(x)$ для $\cos(x)$, $\sin(x)$, как явно показано в асимптотическом разложении .

Функции Ханкеля используются для выражения цилиндрических волновых решений уравнения цилиндрических волн, распространяющихся наружу и внутрь, соответственно (или наоборот, в зависимости от соглашения о знаках для частоты ).

Используя предыдущие соотношения, их можно выразить как $${\begin{aligned}H_{\alpha }^{(1)}(x)&={\frac {J_{-\alpha }(x)-e^{-\alpha \pi i}J_{\alpha }(x)}{i\sin \alpha \pi }},\\[5pt]H_{\alpha }^{(2)}(x)&={\frac {J_{-\alpha }(x)-e^{\alpha \pi i}J_{\alpha }(x)}{-i\sin \alpha \pi }}.\end{aligned}}$$

Если α является целым числом, необходимо вычислить предел. Следующие отношения действительны независимо от того, является ли α целым числом или нет: $${\begin{aligned}H_{-\alpha }^{(1)}(x)&=e^{\alpha \pi i}H_{\alpha }^{(1)}(x),\\[6mu]H_{-\alpha }^{(2)}(x)&=e^{-\alpha \pi i}H_{\alpha }^{(2)}(x).\end{aligned}}$$

В частности, если α = m + ⁠ 1 / 2 ⁠ , где m — неотрицательное целое число, из приведенных выше соотношений прямо следует, что $${\begin{aligned}J_{-(m+{\frac {1}{2}})}(x)&=(-1)^{m+1}Y_{m+{\frac {1}{2}}}(x),\\[5pt]Y_{-(m+{\frac {1}{2}})}(x)&=(-1)^{m}J_{m+{\frac {1}{2}}}(x).\end{aligned}}$$

Они полезны при разработке сферических функций Бесселя (см. ниже).

Функции Ханкеля допускают следующие интегральные представления для Re( x ) > 0 : $${\begin{aligned}H_{\alpha }^{(1)}(x)&={\frac {1}{\pi i}}\int _{-\infty }^{+\infty +\pi i}e^{x\sinh t-\alpha t}\,dt,\\[5pt]H_{\alpha }^{(2)}(x)&=-{\frac {1}{\pi i}}\int _{-\infty }^{+\infty -\pi i}e^{x\sinh t-\alpha t}\,dt,\end{aligned}}$$где пределы интегрирования обозначают интегрирование по контуру , который можно выбрать следующим образом: от −∞ до 0 по отрицательной действительной оси, от 0 до ± π i по мнимой оси и от ± π i до +∞ ± π i вдоль контур, параллельный действительной оси.

Модифицированные функции Бесселя: I _α , K _α

Функции Бесселя действительны даже для комплексных аргументов x , а важным частным случаем является случай чисто мнимого аргумента. В этом случае решения уравнения Бесселя называются модифицированными функциями Бесселя (или иногда гиперболическими функциями Бесселя ) первого и второго рода и определяются как $${\begin{aligned}I_{\alpha }(x)&=i^{-\alpha }J_{\alpha }(ix)=\sum _{m=0}^{\infty }{\frac {1}{m!\,\Gamma (m+\alpha +1)}}\left({\frac {x}{2}}\right)^{2m+\alpha },\\[5pt]K_{\alpha }(x)&={\frac {\pi }{2}}{\frac {I_{-\alpha }(x)-I_{\alpha }(x)}{\sin \alpha \pi }},\end{aligned}}$$когда α не является целым числом; когда α является целым числом, используется предел. Они выбраны так, чтобы иметь действительные значения для действительных и положительных аргументов x . Таким образом, разложение в ряд для I _α ( x ) аналогично разложению для J _α ( x ) , но без чередующегося (−1) ^м фактор.

$K_{\alpha }$ может быть выражено через функции Ганкеля: $$K_{\alpha }(x)={\begin{cases}{\frac {\pi }{2}}i^{\alpha +1}H_{\alpha }^{(1)}(ix)&-\pi <\arg x\leq {\frac {\pi }{2}}\\{\frac {\pi }{2}}(-i)^{\alpha +1}H_{\alpha }^{(2)}(-ix)&-{\frac {\pi }{2}}<\arg x\leq \pi \end{cases}}$$

Используя эти две формулы, получим результат $J_{\alpha }^{2}(z)$+ $Y_{\alpha }^{2}(z)$, широко известный как интеграл Николсона или формула Николсона, можно получить следующим образом: $$J_{\alpha }^{2}(x)+Y_{\alpha }^{2}(x)={\frac {8}{\pi ^{2}}}\int _{0}^{\infty }\cosh(2\alpha t)K_{0}(2x\sinh t)\,dt,$$

при условии, что условие Re( x ) > 0 выполнено. Также можно показать, что $$J_{\alpha }^{2}(x)+Y_{\alpha }^{2}(x)={\frac {8\cos(\alpha \pi )}{\pi ^{2}}}\int _{0}^{\infty }K_{2\alpha }(2x\sinh t)\,dt,$$

только тогда, когда | Ре(α) | < ⁠ 1/2 , ⁠ x и Re(x) ≥ 0 но не тогда, когда = 0 .

Мы можем выразить первую и вторую функции Бесселя через модифицированные функции Бесселя (они справедливы, если − π < arg z ≤ ⁠ π / 2 ⁠ ): $${\begin{aligned}J_{\alpha }(iz)&=e^{\frac {\alpha \pi i}{2}}I_{\alpha }(z),\\[1ex]Y_{\alpha }(iz)&=e^{\frac {(\alpha +1)\pi i}{2}}I_{\alpha }(z)-{\tfrac {2}{\pi }}e^{-{\frac {\alpha \pi i}{2}}}K_{\alpha }(z).\end{aligned}}$$

I _α ( x ) и K _α ( x ) — два линейно независимых решения модифицированного уравнения Бесселя : $$x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}-\left(x^{2}+\alpha ^{2}\right)y=0.$$

В отличие от обычных функций Бесселя, которые колеблются как функции действительного аргумента, I _α и K _α являются экспоненциально растущими и убывающими функциями соответственно. обычная функция Бесселя Jα _и , функция Iα _{Как и} обращается в ноль при x = 0 при α > 0 конечна при x = 0 при α = 0 . Аналогично, K _α расходится в точке x = 0 с особенностью логарифмического типа для K ₀ , и ⁠ 1 / 2 ⁠ Γ(| а |)(2/ x ) ^{| а |} в противном случае.

Модифицированные функции Бесселя первого рода I α ( x ) для α = 0, 1, 2, 3

Модифицированные функции Бесселя второго рода K α ( x ) для α = 0, 1, 2, 3

Две интегральные формулы для модифицированных функций Бесселя: (для Re( x ) > 0 ): $${\begin{aligned}I_{\alpha }(x)&={\frac {1}{\pi }}\int _{0}^{\pi }e^{x\cos \theta }\cos \alpha \theta \,d\theta -{\frac {\sin \alpha \pi }{\pi }}\int _{0}^{\infty }e^{-x\cosh t-\alpha t}\,dt,\\[5pt]K_{\alpha }(x)&=\int _{0}^{\infty }e^{-x\cosh t}\cosh \alpha t\,dt.\end{aligned}}$$

Функции Бесселя можно описать как преобразования Фурье степеней квадратичных функций. Например (для Re(ω) > 0 ): $$2\,K_{0}(\omega )=\int _{-\infty }^{\infty }{\frac {e^{i\omega t}}{\sqrt {t^{2}+1}}}\,dt.$$

Это можно доказать, показав равенство приведенному выше интегральному определению для K ₀ . Это делается путем интегрирования замкнутой кривой в первом квадранте комплексной плоскости.

Модифицированные функции Бесселя K _1/3 и K _2/3 могут быть представлены в виде быстро сходящихся интегралов. $${\begin{aligned}K_{\frac {1}{3}}(\xi )&={\sqrt {3}}\int _{0}^{\infty }\exp \left(-\xi \left(1+{\frac {4x^{2}}{3}}\right){\sqrt {1+{\frac {x^{2}}{3}}}}\right)\,dx,\\[5pt]K_{\frac {2}{3}}(\xi )&={\frac {1}{\sqrt {3}}}\int _{0}^{\infty }{\frac {3+2x^{2}}{\sqrt {1+{\frac {x^{2}}{3}}}}}\exp \left(-\xi \left(1+{\frac {4x^{2}}{3}}\right){\sqrt {1+{\frac {x^{2}}{3}}}}\right)\,dx.\end{aligned}}$$

Модифицированная функция Бесселя $K_{\frac {1}{2}}(\xi )=(2\xi /\pi )^{-1/2}\exp(-\xi )$ полезно представить распределение Лапласа как смесь нормальных распределений в экспоненциальном масштабе.

Модифицированную функцию Бесселя второго рода также называли следующими именами (ныне редкими):

• Функция бассета в честь Альфреда Барнарда Бассета
• Модифицированная функция Бесселя третьего рода.
• Модифицированная функция Ханкеля
• Функция Макдональда после Гектора Манро Макдональда

Сферические функции Бесселя: j _n , y _n

График сферической функции Бесселя первого рода j _n ( z ) с n = 0,5 в комплексной плоскости от −2 − 2 i до 2 + 2 i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D

График сферической функции Бесселя второго рода y _n ( z ) с n = 0,5 в комплексной плоскости от −2 − 2 i до 2 + 2 i с цветами, созданными с помощью функции Mathematica 13.1 ComplexPlot3D

Сферические функции Бесселя первого рода, j _n ( x ) , для n = 0, 1, 2

Сферические функции Бесселя второго рода, y _n ( x ) , для n = 0, 1, 2

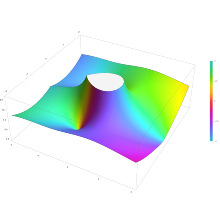
При решении уравнения Гельмгольца в сферических координатах методом разделения переменных радиальное уравнение имеет вид $$x^{2}{\frac {d^{2}y}{dx^{2}}}+2x{\frac {dy}{dx}}+\left(x^{2}-n(n+1)\right)y=0.$$

Два линейно независимых решения этого уравнения называются сферическими функциями Бесселя j _n и y _n и связаны с обычными функциями Бесселя J _n и Y _n соотношением $${\begin{aligned}j_{n}(x)&={\sqrt {\frac {\pi }{2x}}}J_{n+{\frac {1}{2}}}(x),\\y_{n}(x)&={\sqrt {\frac {\pi }{2x}}}Y_{n+{\frac {1}{2}}}(x)=(-1)^{n+1}{\sqrt {\frac {\pi }{2x}}}J_{-n-{\frac {1}{2}}}(x).\end{aligned}}$$

y _n обозначается nn _η или n _; также некоторые авторы называют эти функции сферическими функциями Неймана .

Из связей с обычными функциями Бесселя непосредственно видно, что: $${\begin{aligned}j_{n}(x)&=(-1)^{n}y_{-n-1}(x)\\y_{n}(x)&=(-1)^{n+1}j_{-n-1}(x)\end{aligned}}$$

Сферические функции Бесселя также можно записать в виде ( формулы Рэлея ) $${\begin{aligned}j_{n}(x)&=(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}{\frac {\sin x}{x}},\\y_{n}(x)&=-(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}{\frac {\cos x}{x}}.\end{aligned}}$$

Нулевая сферическая функция Бесселя j ₀ ( x ) также известна как (ненормированная) функция sinc . Первые несколько сферических функций Бесселя: $${\begin{aligned}j_{0}(x)&={\frac {\sin x}{x}}.\\j_{1}(x)&={\frac {\sin x}{x^{2}}}-{\frac {\cos x}{x}},\\j_{2}(x)&=\left({\frac {3}{x^{2}}}-1\right){\frac {\sin x}{x}}-{\frac {3\cos x}{x^{2}}},\\j_{3}(x)&=\left({\frac {15}{x^{3}}}-{\frac {6}{x}}\right){\frac {\sin x}{x}}-\left({\frac {15}{x^{2}}}-1\right){\frac {\cos x}{x}}\end{aligned}}$$и $${\begin{aligned}y_{0}(x)&=-j_{-1}(x)=-{\frac {\cos x}{x}},\\y_{1}(x)&=j_{-2}(x)=-{\frac {\cos x}{x^{2}}}-{\frac {\sin x}{x}},\\y_{2}(x)&=-j_{-3}(x)=\left(-{\frac {3}{x^{2}}}+1\right){\frac {\cos x}{x}}-{\frac {3\sin x}{x^{2}}},\\y_{3}(x)&=j_{-4}(x)=\left(-{\frac {15}{x^{3}}}+{\frac {6}{x}}\right){\frac {\cos x}{x}}-\left({\frac {15}{x^{2}}}-1\right){\frac {\sin x}{x}}.\end{aligned}}$$

Генерирующая функция

Сферические функции Бесселя имеют производящие функции $${\begin{aligned}{\frac {1}{z}}\cos \left({\sqrt {z^{2}-2zt}}\right)&=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}j_{n-1}(z),\\{\frac {1}{z}}\sin \left({\sqrt {z^{2}-2zt}}\right)&=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}y_{n-1}(z).\end{aligned}}$$

Разложения в конечный ряд

В отличие от целочисленных функций Бесселя J _n ( x ), Y _n ( x ) , сферические функции Бесселя j _n ( x ), y _n ( x ) имеют выражение в виде конечного ряда: $${\begin{alignedat}{2}j_{n}(x)&={\frac {\pi }{2x}}J_{n+{\frac {1}{2}}}(x)=\\&={\frac {1}{2x}}\left[e^{ix}\sum _{r=0}^{n}{\frac {i^{r-n-1}(n+r)!}{r!(n-r)!(2x)^{r}}}+e^{-ix}\sum _{r=0}^{n}{\frac {(-i)^{r-n-1}(n+r)!}{r!(n-r)!(2x)^{r}}}\right]\\&={\frac {1}{x}}\left[\sin \left(x-{\frac {n\pi }{2}}\right)\sum _{r=0}^{\left[{\frac {n}{2}}\right]}{\frac {(-1)^{r}(n+2r)!}{(2r)!(n-2r)!(2x)^{2r}}}+\cos \left(x-{\frac {n\pi }{2}}\right)\sum _{r=0}^{\left[{\frac {n-1}{2}}\right]}{\frac {(-1)^{r}(n+2r+1)!}{(2r+1)!(n-2r-1)!(2x)^{2r+1}}}\right]\\y_{n}(x)&=(-1)^{n+1}j_{-n-1}(x)=(-1)^{n+1}{\frac {\pi }{2x}}J_{-\left(n+{\frac {1}{2}}\right)}(x)=\\&={\frac {(-1)^{n+1}}{2x}}\left[e^{ix}\sum _{r=0}^{n}{\frac {i^{r+n}(n+r)!}{r!(n-r)!(2x)^{r}}}+e^{-ix}\sum _{r=0}^{n}{\frac {(-i)^{r+n}(n+r)!}{r!(n-r)!(2x)^{r}}}\right]=\\&={\frac {(-1)^{n+1}}{x}}\left[\cos \left(x-{\frac {n\pi }{2}}\right)\sum _{r=0}^{\left[{\frac {n}{2}}\right]}{\frac {(-1)^{r}(n+2r)!}{(2r)!(n-2r)!(2x)^{2r}}}+\sin \left(x-{\frac {n\pi }{2}}\right)\sum _{r=0}^{\left[{\frac {n-1}{2}}\right]}{\frac {(-1)^{r}(n+2r+1)!}{(2r+1)!(n-2r-1)!(2x)^{2r+1}}}\right]\end{alignedat}}$$

Дифференциальные отношения

В дальнейшем f _n представляет собой любое из j _n , y _n , h ⁽¹⁾
_п , ч ⁽²⁾
_n для n = 0, ±1, ±2, ... $${\begin{aligned}\left({\frac {1}{z}}{\frac {d}{dz}}\right)^{m}\left(z^{n+1}f_{n}(z)\right)&=z^{n-m+1}f_{n-m}(z),\\\left({\frac {1}{z}}{\frac {d}{dz}}\right)^{m}\left(z^{-n}f_{n}(z)\right)&=(-1)^{m}z^{-n-m}f_{n+m}(z).\end{aligned}}$$

Сферические функции Ханкеля: h ⁽¹⁾
_п , ч ⁽²⁾
_н

График сферической функции Ганкеля первого рода h ⁽¹⁾
_n ( x ) с n = -0,5 в комплексной плоскости от −2 − 2 i до 2 + 2 i

График сферической функции Ханкеля второго рода h ⁽²⁾
_n ( x ) с n = −0,5 в комплексной плоскости от −2 − 2 i до 2 + 2 i

Существуют также сферические аналоги функций Ганкеля : $${\begin{aligned}h_{n}^{(1)}(x)&=j_{n}(x)+iy_{n}(x),\\h_{n}^{(2)}(x)&=j_{n}(x)-iy_{n}(x).\end{aligned}}$$

Фактически, существуют простые выражения в замкнутой форме для функций Бесселя полуцелого порядка через стандартные тригонометрические функции и, следовательно, для сферических функций Бесселя. В частности, для неотрицательных целых чисел n : $$h_{n}^{(1)}(x)=(-i)^{n+1}{\frac {e^{ix}}{x}}\sum _{m=0}^{n}{\frac {i^{m}}{m!\,(2x)^{m}}}{\frac {(n+m)!}{(n-m)!}},$$

и ч ⁽²⁾
_n является его комплексно-сопряженным числом (для вещественного x ). Отсюда, например, следует, что j ₀ ( x ) = ⁠ грех Икс / Икс ⁠ и y ₀ ( Икс ) знак равно - ⁠ cos x / x ⁠ и так далее.

Сферические функции Ханкеля появляются в задачах, связанных с распространением сферических волн , например, в мультипольном разложении электромагнитного поля .

Функции Риккати–Бесселя: S _n , C _n , ξ _n , ζ _n

Функции Риккати – Бесселя лишь незначительно отличаются от сферических функций Бесселя: $${\begin{aligned}S_{n}(x)&=xj_{n}(x)={\sqrt {\frac {\pi x}{2}}}J_{n+{\frac {1}{2}}}(x)\\C_{n}(x)&=-xy_{n}(x)=-{\sqrt {\frac {\pi x}{2}}}Y_{n+{\frac {1}{2}}}(x)\\\xi _{n}(x)&=xh_{n}^{(1)}(x)={\sqrt {\frac {\pi x}{2}}}H_{n+{\frac {1}{2}}}^{(1)}(x)=S_{n}(x)-iC_{n}(x)\\\zeta _{n}(x)&=xh_{n}^{(2)}(x)={\sqrt {\frac {\pi x}{2}}}H_{n+{\frac {1}{2}}}^{(2)}(x)=S_{n}(x)+iC_{n}(x)\end{aligned}}$$

Комплексный график функций Риккати–Бесселя Sn от −2 − 2 i до 2 + 2 i

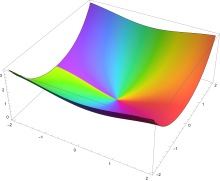
Они удовлетворяют дифференциальному уравнению $$x^{2}{\frac {d^{2}y}{dx^{2}}}+\left(x^{2}-n(n+1)\right)y=0.$$

Например, такого рода дифференциальное уравнение появляется в квантовой механике при решении радиальной составляющей уравнения Шредингера с гипотетическим цилиндрическим бесконечным потенциальным барьером. Это дифференциальное уравнение и решения Риккати-Бесселя также возникают в задаче рассеяния электромагнитных волн сферой, известной как рассеяние Ми после первого опубликованного решения Ми (1908). См., например, Ду (2004). для последних разработок и ссылок.

Следуя Дебаю , обозначения ψn _, Cn χn ₍ используются вместо Sn _, ) иногда ₁₉₀₉ .

Асимптотические формы

Функции Бесселя имеют следующие асимптотики . Для мелких споров $0<z\ll {\sqrt {\alpha +1}}$, получается, когда $\alpha$ не является отрицательным целым числом: $$J_{\alpha }(z)\sim {\frac {1}{\Gamma (\alpha +1)}}\left({\frac {z}{2}}\right)^{\alpha }.$$

Когда α является отрицательным целым числом, мы имеем $$J_{\alpha }(z)\sim {\frac {(-1)^{\alpha }}{(-\alpha )!}}\left({\frac {2}{z}}\right)^{\alpha }.$$

Для функции Бесселя второго рода имеем три случая: $$Y_{\alpha }(z)\sim {\begin{cases}{\dfrac {2}{\pi }}\left(\ln \left({\dfrac {z}{2}}\right)+\gamma \right)&{\text{if }}\alpha =0\\[1ex]-{\dfrac {\Gamma (\alpha )}{\pi }}\left({\dfrac {2}{z}}\right)^{\alpha }+{\dfrac {1}{\Gamma (\alpha +1)}}\left({\dfrac {z}{2}}\right)^{\alpha }\cot(\alpha \pi )&{\text{if }}\alpha {\text{ is a positive integer (one term dominates unless }}\alpha {\text{ is imaginary)}},\\[1ex]-{\dfrac {(-1)^{\alpha }\Gamma (-\alpha )}{\pi }}\left({\dfrac {z}{2}}\right)^{\alpha }&{\text{if }}\alpha {\text{ is a negative integer,}}\end{cases}}$$где γ — постоянная Эйлера–Машерони (0,5772...).

Для больших действительных аргументов z ≫ | α ² − ⁠ 1 / 4 ⁠ | , невозможно написать истинную асимптотическую форму для функций Бесселя первого и второго рода (если только α не является полуцелым ), потому что они имеют нули вплоть до бесконечности, что должно быть точно сопоставлено любым асимптотическим разложением. Однако для заданного значения arg z можно написать уравнение, содержащее член порядка | г | ⁻¹ : $${\begin{aligned}J_{\alpha }(z)&={\sqrt {\frac {2}{\pi z}}}\left(\cos \left(z-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right)+e^{\left|\operatorname {Im} (z)\right|}{\mathcal {O}}\left(|z|^{-1}\right)\right)&&{\text{for }}\left|\arg z\right|<\pi ,\\Y_{\alpha }(z)&={\sqrt {\frac {2}{\pi z}}}\left(\sin \left(z-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right)+e^{\left|\operatorname {Im} (z)\right|}{\mathcal {O}}\left(|z|^{-1}\right)\right)&&{\text{for }}\left|\arg z\right|<\pi .\end{aligned}}$$

( = Для ⁠ 1/2 ⁠ ; последние члены в этих формулах выпадают полностью см. сферические функции Бесселя выше.)

Асимптотические формы функций Ганкеля: $${\begin{aligned}H_{\alpha }^{(1)}(z)&\sim {\sqrt {\frac {2}{\pi z}}}e^{i\left(z-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right)}&&{\text{for }}-\pi <\arg z<2\pi ,\\H_{\alpha }^{(2)}(z)&\sim {\sqrt {\frac {2}{\pi z}}}e^{-i\left(z-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right)}&&{\text{for }}-2\pi <\arg z<\pi .\end{aligned}}$$

Их можно распространить на другие значения arg z, используя уравнения, связывающие H ⁽¹⁾
_α ( так что ^{я π} ) и Ч ⁽²⁾
_α ( так что ^{я π} ) до Ч ⁽¹⁾
_α ( z ) и Ч ⁽²⁾
_α ( z ) .

Интересно, что хотя функция Бесселя первого рода является средним из двух функций Ганкеля, J _α ( z ) не является асимптотической по отношению к среднему из этих двух асимптотических форм, когда z отрицательно (потому что ни одна, ни другая не будет там правильно, в зависимости от используемого аргумента z ). Но асимптотики функций Ханкеля позволяют записать асимптотики функций Бесселя первого и второго рода для комплексных (невещественных) z при условии, что | г | стремится к бесконечности при постоянном фазовом угле arg z (с использованием квадратного корня, имеющего положительную действительную часть): $${\begin{aligned}J_{\alpha }(z)&\sim {\frac {1}{\sqrt {2\pi z}}}e^{i\left(z-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right)}&&{\text{for }}-\pi <\arg z<0,\\[1ex]J_{\alpha }(z)&\sim {\frac {1}{\sqrt {2\pi z}}}e^{-i\left(z-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right)}&&{\text{for }}0<\arg z<\pi ,\\[1ex]Y_{\alpha }(z)&\sim -i{\frac {1}{\sqrt {2\pi z}}}e^{i\left(z-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right)}&&{\text{for }}-\pi <\arg z<0,\\[1ex]Y_{\alpha }(z)&\sim i{\frac {1}{\sqrt {2\pi z}}}e^{-i\left(z-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right)}&&{\text{for }}0<\arg z<\pi .\end{aligned}}$$

Для модифицированных функций Бесселя Ханкель разработал асимптотические (большие аргументы) разложения : также $${\begin{aligned}I_{\alpha }(z)&\sim {\frac {e^{z}}{\sqrt {2\pi z}}}\left(1-{\frac {4\alpha ^{2}-1}{8z}}+{\frac {\left(4\alpha ^{2}-1\right)\left(4\alpha ^{2}-9\right)}{2!(8z)^{2}}}-{\frac {\left(4\alpha ^{2}-1\right)\left(4\alpha ^{2}-9\right)\left(4\alpha ^{2}-25\right)}{3!(8z)^{3}}}+\cdots \right)&&{\text{for }}\left|\arg z\right|<{\frac {\pi }{2}},\\K_{\alpha }(z)&\sim {\sqrt {\frac {\pi }{2z}}}e^{-z}\left(1+{\frac {4\alpha ^{2}-1}{8z}}+{\frac {\left(4\alpha ^{2}-1\right)\left(4\alpha ^{2}-9\right)}{2!(8z)^{2}}}+{\frac {\left(4\alpha ^{2}-1\right)\left(4\alpha ^{2}-9\right)\left(4\alpha ^{2}-25\right)}{3!(8z)^{3}}}+\cdots \right)&&{\text{for }}\left|\arg z\right|<{\frac {3\pi }{2}}.\end{aligned}}$$

Существует также асимптотическая форма (для больших действительных $z$) $${\begin{aligned}I_{\alpha }(z)={\frac {1}{{\sqrt {2\pi z}}{\sqrt[{4}]{1+{\frac {\alpha ^{2}}{z^{2}}}}}}}\exp \left(-\alpha \operatorname {arsinh} \left({\frac {\alpha }{z}}\right)+z{\sqrt {1+{\frac {\alpha ^{2}}{z^{2}}}}}\right)\left(1+{\mathcal {O}}\left({\frac {1}{z{\sqrt {1+{\frac {\alpha ^{2}}{z^{2}}}}}}}\right)\right).\end{aligned}}$$

Когда α = ⁠ 1 / 2 ⁠ , все члены, кроме первого, обращаются в нуль, и мы имеем $${\begin{aligned}I_{{1}/{2}}(z)&={\sqrt {\frac {2}{\pi }}}{\frac {\sinh(z)}{\sqrt {z}}}\sim {\frac {e^{z}}{\sqrt {2\pi z}}}&&{\text{for }}\left|\arg z\right|<{\tfrac {\pi }{2}},\\[1ex]K_{{1}/{2}}(z)&={\sqrt {\frac {\pi }{2}}}{\frac {e^{-z}}{\sqrt {z}}}.\end{aligned}}$$

Для мелких споров $0<|z|\ll {\sqrt {\alpha +1}}$, у нас есть $${\begin{aligned}I_{\alpha }(z)&\sim {\frac {1}{\Gamma (\alpha +1)}}\left({\frac {z}{2}}\right)^{\alpha },\\[1ex]K_{\alpha }(z)&\sim {\begin{cases}-\ln \left({\dfrac {z}{2}}\right)-\gamma &{\text{if }}\alpha =0\\[1ex]{\frac {\Gamma (\alpha )}{2}}\left({\dfrac {2}{z}}\right)^{\alpha }&{\text{if }}\alpha >0\end{cases}}\end{aligned}}$$

Характеристики

Для целочисленного порядка α = n : J _n часто определяется через ряд Лорана для производящей функции $$e^{\left({\frac {x}{2}}\right)\left(t-{\frac {1}{t}}\right)}=\sum _{n=-\infty }^{\infty }J_{n}(x)t^{n}$$подход, использованный П. А. Хансеном в 1843 году. (Этот подход можно обобщить до нецелого порядка путем контурного интегрирования или других методов.)

Бесконечный ряд функций Бесселя в виде ${\textstyle \sum _{\nu =-\infty }^{\infty }J_{N\nu +p}(x)}$ где $\nu ,p,q\in \mathbb {Z} ,\ N\in \mathbb {Z} ^{+}$ возникают во многих физических системах и в замкнутой форме определяются рядом Суна. Например, когда N = 3: ${\textstyle \sum _{\nu =-\infty }^{\infty }J_{3\nu +p}(x)={\frac {1}{3}}\left[1+2\cos {(x{\sqrt {3}}/2-2\pi p/3)}\right]}$. В более общем смысле ряд Сунга и чередующийся ряд Сунга записываются как: $$\sum _{\nu =-\infty }^{\infty }J_{N\nu +p}(x)={\frac {1}{N}}\sum _{q=0}^{N-1}e^{ix\sin {2\pi q/N}}e^{-i2\pi pq/N}$$$$\sum _{\nu =-\infty }^{\infty }(-1)^{\nu }J_{N\nu +p}(x)={\frac {1}{N}}\sum _{q=0}^{N-1}e^{ix\sin {(2q+1)\pi /N}}e^{-i(2q+1)\pi p/N}$$

Разложение в ряд с помощью функций Бесселя ( ряд Каптейна ) имеет вид

${\frac {1}{1-z}}=1+2\sum _{n=1}^{\infty }J_{n}(nz).$

Еще одним важным соотношением для целых порядков является расширение Якоби – Ангера : $$e^{iz\cos \phi }=\sum _{n=-\infty }^{\infty }i^{n}J_{n}(z)e^{in\phi }$$и $$e^{\pm iz\sin \phi }=J_{0}(z)+2\sum _{n=1}^{\infty }J_{2n}(z)\cos(2n\phi )\pm 2i\sum _{n=0}^{\infty }J_{2n+1}(z)\sin((2n+1)\phi )$$который используется для разложения плоской волны как суммы цилиндрических волн или для нахождения ряда Фурье тонально-модулированного FM- сигнала.

В общем, сериал $$f(z)=a_{0}^{\nu }J_{\nu }(z)+2\cdot \sum _{k=1}^{\infty }a_{k}^{\nu }J_{\nu +k}(z)$$называется расширением Неймана f . Коэффициенты при ν = 0 имеют явный вид $$a_{k}^{0}={\frac {1}{2\pi i}}\int _{|z|=c}f(z)O_{k}(z)\,dz$$где O _k — полином Неймана .

Отдельные функции допускают специальное представление $$f(z)=\sum _{k=0}^{\infty }a_{k}^{\nu }J_{\nu +2k}(z)$$с $$a_{k}^{\nu }=2(\nu +2k)\int _{0}^{\infty }f(z){\frac {J_{\nu +2k}(z)}{z}}\,dz$$из-за соотношения ортогональности $$\int _{0}^{\infty }J_{\alpha }(z)J_{\beta }(z){\frac {dz}{z}}={\frac {2}{\pi }}{\frac {\sin \left({\frac {\pi }{2}}(\alpha -\beta )\right)}{\alpha ^{2}-\beta ^{2}}}$$

В более общем смысле, если f имеет точку ветвления вблизи начала координат такой природы, что $$f(z)=\sum _{k=0}a_{k}J_{\nu +k}(z)$$затем $${\mathcal {L}}\left\{\sum _{k=0}a_{k}J_{\nu +k}\right\}(s)={\frac {1}{\sqrt {1+s^{2}}}}\sum _{k=0}{\frac {a_{k}}{\left(s+{\sqrt {1+s^{2}}}\right)^{\nu +k}}}$$или $$\sum _{k=0}a_{k}\xi ^{\nu +k}={\frac {1+\xi ^{2}}{2\xi }}{\mathcal {L}}\{f\}\left({\frac {1-\xi ^{2}}{2\xi }}\right)$$где ${\mathcal {L}}\{f\}$ — преобразование Лапласа функции f .

Другой способ определения функций Бесселя — это формула представления Пуассона и формула Мелера-Сонина: $${\begin{aligned}J_{\nu }(z)&={\frac {\left({\frac {z}{2}}\right)^{\nu }}{\Gamma \left(\nu +{\frac {1}{2}}\right){\sqrt {\pi }}}}\int _{-1}^{1}e^{izs}\left(1-s^{2}\right)^{\nu -{\frac {1}{2}}}\,ds\\[5px]&={\frac {2}{{\left({\frac {z}{2}}\right)}^{\nu }\cdot {\sqrt {\pi }}\cdot \Gamma \left({\frac {1}{2}}-\nu \right)}}\int _{1}^{\infty }{\frac {\sin zu}{\left(u^{2}-1\right)^{\nu +{\frac {1}{2}}}}}\,du\end{aligned}}$$где ν > − ⁠ 1 / 2 ⁠ и z ∈ C . Эта формула особенно полезна при работе с преобразованиями Фурье .

Поскольку уравнение Бесселя становится эрмитовым (самосопряженным), если оно делится на x , решения должны удовлетворять соотношению ортогональности для соответствующих граничных условий. В частности, отсюда следует, что: $$\int _{0}^{1}xJ_{\alpha }\left(xu_{\alpha ,m}\right)J_{\alpha }\left(xu_{\alpha ,n}\right)\,dx={\frac {\delta _{m,n}}{2}}\left[J_{\alpha +1}\left(u_{\alpha ,m}\right)\right]^{2}={\frac {\delta _{m,n}}{2}}\left[J_{\alpha }'\left(u_{\alpha ,m}\right)\right]^{2}$$где α > −1 , δ _{m , n} — дельта Кронекера а u _{α , m} — m -й нуль J α _, ( x ) . Это соотношение ортогональности затем можно использовать для извлечения коэффициентов в ряд Фурье-Бесселя , где функция разлагается по базису функций J _α ( x u _{α , m} ) для фиксированного α и варьирующегося m .

Аналогичное соотношение для сферических функций Бесселя следует сразу: $$\int _{0}^{1}x^{2}j_{\alpha }\left(xu_{\alpha ,m}\right)j_{\alpha }\left(xu_{\alpha ,n}\right)\,dx={\frac {\delta _{m,n}}{2}}\left[j_{\alpha +1}\left(u_{\alpha ,m}\right)\right]^{2}$$

Если определить коробчатую функцию x , которая зависит от малого параметра ε, как: $$f_{\varepsilon }(x)=\varepsilon \operatorname {rect} \left({\frac {x-1}{\varepsilon }}\right)$$(где rect — функция прямоугольника ), то ее преобразование Ханкеля (любого заданного порядка α > − ⁠ 1 / 2 ⁠ ), g _ε ( k ) приближается к J _α ( k ) по мере того, как ε приближается к нулю, для любого заданного k . И наоборот, преобразование Ханкеля (того же порядка) g _ε ( k ) равно f _ε ( x ) : $$\int _{0}^{\infty }kJ_{\alpha }(kx)g_{\varepsilon }(k)\,dk=f_{\varepsilon }(x)$$который равен нулю везде, кроме около 1. Когда ε приближается к нулю, правая часть приближается к δ ( x − 1) , где δ — дельта-функция Дирака . Это допускает предел (в смысле распределения ): $$\int _{0}^{\infty }kJ_{\alpha }(kx)J_{\alpha }(k)\,dk=\delta (x-1)$$

Затем замена переменных дает уравнение замыкания : $$\int _{0}^{\infty }xJ_{\alpha }(ux)J_{\alpha }(vx)\,dx={\frac {1}{u}}\delta (u-v)$$для α > − ⁠ 1/2 ​ ⁠ ​ . Преобразование Ханкеля может выражать довольно произвольную функцию как интеграл от функций Бесселя разных масштабов. Для сферических функций Бесселя соотношение ортогональности имеет вид: $$\int _{0}^{\infty }x^{2}j_{\alpha }(ux)j_{\alpha }(vx)\,dx={\frac {\pi }{2uv}}\delta (u-v)$$для α > −1 .

Другое важное свойство уравнений Бесселя, следующее из тождества Абеля , связано с вронскианом решений: $$A_{\alpha }(x){\frac {dB_{\alpha }}{dx}}-{\frac {dA_{\alpha }}{dx}}B_{\alpha }(x)={\frac {C_{\alpha }}{x}}$$где A _α и B _α — любые два решения уравнения Бесселя, а C _α — константа, не зависящая от x (которая зависит от α и от конкретных рассматриваемых функций Бесселя). В частности, $$J_{\alpha }(x){\frac {dY_{\alpha }}{dx}}-{\frac {dJ_{\alpha }}{dx}}Y_{\alpha }(x)={\frac {2}{\pi x}}$$и $$I_{\alpha }(x){\frac {dK_{\alpha }}{dx}}-{\frac {dI_{\alpha }}{dx}}K_{\alpha }(x)=-{\frac {1}{x}},$$для α > −1 .

При α > −1 четная целая функция рода 1 x ^{− а} J _α ( x ) имеет только действительные нули. Позволять $$0<j_{\alpha ,1}<j_{\alpha ,2}<\cdots <j_{\alpha ,n}<\cdots$$все его положительные нули, тогда $$J_{\alpha }(z)={\frac {\left({\frac {z}{2}}\right)^{\alpha }}{\Gamma (\alpha +1)}}\prod _{n=1}^{\infty }\left(1-{\frac {z^{2}}{j_{\alpha ,n}^{2}}}\right)$$

(Имеется большое количество других известных интегралов и тождеств, которые здесь не воспроизводятся, но которые можно найти в литературе.)

Рекуррентные отношения

Функции J _α , Y _α , H ⁽¹⁾
_α и H ⁽²⁾
_{все α} удовлетворяют рекуррентным соотношениям $${\frac {2\alpha }{x}}Z_{\alpha }(x)=Z_{\alpha -1}(x)+Z_{\alpha +1}(x)$$и $$2{\frac {dZ_{\alpha }(x)}{dx}}=Z_{\alpha -1}(x)-Z_{\alpha +1}(x),$$где Z обозначает J , Y , H ⁽¹⁾ , или Ч ⁽²⁾ . Эти два тождества часто комбинируются, например, складываются или вычитаются, чтобы получить различные другие отношения. Таким образом, например, можно вычислить функции Бесселя более высоких порядков (или более высоких производных) по значениям более низких порядков (или более низких производных). В частности, отсюда следует, что $${\begin{aligned}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{m}\left[x^{\alpha }Z_{\alpha }(x)\right]&=x^{\alpha -m}Z_{\alpha -m}(x),\\\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{m}\left[{\frac {Z_{\alpha }(x)}{x^{\alpha }}}\right]&=(-1)^{m}{\frac {Z_{\alpha +m}(x)}{x^{\alpha +m}}}.\end{aligned}}$$

Модифицированные функции Бесселя подчиняются аналогичным соотношениям: $$e^{\left({\frac {x}{2}}\right)\left(t+{\frac {1}{t}}\right)}=\sum _{n=-\infty }^{\infty }I_{n}(x)t^{n}$$и $$e^{z\cos \theta }=I_{0}(z)+2\sum _{n=1}^{\infty }I_{n}(z)\cos n\theta$$и $${\frac {1}{2\pi }}\int _{0}^{2\pi }e^{z\cos(m\theta )+y\cos \theta }d\theta =I_{0}(z)I_{0}(y)+2\sum _{n=1}^{\infty }I_{n}(z)I_{mn}(y).$$

Рекуррентное соотношение читается $${\begin{aligned}C_{\alpha -1}(x)-C_{\alpha +1}(x)&={\frac {2\alpha }{x}}C_{\alpha }(x),\\[1ex]C_{\alpha -1}(x)+C_{\alpha +1}(x)&=2{\frac {d}{dx}}C_{\alpha }(x),\end{aligned}}$$где C _α обозначает I _α или e ^{ай п} К _α . Эти рекуррентные соотношения полезны для задач дискретной диффузии.

трансцендентность

В 1929 году Карл Людвиг Зигель доказал, что J _ν ( x ) , J ' _ν ( x ) и логарифмическая производная ⁠ J' _ν ( x ) / J _ν ( x ) ⁠ — трансцендентные числа , когда ν рационально, а x алгебраическое и ненулевое. Из того же доказательства также следует, что K _ν ( x ) трансцендентно при тех же предположениях.

Теорема умножения

Функции Бесселя подчиняются теореме умножения $$\lambda ^{-\nu }J_{\nu }(\lambda z)=\sum _{n=0}^{\infty }{\frac {1}{n!}}\left({\frac {\left(1-\lambda ^{2}\right)z}{2}}\right)^{n}J_{\nu +n}(z),$$где λ и ν можно взять как произвольные комплексные числа. Для | л ² − 1 | < 1 , приведенное выше выражение также выполняется, если J заменить на Y . Аналогичные тождества для модифицированных функций Бесселя и | λ ² − 1 | < 1 шт. $$\lambda ^{-\nu }I_{\nu }(\lambda z)=\sum _{n=0}^{\infty }{\frac {1}{n!}}\left({\frac {\left(\lambda ^{2}-1\right)z}{2}}\right)^{n}I_{\nu +n}(z)$$и $$\lambda ^{-\nu }K_{\nu }(\lambda z)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{n!}}\left({\frac {\left(\lambda ^{2}-1\right)z}{2}}\right)^{n}K_{\nu +n}(z).$$

Нули функции Бесселя

Гипотеза Бурже

Сам Бессель первоначально доказал, что для неотрицательных целых чисел n уравнение J _n ( x ) = 0 имеет бесконечное число решений относительно x . Однако когда функции J _n ( x ) изображены на одном и том же графике, ни один из нулей не совпадает для разных значений n, за исключением нуля при x = 0 . Это явление известно как гипотеза Бурже в честь французского математика XIX века, изучавшего функции Бесселя. В частности, он утверждает, что для любых целых чисел n ≥ 0 и m ≥ 1 функции J _n ( x ) и J _{n + m} ( x ) не имеют общих нулей, кроме одного в точке x = 0 . Гипотезу доказал Карл Людвиг Зигель в 1929 году.

трансцендентность

Сигел доказал в 1929 году, что когда рационально , все ненулевые корни J _ν (x) и J ' _ν (x) трансцендентны ν , как и все корни K _ν (x) . Также известно, что все корни высших производных $J_{\nu }^{(n)}(x)$ при n ≤ 18 трансцендентны, за исключением особых значений $J_{1}^{(3)}(\pm {\sqrt {3}})=0$ и $J_{0}^{(4)}(\pm {\sqrt {3}})=0$.

Численные подходы

Численные исследования нулей функции Бесселя см. в Gil, Segura & Temme (2007) , Kravanja et al. (1998) и Молер (2004) .

Числовые значения

Первые нули в J ₀ (т.е. j _0,1 , j _0,2 и j _0,3 ) встречаются при аргументах примерно 2,40483, 5,52008 и 8,65373 соответственно.

См. также

• Функция гнева
• Полиномы Бесселя
• Функция Бесселя – Клиффорда
• Функция Бесселя – Мейтленда
• Ряд Фурье – Бесселя
• Хана – Экстона Бесселя q -функция
• Преобразование Ханкеля
• Неполные функции Бесселя
• Джексона Бесселя q -функция
• Функции Кельвина
• Kontorovich–Lebedev transform
• Алгоритм Ленца
• Правило сумм Лерша – Ньюбергера
• Функция Ломмеля
• Неровный полином
• Полином Неймана
• Функции Риккати-Бесселя.
• Серия Шлёмильха
• Формула Сонина
• Функция Струве
• Колебания круговой мембраны
• Функция Вебера (определенная в функции Гнева )
• Проблема круга Гаусса

Ссылки

• Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964 г.]. «Глава 9» . Справочник по математическим функциям с формулами, графиками и математическими таблицами . Серия «Прикладная математика». Том. 55 (Девятое переиздание с дополнительными исправлениями десятого оригинального издания с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон, округ Колумбия; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Дуврские публикации. стр. 355, 435. ISBN.  978-0-486-61272-0 . LCCN   64-60036 . МР   0167642 . LCCN   65-12253 . См. также главу 10 .
• Арфкен, Джордж Б. и Ханс Дж. Вебер, Математические методы для физиков , 6-е издание (Harcourt: Сан-Диего, 2005). ISBN   0-12-059876-0 .
• Бессель, Фридрих (1824). «Исследование части планетарных возмущений, возникающих из-за движения Солнца». Берлинские трактаты . Воспроизведено на страницах 84–109 в Трактаты Фридриха Вильгельма Бесселя . Лейпциг: Энгельманн. 1875. Английский перевод текста .
• Боуман, Франк «Введение в функции Бесселя» (Дувр: Нью-Йорк, 1958). ISBN   0-486-60462-4 .
• Гил, А.; Сегура, Дж.; Темме, Нью-Мексико (2007). Численные методы для специальных функций . Общество промышленной и прикладной математики.
• Краванья, П. ; Рагос, О.; Врахатис, Миннесота; Зафиропулос, Ф.А. (1998), «ZEBEC: Пакет математического программного обеспечения для вычисления простых нулей функций Бесселя вещественного порядка и комплексного аргумента», Computer Physics Communications , 113 (2–3): 220–238, Бибкод : 1998CoPhC.113. .220K , doi : 10.1016/S0010-4655(98)00064-2
• Ми, Г. (1908). «Вклад в оптику мутных сред, особенно коллоидных растворов металлов» . Анналы физики . 25 (3): 377. Бибкод : 1908АнП...330..377М . дои : 10.1002/andp.19083300302 .
• Олвер, ФВДж ; Максимон, LC (2010), «Функция Бесселя» , в Олвере, Фрэнке В.Дж .; Лозье, Дэниел М.; Буасверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям , издательство Кембриджского университета, ISBN  978-0-521-19225-5 , МР   2723248 ..
• Пресс, WH ; Теукольский, С.А.; Феттерлинг, WT; Фланнери, Б.П. (2007), «Раздел 6.5. Функции Бесселя целочисленного порядка» , Численные рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN  978-0-521-88068-8 , заархивировано из оригинала 03 февраля 2021 г. , получено 28 сентября 2022 г.
• B Испания, М.Г. Смит, Функции математической физики , Van Nostand Reinhold Company, Лондон, 1970. Глава 9 посвящена функциям Бесселя.
• Н. М. Темме, Специальные функции. Введение в классические функции математической физики , John Wiley and Sons, Inc., Нью-Йорк, 1996. ISBN   0-471-11313-1 . Глава 9 посвящена функциям Бесселя.
• Уотсон, Дж. Н. , Трактат по теории функций Бесселя, второе издание , (1995) Издательство Кембриджского университета. ISBN   0-521-48391-3 .
• Вебер, Генрих (1873), «О представлении произвольных функций функциями Бесселя», Mathematical Annals , 6 (2): 146–161, doi : 10.1007/BF01443190 , S2CID   122409461 .

Внешние ссылки

• Лизоркин, П.И. (2001) [1994], «Функции Бесселя» , Энциклопедия Математики , EMS Press .
• Кармазина Л.Н.; Прудников, А.П. (2001) [1994], «Цилиндровая функция» , Энциклопедия Математики , EMS Press .
• Розов, Н.Х. (2001) [1994], «Уравнение Бесселя» , Математическая энциклопедия , EMS Press .
• Страницы функций Wolfram с функциями Бесселя J и Y , а также модифицированными Бесселя I и K. функциями Страницы содержат формулы, средства оценки функций и калькуляторы для построения графиков.
• Вайсштейн, Эрик В. «Функции Бесселя первого рода» . Математический мир .
• Функции Бесселя J _ν , Y _ν , I _ν и K _ν Librow в справочнике Function .
• Ф.В.Дж. Олвер, Л.К. Максимон, Функции Бесселя (глава 10 Цифровой библиотеки математических функций).
• Молер, CB (2004). Численные вычисления с MATLAB (PDF) . Общество промышленной и прикладной математики. Архивировано из оригинала (PDF) 8 августа 2017 г.