Диаграмма Кокстера – Дынкина

Диаграммы Кокстера–Дынкина для фундаментальных конечных групп Кокстера

Диаграммы Кокстера–Дынкина для фундаментальных аффинных групп Кокстера.

В геометрии диаграмма Кокстера - Дынкина построенную (или диаграмма Кокстера , граф Кокстера ) — это граф с пронумерованными ребрами (называемыми ветвями ), представляющий группу Кокстера или иногда однородный многогранник или равномерное мозаику, из группы.

Диаграммы Дынкина — тесно связанные объекты, которые отличаются от диаграмм Кокстера в двух отношениях: во-первых, ветви с пометкой « 4 » или выше являются направленными , тогда как диаграммы Кокстера являются ненаправленными ; во-вторых, диаграммы Дынкина должны удовлетворять дополнительному ( кристаллографическому ) ограничению, а именно, что единственными разрешенными метками ветвей являются 2, 3, 4 и 6. , и используются для их классификации Диаграммы Дынкина соответствуют корневым системам и, следовательно, полупростым алгебрам Ли .

Описание

Группа Кокстера — это группа, которая допускает презентацию: $$\langle r_{0},r_{1},\dots ,r_{n}\mid (r_{i}r_{j})^{m_{i,j}}=1\rangle$$где m _i,j — элементы некоторой симметричной матрицы M которой находится 1 с , на диагонали . Эта матрица M , матрица Кокстера , полностью определяет группу Кокстера.

Поскольку матрица Коксетера симметрична, ее можно рассматривать как матрицу смежности графа, помеченного ребрами , который имеет вершины, соответствующие генераторам r _i , и ребра, помеченные m _i,j между вершинами, соответствующими r _i и r _j . Чтобы упростить эти диаграммы, можно внести два изменения:

• Ребра, помеченные цифрой 2, могут быть опущены, при этом подразумевается, что недостающие ребра равны 2 с. Метка 2 указывает, что соответствующие два генератора коммутируют; 2 — это наименьшее число, которое можно использовать для обозначения ребра.
• Ребра, помеченные цифрой 3, можно оставить без метки, при этом подразумевается, что ребро без метки действует как ребро 3 .

Полученный граф представляет собой диаграмму Кокстера-Дынкина, описывающую рассматриваемую группу Кокстера.

Матрица Шлефли

Каждая диаграмма Коксетера имеет соответствующую матрицу Шлефли (названную так в честь Людвига Шлефли ), A , с матричными элементами a _i,j = a _j,i = −2 cos( π / p _i,j ) , где p _i,j — ветвь порядок между зеркалами i и j ; то есть π / pi _,j — двугранный угол между зеркалами i и j. Как матрица косинусов , A также называется матрицей Грама . Все матрицы Шлефли группы Кокстера симметричны, поскольку их корневые векторы нормализованы. A тесно связана с матрицей Картана , используемой в аналогичном, но ориентированном графе: диаграмме Дынкина в ограниченных случаях p = 2,3,4 и 6, которые обычно не симметричны.

Определитель матрицы Шлефли называется шлефлианом ; Шлефлиан и его знак определяют, является ли группа конечной (положительной), аффинной (нулевой) или неопределенной (отрицательной). Это правило называется критерием Шлефли .

Собственные значения матрицы Шлефли определяют, имеет ли группа Коксетера конечный тип (все положительные), аффинный тип (все неотрицательные, хотя бы один равен нулю) или неопределенный тип (в противном случае). Неопределенный тип иногда подразделяется, например, на гиперболическую и другие группы Кокстера. Однако существует несколько неэквивалентных определений гиперболических групп Кокстера. Мы используем следующие определения:

• Группа Кокстера со связной диаграммой называется гиперболической, если она не имеет ни конечного, ни аффинного типа, но каждая собственная связная поддиаграмма имеет конечный или аффинный тип.
• Гиперболическая группа Кокстера компактна , если все ее подгруппы конечны (т. е. имеют положительные определители), и паракомпактна, если все ее подгруппы конечны или аффинны (т. е. имеют неотрицательные определители).

Конечные и аффинные группы также называются эллиптическими и параболическими соответственно. Гиперболические группы также называются Ланнером в честь Ф. Ланнера, который перечислил компактные гиперболические группы в 1950 году: и Кошул (или квази-Ланнер) для паракомпактных групп.

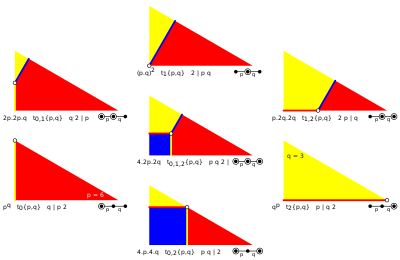
Группы Кокстера 2-го ранга

Тип группы Коксетера ранга 2 , т.е. порожденной двумя разными зеркалами, полностью определяется определителем матрицы Шлефли, поскольку этот определитель является просто произведением собственных значений: конечного (положительный определитель), аффинного (нулевой определитель), или гиперболический (отрицательный определитель) тип. Коксетер использует эквивалентное обозначение скобок , в котором перечислены последовательности порядков ветвей вместо графических диаграмм узлов-ветвлений. Рациональные решения [ p / q ], , также существуют с НОД ( p , q ) = 1; они определяют перекрывающиеся фундаментальные области. Например, 3/2, 4/3, 5/2, 5/3, 5/4 и 6/5.

Тип	Конечный					Аффинный	гиперболический
Геометрия					...
Диаграмма Кокстера Обозначение в скобках	[ ]	[2]	[3]	[4]	[ п ]	[∞]	[∞]	[ип/ л ]
Заказ	2	4	6	8	2 р	∞
Зеркальные линии окрашены в соответствии с узлами диаграммы Коксетера. Фундаментальные домены окрашены попеременно.

showГрупповые диаграммы Кокстера 2-го ранга
Order p	Group	Coxeter diagram		Schläfli matrix
				$\left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]$	Determinant $(4-a_{21}a_{12})$
Finite (Determinant > 0)
2	I2(2) = A1×A1		[2]	$\left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]$	4
3	I2(3) = A2		[3]	$\left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]$	3
3/2			[3/2]	$\left[{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}\right]$
4	I2(4) = B2		[4]	$\left[{\begin{smallmatrix}2&-{\sqrt {2}}\\-{\sqrt {2}}&2\end{smallmatrix}}\right]$	2
4/3			[4/3]	$\left[{\begin{smallmatrix}2&{\sqrt {2}}\\{\sqrt {2}}&2\end{smallmatrix}}\right]$
5	I2(5) = H2		[5]	$\left[{\begin{smallmatrix}2&-\phi \\-\phi &2\end{smallmatrix}}\right]$	$(5-{\sqrt {5}})/2$ ≈ 1.38196601125
5/4			[5/4]	$\left[{\begin{smallmatrix}2&\phi \\\phi &2\end{smallmatrix}}\right]$
5/2			[5/2]	$\left[{\begin{smallmatrix}2&1-\phi \\1-\phi &2\end{smallmatrix}}\right]$	$(5+{\sqrt {5}})/2$ ≈ 3.61803398875
5/3			[5/3]	$\left[{\begin{smallmatrix}2&\phi -1\\\phi -1&2\end{smallmatrix}}\right]$
6	I2(6) = G2		[6]	$\left[{\begin{smallmatrix}2&-{\sqrt {3}}\\-{\sqrt {3}}&2\end{smallmatrix}}\right]$	1
6/5			[6/5]	$\left[{\begin{smallmatrix}2&{\sqrt {3}}\\{\sqrt {3}}&2\end{smallmatrix}}\right]$
8	I2(8)		[8]	$\left[{\begin{smallmatrix}2&-{\sqrt {2+{\sqrt {2}}}}\\-{\sqrt {2+{\sqrt {2}}}}&2\end{smallmatrix}}\right]$	$2-{\sqrt {2}}$ ≈ 0.58578643763
10	I2(10)		[10]	$\left[{\begin{smallmatrix}2&-{\sqrt {(5+{\sqrt {5}})/2}}\\-{\sqrt {(5+{\sqrt {5}})/2}}&2\end{smallmatrix}}\right]$	$(3-{\sqrt {5}})/2$ ≈ 0.38196601125
12	I2(12)		[12]	$\left[{\begin{smallmatrix}2&-{\sqrt {2+{\sqrt {3}}}}\\-{\sqrt {2+{\sqrt {3}}}}&2\end{smallmatrix}}\right]$	$2-{\sqrt {3}}$ ≈ 0.26794919243
p	I2(p)		[p]	$\left[{\begin{smallmatrix}2&-2\cos(\pi /p)\\-2\cos(\pi /p)&2\end{smallmatrix}}\right]$	$4\sin ^{2}(\pi /p)$
Affine (Determinant = 0)
∞	I2(∞) = ${\tilde {I}}_{1}$ = ${\tilde {A}}_{1}$		[∞]	$\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]$	0
Hyperbolic (Determinant ≤ 0)
∞			[∞]	$\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]$	0
∞			[iπ/λ]	$\left[{\begin{smallmatrix}2&-2\cosh(2\lambda )\\-2\cosh(2\lambda )&2\end{smallmatrix}}\right]$	$-4\sinh ^{2}(2\lambda )\leq 0$

Геометрические визуализации

Диаграмму Кокстера – Дынкина можно рассматривать как графическое описание фундаментальной области зеркал. Зеркало представляет собой гиперплоскость внутри сферического, евклидова или гиперболического пространства заданного измерения. (В 2D-пространстве зеркало — это линия; в 3D зеркало — это плоскость.)

Эти визуализации показывают фундаментальные области для 2D- и 3D-евклидовых групп, а также для 2D-сферических групп. Для каждого из них можно вывести диаграмму Кокстера, идентифицировав гиперплоские зеркала и обозначив их связность, игнорируя 90 двугранные углы градусов (порядок 2; см. сноску [a] ниже).

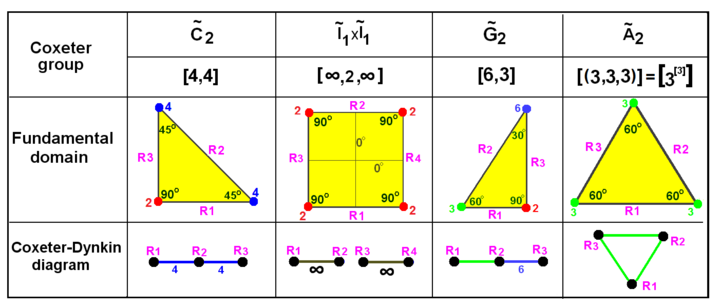Группы Кокстера на евклидовой плоскости с эквивалентными диаграммами. Здесь вершины домена помечены как ветви графа 1, 2 и т. д. и окрашены в соответствии с порядком их отражения (связностью). Отражения помечены как узлы графа R1, R2 и т. д. Отражения под углом 90 градусов неактивны в том смысле, что вместе они не генерируют новых отражений; поэтому они не связаны друг с другом ветвью на схеме. Параллельные зеркала соединены друг с другом ветвью, отмеченной ∞ . Квадрат призматической группы ${\tilde {I}}_{1}$× ${\tilde {I}}_{1}$ отображается как удвоение ${\tilde {C}}_{2}$ треугольник вокруг его стороны R2 *, но также может быть создан в виде прямоугольной области путем удвоения ${\tilde {G}}_{2}$ треугольник вокруг его стороны R2 *. ${\tilde {A}}_{2}$ треугольник представляет собой удвоение ${\tilde {G}}_{2}$ треугольник вокруг его стороны R3 *. *(эта сторона исчезает, удвоившись вокруг себя)
Многие группы Кокстера в гиперболической плоскости могут быть расширены из евклидовых случаев как ряд гиперболических решений.
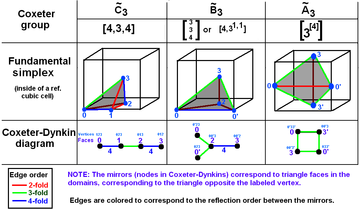Группы Кокстера в трехмерном пространстве с диаграммами. Зеркала (грани треугольника) помечены противоположными вершинами: 0, ..., 3. Ветви раскрашены в соответствии с порядком их отражения. ${\tilde {C}}_{3}$ заполняет 1/48 куба. ${\tilde {B}}_{3}$ заполняет 1/24 куба. ${\tilde {A}}_{3}$ заполняет 1/12 куба.	Группы Кокстера в сфере с эквивалентными диаграммами. Одна фундаментальная область выделена желтым цветом. Вершины домена (и ветви графа) окрашены в соответствии с порядком их отражения.

Приложение к однородным многогранникам

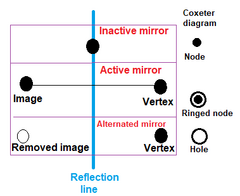При построении однородных многогранников узлы помечаются как активные кольцом, если образующая точка находится за пределами зеркала, создавая новое ребро между образующей точкой и ее зеркальным изображением. Узел без кольца представляет собой неактивное зеркало, которое не генерирует новых точек. Кольцо без узла называется дыркой .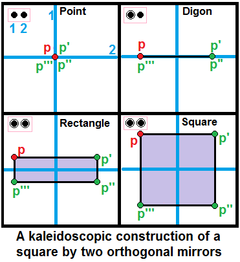

Два ортогональных зеркала можно использовать для создания квадрата. , здесь видно с красной точкой генератора и тремя виртуальными копиями по зеркалам. В этом ортогональном случае генератор должен быть отключен от обоих зеркал, чтобы создать внутреннюю часть. Разметка кольца предполагает, что активные кольца имеют генераторы на одинаковом расстоянии от всех зеркал, а прямоугольник также может представлять собой неоднородное решение.

Диаграммы Коксетера-Динкина могут явно перечислять почти все классы однородных многогранников и однородных мозаик . Каждый однородный многогранник с чистой отражательной симметрией (все, кроме нескольких особых случаев, имеют чистую отражательную симметрию) может быть представлен диаграммой Кокстера-Дынкина с перестановками разметок . Каждый однородный многогранник может быть сгенерирован с использованием таких зеркал и одной точки-генератора: зеркальные изображения создают новые точки в качестве отражений, затем ребра между точками и точкой зеркального изображения можно определить многогранника. Грани генерируются путем многократного отражения края, который в конечном итоге возвращается к исходному генератору; окончательная форма, а также любые грани более высоких измерений также создаются отражением грани, охватывающей область.

Чтобы указать генерирующую вершину, один или несколько узлов помечаются кольцами, что означает, что вершина не находится на зеркале (зеркалах), представленных окольцованным узлом (узлами). (Если отмечено два и более зеркала, вершина равноудалена от них.) Зеркало активно (создает отражения) только по отношению к точкам, не находящимся на нем. Диаграмме необходим хотя бы один активный узел для представления многогранника. Несвязная диаграмма (подгруппы, разделенные ветвями второго порядка или ортогональными зеркалами) требует хотя бы одного активного узла в каждом подграфе.

Все правильные многогранники , представленные символом Шлефли { p , q , r , ...} , могут иметь свои фундаментальные области , представленные набором из n зеркал с соответствующей диаграммой Кокстера-Дынкина линии узлов и ветвей, помеченных p , q , r , ..., с первым узлом, окольцованным.

Однородные многогранники с одним кольцом соответствуют образующим точкам в углах симплекса фундаментальной области. Два кольца соответствуют ребрам симплекса и имеют определенную степень свободы, причем только средняя точка является равномерным решением для ребер одинаковой длины. Обычно k -точки-образующие кольца находятся на (k-1) -гранях симплекса, и если все узлы окольцованы, то образующая точка находится внутри симплекса.

Особый случай однородных многогранников с неотражательной симметрией представлен вторичной разметкой, в которой удалена центральная точка кольцевого узла (называемая дыркой ) . Эти фигуры представляют собой чередования многогранников с отражательной симметрией, что означает, что все остальные вершины удалены. Полученный многогранник будет иметь субсимметрию исходной группы Коксетера . Усеченное чередование называется курносым .

• Один узел представляет собой одно зеркало. Это называется группа _А1 . Если кольцеобразно, это создает сегмент линии , перпендикулярный зеркалу, представленный как {}.
• Два неприсоединенных узла представляют собой два перпендикулярных зеркала. Если оба узла окольцованы, прямоугольник можно создать или квадрат , если точка находится на одинаковом расстоянии от обоих зеркал.
• Два узла, соединенные ветвью порядка n, могут создать n -угольник , если точка находится на одном зеркале, и 2 n -угольник, если точка находится за пределами обоих зеркал. Это образует группу I ₁ (n) .
• Два параллельных зеркала могут представлять бесконечную группу многоугольников I ₁ (∞) , также называемую Ĩ ₁ .
• Три зеркала в треугольнике образуют изображения, видимые в традиционном калейдоскопе , и могут быть представлены тремя узлами, соединенными в треугольник. Повторяющиеся примеры будут иметь ветви, помеченные как (3 3 3), (2 4 4), (2 3 6), хотя последние две можно нарисовать в виде линии (при этом две ветви игнорируются). Это создаст однородные мозаики .
• Три зеркала могут создавать однородные многогранники ; включение рациональных чисел дает набор треугольников Шварца .
• Три зеркала, одно из которых перпендикулярно двум другим, могут образовывать однородные призмы .

Внутри общего треугольника существует 7 отражающих однородных конструкций, основанных на 7 позициях топологических генераторов в фундаментальной области. Каждое активное зеркало генерирует край: два активных зеркала имеют генераторы на сторонах домена, а три активных зеркала имеют генератор внутри. Одну или две степени свободы можно найти в уникальном положении для равных длин ребер полученного многогранника или мозаики.

Пример 7 генераторов на октаэдрической симметрии , фундаментальный треугольник доменов (4 3 2), с 8-м курносым поколением в качестве чередования

Двойники однородных многогранников иногда отмечаются перпендикулярной косой чертой, заменяющей кольцевые узлы, и косой чертой для дырочных узлов курносых. Например, представляет собой прямоугольник (как два активных ортогональных зеркала), а представляет собой двойной многоугольник , ромб .

Примеры с многогранниками и мозаиками

Например, группа B ₃ Кокстера имеет диаграмму: . Это также называется октаэдрической симметрией .

Существует семь выпуклых однородных многогранников , которые можно построить из этой группы симметрии, и три из ее чередующихся подсимметрий, каждый из которых имеет уникально размеченную диаграмму Кокстера – Дынкина. Символ Витхоффа представляет собой особый случай диаграммы Коксетера для графов ранга 3, в котором указаны все три порядка ветвей, а не подавляются ветви второго порядка. Символ Витхоффа способен обрабатывать курносую форму, но не общие чередования без окольцовывания всех узлов.

показывать Однородные октаэдрические многогранники
Symmetry: [4,3], (*432)							[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=				= or	= or	=
Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

Те же конструкции могут быть построены на несвязных (ортогональных) группах Кокстера, таких как однородные призмы , и их можно более четко рассматривать как мозаику диэдров и осоэдров на сфере, как это семейство [6]×[] или [6,2]:

показывать Однородные шестиугольные двугранные сферические многогранники
Symmetry: [6,2], (*622)							[6,2]+, (622)	[6,2+], (2*3)
{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	s{2,6}
Duals to uniforms
V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Для сравнения: [6,3], семейство производит параллельный набор из 7 однородных мозаик евклидовой плоскости и их двойственных мозаик. Опять же 3 чередования и некоторая версия полусимметрии.

показывать Однородные шестиугольные/треугольные плитки
Symmetry: [6,3], (*632)							[6,3]+ (632)	[6,3+] (3*3)
{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}	s{3,6}
63	3.122	(3.6)2	6.6.6	36	3.4.6.4	4.6.12	3.3.3.3.6	3.3.3.3.3.3
Uniform duals
V63	V3.122	V(3.6)2	V63	V36	V3.4.6.4	V.4.6.12	V34.6	V36

В гиперболической плоскости [7,3] семейство производит параллельный набор однородных мозаик и их двойственные мозаики. Существует только 1 чередование ( snub ), поскольку все порядки ветвления нечетные. Многие другие гиперболические семейства однородных мозаик можно увидеть на однородных мозаиках в гиперболической плоскости .

показывать Однородные семиугольные/треугольные мозаики
Symmetry: [7,3], (*732)							[7,3]+, (732)
{7,3}	t{7,3}	r{7,3}	t{3,7}	{3,7}	rr{7,3}	tr{7,3}	sr{7,3}
Uniform duals
V73	V3.14.14	V3.7.3.7	V6.6.7	V37	V3.4.7.4	V4.6.14	V3.3.3.3.7

Очень расширенные диаграммы Кокстера

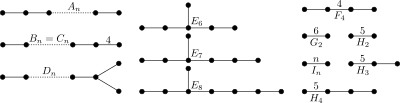
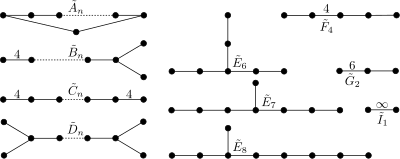
Одно использование включает в себя очень расширенное определение из прямого использования диаграммы Дынкина , которое рассматривает аффинные группы как расширенные , гиперболические группы как чрезмерно расширенные , а третий узел как очень расширенные простые группы. Эти расширения обычно обозначаются показателем степени 1, 2 или 3 + символами количества расширенных узлов. Этот расширяющийся ряд можно расширить назад, последовательно удаляя узлы из одной и той же позиции в графе, хотя процесс останавливается после удаления узла ветвления. Расширенное семейство E8 _и является наиболее часто встречающимся примером, простирающимся назад от E3 _вперед до _E11 .

Процесс расширения может определить ограниченную серию графов Кокстера, которые прогрессируют от конечных к аффинным, гиперболическим и лоренцевым. Определитель матриц Картана определяет, где ряд изменяется от конечного (положительного) до аффинного (нулевого) и гиперболического (отрицательного) и заканчивается лоренцевой группой, содержащей хотя бы одну гиперболическую подгруппу. Некристаллографические группы H _n образуют расширенный ряд, в котором H ₄ расширяется как компактная гиперболическая группа и перерасширяется до лоренцевой группы.

Определителем матрицы Шлефли по рангу являются:

• это ( А ₁ ^н = [2 ^{п -1} ]) = 2 ^н (Конечно для всех n )
• it( А _n = [3 ^{п -1} ]) = n + 1 (конечно для всех n )
• it( B _n = [4,3 ^{п -2} ]) = 2 (конечно для всех n )
• it( D _n = [3 ^{п -3,1,1} ]) = 4 (конечно для всех n )

Определителями матрицы Шлефли в исключительных рядах являются:

• it( E _n = [3 ^{п -3,2,1} ]) = 9 − n (конечный для E ₃ (= A ₂ A ₁ ), E ₄ (= A ₄ ​​), E ₅ (= D ₅ ), E ₆ , E ₇ и E ₈ , аффинный для E ₉ ( ${\tilde {E}}_{8}$), гиперболический при E ₁₀ )
• это([3 ^{п -4,3,1} ]) = 2(8 − n ) (конечный для n = от 4 до 7, аффинный ( ${\tilde {E}}_{7}$) и гиперболический при n = 8.)
• это([3 ^{п -4,2,2} ]) = 3(7 − n ) (конечный для n = от 4 до 6, аффинный ( ${\tilde {E}}_{6}$) и гиперболический при n = 7.)
• it( F _n = [3,4,3 ^{п -3} ]) = 5 − n (конечный для F ₃ (= B ₃ ) по F ₄ , аффинный в F ₅ ( ${\tilde {F}}_{4}$), гиперболический при F ₆ )
• it( G _n = [6,3 ^{п -2} ]) = 3 − n (конечный для G ₂ , аффинный для G ₃ ( ${\tilde {G}}_{2}$), гиперболический в G ₄ )

Меньшая расширенная серия

Конечный	$A_{2}$	$C_{2}$	$G_{2}$	$A_{3}$	$B_{3}$	$C_{3}$	$H_{4}$
Ранг n	[3 [3] ,3 п -3 ]	[4,4,3 п -3 ]	Г н =[6,3 п -2 ]	[3 [4] ,3 п -4 ]	[4,3 1, п −3 ]	[4,3,4,3 п -4 ]	Н н =[5,3 п -2 ]
2	[3] AА2	[4] С 2	[6] Г 2		[2] А 1 2	[4] С 2	[5] Ч 2
3	[3 [3] ] $A_{2}^{+}={\tilde {A}}_{2}$	[4,4] $C_{2}^{+}={\tilde {C}}_{2}$	[6,3] $G_{2}^{+}={\tilde {G}}_{2}$	[3,3]=А 3	[4,3] BБ3	[4,3] С 3	[5,3] HH3
4	[3 [3] ,3] $A_{2}^{++}={\overline {P}}_{3}$	[4,4,3] $C_{2}^{++}={\overline {R}}_{3}$	[6,3,3] $G_{2}^{++}={\overline {V}}_{3}$	[3 [4] ] $A_{3}^{+}={\tilde {A}}_{3}$	[4,3 1,1 ] $B_{3}^{+}={\tilde {B}}_{3}$	[4,3,4] $C_{3}^{+}={\tilde {C}}_{3}$	[5,3,3] Ч 4
5	[3 [3] ,3,3] AА2 +++	[4,4,3,3] С 2 +++	[6,3,3,3] Г 2 +++	[3 [4] ,3] $A_{3}^{++}={\overline {P}}_{4}$	[4,3 2,1 ] $B_{3}^{++}={\overline {S}}_{4}$	[4,3,4,3] $C_{3}^{++}={\overline {R}}_{4}$	[5,3 3 ] Ч 5 = ${\overline {H}}_{4}$
6				[3 [4] ,3,3] AА3 +++	[4,3 3,1 ] BБ3 +++	[4,3,4,3,3] С 3 +++	[5,3 4 ] Ч 6
Это( М н )	3(3− п )	2(3− п )	3− н	4(4− п )	2(4− п )

Средняя расширенная серия

Конечный	$A_{4}$	$B_{4}$	$C_{4}$	$D_{4}$	$F_{4}$	$A_{5}$	$B_{5}$	$D_{5}$
Ранг n	[3 [5] ,3 п -5 ]	[4,3,3 п −4,1 ]	[4,3,3,4,3 п -5 ]	[3 п -4,1,1,1 ]	[3,4,3 п -3 ]	[3 [6] ,3 п -6 ]	[4,3,3,3 п −5,1 ]	[3 1,1 ,3,3 п −5,1 ]
3		[4,3 −1,1 ] Б 2 А 1	[4,3] BБ3	[3 −1,1,1,1 ] А 1 3	[3,4] BБ3		[4,3,3] С 3
4	[3 3 ] A 4	[4,3,3] Б 4	[4,3,3] С 4	[3 0,1,1,1 ] Д 4	[3,4,3] FF4		[4,3,3,3 −1,1 ] Б 3 А 1	[3 1,1 ,3,3 −1,1 ] А 3 А 1
5	[3 [5] ] $A_{4}^{+}={\tilde {A}}_{4}$	[4,3,3 1,1 ] $B_{4}^{+}={\tilde {B}}_{4}$	[4,3,3,4] $C_{4}^{+}={\tilde {C}}_{4}$	[3 1,1,1,1 ] $D_{4}^{+}={\tilde {D}}_{4}$	[3,4,3,3] $F_{4}^{+}={\tilde {F}}_{4}$	[3 4 ] AА5	[4,3,3,3,3] Б 5	[3 1,1 ,3,3] Д 5
6	[3 [5] ,3] $A_{4}^{++}={\overline {P}}_{5}$	[4,3,3 2,1 ] $B_{4}^{++}={\overline {S}}_{5}$	[4,3,3,4,3] $C_{4}^{++}={\overline {R}}_{5}$	[3 2,1,1,1 ] $D_{4}^{++}={\overline {Q}}_{5}$	[3,4,3 3 ] $F_{4}^{++}={\overline {U}}_{5}$	[3 [6] ] $A_{5}^{+}={\tilde {A}}_{5}$	[4,3,3,3 1,1 ] $B_{5}^{+}={\tilde {B}}_{5}$	[3 1,1 ,3,3 1,1 ] $D_{5}^{+}={\tilde {D}}_{5}$
7	[3 [5] ,3,3] A 4 +++	[4,3,3 3,1 ] Б 4 +++	[4,3,3,4,3,3] С 4 +++	[3 3,1,1,1 ] Д 4 +++	[3,4,3 4 ] FF4 +++	[3 [6] ,3] $A_{5}^{++}={\overline {P}}_{6}$	[4,3,3,3 2,1 ] $B_{5}^{++}={\overline {S}}_{6}$	[3 1,1 ,3,3 2,1 ] $D_{5}^{++}={\overline {Q}}_{6}$
8						[3 [6] ,3,3] AА5 +++	[4,3,3,3 3,1 ] Б 5 +++	[3 1,1 ,3,3 3,1 ] Д 5 +++
Это( М н )	5(5− п )	2(5− п )		4(5− п )	5− н	6(6− п )	4(6− п )

Некоторые более высокие расширенные серии

Конечный	$A_{6}$	$B_{6}$	$D_{6}$	$E_{6}$	$A_{7}$	$B_{7}$	$D_{7}$	$E_{7}$	$E_{8}$
Ранг n	[3 [7] ,3 п -7 ]	[4,3 3 ,3 п −6,1 ]	[3 1,1 ,3,3,3 п −6,1 ]	[3 п -5,2,2 ]	[3 [8] ,3 п -8 ]	[4,3 4 ,3 п −7,1 ]	[3 1,1 ,3,3,3,3 п −7,1 ]	[3 п -5,3,1 ]	Е н =[3 п -4,2,1 ]
3									[3 −1,2,1 ] Е 3 =А 2 А 1
4				[3 −1,2,2 ] AА2 2				[3 −1,3,1 ] А 3 А 1	[3 0,2,1 ] Е 4 =А 4
5		[4,3,3,3,3 −1,1 ] Б 4 А 1	[3 1,1 ,3,3,3 −1,1 ] Д 4 А 1	[3 0,2,2 ] AА5				[3 0,3,1 ] AА5	[3 1,2,1 ] Е 5 =Д 5
6	[3 5 ] А 6	[4,3 4 ] Б 6	[3 1,1 ,3,3,3] Д 6	[3 1,2,2 ] EЕ6		[4,3,3,3,3,3 −1,1 ] Б 5 А 1	[3 1,1 ,3,3,3,3 −1,1 ] Д 5 А 1	[3 1,3,1 ] Д 6	[3 2,2,1 ] Е 6 *
7	[3 [7] ] $A_{6}^{+}={\tilde {A}}_{6}$	[4,3 3 ,3 1,1 ] $B_{6}^{+}={\tilde {B}}_{6}$	[3 1,1 ,3,3,3 1,1 ] $D_{6}^{+}={\tilde {D}}_{6}$	[3 2,2,2 ] $E_{6}^{+}={\tilde {E}}_{6}$	[3 6 ] A 7	[4,3 5 ] Б 7	[3 1,1 ,3,3,3,3 0,1 ] D 7	[3 2,3,1 ] E 7 *	[3 3,2,1 ] E 7 *
8	[3 [7] ,3] $A_{6}^{++}={\overline {P}}_{7}$	[4,3 3 ,3 2,1 ] $B_{6}^{++}={\overline {S}}_{7}$	[3 1,1 ,3,3,3 2,1 ] $D_{6}^{++}={\overline {Q}}_{7}$	[3 3,2,2 ] $E_{6}^{++}={\overline {T}}_{7}$	[3 [8] ] $A_{7}^{+}={\tilde {A}}_{7}$ *	[4,3 4 ,3 1,1 ] $B_{7}^{+}={\tilde {B}}_{7}$ *	[3 1,1 ,3,3,3,3 1,1 ] $D_{7}^{+}={\tilde {D}}_{7}$ *	[3 3,3,1 ] $E_{7}^{+}={\tilde {E}}_{7}$ *	[3 4,2,1 ] 8 *
9	[3 [7] ,3,3] А 6 +++	[4,3 3 ,3 3,1 ] Б 6 +++	[3 1,1 ,3,3,3 3,1 ] Д 6 +++	[3 4,2,2 ] EЕ6 +++	[3 [8] ,3] $A_{7}^{++}={\overline {P}}_{8}$ *	[4,3 4 ,3 2,1 ] $B_{7}^{++}={\overline {S}}_{8}$ *	[3 1,1 ,3,3,3,3 2,1 ] $D_{7}^{++}={\overline {Q}}_{8}$ *	[3 4,3,1 ] $E_{7}^{++}={\overline {T}}_{8}$ *	[3 5,2,1 ] Е9 = $E_{8}^{+}={\tilde {E}}_{8}$ *
10					[3 [8] ,3,3] A 7 +++ *	[4,3 4 ,3 3,1 ] Б 7 +++ *	[3 1,1 ,3,3,3,3 3,1 ] D 7 +++ *	[3 5,3,1 ] E 7 +++ *	[3 6,2,1 ] Е 10 = $E_{8}^{++}={\overline {T}}_{9}$ *
11									[3 7,2,1 ] Е 11 = Е 8 +++ *
Это( М н )	7(7− п )	2(7− п )	4(7− п )	3(7− п )	8(8− п )	2(8− п )	4(8− п )	2(8− п )	9− н

Геометрическое складывание

Конечные и аффинные свертки

φ A : A Γ → A Γ' для конечных типов
С	С'	Описание складывания	Диаграммы Кокстера – Дынкина
я 2 ( ч )	С(ч)	Двугранное складывание
Б н	2н ​	(Я, с н )
	Д н+1 , А 2n-1	(А 3 ,±ε)
FF4	EЕ6	(А 3 ,±ε)
Ч 4	E8	(A 4 ,±ε)
HH3	Д 6
Ч 2	A 4
Г 2	AА5	(А 5 ,±ε)
	Д 4	(Д 4 ,±ε)
е: А С + → А С' + для аффинных типов
${\tilde {A}}_{n-1}$	${\tilde {A}}_{kn-1}$	Локально тривиально
${\tilde {B}}_{n}$	${\tilde {D}}_{2n+1}$	(Я, с н )
	${\tilde {D}}_{n+1}$, ${\tilde {D}}_{2n}$	(А 3 ,±ε)
${\tilde {C}}_{n}$	${\tilde {B}}_{n+1}$, ${\tilde {C}}_{2n}$	(А 3 ,±ε)
	${\tilde {C}}_{2n+1}$	(Я, с н )
${\tilde {C}}_{n}$	${\tilde {A}}_{2n+1}$	(I,s n ) & (I,s 0 )
	${\tilde {A}}_{2n}$	(A 3 ,ε) & (I,s 0 )
	${\tilde {A}}_{2n-1}$	(А 3 ,е) и (А 3 ,е')
${\tilde {C}}_{n}$	${\tilde {D}}_{n+2}$	(А 3 ,−ε) & (А 3 ,−ε')
${\tilde {C}}_{2}$	${\tilde {D}}_{5}$	(I, стр. 1 )
${\tilde {F}}_{4}$	${\tilde {E}}_{6}$, ${\tilde {E}}_{7}$	(А 3 ,±ε)
${\tilde {G}}_{2}$	${\tilde {D}}_{6}$, ${\tilde {E}}_{7}$	(А 5 ,±ε)
	${\tilde {B}}_{3}$, ${\tilde {F}}_{4}$	(В 3 ,±ε)
	${\tilde {D}}_{4}$, ${\tilde {E}}_{6}$	(Д 4 ,±ε)

См. Также: Диаграмма Дынкина § Складывание.

Диаграмма Кокстера-Дынкина (с простой связкой) (конечная, аффинная или гиперболическая), имеющая симметрию (удовлетворяющую одному условию, приведенному ниже), может быть факторизована по симметрии, давая новую, обычно многослойную диаграмму, с процессом, называемым « складной».

Например, при _ребро сворачивании D4 в G2 _в G2 _{указывает} из класса трех внешних узлов (валентность 1) на класс центрального узла (валентность 3). И E ₈ складывается в 2 копии H ₄ , вторая копия масштабируется на τ .

Геометрически это соответствует ортогональным проекциям однородных многогранников и мозаик. Примечательно, что любую конечную диаграмму Кокстера–Дынкина с простой связкой можно свернуть в I ₂ ( h ), где h — число Кокстера , которое геометрически соответствует проекции на плоскость Кокстера .

Несколько гиперболических складок

Сложные размышления

Диаграммы Кокстера – Дынкина были расширены на комплексное пространство , C ^н где узлы представляют собой унитарные отражения с периодом больше 2. Узлы помечены индексом, который считается равным 2 для обычного реального отражения, если оно подавлено. Коксетер записывает комплексную группу p[q]r в виде диаграммы .

Одномерный правильный комплексный многогранник в $\mathbb {C} ^{1}$ представлен как , имеющий p вершин. Его реальным представлением является правильный многоугольник { p }. Его симметрия равна _p [] или , заказывайте п . Генератор унитарного оператора для рассматривается как вращение $\mathbb {R} ^{2}$ на 2 π / p радиан против часовой стрелки , и a край создается последовательным применением одного унитарного отражения. Генератор унитарного отражения для 1-многогранника с p вершинами — это e ^{2 π я / п} знак равно потому что (2 π / п ) + я грех (2 π / п ) . Когда p = 2, генератором является e ^{π я} = –1, то же самое, что и отражение точки в реальной плоскости.

В более высоком многограннике _p {} или представляет элемент p -ребра с 2-краем, {} или , представляющий обычное вещественное ребро между двумя вершинами.

Регулярные комплексные 1-многогранники

Комплексные 1-многогранники, , представленные на плоскости Аргана в виде правильных многоугольников для p = 2, 3, 4, 5 и 6, с черными вершинами. Центр тяжести вершин p показан красным. Стороны многоугольников представляют собой одно применение генератора симметрии, сопоставляющее каждую вершину со следующей копией, расположенной против часовой стрелки. Эти многоугольные стороны не являются реберными элементами многогранника, поскольку комплексный 1-многогранник не может иметь ребер (часто это комплексное ребро) и содержит только вершинные элементы.

12 неприводимых групп Шепарда с отношениями индексов их подгрупп. Индекс подгруппы 2 связывается путем удаления реального отражения: п [2 q ] 2 → п [ q ] п , индекс 2. п [4] q → п [ q ] п , индекс q .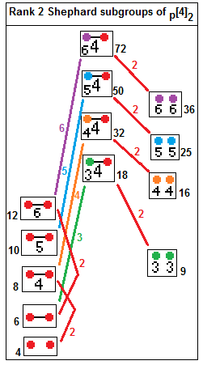

p [4] 2 подгруппы: p=2,3,4... п [4] 2 → [ п ], индекс р p [4] 2 → p [] × p [], индекс 2

Правильный комплексный многоугольник в $\mathbb {C} ^{2}$, имеет вид _p { q } _r или диаграмму Кокстера . Группа симметрии правильного комплексного многоугольника называется не группой Кокстера , а группой Шепарда , типом группы комплексного отражения . Порядок _p [ q ] _r равен $8/q\cdot (1/p+2/q+1/r-1)^{-2}$.

Группы Шепарда ранга 2: ₂ [ q ] ₂ , _p [4] ₂ , ₃ [3] ₃ , ₃ [6] ₂ , ₃ [4] ₃ , ₄ [3] ₄ , ₃ [8] ₂ , ₄ [6] ₂ , ₄ [4] ₃ , ₃ [5] ₃ , ₅ [3] ₅ , ₃ [10] ₂ , ₅ [6] ₂ и ₅ [4] ₃ или , , , , , , , , , , , , , порядка 2 q , 2 p ² , 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200 и 1800 соответственно.

Группа симметрии _{p 1} [ q ] _{p 2} представлена ​​2 образующими R ₁ , R ₂ , где:

Р ₁ ^{п ₁} = _Р2 ^{п ₂} = Я.

Если q четное, (R ₂ R ₁ ) ^{д /2} = (р ₁ р ₂ ) ^{д /2} . Если q нечетно, (R ₂ R ₁ ) ^(q-1)/2 р ₂ = (р ₁ р ₂ ) ^{( q -1)/2} Р ₁ . Когда q нечетно p1 _​ = p2 _, .

The $\mathbb {C} ^{3}$ группа или [1 1 1] ^п определяется тремя унитарными отражениями периода 2 {R ₁ , R ₂ , R ₃ }:

Р ₁ ² = _Р1 ² = Р ₃ ² = (р ₁ р ₂ ) ³ = (р ₂ р ₃ ) ³ = (р ₃ р ₁ ) ³ = (р ₁ р ₂ р ₃ р ₁ ) ^п = 1.

Период p можно рассматривать как двойной оборот в реальном мире. $\mathbb {R} ^{4}$.

Подобный $\mathbb {C} ^{3}$ группа или [1 1 1] ^(п) определяется тремя унитарными отражениями периода 2 {R ₁ , R ₂ , R ₃ }:

Р ₁ ² = _Р1 ² = Р ₃ ² = (р ₁ р ₂ ) ³ = (р ₂ р ₃ ) ³ = (р ₃ р ₁ ) ³ = (р ₁ р ₂ р ₃ р ₂ ) ^п = 1.

См. также

• Группа Коксетера
• Треугольник Шварца
• Тетраэдр Гурса
• Диаграмма Дынкина
• Однородный многогранник
  • Символ Витхоффа
  • Однородный многогранник
  • Список однородных многогранников
  • Список однородных плоских мозаик
  • Равномерный 4-многогранник
  • Выпуклые однородные соты
  • Выпуклые однородные соты в гиперболическом пространстве
• Конструкция Витгофа и символ Витгофа

Дальнейшее чтение

• Джеймс Э. Хамфрис , Группы отражения и группы Кокстера , Кембриджские исследования по высшей математике, 29 (1990)
• Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1] , Googlebooks [2]
  • (Документ 17) Коксетер , Эволюция диаграмм Кокстера-Динкина , [Новые архивы математики 9 (1991) 233-248]
• Коксетер , Красота геометрии: двенадцать эссе , Dover Publications, 1999, ISBN   978-0-486-40919-1 (Глава 3: Конструкция Витхоффа для однородных многогранников)
• Коксетер , Правильные многогранники (1963), Macmillan Company
  • Правильные многогранники , Третье издание, (1973), Дуврское издание, ISBN   0-486-61480-8 (Глава 5: Калейдоскоп и раздел 11.3 Представление в виде графиков)
• HSM Coxeter и WOJ Moser, Генераторы и связи для дискретных групп, 4-е изд., Springer-Verlag, Нью-Йорк, 1980 г.
• Норман Джонсон , Геометрии и преобразования , главы 11,12,13, препринт 2011 г.
• Н. В. Джонсон , Р. Келлерхалс , Дж. Г. Рэтклифф, С. Т. Чанц, Размер гиперболического симплекса Кокстера , Группы преобразований, 1999, Том 4, Выпуск 4, стр. 329–353 [3] [4]
• Норман В. Джонсон и Азия Ивик Вайс Квадратные целые числа и группы Кокстера. Архивировано 26 марта 2023 г. в Wayback Machine PDF Can. Дж. Математика. Том. 51 (6), 1999, стр. 1307–1336.

Внешние ссылки

• Вайсштейн, Эрик В. «Диаграмма Кокстера – Дынкина» . Математический мир .
• Октябрь 1978 года. Дискуссия по истории диаграмм Кокстера, предложенная Кокстером и Дынкиным в Торонто , Канада ; Сборник интервью Юджина Дынкина по математике, Библиотека Корнелльского университета .