1 32 многогранника

3 21		2 31		1 32
Исправлено 3 21			биректифицировано 3 21
Исправлено 2 31			Исправлено 1 32
Ортогональные проекции в E 7 плоскости Кокстера

В 7-мерной 1 геометрии 32 _— это однородный многогранник , построенный из группы E7 .

Его символ Кокстера — 1 ₃₂ , описывающий его разветвляющуюся диаграмму Кокстера-Дынкина с единственным кольцом на конце одной из 1-узловых последовательностей.

Выпрямленный 1 ₃₂ строится по точкам на средних краях 1 ₃₂ .

Эти многогранники являются частью семейства из 127 (2 ⁷ -1) выпуклые однородные многогранники в 7-мерном измерении , состоящие из однородных фасет многогранников и фигур вершин , определяемые всеми перестановками колец в этой диаграмме Кокстера-Динкина : .

многогранник 1_32

1 32
Тип	Равномерный 7-многогранник
Семья	1 k2 многогранник
Символ Шлефли	{3,3 3,2 }
Символ Коксетера	1 32
Диаграмма Кокстера
6-гранный	182: 56 1 22 126 1 31
5-гранный	4284: 756 1 21 1512 1 21 2016 {3 4 }
4-ликий	23688: 4032 {3 3 } 7560 1 11 12096 {3 3 }
Клетки	50400: 20160 {3 2 } 30240 {3 2 }
Лица	40320 {3}
Края	10080
Вершины	576
Вершинная фигура	т 2 {3 5 }
Полигон Петри	Октадекагон
Группа Коксетера	E 7 , [3 3,2,1 ], заказ 2903040
Характеристики	выпуклый

Этот многогранник может замощить 7-мерное пространство с символом 1 ₃₃ и диаграммой Кокстера-Динкина, . Это ячейка Вороного дуального E ₇ ^* решетка .

Альтернативные названия

• Эмануэль Лодевийк Эльте назвал его V ₅₇₆ (из-за 576 вершин) в своем списке полуправильных многогранников 1912 года.
• Коксетер назвал его 1 ₃₂ из-за разветвляющейся диаграммы Кокстера-Дынкина с единственным кольцом на конце 1-узловой ветви.
• Пентаконтигекса-гекатоникозигекса-экзон (аббревиатура lin) - 56-126 граненый полиэксон (Джонатан Бауэрс)

Изображения

плоскости Кокстера Проекции

E7	Е6/Ф4	В7/А6
[18]	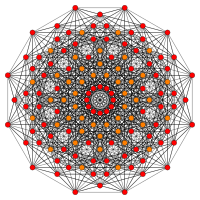[12]	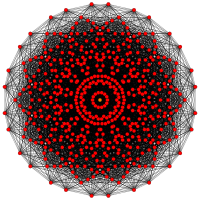[7x2]
А5	D7 / B6	Д6/Б5
[6]	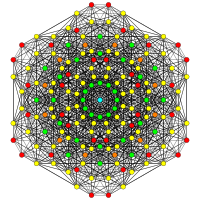[12/2]	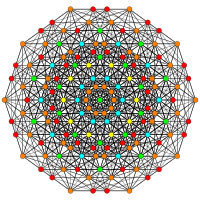[10]
Д5/В4/А4	Д4/Б3/А2/Г2	Д3/Б2/А3
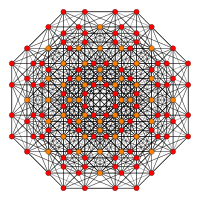[8]	[6]	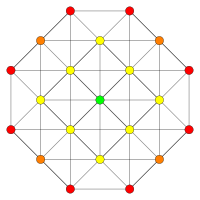[4]

Строительство

Он создан с помощью конструкции Витхоффа на основе набора из 7 гиперплоских зеркал в 7-мерном пространстве.

Информацию о фасетах можно извлечь из диаграммы Кокстера-Динкина .

Удаление узла на конце ветки длиной 2 оставляет 6-полукуб , 1 ₃₁ ,

Удаление узла на конце ветви длиной 3 оставляет 1 ₂₂ ,

Фигура вершины определяется путем удаления окольцованного узла и окольцовывания соседнего узла. Это делает биректифицированный 6-симплекс , 0 ₃₂ ,

В матрице конфигурации количество элементов может быть получено путем удаления зеркал и соотношений групповых порядков Кокстера .

E 7		к -лицо	ж к	ж 0	ж 1	ff2	f 3		ж 4			ж 5			ж 6		к -цифры	примечания
А 6		( )	ж 0	576	35	210	140	210	35	105	105	21	42	21	7	7	2р{3,3,3,3,3}	Е 7 /А 6 = 72*8!/7! = 576
А 3 А 2 А 1		{ }	ж 1	2	10080	12	12	18	4	12	12	6	12	3	4	3	{3,3}x{3}	Е 7 /А 3 А 2 А 1 = 72*8!/4!/3!/2 = 10080
А 2 А 2 А 1		{3}	ff2	3	3	40320	2	3	1	6	3	3	6	1	3	2	{ }∨{3}	Е 7 /А 2 А 2 А 1 = 72*8!/3!/3!/2 = 40320
А 3 А 2		{3,3}	f 3	4	6	4	20160	*	1	3	0	3	3	0	3	1	{3}∨( )	Е 7 /А 3 А 2 = 72*8!/4!/3! = 20160
А 3 А 1 А 1				4	6	4	*	30240	0	2	2	1	4	1	2	2	Филлический дисфеноид	Е 7 /А 3 А 1 А 1 = 72*8!/4!/2/2 = 30240
А 4 А 2		{3,3,3}	ж 4	5	10	10	5	0	4032	*	*	3	0	0	3	0	{3}	Е 7 /А 4 А 2 = 72*8!/5!/3! = 4032
Д 4 А 1		{3,3,4}		8	24	32	8	8	*	7560	*	1	2	0	2	1	{ }∨( )	Е 7 /Д 4 А 1 = 72*8!/8/4!/2 = 7560
А 4 А 1		{3,3,3}		5	10	10	0	5	*	*	12096	0	2	1	1	2		Е 7 /А 4 А 1 = 72*8!/5!/2 = 12096
Д 5 А 1		ч{4,3,3,3}	ж 5	16	80	160	80	40	16	10	0	756	*	*	2	0	{ }	Е 7 /Д 5 А 1 = 72*8!/16/5!/2 = 756
Д 5				16	80	160	40	80	0	10	16	*	1512	*	1	1		Е 7 /Д 5 = 72*8!/16/5! = 1512
А 5 А 1		{3,3,3,3,3}		6	15	20	0	15	0	0	6	*	*	2016	0	2		Е 7 /А 5 А 1 = 72*8!/6!/2 = 2016
EЕ6		{3,3 2,2 }	ж 6	72	720	2160	1080	1080	216	270	216	27	27	0	56	*	( )	Е 7 /Е 6 = 72*8!/72/6! = 56
Д 6		ч{4,3,3,3,3}		32	240	640	160	480	0	60	192	0	12	32	*	126		Е 7 /Д 6 = 72*8!/32/6! = 126

Связанные многогранники и соты

Число 1 ₃₂ является третьим в размерной серии однородных многогранников и сот, выраженной Коксетером 1 _3k как серия . Следующая фигура — это евклидовы соты 1 ₃₃ , а последняя — некомпактные гиперболические соты 1 ₃₄ .

1 _3k- мерные фигуры

Космос	Конечный				евклидов	гиперболический
н	4	5	6	7	8	9
Коксетер группа	А 3 А 1	AА5	Д 6	E 7	${\tilde {E}}_{7}$=E 7 +	${\bar {T}}_{8}$=E 7 ++
Коксетер диаграмма
Симметрия	[3 −1,3,1 ]	[3 0,3,1 ]	[3 1,3,1 ]	[3 2,3,1 ]	[[3 3,3,1 ]]	[3 4,3,1 ]
Заказ	48	720	23,040	2,903,040	∞
График					-	-
Имя	1 3,-1	1 30	1 31	1 32	1 33	1 34

показывать 1 k2 фигур в n измерениях
Space	Finite						Euclidean	Hyperbolic
n	3	4	5	6	7	8	9	10
Coxeter group	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9 = ${\tilde {E}}_{8}$ = E8+	E10 = ${\bar {T}}_{8}$ = E8++
Coxeter diagram
Symmetry (order)	[3−1,2,1]	[30,2,1]	[31,2,1]	[[32,2,1]]	[33,2,1]	[34,2,1]	[35,2,1]	[36,2,1]
Order	12	120	1,920	103,680	2,903,040	696,729,600	∞
Graph							-	-
Name	1−1,2	102	112	122	132	142	152	162

Выпрямленный многогранник 1_32

Исправлено 1 32
Тип	Равномерный 7-многогранник
Символ Шлефли	т 1 {3,3 3,2 }
Символ Коксетера	0 321
Диаграмма Кокстера-Динкина
6-гранный	758
5-гранный	12348
4-ликий	72072
Клетки	191520
Лица	241920
Края	120960
Вершины	10080
Вершинная фигура	{3,3}×{3}×{}
Группа Коксетера	E 7 , [3 3,2,1 ], заказ 2903040
Характеристики	выпуклый

Выпрямленный 1 ₃₂ (также называемый 0 ₃₂₁ ) представляет собой выпрямление многогранника 1 ₃₂ , создающее новые вершины в центре края 1 ₃₂ . Его вершинная фигура представляет собой призму-дуопризму, произведение правильных тетраэдров и треугольника, удвоенного в призму: {3,3}×{3}×{}.

Альтернативные названия

• Выпрямленный пентаконтигекса-гекатоникосигекса-экзон для выпрямленного 56-126 граненого полиэксона (аббревиатура ролин) (Джонатан Бауэрс)

Строительство

Он создан с помощью конструкции Витхоффа на основе набора из 7 гиперплоских зеркал в 7-мерном пространстве. Эти зеркала представлены диаграммой Кокстера-Динкина , , а кольцо представляет положение активного зеркала.

Удаление узла на конце ветви длиной 3 оставляет выпрямленный многогранник 1 ₂₂ ,

Удаление узла на конце ветви длиной 2 оставляет полушестигранник , 1 ₃₁ ,

Удаление узла на конце ветви длиной 1 оставляет биректифицированный 6-симплекс ,

Фигура вершины определяется путем удаления окольцованного узла и окольцовывания соседнего узла. Это делает призму дуопризмы тетраэдра-треугольника {3,3}×{3}×{},

В матрице конфигурации количество элементов может быть получено путем удаления зеркал и соотношений групповых порядков Кокстера .

E 7		к -лицо	ж к	ж 0	ж 1	ff2			f 3					ж 4						ж 5					ж 6			к -цифры	примечания
А 3 А 2 А 1		( )	ж 0	10080	24	24	12	36	8	12	36	18	24	4	12	18	24	12	6	6	8	12	6	3	4	2	3	{3,3}x{3}x{ }	Е 7 /А 3 А 2 А 1 = 72*8!/4!/3!/2 = 10080
А 2 А 1 А 1		{ }	ж 1	2	120960	2	1	3	1	2	6	3	3	1	3	6	6	3	1	3	3	6	2	1	3	1	2	( )v{3}v{ }	Е 7 /А 2 А 1 А 1 = 72*8!/3!/2/2 = 120960
А 2 А 2		0 1	ff2	3	3	80640	*	*	1	1	3	0	0	1	3	3	3	0	0	3	3	3	1	0	3	1	1	{3}v( )v( )	Е 7 /А 2 А 2 = 72*8!/3!/3! = 80640
А 2 А 2 А 1				3	3	*	40320	*	0	2	0	3	0	1	0	6	0	3	0	3	0	6	0	1	3	0	2	{3}v{ }	Е 7 /А 2 А 2 А 1 = 72*8!/3!/3!/2 = 40320
А 2 А 1 А 1				3	3	*	*	120960	0	0	2	1	2	0	1	2	4	2	1	1	2	4	2	1	2	1	2	{ }v{ }v( )	Е 7 /А 2 А 1 А 1 = 72*8!/3!/2/2 = 120960
А 3 А 2		0 2	f 3	4	6	4	0	0	20160	*	*	*	*	1	3	0	0	0	0	3	3	0	0	0	3	1	0	{3}v( )	Е 7 /А 3 А 2 = 72*8!/4!/3! = 20160
		0 11		6	12	4	4	0	*	20160	*	*	*	1	0	3	0	0	0	3	0	3	0	0	3	0	1
А 3 А 1				6	12	4	0	4	*	*	60480	*	*	0	1	1	2	0	0	1	2	2	1	0	2	1	1	клиновидная	Е 7 /А 3 А 1 = 72*8!/4!/2 = 60480
А 3 А 1 А 1				6	12	0	4	4	*	*	*	30240	*	0	0	2	0	2	0	1	0	4	0	1	2	0	2	{ }v{ }	Е 7 /А 3 А 1 А 1 = 72*8!/4!/2/2 = 30240
А 3 А 1		0 2		4	6	0	0	4	*	*	*	*	60480	0	0	0	2	1	1	0	1	2	2	1	1	1	2	клиновидная	Е 7 /А 3 А 1 = 72*8!/4!/2 = 60480
А 4 А 2		0 21	ж 4	10	30	20	10	0	5	5	0	0	0	4032	*	*	*	*	*	3	0	0	0	0	3	0	0	{3}	Е 7 /А 4 А 2 = 72*8!/5!/3! = 4032
А 4 А 1				10	30	20	0	10	5	0	5	0	0	*	12096	*	*	*	*	1	2	0	0	0	2	1	0	{ }v()	Е 7 /А 4 А 1 = 72*8!/5!/2 = 12096
Д 4 А 1		0 111		24	96	32	32	32	0	8	8	8	0	*	*	7560	*	*	*	1	0	2	0	0	2	0	1		Е 7 /Д 4 А 1 = 72*8!/8/4!/2 = 7560
A 4		0 21		10	30	10	0	20	0	0	5	0	5	*	*	*	24192	*	*	0	1	1	1	0	1	1	1	( )v( )v( )	Е 7 /А 4 = 72*8!/5! = 34192
А 4 А 1				10	30	0	10	20	0	0	0	5	5	*	*	*	*	12096	*	0	0	2	0	1	1	0	2	{ }v()	Е 7 /А 4 А 1 = 72*8!/5!/2 = 12096
		0 3		5	10	0	0	10	0	0	0	0	5	*	*	*	*	*	12096	0	0	0	2	1	0	1	2
Д 5 А 1		0 211	ж 5	80	480	320	160	160	80	80	80	40	0	16	16	10	0	0	0	756	*	*	*	*	2	0	0	{ }	Е 7 /Д 5 А 1 = 72*8!/16/5!/2 = 756
AА5		0 22		20	90	60	0	60	15	0	30	0	15	0	6	0	6	0	0	*	4032	*	*	*	1	1	0		Е 7 /А 5 = 72*8!/6! = 4032
Д 5		0 211		80	480	160	160	320	0	40	80	80	80	0	0	10	16	16	0	*	*	1512	*	*	1	0	1		Е 7 /Д 5 = 72*8!/16/5! = 1512
AА5		0 31		15	60	20	0	60	0	0	15	0	30	0	0	0	6	0	6	*	*	*	4032	*	0	1	1		Е 7 /А 5 = 72*8!/6! = 4032
А 5 А 1				15	60	0	20	60	0	0	0	15	30	0	0	0	0	6	6	*	*	*	*	2016	0	0	2		Е 7 /А 5 А 1 = 72*8!/6!/2 = 2016
EЕ6		0 221	ж 6	720	6480	4320	2160	4320	1080	1080	2160	1080	1080	216	432	270	432	216	0	27	72	27	0	0	56	*	*	( )	Е 7 /Е 6 = 72*8!/72/6! = 56
А 6		0 32		35	210	140	0	210	35	0	105	0	105	0	21	0	42	0	21	0	7	0	7	0	*	576	*		Е 7 /А 6 = 72*8!/7! = 576
Д 6		0 311		240	1920	640	640	1920	0	160	480	480	960	0	0	60	192	192	192	0	0	12	32	32	*	*	126		Е 7 /Д 6 = 72*8!/32/6! = 126

Изображения

плоскости Кокстера Проекции

E7	Е6/Ф4	В7/А6
[18]	[12]	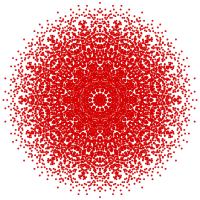[14]
А5	D7 / B6	Д6/Б5
[6]	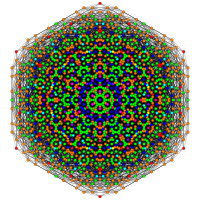[12/2]	[10]
Д5/В4/А4	Д4/Б3/А2/Г2	Д3/Б2/А3
[8]	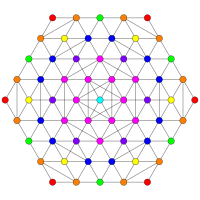[6]	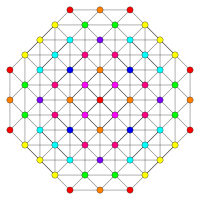[4]

См. также

• Список многогранников E7

Ссылки

• Эльте, EL (1912), Полуправильные многогранники гиперпространств , Гронинген: Гронингенский университет.
• HSM Coxeter , Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
• Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1]
  • (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
• Клитцинг, Ричард. «7D однородные многогранники (полиекса)» . o3o3o3x *c3o3o3o - лин, o3o3x3o *c3o3o3o - ролин