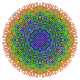
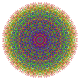
7-демикуб

Демигептеракт (7-демикуб)
многоугольника Петри Проекция
Тип	Равномерный 7-многогранник
Семья	полугиперкуб
Символ Коксетера	1 41
Символ Шлефли	{3,3 4,1 } = ч{4,3 5 } с{2 1,1,1,1,1,1 }
Диаграммы Кокстера	=
6-гранный	78	14 {3 1,3,1 } 64 {3 5 }
5-гранный	532	84 {3 1,2,1 } 448 {3 4 }
4-ликий	1624	280 {3 1,1,1 } 1344 {3 3 }
Клетки	2800	560 {3 1,0,1 } 2240 {3,3}
Лица	2240	{3}
Края	672
Вершины	64
Вершинная фигура	Выпрямленный 6-симплекс
Группа симметрии	D 7 , [3 4,1,1 ] = [1 + ,4,3 5 ] [2 6 ] +
Двойной	?
Характеристики	выпуклый

В геометрии демигептеракт — или 7-демикуб ​​это однородный 7-многогранник , построенный из 7-гиперкуба ( гептеракта ) с удаленными чередующимися вершинами. Он является частью бесконечномерного семейства однородных многогранников, называемых полугиперкубами .

Э. Л. Эльте идентифицировал его в 1912 году как полуправильный многогранник, назвав его HM ₇ для семимерного многогранника половинной меры .

Коксетер назвал этот многогранник как 1 ₄₁ из его диаграммы Кокстера с кольцом на одной из ветвей длины 1, и символ Шлефли $\left\{3{\begin{array}{l}3,3,3,3\\3\end{array}}\right\}$ или {3,3 ^4,1 }.

Декартовы координаты

Декартовы координаты вершин полугептеракта с центром в начале координат представляют собой чередующиеся половины гептеракта :

(±1,±1,±1,±1,±1,±1,±1)

с нечетным количеством знаков плюс.

Изображения

орфографические проекции

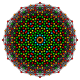
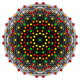
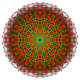
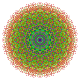
Коксетер самолет	Б 7	D 7	Д 6
График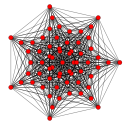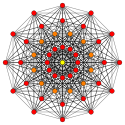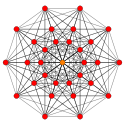
двугранный симметрия	[14/2]	[12]	[10]
Самолет Коксетера	Д 5	Д 4	Д 3
График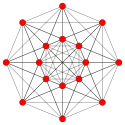
двугранный симметрия	[8]	[6]	[4]
Коксетер самолет	AА5	AА3
График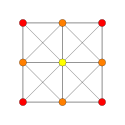
двугранный симметрия	[6]	[4]

В качестве конфигурации

Эта матрица конфигурации представляет собой семикуб. Строки и столбцы соответствуют вершинам, ребрам, граням, ячейкам, 4-граням, 5-граням и 6-граням. Диагональные числа показывают, сколько каждого элемента встречается во всем 7-демикубе. Недиагональные числа показывают, сколько элементов столбца встречается в элементе строки или рядом с ним.

Диагональные числа f-вектора получаются с помощью конструкции Витхоффа , разделяющей полный групповой порядок на подгруппу путем удаления одного зеркала за раз.

D 7		к -лицо	ж к	ж 0	ж 1	ff2	f 3		ж 4		ж 5		ж 6		к -цифры	примечания
А 6		( )	ж 0	64	21	105	35	140	35	105	21	42	7	7	0 41	D 7 /A 6 = 64*7!/7! = 64
А 4 А 1 А 1		{ }	ж 1	2	672	10	5	20	10	20	10	10	5	2	{ }×{3,3,3}	Д 7 /А 4 А 1 А 1 = 64*7!/5!/2/2 = 672
А 3 А 2		1 00	ff2	3	3	2240	1	4	4	6	6	4	4	1	{3,3}v( )	Д 7 /А 3 А 2 = 64*7!/4!/3! = 2240
А 3 А 3		1 01	f 3	4	6	4	560	*	4	0	6	0	4	0	{3,3}	Д 7 /А 3 А 3 = 64*7!/4!/4! = 560
А 3 А 2		1 10		4	6	4	*	2240	1	3	3	3	3	1	{3}v( )	Д 7 /А 3 А 2 = 64*7!/4!/3! = 2240
Д 4 А 2		1 11	ж 4	8	24	32	8	8	280	*	3	0	3	0	{3}	Д 7 /Д 4 А 2 = 64*7!/8/4!/2 = 280
А 4 А 1		1 20		5	10	10	0	5	*	1344	1	2	2	1	{ }v( )	D 7 /A 4 A 1 = 64*7!/5!/2 = 1344
Д 5 А 1		1 21	ж 5	16	80	160	40	80	10	16	84	*	2	0	{ }	D 7 /D 5 A 1 = 64*7!/16/5!/2 = 84
AА5		1 30		6	15	20	0	15	0	6	*	448	1	1		Д 7 /А 5 = 64*7!/6! = 448
Д 6		1 31	ж 6	32	240	640	160	480	60	192	12	32	14	*	( )	Д 7 /Д 6 = 64*7!/32/6! = 14
А 6		1 40		7	21	35	0	35	0	21	0	7	*	64		D 7 /A 6 = 64*7!/7! = 64

Связанные многогранники

Существует 95 однородных многогранников с симметрией D ₆ , 63 имеют общую симметрию B ₆ и 32 уникальны:

Ссылки

• ХСМ Коксетер :
  • Коксетер, Правильные многогранники (3-е издание, 1973 г.), Дуврское издание, ISBN   0-486-61480-8 , с. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерностях (n≥5).
  • HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973, с. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерностях (n≥5).
  • Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1]
    • (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
    • (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
    • (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
• Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN   978-1-56881-220-5 (Глава 26. стр. 409: Гемикубы: 1 _n1 )
• Клитцинг, Ричард. «7D однородные многогранники (polyexa) x3o3o *b3o3o3o3o - hesa» .

Внешние ссылки

• Ольшевский, Георгий. «Демигептеракт» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
• Многомерный глоссарий