Рекуррентная нейронная сеть

Не путать с рекурсивной нейронной сетью .

Рекуррентные нейронные сети (RNN) — это класс искусственных нейронных сетей для последовательной обработки данных. В отличие от нейронных сетей прямого распространения , которые обрабатывают данные за один проход, RNN обрабатывают данные за несколько временных шагов, что делает их хорошо адаптированными для моделирования и обработки текста, речи и временных рядов .

Фундаментальным строительным блоком RNN является рекуррентная единица. Этот блок поддерживает скрытое состояние, по сути, форму памяти, которая обновляется на каждом временном шаге на основе текущего ввода и предыдущего скрытого состояния. Этот цикл обратной связи позволяет сети учиться на прошлых входных данных и включать эти знания в свою текущую обработку.

Ранние RNN страдали от проблемы исчезающего градиента, ограничивавшей их способность изучать долгосрочные зависимости. Проблема была решена благодаря изобретению сетей с длинной краткосрочной памятью (LSTM) в 1997 году, которые стали стандартной архитектурой для RNN.

Они применялись для таких задач, как несегментированное, связанное распознавание рукописного ввода , распознавание речи , обработка естественного языка и нейронный машинный перевод .

История

До ЛСТМ

Одним из источников RNN была статистическая механика . Модель Изинга разработал Вильгельм Ленц. и Эрнст Изинг в 1920-х годах как простая статистико-механическая модель магнитов, находящихся в равновесии. Глаубер в 1963 году изучил модель Изинга, развивающуюся во времени, как процесс достижения равновесия ( динамика Глаубера ), добавив компонент времени. Шуничи Амари в 1972 году предложил изменить веса модели Изинга с помощью правила обучения Хебба как модели ассоциативной памяти, добавив компонент обучения. Ее также называли сетью Хопфилда (1982).

Еще одним источником возникновения RNN стала нейробиология. Слово «рекуррентный» используется для описания петлеобразных структур в анатомии. В 1933 году Лоренте де Но открыл «рекуррентные реципрокные связи» с помощью метода Гольджи и предположил, что возбуждающие петли объясняют определенные аспекты вестибулоокулярного рефлекса . В 1940-х годах несколько человек предположили существование обратной связи в мозге, что контрастировало с предыдущим пониманием нервной системы как структуры исключительно прямой связи. Хебб рассматривал «реверберирующий контур» как объяснение кратковременной памяти. В статье Маккаллоха и Питтса (1943), в которой была предложена модель нейронов Маккаллоха-Питтса , рассматривались сети, содержащие циклы. На текущую деятельность таких сетей может влиять деятельность в неопределенно далеком прошлом. Их обоих интересовали замкнутые циклы как возможные объяснения, например, эпилепсии и каузалгии . Рекуррентное торможение было предложено в 1946 году как механизм отрицательной обратной связи в двигательном контроле. реверберационная схема См. за обширный обзор моделей рекуррентных нейронных сетей в нейробиологии.

Двумя ранними влиятельными работами были сеть Джордана (1986) и сеть Элмана (1990), которые применили RNN для изучения когнитивной психологии . В 1993 году система сжатия нейронной истории решила задачу «очень глубокого обучения», которая требовала более 1000 последующих слоев в RNN, развернутой во времени.

ЛСТМ

Сети с длинной краткосрочной памятью (LSTM) были изобретены Хохрайтером и Шмидхубером в 1997 году и установили рекорды точности во многих областях применения. Он стал выбором по умолчанию для архитектуры RNN.

Примерно в 2007 году LSTM начал производить революцию в распознавании речи , превосходя традиционные модели в некоторых речевых приложениях. В 2009 году сеть LSTM, обученная коннекционистской временной классификации (CTC), стала первой сетью RNN, выигравшей конкурсы по распознаванию образов, когда она выиграла несколько соревнований по связанному распознаванию рукописного ввода . В 2014 году китайская компания Baidu использовала RNN, обученные CTC, для взлома набора данных распознавания речи 2S09 Switchboard Hub5'00. эталонный тест без использования каких-либо традиционных методов обработки речи.

LSTM также улучшил распознавание речи с большим словарным запасом. и текста в речь синтез и использовался в Google Android . Сообщается, что в 2015 году производительность системы распознавания речи Google резко выросла на 49%. через LSTM, обученный CTC.

LSTM побил рекорды по улучшению машинного перевода , Языковое моделирование и многоязычная языковая обработка. LSTM в сочетании со сверточными нейронными сетями (CNN) улучшили автоматическое создание подписей к изображениям .

Конфигурации

Основная статья: Слой (глубокое обучение)

Модель на основе RNN можно разделить на две части: конфигурацию и архитектуру. Несколько RNN могут быть объединены в поток данных, а сам поток данных является конфигурацией. Сама каждая RNN может иметь любую архитектуру, включая LSTM, GRU и т.д.

Стандартный

Сжатая (слева) и развернутая (справа) базовая рекуррентная нейронная сеть

RNN существуют во многих вариантах. Говоря абстрактно, RNN — это функция $f_{\theta }$ типа $(x_{t},h_{t})\mapsto (y_{t},h_{t+1})$, где

• $x_{t}$: входной вектор;
• $h_{t}$: скрытый вектор;
• $y_{t}$: выходной вектор;
• $\theta$: параметры нейронной сети.

Проще говоря, это нейронная сеть, которая отображает входные данные. $x_{t}$ в вывод $y_{t}$, со скрытым вектором $h_{t}$ играющий роль «памяти», частичной записи всех предыдущих пар ввода-вывода. На каждом этапе он преобразует входные данные в выходные и изменяет свою «память», чтобы лучше выполнять будущую обработку.

Иллюстрация справа может ввести многих в заблуждение, поскольку практические топологии нейронных сетей часто организованы в «слои», и на рисунке именно такой вид и создается. Однако то, что кажется слоями , на самом деле представляет собой различные этапы во времени, «развернутые» для создания видимости слоев .

Сложенный RNN

Сложенный RNN.

Составная RNN, или глубокая RNN, состоит из нескольких RNN, расположенных друг над другом. Абстрактно это структурировано следующим образом.

1. Слой 1 имеет скрытый вектор $h_{1,t}$, параметры $\theta _{1}$и карты $f_{\theta _{1}}:(x_{0,t},h_{1,t})\mapsto (x_{1,t},h_{1,t+1})$.
2. Слой 2 имеет скрытый вектор $h_{2,t}$, параметры $\theta _{2}$и карты $f_{\theta _{2}}:(x_{1,t},h_{2,t})\mapsto (x_{2,t},h_{2,t+1})$.
3. ...
4. Слой $n$ имеет скрытый вектор $h_{n,t}$, параметры $\theta _{n}$и карты $f_{\theta _{n}}:(x_{n-1,t},h_{n,t})\mapsto (x_{n,t},h_{n,t+1})$.

Каждый уровень работает как автономная RNN, а выходная последовательность каждого уровня используется в качестве входной последовательности для слоя выше. Высота RNN не ограничена.

Двунаправленный

Основная статья: Двунаправленные рекуррентные нейронные сети

Двунаправленный РНС.

Двунаправленная RNN состоит из двух RNN, одна из которых обрабатывает входную последовательность в одном направлении, а другая — в противоположном. Абстрактно он структурирован следующим образом:

• Прямой RNN обрабатывает в одном направлении: $$f_{\theta }(x_{0},h_{0})=(y_{0},h_{1}),f_{\theta }(x_{1},h_{1})=(y_{1},h_{2}),\dots$$
• Обратный RNN выполняет процессы в противоположном направлении: $$f'_{\theta '}(x_{N},h_{N}')=(y'_{N},h_{N-1}'),f'_{\theta '}(x_{N-1},h_{N-1}')=(y'_{N-1},h_{N-2}'),\dots$$

Затем две выходные последовательности объединяются, чтобы получить общий результат: $((y_{0},y_{0}'),(y_{1},y_{1}'),\dots ,(y_{N},y_{N}'))$.

Двунаправленный RNN позволяет модели обрабатывать токен как в контексте того, что было до него, так и в контексте того, что было после него. Объединив несколько двунаправленных RNN вместе, модель может обрабатывать токен все более контекстуально. Модель ELMo (2018) представляет собой сложенный двунаправленный LSTM , который принимает на входе уровень символов и создает встраивания на уровне слов.

Кодер-декодер

Основная статья: seq2seq

Кодер-декодер RNN без механизма внимания.

Кодер-декодер RNN с механизмом внимания.

Два RNN могут работать последовательно в конфигурации кодер-декодер. Кодер RNN преобразует входную последовательность в последовательность скрытых векторов, а декодер RNN преобразует последовательность скрытых векторов в выходную последовательность с дополнительным механизмом внимания . В период с 2014 по 2017 год это использовалось для создания современных нейронных машинных переводчиков. Это стало важным шагом на пути к разработке трансформеров .

ПиксельRNN

RNN может обрабатывать данные более чем с одним измерением. PixelRNN обрабатывает двумерные данные во многих возможных направлениях. Например, построчное направление обрабатывает $n\times n$ сетка векторов $x_{i,j}$ в следующем порядке: $$x_{1,1},x_{1,2},\dots ,x_{1,n},x_{2,1},x_{2,2},\dots ,x_{2,n},\dots ,x_{n,n}$$Диагональный BiLSTM использует два LSTM для обработки одной и той же сетки. Его обрабатывают из верхнего левого угла в правый нижний, так что он обрабатывает $x_{i,j}$ в зависимости от его скрытого состояния и состояния ячейки сверху и слева: $h_{i-1,j},c_{i-1,j}$ и $h_{i,j-1},c_{i,j-1}$. Другой обрабатывает его из правого верхнего угла в левый нижний.

Архитектуры

Полностью рецидивирующий

Полносвязная RNN с 4 нейронами.

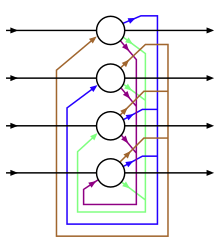
Полностью рекуррентные нейронные сети (FRNN) соединяют выходы всех нейронов со входами всех нейронов. Другими словами, это полностью подключенная сеть . Это наиболее общая топология нейронной сети, поскольку все остальные топологии можно представить, установив для некоторых весов соединений нулевое значение, чтобы имитировать отсутствие связей между этими нейронами.

Простая сеть Элмана, в которой $\sigma _{h}=\tanh ,\sigma _{y}={\text{Identity}}$.

Хопфилд

Основная статья: Сеть Хопфилда

Сеть Хопфилда — это RNN, в которой все соединения между уровнями имеют одинаковый размер. Он требует стационарных входных данных и, следовательно, не является общей RNN, поскольку не обрабатывает последовательности шаблонов. Однако это гарантирует, что оно сойдется. Если соединения обучаются с использованием обучения Хебба , то сеть Хопфилда может работать как надежная память с адресацией по содержимому , устойчивая к изменению соединения.

Сети Элмана и сети Джордана

Сеть Элман

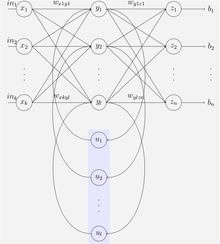
Сеть Элмана — это трехслойная сеть (расположенная горизонтально как x , y и z на рисунке) с добавлением набора контекстных единиц ( u на рисунке). Средний (скрытый) уровень связан с этими единицами контекста, имеющими вес, равный единице. На каждом временном шаге входные данные передаются вперед и правило обучения применяется . Фиксированные обратные соединения сохраняют копию предыдущих значений скрытых модулей в модулях контекста (поскольку они распространяются по соединениям до применения правила обучения). Таким образом, сеть может поддерживать своего рода состояние, позволяющее ей выполнять такие задачи, как прогнозирование последовательности, которые выходят за рамки возможностей стандартного многослойного перцептрона .

Сети Джордана аналогичны сетям Элмана. Единицы контекста подаются из выходного слоя, а не из скрытого слоя. Единицы контекста в сети Иордании также называются уровнем состояния. У них есть постоянная связь с самим собой.

Сети Элмана и Джордана также известны как «Простые рекуррентные сети» (SRN).

Сеть Элмана

${\begin{aligned}h_{t}&=\sigma _{h}(W_{h}x_{t}+U_{h}h_{t-1}+b_{h})\\y_{t}&=\sigma _{y}(W_{y}h_{t}+b_{y})\end{aligned}}$

Иорданская сеть

${\begin{aligned}h_{t}&=\sigma _{h}(W_{h}x_{t}+U_{h}y_{t-1}+b_{h})\\y_{t}&=\sigma _{y}(W_{y}h_{t}+b_{y})\end{aligned}}$

Переменные и функции

• $x_{t}$: входной вектор
• $h_{t}$: вектор скрытого слоя
• $y_{t}$: выходной вектор
• $W$, $U$ и $b$: матрицы параметров и вектор
• $\sigma _{h}$ и $\sigma _{y}$: Функции активации

Длинная кратковременная память

Основная статья: Длинная кратковременная память

Блок долговременной кратковременной памяти

Долговременная краткосрочная память (LSTM) является наиболее широко используемой архитектурой RNN. Он был разработан для решения проблемы исчезающего градиента. LSTM обычно дополняется повторяющимися воротами, называемыми «воротами забывания». LSTM предотвращает исчезновение или взрывной рост ошибок обратного распространения ошибки. Вместо этого ошибки могут течь назад через неограниченное количество виртуальных слоев, развернутых в пространстве. То есть LSTM может изучать задачи которые требуют воспоминаний о событиях, произошедших на тысячи или даже миллионы дискретных временных шагов ранее. Топологии, подобные LSTM, могут быть разработаны для конкретных задач. LSTM работает даже при длительных задержках между важными событиями и может обрабатывать сигналы, в которых смешаны низкочастотные и высокочастотные компоненты.

Многие приложения используют стеки LSTM RNN. и обучать их с помощью коннекционистской временной классификации (CTC) найти весовую матрицу RNN, которая максимизирует вероятность последовательностей меток в обучающем наборе, учитывая соответствующие входные последовательности. CTC достигает как согласованности, так и признания.

LSTM может научиться распознавать контекстно-зависимые языки в отличие от предыдущих моделей, основанных на скрытых моделях Маркова (HMM) и подобных концепциях.

Закрытый рекуррентный блок

Основная статья: Закрытая рекуррентная единица

Закрытый рекуррентный блок

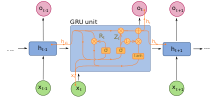
Закрытый рекуррентный блок (GRU), представленный в 2014 году, был разработан как упрощение LSTM. Они используются в полной форме и в нескольких более упрощенных вариантах. У них меньше параметров, чем у LSTM, так как у них нет выходного вентиля.

Было обнаружено, что их эффективность при моделировании полифонической музыки и речевых сигналов аналогична эффективности долговременной кратковременной памяти. Особой разницы в производительности между LSTM и GRU не наблюдается.

Двунаправленная ассоциативная память

Основная статья: Двунаправленная ассоциативная память

Представлено Бартом Коско, Сеть двунаправленной ассоциативной памяти (BAM) — это вариант сети Хопфилда, в которой ассоциативные данные хранятся в виде вектора. Двунаправленность возникает в результате передачи информации через матрицу и ее транспонирования . Обычно биполярное кодирование предпочтительнее двоичного кодирования ассоциативных пар. Недавно стохастические модели BAM, использующие степпинг Маркова, были оптимизированы для повышения стабильности сети и соответствия реальным приложениям.

Сеть BAM имеет два уровня, каждый из которых может использоваться в качестве входных данных для вызова ассоциации и создания выходных данных на другом уровне.

Состояние эха

Основная статья: Государственная сеть «Эхо»

Сети состояний эха (ESN) имеют редко связанный случайный скрытый слой. Веса выходных нейронов — единственная часть сети, которая может изменяться (обучаться). ESN хорошо воспроизводят определенные временные ряды . Вариант импульсных нейронов известен как машина с жидким состоянием .

Рекурсивный

Основная статья: Рекурсивная нейронная сеть

Рекурсивная нейронная сеть создается путем рекурсивного применения одного и того же набора весов к дифференцируемой графоподобной структуре путем обхода структуры в топологическом порядке . Такие сети обычно также обучаются с помощью обратного режима автоматического дифференцирования . Они могут обрабатывать распределенные представления структуры, такие как логические термины . Частным случаем рекурсивных нейронных сетей являются RNN, структура которых соответствует линейной цепочке. Рекурсивные нейронные сети применяются для обработки естественного языка . Рекурсивная нейронная тензорная сеть использует тензорную функцию композиции для всех узлов дерева.

Нейронные машины Тьюринга

Основные статьи: Нейронная машина Тьюринга и дифференцируемый нейронный компьютер

Нейронные машины Тьюринга (НТМ) — это метод расширения рекуррентных нейронных сетей путем подключения их к ресурсам внешней памяти, с которыми они взаимодействуют. Комбинированная система аналогична машине Тьюринга или архитектуре фон Неймана, но является дифференцируемой сквозной , что позволяет эффективно обучать ее с помощью градиентного спуска .

Дифференцируемые нейронные компьютеры (ДНК) являются расширением нейронных машин Тьюринга, позволяющим использовать нечеткие количества каждого адреса памяти и запись хронологии.

Автоматы с выталкиванием нейронной сети (NNPDA) похожи на NTM, но ленты заменены аналоговыми стеками, которые дифференцируются и обучаются. В этом смысле они по сложности аналогичны распознавателям контекстно-свободных грамматик (CFG).

Рекуррентные нейронные сети являются полными по Тьюрингу и могут запускать произвольные программы для обработки произвольных последовательностей входных данных.

Другие архитектуры

Самостоятельно РНН (ИндРНН)

Независимая рекуррентная нейронная сеть (IndRNN) решает проблемы исчезновения и взрыва градиента в традиционной полностью связной RNN. Каждый нейрон в одном слое получает только свое прошлое состояние в качестве контекстной информации (вместо полной связи со всеми другими нейронами в этом слое), и, таким образом, нейроны независимы от истории друг друга. Обратное распространение градиента можно регулировать, чтобы избежать исчезновения и взрыва градиента, чтобы сохранить долговременную или краткосрочную память. Информация о перекрестных нейронах исследуется на следующих уровнях. IndRNN можно надежно обучить с помощью ненасыщенных нелинейных функций, таких как ReLU. Глубокие сети можно обучать, используя пропущенные соединения.

Компрессор нейронной истории

Компрессор нейронной истории представляет собой неконтролируемый набор RNN. На уровне ввода он учится прогнозировать следующий ввод на основе предыдущих входных данных. Только непредсказуемые входные данные некоторых RNN в иерархии становятся входными данными для RNN следующего более высокого уровня, который, следовательно, лишь изредка пересчитывает свое внутреннее состояние. Таким образом, каждая RNN более высокого уровня изучает сжатое представление информации в расположенной ниже RNN. Это делается для того, чтобы входную последовательность можно было точно восстановить по представлению на самом высоком уровне.

Система эффективно минимизирует длину описания или отрицательный логарифм вероятности данных. Учитывая большую предсказуемость входящей последовательности данных, RNN самого высокого уровня может использовать контролируемое обучение, чтобы легко классифицировать даже глубокие последовательности с длинными интервалами между важными событиями.

Иерархию RNN можно разделить на две RNN: «сознательный» блокировщик (более высокий уровень) и «подсознательный» автоматизатор (нижний уровень). Как только блокировщик научится предсказывать и сжимать входные данные, которые непредсказуемы для автоматизатора, автоматизатор может быть вынужден на следующем этапе обучения предсказывать или имитировать с помощью дополнительных блоков скрытые блоки более медленно меняющегося блокатора. Это позволяет автоматизатору легко запоминать подходящие, редко меняющиеся воспоминания на протяжении длительных интервалов времени. В свою очередь, это помогает автоматизатору сделать многие из некогда непредсказуемых входных данных предсказуемыми, так что блокировщик может сосредоточиться на оставшихся непредсказуемых событиях.

Генеративная модель частично решила проблему исчезновения градиента или автоматического дифференцирования обратного распространения ошибки в нейронных сетях в 1992 году. В 1993 году такая система решила задачу «очень глубокого обучения», которая требовала более 1000 последующих слоев в RNN, развернутой во времени.

РНС второго порядка

RNN второго порядка используют веса более высокого порядка. $w{}_{ijk}$ вместо стандартного $w{}_{ij}$ веса и состояния могут быть продуктом. Это позволяет напрямую отображать конечный автомат как при обучении, так и при стабильности и представлении. Длинная кратковременная память является примером этого, но не имеет таких формальных отображений или доказательств стабильности.

Иерархическая рекуррентная нейронная сеть

Иерархические рекуррентные нейронные сети (HRNN) соединяют свои нейроны различными способами, чтобы разложить иерархическое поведение на полезные подпрограммы. Такие иерархические структуры познания присутствуют в теориях памяти, представленных философом Анри Бергсоном , чьи философские взгляды вдохновили на создание иерархических моделей.

Иерархические рекуррентные нейронные сети полезны при прогнозировании , помогая прогнозировать дезагрегированные инфляционные компоненты индекса потребительских цен (ИПЦ). Модель HRNN использует информацию с более высоких уровней иерархии ИПЦ для улучшения прогнозов на более низком уровне. Оценка значительного набора данных по индексу CPI-U в США демонстрирует превосходную эффективность модели HRNN по сравнению с различными признанными методами прогнозирования инфляции .

Рекуррентная многослойная сеть перцептрона

Как правило, рекуррентная многоуровневая сеть перцептрона (сеть RMLP) состоит из каскадных подсетей, каждая из которых содержит несколько уровней узлов. Каждая подсеть является прямой, за исключением последнего уровня, который может иметь соединения обратной связи. Каждая из этих подсетей соединена только прямыми соединениями.

Модель с несколькими временными масштабами

Рекуррентная нейронная сеть с несколькими временными масштабами (MTRNN) — это вычислительная модель на основе нейронов, которая может моделировать функциональную иерархию мозга посредством самоорганизации в зависимости от пространственной связи между нейронами и от различных типов активности нейронов, каждый из которых имеет разные временные свойства. При такой разнообразной активности нейронов непрерывные последовательности любого набора действий сегментируются на многократно используемые примитивы, которые, в свою очередь, гибко интегрируются в различные последовательные модели поведения. Биологическое одобрение такого типа иерархии обсуждалось в теории прогнозирования функций мозга Хокинсом в его книге «Об интеллекте» . Такая иерархия также согласуется с теориями памяти, выдвинутыми философом Анри Бергсоном , которые были включены в модель MTRNN.

Мемристивные сети

Грег Снайдер из HP Labs описывает систему корковых вычислений с использованием мемристивных наноустройств. Мемристоры . (резисторы памяти) выполнены из тонкопленочных материалов, сопротивление которых электрически настраивается за счет транспорта ионов или кислородных вакансий внутри пленки DARPA Проект SyNAPSE профинансировал исследования IBM и лаборатории HP в сотрудничестве с факультетом когнитивных и нейронных систем (CNS) Бостонского университета для разработки нейроморфных архитектур, которые могут быть основаны на мемристивных системах. Мемристивные сети — это особый тип физической нейронной сети , свойства которой очень похожи на сети (Литтла) Хопфилда, поскольку они имеют непрерывную динамику, ограниченный объем памяти и естественную релаксацию посредством минимизации функции, которая асимптотична модели Изинга . В этом смысле динамика мемристивной схемы имеет преимущество по сравнению с сетью резистор-конденсатор, поскольку имеет более интересное нелинейное поведение. С этой точки зрения инженерные аналоговые мемристивные сети представляют собой своеобразный тип нейроморфной инженерии , в котором поведение устройства зависит от схемы подключения или топологии. Эволюцию этих сетей можно изучать аналитически, используя вариации Уравнение Каравелли – Траверсы – Ди Вентры .

Псевдокод

Учитывая временной ряд x длины sequence_length. В рекуррентной нейронной сети есть цикл, обрабатывающий все записи временного ряда. x через слои neural_network один за другим. Они имеют возвращаемое значение на каждом временном шаге. i оба предсказания y_pred[i] и обновленное скрытое состояние hidden, который имеет длину hidden_size. В результате после цикла сбор всех прогнозов y_pred возвращается. Следующий псевдокод (на основе языка программирования Python ) иллюстрирует функциональность рекуррентной нейронной сети.

def RNN_forward(x, sequence_length, neural_network, hidden_size):
    hidden = zeros(size=hidden_size)  # initialize with zeros for each independent time series separately
    y_pred = zeros(size=sequence_length)
    for i in range(sequence_length):
        y_pred[i], hidden = neural_network(x[i], hidden)  # update hidden state
    return y_pred

Современные библиотеки предоставляют реализации вышеупомянутых функций, оптимизированные во время выполнения, или позволяют ускорить медленный цикл за счет своевременной компиляции .

Обучение

Учитель заставляет

Кодер-декодер RNN без механизма внимания. Принуждение учителя показано красным.

RNN можно обучить условно генеративной модели последовательностей, известной как авторегрессия .

Конкретно рассмотрим задачу машинного перевода, то есть задана последовательность $(x_{1},x_{2},\dots ,x_{n})$ английских слов, модель состоит в том, чтобы создать последовательность $(y_{1},\dots ,y_{m})$ французских слов. Эту проблему необходимо решить с помощью модели seq2seq .

Теперь во время обучения половина модели кодировщика сначала будет принимать $(x_{1},x_{2},\dots ,x_{n})$, то половина декодера начнет генерировать последовательность $({\hat {y}}_{1},{\hat {y}}_{2},\dots ,{\hat {y}}_{l})$. Проблема в том, что если модель допускает ошибку на раннем этапе, скажем, на ${\hat {y}}_{2}$, то последующие токены, скорее всего, также будут ошибками. Это делает получение модели обучающего сигнала неэффективным, поскольку модель в основном будет учиться сдвигать ${\hat {y}}_{2}$ к $y_{2}$, но не остальные.

Принуждение учителя позволяет декодеру использовать правильную выходную последовательность для генерации следующей записи в последовательности. Так, например, он увидит $(y_{1},\dots ,y_{k})$ для того, чтобы генерировать ${\hat {y}}_{k+1}$.

Градиентный спуск

Основные статьи: Градиентный спуск и проблема исчезающего градиента

Градиентный спуск — это первого порядка итеративный оптимизации алгоритм для поиска минимума функции. что нелинейные функции активации дифференцируемы В нейронных сетях его можно использовать для минимизации ошибки путем изменения каждого веса пропорционально производной ошибки по этому весу, при условии , . Различные методы для этого были разработаны в 1980-х и начале 1990-х годов Вербосом , Уильямсом , Робинсоном , Шмидхубером , Хохрайтером , Перлмуттером и другими.

Стандартный метод называется « обратным распространением ошибки во времени » или BPTT и представляет собой обобщение обратного распространения ошибки для сетей с прямой связью. Как и этот метод, он является примером автоматического дифференцирования в режиме обратного накопления принципа минимума Понтрягина . Более затратный в вычислительном отношении онлайн-вариант называется «Рекуррентное обучение в реальном времени» или RTRL. что является примером автоматического дифференцирования в режиме прямого накопления со сложенными касательными векторами. В отличие от BPTT, этот алгоритм является локальным во времени, но не локальным в пространстве.

В этом контексте локальность в пространстве означает, что весовой вектор единицы может быть обновлен с использованием только информации, хранящейся в подключенных единицах и самой единице, так что сложность обновления одной единицы является линейной по размерности весового вектора. Локальное по времени означает, что обновления происходят постоянно (онлайн) и зависят только от самого последнего временного шага, а не от нескольких временных шагов в пределах заданного временного горизонта, как в BPTT. Биологические нейронные сети кажутся локальными как во времени, так и в пространстве.

Для рекурсивного вычисления частных производных RTRL имеет временную сложность O (количество скрытых x весов) на временной шаг для вычисления матриц Якоби , в то время как BPTT принимает только O (количество весов) на временной шаг, за счет сохранения всех активных активаций в течение заданного временного интервала. Существует онлайн-гибрид между BPTT и RTRL промежуточной сложности. наряду с вариантами для непрерывного времени.

Основная проблема градиентного спуска для стандартных архитектур RNN заключается в том, что градиенты ошибок исчезают экспоненциально быстро с увеличением временного лага между важными событиями. LSTM в сочетании с гибридным методом обучения BPTT/RTRL пытается преодолеть эти проблемы. Эта задача также решается в независимо рекуррентной нейронной сети (IndRNN). путем сведения контекста нейрона к его собственному прошлому состоянию, и затем межнейронную информацию можно исследовать на следующих уровнях. Воспоминания разных диапазонов, включая долговременную память, можно изучить без проблемы исчезновения и взрыва градиента.

Онлайн-алгоритм, называемый причинно-рекурсивным обратным распространением ошибки (CRBP), реализует и объединяет парадигмы BPTT и RTRL для локально рекуррентных сетей. Он работает с наиболее распространенными локально-рекуррентными сетями. Алгоритм CRBP может минимизировать глобальную ошибку. Этот факт повышает стабильность алгоритма, обеспечивая единое представление о методах расчета градиента для рекуррентных сетей с локальной обратной связью.

Один из подходов к вычислению градиентной информации в RNN с произвольной архитектурой основан на построении диаграмм графов потока сигналов. Он использует пакетный алгоритм BPTT, основанный на теореме Ли для расчета чувствительности сети. Его предложили Ван и Бофейс, а его быструю онлайн-версию предложили Камполуччи, Унчини и Пьяцца.

Методы глобальной оптимизации

Обучение весов в нейронной сети можно смоделировать как задачу нелинейной глобальной оптимизации . Целевую функцию можно сформировать для оценки пригодности или ошибки конкретного вектора весов следующим образом: во-первых, веса в сети устанавливаются в соответствии с вектором весов. Затем сеть оценивается по обучающей последовательности. Обычно разница суммы квадратов между прогнозами и целевыми значениями, указанными в обучающей последовательности, используется для представления ошибки текущего весового вектора. Затем для минимизации этой целевой функции можно использовать произвольные методы глобальной оптимизации.

Наиболее распространенным методом глобальной оптимизации для обучения RNN являются генетические алгоритмы , особенно в неструктурированных сетях.

Первоначально генетический алгоритм кодируется с помощью весов нейронной сети заранее определенным образом, где один ген в хромосоме представляет одно весовое звено. Вся сеть представлена ​​в виде одной хромосомы. Функция приспособленности оценивается следующим образом:

• Каждый вес, закодированный в хромосоме, присваивается соответствующему весовому звену сети.
• Обучающий набор предоставляется сети, которая распространяет входные сигналы вперед.
• Среднеквадратическая ошибка возвращается в функцию фитнеса.
• Эта функция управляет процессом генетического отбора.

Многие хромосомы составляют популяцию; поэтому развивается множество различных нейронных сетей до тех пор, пока не будет выполнен критерий остановки. Распространенная схема остановки:

• Когда нейронная сеть изучила определенный процент обучающих данных или
• Когда минимальное значение среднеквадратической ошибки удовлетворяется или
• Когда достигнуто максимальное количество обучающих поколений.

Функция пригодности оценивает критерий остановки, поскольку она получает среднеквадратическую ошибку, обратную от каждой сети во время обучения. Следовательно, цель генетического алгоритма — максимизировать функцию приспособленности, уменьшив среднеквадратическую ошибку.

Для поиска хорошего набора весов можно использовать другие методы глобальной (и/или эволюционной) оптимизации, такие как моделирование отжига или оптимизация роя частиц .

Непрерывное время

Рекуррентная нейронная сеть непрерывного времени (CTRNN) использует систему обыкновенных дифференциальных уравнений для моделирования воздействия на нейрон входящих входных данных. Они обычно анализируются теорией динамических систем . Многие модели RNN в нейробиологии работают в непрерывном времени.

Для нейрона $i$ в сети с активацией $y_{i}$, скорость изменения активации определяется выражением:

$\tau _{i}{\dot {y}}_{i}=-y_{i}+\sum _{j=1}^{n}w_{ji}\sigma (y_{j}-\Theta _{j})+I_{i}(t)$

Где:

• $\tau _{i}$ : Постоянная времени постсинаптического узла
• $y_{i}$ : Активация постсинаптического узла.
• ${\dot {y}}_{i}$ : Скорость изменения активации постсинаптического узла.
• $w{}_{ji}$ : Вес соединения от пре- к постсинаптическому узлу.
• $\sigma (x)$ : Сигмовидная часть x, например $\sigma (x)=1/(1+e^{-x})$.
• $y_{j}$ : Активация пресинаптического узла.
• $\Theta _{j}$ : Смещение пресинаптического узла
• $I_{i}(t)$ : Ввод (если есть) в узел

CTRNN были применены в эволюционной робототехнике , где они использовались для решения проблем зрения, сотрудничество, и минимальное когнитивное поведение.

Обратите внимание, что согласно теореме выборки Шеннона рекуррентные нейронные сети с дискретным временем можно рассматривать как рекуррентные нейронные сети с непрерывным временем, в которых дифференциальные уравнения преобразуются в эквивалентные разностные уравнения . Эту трансформацию можно рассматривать как происходящую после активации постсинаптического узла. $y_{i}(t)$ были подвергнуты низкочастотной фильтрации, но до отбора проб.

На самом деле это рекурсивные нейронные сети с особой структурой: линейной цепочкой. В то время как рекурсивные нейронные сети работают с любой иерархической структурой, объединяя дочерние представления с родительскими представлениями, рекуррентные нейронные сети работают с линейной прогрессией времени, объединяя предыдущий временной шаг и скрытое представление в представление для текущего временного шага.

С точки зрения временных рядов, RNN могут выглядеть как нелинейные версии фильтров с конечной импульсной характеристикой и фильтрами с бесконечной импульсной характеристикой , а также как нелинейная авторегрессионная экзогенная модель (NARX). RNN имеет бесконечную импульсную характеристику, тогда как сверточные нейронные сети имеют конечную импульсную характеристику. Оба класса сетей демонстрируют временное динамическое поведение . Конечная импульсная рекуррентная сеть представляет собой направленный ациклический граф , который можно развернуть и заменить нейронной сетью строго прямого распространения, тогда как бесконечная импульсная рекуррентная сеть представляет собой ориентированный циклический граф , который не может быть развернут.

Эффект обучения на основе памяти для распознавания последовательностей также может быть реализован с помощью более биологической модели, которая использует механизм молчания, проявляющийся в нейронах с относительно высокочастотной пиковой активностью.

Дополнительные сохраненные состояния и хранилище под непосредственным управлением сети могут быть добавлены как в бесконечно-импульсные , так и в конечно-импульсные сети. Другая сеть или граф также может заменить хранилище, если оно включает временные задержки или петли обратной связи. Такие контролируемые состояния называются вентильными состояниями или вентилируемой памятью и являются частью сетей долгосрочной краткосрочной памяти (LSTM) и вентилируемых рекуррентных единиц . Это также называется нейронной сетью обратной связи (FNN).

Библиотеки

• Апач Синга
• Кафе : создано Центром видения и обучения Беркли (BVLC). Он поддерживает как процессор, так и графический процессор. Разработан на C++ и имеет Python и MATLAB . оболочки
• Chainer : полностью на Python, производственная поддержка процессоров, графических процессоров, распределенное обучение.
• Deeplearning4j : глубокое обучение Java и Scala с поддержкой нескольких графических процессоров в Spark .
• Flux : включает интерфейсы для RNN, включая GRU и LSTM, написанные на Julia .
• Keras : API высокого уровня, предоставляющий оболочку для многих других библиотек глубокого обучения.
• Когнитивный инструментарий Microsoft
• MXNet : платформа глубокого обучения с открытым исходным кодом, используемая для обучения и развертывания глубоких нейронных сетей.
• PyTorch : тензоры и динамические нейронные сети на Python с ускорением на графическом процессоре.
• TensorFlow Google : Theano-подобная библиотека под лицензией Apache 2.0 с поддержкой CPU, GPU и фирменного TPU . мобильный
• Theano : библиотека глубокого обучения для Python с API, в значительной степени совместимым с библиотекой NumPy .
• Torch : среда научных вычислений с поддержкой алгоритмов машинного обучения, написанная на C и Lua .

Приложения

Приложения рекуррентных нейронных сетей включают:

• Машинный перевод
• Управление роботом
• Прогнозирование временных рядов
• Распознавание речи
• Синтез речи
• Интерфейсы мозг-компьютер
• Обнаружение аномалий временных рядов
• Модель преобразования текста в видео
• Обучение ритму
• Музыкальная композиция
• Изучение грамматики
• Распознавание рукописного ввода
• Распознавание действий человека
• Обнаружение гомологии белков
• Прогнозирование субклеточной локализации белков
• Некоторые задачи прогнозирования в области управления бизнес-процессами
• Прогнозирование в путях оказания медицинской помощи
• Прогнозы разрушения термоядерной плазмы в реакторах (код Fusion Recurrent Neural Network (FRNN))

Дальнейшее чтение

• Мандич, Данило П.; Чемберс, Джонатон А. (2001). Рекуррентные нейронные сети для прогнозирования: алгоритмы обучения, архитектура и стабильность . Уайли. ISBN  978-0-471-49517-8 .
• Гроссберг, Стивен (22 февраля 2013 г.). «Рекуррентные нейронные сети» . Схоларпедия . 8 (2): 1888. Бибкод : 2013SchpJ...8.1888G . doi : 10.4249/scholarpedia.1888 . ISSN   1941-6016 .
• Рекуррентные нейронные сети с более чем 60 статьями RNN Юргена Шмидхубера группы в Институте исследований искусственного интеллекта Далле Молле.