Дельта-потенциал

В квантовой механике дельта -потенциал — это потенциальная яма, математически описываемая дельта-функцией Дирака — обобщенной функцией . Качественно он соответствует потенциалу, который везде равен нулю, кроме одной точки, где он принимает бесконечное значение. Это можно использовать для моделирования ситуаций, когда частица может свободно перемещаться в двух областях пространства с барьером между двумя областями. Например, электрон может почти свободно перемещаться в проводящем материале, но если две проводящие поверхности расположить близко друг к другу, граница между ними действует как барьер для электрона, который можно аппроксимировать дельта-потенциалом.

Дельта-потенциальная яма представляет собой предельный случай конечной потенциальной ямы , которая получается, если сохранить произведение ширины ямы и постоянного потенциала при уменьшении ширины ямы и увеличении потенциала.

В этой статье для простоты рассматривается только одномерная потенциальная яма, но анализ можно расширить и на большее количество измерений.

Одиночный дельта-потенциал

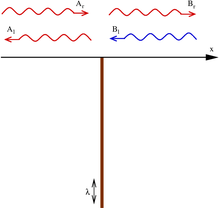
Независимое от времени уравнение Шредингера для волновой функции ψ ( x ) частицы в одном измерении в потенциале V ( x ) имеет вид $$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi (x)}{dx^{2}}}+V(x)\psi (x)=E\psi (x),$$где ħ — приведенная постоянная Планка , а E — энергия частицы.

Дельта-потенциал – это потенциал $$V(x)=\lambda \delta (x),$$где δ ( x ) — дельта-функция Дирака .

Он называется дельта-потенциальной ямой, если λ отрицателен, и дельта-потенциальным барьером, если λ положителен. Для простоты дельта была определена как начало координат; сдвиг аргумента дельта-функции не меняет ни одного из следующих результатов.

Решение уравнения Шрёдингера

Источник:

Потенциал делит пространство на две части ( x < 0 и x > 0 ). В каждой из этих частей потенциал равен нулю, и уравнение Шрёдингера сводится к $${\frac {d^{2}\psi }{dx^{2}}}=-{\frac {2mE}{\hbar ^{2}}}\psi ;$$ это линейное дифференциальное уравнение с постоянными коэффициентами , решениями которого являются линейные комбинации e ^ikx и е ^{− ikx} , где волновое число k связано с энергией соотношением $$k={\frac {\sqrt {2mE}}{\hbar }}.$$

В общем случае из-за наличия дельта-потенциала в начале координат коэффициенты решения не обязательно должны быть одинаковыми в обоих полупространствах: $$\psi (x)={\begin{cases}\psi _{\text{L}}(x)=A_{\text{r}}e^{ikx}+A_{\text{l}}e^{-ikx},&{\text{ if }}x<0,\\\psi _{\text{R}}(x)=B_{\text{r}}e^{ikx}+B_{\text{l}}e^{-ikx},&{\text{ if }}x>0,\end{cases}}$$где в случае положительных энергий (действительного k ) e ^ikx представляет собой волну, бегущую вправо, а e ^{− ikx} один движется влево.

Соотношение между коэффициентами можно получить, предполагая, что волновая функция непрерывна в начале координат: $$\psi (0)=\psi _{L}(0)=\psi _{R}(0)=A_{r}+A_{l}=B_{r}+B_{l},$$

Второе соотношение можно найти, изучая производную волновой функции. Обычно мы могли бы также наложить дифференцируемость в начале координат, но это невозможно из-за дельта-потенциала. Однако, если мы проинтегрируем уравнение Шредингера вокруг x = 0 в интервале [− ε , + ε ] : $$-{\frac {\hbar ^{2}}{2m}}\int _{-\varepsilon }^{+\varepsilon }\psi ''(x)\,dx+\int _{-\varepsilon }^{+\varepsilon }V(x)\psi (x)\,dx=E\int _{-\varepsilon }^{+\varepsilon }\psi (x)\,dx.$$

В пределе ε → 0 правая часть этого уравнения обращается в нуль; левая часть становится $$-{\frac {\hbar ^{2}}{2m}}[\psi _{R}'(0)-\psi _{L}'(0)]+\lambda \psi (0),$$ потому что $$\int _{-\varepsilon }^{+\varepsilon }\psi ''(x)\,dx=[\psi '(+\varepsilon )-\psi '(-\varepsilon )].$$ Подстановка определения ψ в это выражение дает $$-{\frac {\hbar ^{2}}{2m}}ik(-A_{r}+A_{l}+B_{r}-B_{l})+\lambda (A_{r}+A_{l})=0.$$

Таким образом, граничные условия дают следующие ограничения на коэффициенты $${\begin{cases}A_{r}+A_{l}-B_{r}-B_{l}&=0,\\-A_{r}+A_{l}+B_{r}-B_{l}&={\frac {2m\lambda }{ik\hbar ^{2}}}(A_{r}+A_{l}).\end{cases}}$$

Связанное состояние ( E <0)

График решения волновой функции связанного состояния для потенциала дельта-функции непрерывен всюду, но его производная не определена при x = 0 .

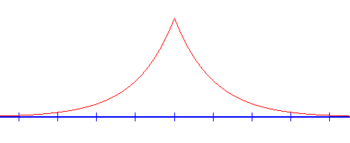
В любом одномерном притягивающем потенциале будет связанное состояние . Чтобы найти его энергию, заметим, что при E < 0 k = i √ 2 m | Е | / ħ = iκ является мнимым, и волновые функции, которые колебались для положительных энергий в приведенных выше расчетах, теперь являются экспоненциально возрастающими или убывающими функциями x (см. Выше). Требование, чтобы волновые функции не расходились на бесконечности, устраняет половину членов: A _r = B _l = 0 . Волновая функция тогда $$\psi (x)={\begin{cases}\psi _{\text{L}}(x)=A_{\text{l}}e^{\kappa x},&{\text{ if }}x\leq 0,\\\psi _{\text{R}}(x)=B_{\text{r}}e^{-\kappa x},&{\text{ if }}x\geq 0.\end{cases}}$$

Из граничных условий и условий нормировки следует, что $${\begin{cases}A_{\text{l}}=B_{\text{r}}={\sqrt {\kappa }},\\\kappa =-{\frac {m\lambda }{\hbar ^{2}}},\end{cases}}$$откуда следует, что λ должно быть отрицательным, т. е. связанное состояние существует только для ямы, а не для барьера. Преобразование Фурье этой волновой функции является функцией Лоренца .

Тогда энергия связанного состояния равна $$E=-{\frac {\hbar ^{2}\kappa ^{2}}{2m}}=-{\frac {m\lambda ^{2}}{2\hbar ^{2}}}.$$

Рассеяние ( Е > 0)

прохождения ( T ) и отражения ( R Вероятность ) дельта-потенциальной ямы. Энергия E > 0 измеряется в единицах ${\frac {m\lambda ^{2}}{2\hbar ^{2}}}$. Пунктир: классический результат. Сплошная линия: квантовая механика.

При положительных энергиях частица может свободно перемещаться в любом полупространстве: x < 0 или x > 0 . Он может быть рассеян на потенциале дельта-функции.

следующей ситуации: частица падает на барьер с левой стороны ( Ar _{Квантовый случай можно изучить в} ) . Оно может быть отражено A l ₎ или передано ( Br ₍ ) .Чтобы найти амплитуды отражения и пропускания при падении слева, мы поместили в приведенные выше уравнения A _r = 1 (входящая частица), A _l = r (отражение), B _l = 0 (нет прибывающей частицы справа) и B _r = t (трансмиссия) и найдите r и t, хотя у нас нет никаких уравнений в t . Результат $$t={\cfrac {1}{1-{\cfrac {m\lambda }{i\hbar ^{2}k}}}},\quad r={\cfrac {1}{{\cfrac {i\hbar ^{2}k}{m\lambda }}-1}}.$$

Благодаря зеркальной симметрии модели амплитуды падения справа такие же, как и слева. В результате существует ненулевая вероятность. $$R=|r|^{2}={\cfrac {1}{1+{\cfrac {\hbar ^{4}k^{2}}{m^{2}\lambda ^{2}}}}}={\cfrac {1}{1+{\cfrac {2\hbar ^{2}E}{m\lambda ^{2}}}}}$$чтобы частица отразилась. Это не зависит от знака λ , т. е. барьер имеет такую ​​же вероятность отразить частицу, как и яма. Это существенное отличие от классической механики, где вероятность отражения от барьера равна 1 (частица просто отскакивает назад) и 0 для ямы (частица проходит через яму невозмущенно).

Вероятность передачи равна $$T=|t|^{2}=1-R={\cfrac {1}{1+{\cfrac {m^{2}\lambda ^{2}}{\hbar ^{4}k^{2}}}}}={\cfrac {1}{1+{\cfrac {m\lambda ^{2}}{2\hbar ^{2}E}}}}.$$

Замечания и применение

Представленный выше расчет на первый взгляд может показаться нереальным и вряд ли полезным. Однако она оказалась подходящей моделью для множества реальных систем.

Один из таких примеров касается границ раздела между двумя проводящими материалами. В объеме материалов движение электронов квазисвободно и может быть описано кинетическим членом приведенного выше гамильтониана с эффективной массой m . Зачастую поверхности таких материалов покрыты оксидными слоями или не идеальны по другим причинам. Этот тонкий непроводящий слой затем можно смоделировать с помощью локального потенциала дельта-функции, как указано выше. Электроны могут затем туннелировать из одного материала в другой, вызывая ток.

Работа сканирующего туннельного микроскопа (СТМ) основана на этом туннельном эффекте. В этом случае барьер возникает из-за воздуха между кончиком СТМ и лежащим под ним объектом. Сила барьера связана с тем, что разделение тем сильнее, чем дальше они находятся друг от друга. Более общую модель этой ситуации см. в разделе « Конечный потенциальный барьер (КМ)» . Потенциальный барьер дельта-функции представляет собой предельный случай рассматриваемой здесь модели для очень высоких и узких барьеров.

Вышеупомянутая модель одномерна, а пространство вокруг нас трехмерно. Так что, по сути, надо решать уравнение Шрёдингера в трёх измерениях. С другой стороны, многие системы изменяются только по одному направлению координат и трансляционно инвариантны по остальным. Тогда уравнение Шредингера может быть сведено к рассматриваемому здесь случаю с помощью анзаца для волновой функции типа $\Psi (x,y,z)=\psi (x)\phi (y,z)\,\!$.

В качестве альтернативы можно обобщить дельта-функцию, чтобы она существовала на поверхности некоторой области D (см. Лапласиан индикатора ).

Модель дельта-функции на самом деле представляет собой одномерную версию атома водорода в соответствии с методом размерного масштабирования, разработанным группой Дадли Р. Хершбаха. Модель дельта-функции становится особенно полезной с двухъямной моделью дельта-функции Дирака, которая представляет собой одномерную версию иона молекулы водорода , как показано в следующем разделе.

Двойной дельта-потенциал

Симметричные и антисимметричные волновые функции для модели дельта-функции Дирака с двумя ямами и «межъядерным» расстоянием R = 2.

Дельта-функция Дирака с двойной ямой моделирует двухатомную молекулу водорода соответствующим уравнением Шредингера: $$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi (x)}{dx^{2}}}+V(x)\psi (x)=E\psi (x),$$где потенциал сейчас $$V(x)=-q\left[\delta \left(x+{\frac {R}{2}}\right)+\lambda \delta \left(x-{\frac {R}{2}}\right)\right],$$где $0<R<\infty$ - «межъядерное» расстояние с пиками дельта-функции Дирака (отрицательными), расположенными при x = ± R /2 (на диаграмме показано коричневым цветом). Принимая во внимание связь этой модели с ее трехмерным молекулярным аналогом, мы используем атомные единицы и устанавливаем $\hbar =m=1$. Здесь $0<\lambda <1$ является формально регулируемым параметром. Из случая одной скважины мы можем вывести « анзац » для решения, которое будет $$\psi (x)=Ae^{-d\left|x+{\frac {R}{2}}\right|}+Be^{-d\left|x-{\frac {R}{2}}\right|}.$$Сопоставление волновой функции с пиками дельта-функции Дирака дает определитель $${\begin{vmatrix}q-d&qe^{-dR}\\q\lambda e^{-dR}&q\lambda -d\end{vmatrix}}=0,\quad {\text{where }}E=-{\frac {d^{2}}{2}}.$$Таким образом, $d$ оказывается, что он определяется псевдоквадратным уравнением $$d_{\pm }(\lambda )={\frac {1}{2}}q(\lambda +1)\pm {\frac {1}{2}}\left\{q^{2}(1+\lambda )^{2}-4\lambda q^{2}\left[1-e^{-2d_{\pm }(\lambda )R}\right]\right\}^{1/2},$$который имеет два решения $d=d_{\pm }$. В случае равных зарядов (симметричный гомоядерный случай) λ = 1 , и псевдоквадратичное уравнение сводится к $$d_{\pm }=q\left[1\pm e^{-d_{\pm }R}\right].$$Случай «+» соответствует волновой функции, симметричной относительно средней точки (показана на диаграмме красным), где A = B , и называется gerade . Соответственно, случай «-» — это волновая функция, антисимметричная относительно средней точки, где A = — B , и называемая унгераде (показана зеленым на диаграмме). Они представляют собой аппроксимацию двух низших дискретных энергетических состояний трехмерного мира. ${\ce {H2^+}}$ и полезны при его анализе. Аналитические решения для собственных значений энергии для случая симметричных зарядов имеют вид $$d_{\pm }=q+W(\pm qRe^{-qR})/R,$$где W — стандартная Ламберта W -функция . Обратите внимание, что наименьшая энергия соответствует симметричному решению $d_{+}$. В случае неравных зарядов и, если уж на то пошло, трехмерной молекулярной проблемы, решения даются путем обобщения функции Ламберта W (см. Функция Ламберта W § Обобщения ).

Один из наиболее интересных случаев — когда qR ≤ 1, что приводит к $d_{-}=0$. Таким образом, имеется нетривиальное решение в связанном состоянии с E = 0 . Для этих конкретных параметров возникает множество интересных свойств, одним из которых является необычный эффект, заключающийся в том, что коэффициент передачи равен единице при нулевой энергии.

См. также

• Свободная частица
• Частица в коробке
• Конечная потенциальная яма
• Частица в кольце
• Частица в сферически-симметричном потенциале
• Квантовый гармонический осциллятор
• Атом водорода или водородоподобный атом
• Кольцевой волновод
• Частица в одномерной решетке (периодический потенциал)
• Молекулярный ион водорода
• Метод Гольштейна – Херринга
• Лапласиан индикатора
• Список квантовомеханических систем с аналитическими решениями

Ссылки

• Гриффитс, Дэвид Дж. (2005). Введение в квантовую механику (2-е изд.). Прентис Холл. стр. 68–78. ISBN  978-0-13-111892-8 .
• Для трехмерного случая ищите «потенциал дельта-оболочки»; далее см. К. Готфрид (1966), Квантовая механика, том I: Основы , гл. III, сек. 15.

Внешние ссылки

• СМИ, связанные с потенциалом Дельты, на Викискладе?