✖


Jump to content

Пятеричные 6-ортоплексы

    Add links
    (Перенаправлено с Pentiruncitусеченного 6-куба )
    Ортогональные проекции в B 6 плоскости Кокстера

    6-ортоплекс

    Пятеричный 6-ортоплекс
    Пятиугольный 6-куб

    6-куб.

    Пятиусеченный 6-ортоплекс

    Пятиконтеллярный 6-ортоплекс

    Пентикантиусеченный 6-ортоплекс

    Пятиусеченный 6-ортоплекс

    Пятирунчикантеллированный, 6-кубический

    Пентирунсикантиусеченный 6-ортоплекс

    Пентистеритусеченный 6-кубовый

    Пентистерикантиусеченный 6-ортоплекс

    Пентистерирунцикантиусеченный 6-ортоплекс
    ( Всеусеченный 6-куб )

    В шестимерной геометрии пентелтелированный 6-ортоплекс представляет собой выпуклый однородный 6-многогранник с усечениями 5-го порядка правильного 6-ортоплекса .

    Существуют уникальные 16 степеней пентелляций 6-ортоплекса с перестановками усечений, кантелляций, ранцинаций и стерикаций. Показаны десять из них, а остальные шесть легче построить в виде пятиугольного 6-куба . Простой пятерчатый 6-ортоплекс (тот же, что и пятерчатый 5-куб) также называется расширенным 6-ортоплексом , построенным с помощью операции расширения, примененной к обычному 6-ортоплексу . Высшая форма, пентистерирунцикантиусеченный 6-ортоплекс , называется омниусеченным 6-ортоплексом со всеми узлами, окруженными кольцами.

    Пятиусеченный 6-ортоплекс

    [ редактировать ]
    Пятиусеченный 6-ортоплекс
    Тип однородный 6-многогранник
    Символ Шлефли т 0,1,5 {3,3,3,3,4}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 8640
    Вершины 1920
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Теритусеченный гексаконтатетрапетон (аббревиатура: tacox) (Джонатан Бауэрс) [1]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Пятиконтеллярный 6-ортоплекс

    [ редактировать ]
    Пятиконтеллярный 6-ортоплекс
    Тип однородный 6-многогранник
    Символ Шлефли т 0,2,5 {3,3,3,3,4}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 21120
    Вершины 3840
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Териромбированный гексаконтитетрапетон (аббревиатура: тапокс) (Джонатан Бауэрс) [2]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Пентикантиусеченный 6-ортоплекс

    [ редактировать ]
    Пентикантиусеченный 6-ортоплекс
    Тип однородный 6-многогранник
    Символ Шлефли т 0,1,2,5 {3,3,3,3,4}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 30720
    Вершины 7680
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Теригреаторромбовидный гексаконтитетрапетон (аббревиатура: тогриг) (Джонатан Бауэрс) [3]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Пятиусеченный 6-ортоплекс

    [ редактировать ]
    Пятиусеченный 6-ортоплекс
    Тип однородный 6-многогранник
    Символ Шлефли т 0,1,3,5 {3,3,3,3,4}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 51840
    Вершины 11520
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Териприсматоусеченный гексаконтитетрапетон (аббревиатура: токракс) (Джонатан Бауэрс) [4]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График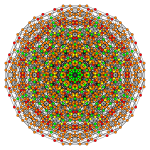
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Пентирунсикантиусеченный 6-ортоплекс

    [ редактировать ]
    Пентирунсикантиусеченный 6-ортоплекс
    Тип однородный 6-многогранник
    Символ Шлефли т 0,1,2,3,5 {3,3,3,3,4}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 80640
    Вершины 23040
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Теригреатопризматический гексаконтитетрапетон (аббревиатура: тагпог) (Джонатан Бауэрс) [5]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Пентистерикантиусеченный 6-ортоплекс

    [ редактировать ]
    Пентистерикантиусеченный 6-ортоплекс
    Тип однородный 6-многогранник
    Символ Шлефли т 0,1,2,4,5 {3,3,3,3,4}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 80640
    Вершины 23040
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Терицеллигреаторомбовидный гексаконтитетрапетон (аббревиатура: текагорг) (Джонатан Бауэрс) [6]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]


    [ редактировать ]

    Эти многогранники входят в набор из 63 однородных 6-многогранников, сгенерированных из B 6 плоскости Кокстера , включая правильный 6-куб или 6-ортоплекс .

    Многогранники B6

    β6
    t1β6
    t2β6
    t2γ6
    t1γ6
    γ6
    t0,1β6
    t0,2β6

    t1,2β6
    t0,3β6
    t1,3β6
    t2,3γ6
    t0,4β6
    t1,4γ6
    t1,3γ6
    t1,2γ6

    t0,5γ6
    t0,4γ6
    t0,3γ6
    t0,2γ6
    t0,1γ6
    t0,1,2β6
    t0,1,3β6
    t0,2,3β6

    t1,2,3β6
    t0,1,4β6
    t0,2,4β6
    t1,2,4β6
    t0,3,4β6
    t1,2,4γ6
    t1,2,3γ6
    t0,1,5β6

    t0,2,5β6
    t0,3,4γ6
    t0,2,5γ6
    t0,2,4γ6
    t0,2,3γ6
    t0,1,5γ6
    t0,1,4γ6
    t0,1,3γ6

    t0,1,2γ6
    t0,1,2,3β6
    t0,1,2,4β6
    t0,1,3,4β6
    t0,2,3,4β6
    t1,2,3,4γ6
    t0,1,2,5β6
    t0,1,3,5β6

    t0,2,3,5γ6
    t0,2,3,4γ6
    t0,1,4,5γ6
    t0,1,3,5γ6
    t0,1,3,4γ6
    t0,1,2,5γ6
    t0,1,2,4γ6
    t0,1,2,3γ6

    t0,1,2,3,4β6
    t0,1,2,3,5β6
    t0,1,2,4,5β6
    t0,1,2,4,5γ6
    t0,1,2,3,5γ6
    t0,1,2,3,4γ6
    t0,1,2,3,4,5γ6

    Примечания

    [ редактировать ]
    1. ^ Клитцинг, (x4o3o3o3x3x - такокс)
    2. ^ Клитцинг, (x4o3o3x3o3x - тапокс)
    3. ^ Клитцинг, (x4o3o3x3x3x - тогриг)
    4. ^ Клитцинг, (x4o3x3o3x3x - токракс)
    5. ^ Клитцинг, (x4x3o3x3x3x - tagpog)
    6. ^ Клитцинг, (x4x3o3x3x3x - текагорг)

    Ссылки

    [ редактировать ]
    • ХСМ Коксетер :
      • HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
      • Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1]
        • (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
        • (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
        • (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
    • Нормана Джонсона Равномерные многогранники , Рукопись (1991)
      • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
    • Клитцинг, Ричард. «6D однородные многогранники (полипеты)» . x4o3o3o3x3x - такокс, x4o3o3x3o3x - тапокс, x4o3o3x3x3x - тогриг, x4o3o3o3x3x - токракс, x4x3o3x3x3x - тагпог, x4x3o3x3x3x - текагорг
    [ редактировать ]
    Фундаментальные выпуклые правильные и однородные многогранники размерностей 2–10.
    Семья н ​ Б н И 2 (п) / Д н Е 6 / Е 7 / Е 8 / Ж 4 / Г 2 Ч н
    Правильный многоугольник Треугольник Квадрат п-гон Шестиугольник Пентагон
    Однородный многогранник Тетраэдр Октаэдр • Куб Демикуб Додекаэдр • Икосаэдр
    Равномерный полихорон Пентахорон 16 ячеек • Тессеракт Демитессеракт 24-ячеечный 120 ячеек • 600 ячеек
    Равномерный 5-многогранник 5-симплекс 5-ортоплекс • 5-куб 5-демикуб
    Равномерный 6-многогранник 6-симплекс 6-ортоплекс • 6-куб 6-демикуб 1 22 • 2 21
    Равномерный 7-многогранник 7-симплекс 7-ортоплекс • 7-куб 7-демикуб 1 32 • 2 31 • 3 21
    Равномерный 8-многогранник 8-симплекс 8-ортоплекс • 8-куб 8-демикуб 1 42 • 2 41 • 4 21
    Равномерный 9-многогранник 9-симплекс 9-ортоплекс • 9-куб 9-демикуб
    Равномерный 10-многогранник 10-симплекс 10-ортоплекс • 10-куб 10-демикуб
    Равномерный n - многогранник n - симплекс n - ортоплекс • n - куб n - демикуб 1 лиц 2 • 2 лиц 1 • лиц 21 n - пятиугольный многогранник
    Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений.
    Retrieved from "https://en.wikipedia.org/w/index.php?title=Pentellated_6-orthoplexes&oldid=787496899#Pentiruncitruncated_6-cube"
    Arc.Ask3.Ru: конец переведенного документа.
    Arc.Ask3.Ru
    Номер скриншота №: f8865bc64bb985be62aaf5458aacffd2__1498406580
    URL1:https://arc.ask3.ru/arc/aa/f8/d2/f8865bc64bb985be62aaf5458aacffd2.html
    Заголовок, (Title) документа по адресу, URL1:
    Pentellated 6-orthoplexes - Wikipedia
    Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)