✖


Jump to content

Пятиугольные 6-кубики

    Add links
    (Перенаправлено с Penticantitruncated 6-cube )

    6-куб.

    6-ортоплекс

    Пятиугольный 6-куб

    Пятиусеченный 6-куб

    Пятиконтеллярный 6-кубовый

    Пентикантиусеченный 6-кубовый

    Пятикруглоусеченный 6-кубический

    Пятирунчикантеллированный, 6-кубический

    Пятигранникусеченный 6-кубический

    Пентистеритусеченный 6-кубовый

    Пентистерикантиусеченный 6-куб.

    Всеусеченный 6-куб
    Ортогональные проекции в B 6 плоскости Кокстера

    В шестимерной геометрии пятимерный 6-куб представляет собой выпуклый однородный 6-мерный многогранник с усечениями 5-го порядка правильного 6-куба .

    Существуют уникальные 16 степеней пентелляций 6-куба с перестановками усечений, кантелляций, спиралей и стерикаций. Простой пятиугольный 6-куб также называется расширенным 6-кубом , он построен с помощью операции расширения, примененной к обычному 6-кубу . Высшая форма, пентистерирунсикантиусеченный 6-куб , называется всеусеченным 6-кубом со всеми узлами, окруженными кольцами. Шесть из них лучше построить из 6-ортоплекса, данного в пятеричном 6-ортоплексе .

    Пятиугольный 6-куб

    [ редактировать ]
    Пятиугольный 6-куб
    Тип Равномерный 6-многогранник
    Символ Шлефли т 0,5 {4.3.3.3.3}
    Диаграмма Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 1920
    Вершины 384
    Вершинная фигура 5-ячеечная антипризма
    Группа Коксетера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Пятеричный 6-ортоплекс
    • Расширенный 6-куб, расширенный 6-ортоплекс
    • Маленький тери-гексерактигексаконтитетрапетон (аббревиатура: стоксог) (Джонатан Бауэрс) [1]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Пятиусеченный 6-куб

    [ редактировать ]
    Пятиусеченный 6-куб
    Тип однородный 6-многогранник
    Символ Шлефли т 0,1,5 {4,3,3,3,3}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 8640
    Вершины 1920
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Теритусеченный гексеракт (аббревиатура: таког) (Джонатан Бауэрс) [2]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Пятиконтеллярный 6-кубовый

    [ редактировать ]
    Пятиконтеллярный 6-кубовый
    Тип однородный 6-многогранник
    Символ Шлефли т 0,2,5 {4,3,3,3,3}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 21120
    Вершины 3840
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Терирромбированный гексеракт (аббревиатура: топаг) (Джонатан Бауэрс) [3]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Пентикантиусеченный 6-кубовый

    [ редактировать ]
    Пентикантиусеченный 6-кубовый
    Тип однородный 6-многогранник
    Символ Шлефли т 0,1,2,5 {4,3,3,3,3}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 30720
    Вершины 7680
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Теригреаторромбовидный гексеракт (аббревиатура: тогрикс) (Джонатан Бауэрс) [4]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Пятикруглоусеченный 6-кубический

    [ редактировать ]
    Пятикруглоусеченный 6-кубический
    Тип однородный 6-многогранник
    Символ Шлефли т 0,1,3,5 {4,3,3,3,3}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 151840
    Вершины 11520
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Терицеллиромбовидный гексаконтитетрапетон (аббревиатура: токраг) (Джонатан Бауэрс) [5]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График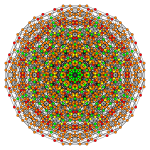
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Пятирунчикантеллированный, 6-кубический

    [ редактировать ]
    Пятирунчикантеллированный, 6-кубический
    Тип однородный 6-многогранник
    Символ Шлефли т 0,2,3,5 {4,3,3,3,3}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 46080
    Вершины 11520
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Терипризматоромби-гексерактигексаконтитетрапетон (аббревиатура: типриксог) (Джонатан Бауэрс) [6]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График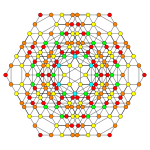
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Пятигранникусеченный 6-кубический

    [ редактировать ]
    Пятигранникусеченный 6-кубический
    Тип однородный 6-многогранник
    Символ Шлефли т 0,1,2,3,5 {4,3,3,3,3}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 80640
    Вершины 23040
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Теригреатопризматический гексеракт (аббревиатура: оспа) (Джонатан Бауэрс) [7]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Пентистеритусеченный 6-кубовый

    [ редактировать ]
    Пентистеритусеченный 6-кубовый
    Тип однородный 6-многогранник
    Символ Шлефли т 0,1,4,5 {4,3,3,3,3}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 30720
    Вершины 7680
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Терицеллитрунки-гексерактигексаконтитетрапетон (аббревиатура: тактаксог) (Джонатан Бауэрс) [8]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Пентистерикантиусеченный 6-куб.

    [ редактировать ]
    Пентистерикантиусеченный 6-куб.
    Тип однородный 6-многогранник
    Символ Шлефли т 0,1,2,4,5 {4,3,3,3,3}
    Диаграммы Кокстера-Динкина
    5-гранный
    4-ликий
    Клетки
    Лица
    Края 80640
    Вершины 23040
    Вершинная фигура
    Группы Кокстера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый

    Альтернативные названия

    [ редактировать ]
    • Терицеллигреатор ромбовидный гексеракт (аббревиатура: токагракс) (Джонатан Бауэрс) [9]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Всеусеченный 6-куб

    [ редактировать ]
    Всеусеченный 6-куб
    Тип Равномерный 6-многогранник
    Символ Шлефли т 0,1,2,3,4,5 {3 5 }
    Диаграммы Кокстера-Динкина
    5-гранный 728:
    12 т 0,1,2,3,4 {3,3,3,4}
    60 {}×t 0,1,2,3 {3,3,4} ×
    160 {6}×t 0,1,2 {3,4} ×
    240 {8}×t 0,1,2 {3,3} ×
    192 {}×t 0,1,2,3 {3 3 } ×
    64 т 0,1,2,3,4 {3 4 }
    4-ликий 14168
    Клетки 72960
    Лица 151680
    Края 138240
    Вершины 46080
    Вершинная фигура неправильный 5-симплекс
    Группа Коксетера Б 6 , [4,3,3,3,3]
    Характеристики выпуклый , изогональный

    Всеусеченный 6-куб имеет 5040 вершин , 15120 ребер , 16800 граней (4200 шестиугольников и 1260 квадратов ), 8400 ячеек , 1806 4-граней и 126 5-граней. Имея 5040 вершин, это самый большой из 35 однородных 6-многогранников, созданных из обычного 6-куба .

    Альтернативные названия

    [ редактировать ]
    • Пентистерирунсикантиусеченный 6-куб или 6-ортоплекс ( омниусечение для 6-многогранников)
    • Всеусеченный гексеракт
    • Большой тери-гексерактигексаконтитетрапетон (аббревиатура: gotaxog) (Джонатан Бауэрс) [10]

    Изображения

    [ редактировать ]
    орфографические проекции
    Самолет Коксетера Б 6 Б 5 Б 4
    График
    Двугранная симметрия [12] [10] [8]
    Самолет Коксетера BБ3 BБ2
    График
    Двугранная симметрия [6] [4]
    Самолет Коксетера AА5 AА3
    График
    Двугранная симметрия [6] [4]

    Полный курносый 6-кубовый

    [ редактировать ]

    Полный курносый 6-куб или омнискурносый 6-куб , определяемый как чередование всеусеченного 6-куба, не является однородным, но его можно представить диаграммой Коксетера. и симметрия [4,3,3,3,3] + , и построен из 12 курносых 5-кубов , 64 курносых 5-симплексов , 60 курносых тессерактных антипризм, 192 курносых 5-клеточных антипризм, 160 3-sr{4,3} дуоантипризм, 240 4-s{3,4} дуоантипризм, и 23040 неправильных 5-симплексов, заполняющих пробелы в удаленных вершинах.

    [ редактировать ]

    Эти многогранники входят в набор из 63 однородных 6-многогранников, сгенерированных из B 6 плоскости Кокстера , включая правильный 6-куб или 6-ортоплекс .

    Многогранники B6

    β6
    t1β6
    t2β6
    t2γ6
    t1γ6
    γ6
    t0,1β6
    t0,2β6

    t1,2β6
    t0,3β6
    t1,3β6
    t2,3γ6
    t0,4β6
    t1,4γ6
    t1,3γ6
    t1,2γ6

    t0,5γ6
    t0,4γ6
    t0,3γ6
    t0,2γ6
    t0,1γ6
    t0,1,2β6
    t0,1,3β6
    t0,2,3β6

    t1,2,3β6
    t0,1,4β6
    t0,2,4β6
    t1,2,4β6
    t0,3,4β6
    t1,2,4γ6
    t1,2,3γ6
    t0,1,5β6

    t0,2,5β6
    t0,3,4γ6
    t0,2,5γ6
    t0,2,4γ6
    t0,2,3γ6
    t0,1,5γ6
    t0,1,4γ6
    t0,1,3γ6

    t0,1,2γ6
    t0,1,2,3β6
    t0,1,2,4β6
    t0,1,3,4β6
    t0,2,3,4β6
    t1,2,3,4γ6
    t0,1,2,5β6
    t0,1,3,5β6

    t0,2,3,5γ6
    t0,2,3,4γ6
    t0,1,4,5γ6
    t0,1,3,5γ6
    t0,1,3,4γ6
    t0,1,2,5γ6
    t0,1,2,4γ6
    t0,1,2,3γ6

    t0,1,2,3,4β6
    t0,1,2,3,5β6
    t0,1,2,4,5β6
    t0,1,2,4,5γ6
    t0,1,2,3,5γ6
    t0,1,2,3,4γ6
    t0,1,2,3,4,5γ6

    Примечания

    [ редактировать ]
    1. ^ Клитцинг, (x4o3o3o3o3x - стоксог)
    2. ^ Клитцинг, (x4x3o3o3o3x - таког)
    3. ^ Клитцинг, (x4o3x3o3o3x - топаг)
    4. ^ Клитцинг, (x4x3x3o3o3x - тогрикс)
    5. ^ Клитцинг, (x4x3o3x3o3x - токраг)
    6. ^ Клитцинг, (x4o3x3x3o3x - типриксог)
    7. ^ Клитцинг, (x4x3x3o3x3x - оспа)
    8. ^ Клитцинг, (x4x3o3o3x3x - тактаксог)
    9. ^ Клитцинг, (x4x3x3o3x3x - токагракс)
    10. ^ Клитцинг, (x4x3x3x3x3x - gotaxog)

    Ссылки

    [ редактировать ]
    • ХСМ Коксетер :
      • HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
      • Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1]
        • (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
        • (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
        • (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
    • Нормана Джонсона Равномерные многогранники , Рукопись (1991)
      • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
    • Клитцинг, Ричард. «6D однородные многогранники (полипеты)» . x4o3o3o3o3x - стоксог, x4x3o3o3o3x - таког, x4o3x3o3o3x - топаг, x4x3x3o3o3x - тогрикс, x4x3o3x3o3x - токраг, x4o3x3x3o3x - типриксог, x4x3x3o3x3x - оспа, x4x3o3o3x3x - тактаксог, x4x3x3o3x3x - токагракс, x4x3x3x3x3x - gotaxog
    [ редактировать ]
    Фундаментальные выпуклые правильные и однородные многогранники размерностей 2–10.
    Семья н ​ Б н И 2 (п) / Д н Е 6 / Е 7 / Е 8 / Ж 4 / Г 2 Ч н
    Правильный многоугольник Треугольник Квадрат п-гон Шестиугольник Пентагон
    Однородный многогранник Тетраэдр Октаэдр • Куб Демикуб Додекаэдр • Икосаэдр
    Равномерный полихорон Пентахорон 16 ячеек • Тессеракт Демитессеракт 24-ячеечный 120 ячеек • 600 ячеек
    Равномерный 5-многогранник 5-симплекс 5-ортоплекс • 5-куб 5-демикуб
    Равномерный 6-многогранник 6-симплекс 6-ортоплекс • 6-куб 6-демикуб 1 22 • 2 21
    Равномерный 7-многогранник 7-симплекс 7-ортоплекс • 7-куб 7-демикуб 1 32 • 2 31 • 3 21
    Равномерный 8-многогранник 8-симплекс 8-ортоплекс • 8-куб 8-демикуб 1 42 • 2 41 • 4 21
    Равномерный 9-многогранник 9-симплекс 9-ортоплекс • 9-куб 9-демикуб
    Равномерный 10-многогранник 10-симплекс 10-ортоплекс • 10-куб 10-демикуб
    Равномерный n - многогранник n - симплекс n - ортоплекс • n - куб n - демикуб 1 лиц 2 • 2 лиц 1 • лиц 21 n - пятиугольный многогранник
    Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений.
    Retrieved from "https://en.wikipedia.org/w/index.php?title=Pentellated_6-cubes&oldid=1222139178#Penticantitruncated_6-cube"
    Arc.Ask3.Ru: конец переведенного документа.
    Arc.Ask3.Ru
    Номер скриншота №: 1ea98bd43ae110f76b08a512da22d6ab__1714783680
    URL1:https://arc.ask3.ru/arc/aa/1e/ab/1ea98bd43ae110f76b08a512da22d6ab.html
    Заголовок, (Title) документа по адресу, URL1:
    Pentellated 6-cubes - Wikipedia
    Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)