Выпрямленные 6-ортоплексы
 6-ортоплекс |  Выпрямленный 6-ортоплекс | 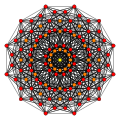 Биректифицированный 6-ортоплекс | |
 Биректифицированный 6-куб |  Ректифицированный 6-куб |  6-куб. | |
| Ортогональные проекции в B 6 плоскости Кокстера | |||
|---|---|---|---|
В шестимерной геометрии выпрямленный 6-ортоплекс — это выпуклый однородный 6-многогранник , являющийся выпрямлением правильного 6-ортоплекса .
Существует шесть уникальных степеней ректификации, нулевая из которых — 6-ортоплекс , а 6-я и последняя — 6-куб . Вершины выпрямленного 6-ортоплекса расположены в центрах ребер 6-ортоплекса. Вершины биректифицированного 6-ортоплекса расположены в центрах треугольных граней 6-ортоплекса.
Выпрямленный 6-ортоплекс
[ редактировать ]| Выпрямленный шестигранник | |
|---|---|
| Тип | однородный 6-многогранник |
| Символы Шлефли | т 1 {3 4 ,4} или r{3 4 ,4} г {3,3,3,3 1,1 } |
| Диаграммы Кокстера-Динкина | |
| 5-гранный | всего 76: 64 выпрямленный 5-симплекс 12 5-ортоплекс |
| 4-ликий | 576 всего: 192 выпрямленный 5-элементный 384 5-ячеечный |
| Клетки | 1200 всего: 240 октаэдр 960 тетраэдр |
| Лица | 1120 всего: Треугольники 160 и 960 градусов |
| Края | 480 |
| Вершины | 60 |
| Вершинная фигура | 16-ячеечная призма |
| Полигон Петри | Додекагон |
| Группы Кокстера | Б 6 , [3,3,3,3,4] Д 6 , [3 3,1,1 ] |
| Характеристики | выпуклый |
Выпрямленный 6-ортоплекс представляет собой вершинную фигуру полугексерактических сот .








 или
или 










Альтернативные названия
[ редактировать ]- выпрямленный шестигранник
- ректифицированный гексаконтитетрапетон (аббревиатура: тряпка) (Джонатан Бауэрс)
Строительство
[ редактировать ]Есть две группы Кокстера , связанные с выпрямленным гексакросом , одна с группой Кокстера C 6 или [4,3,3,3,3] и более низкая симметрия с двумя копиями граней пентакросса, чередующимися с D 6 или [ 3 3,1,1 ] Группа Кокстера.
Декартовы координаты
[ редактировать ]Декартовы координаты вершин выпрямленного шестиугольника с центром в начале координат, длина ребра все перестановки:
- (±1,±1,0,0,0,0)
Изображения
[ редактировать ]| Самолет Коксетера | Б 6 | Б 5 | Б 4 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [12] | [10] | [8] |
| Самолет Коксетера | BБ3 | BБ2 | |
| График |  |  | |
| Двугранная симметрия | [6] | [4] | |
| Самолет Коксетера | AА5 | AА3 | |
| График | 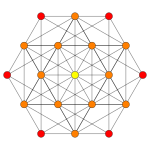 |  | |
| Двугранная симметрия | [6] | [4] |
Корневые векторы
[ редактировать ]60 вершин представляют корневые векторы простой группы Ли D 6 . Вершины можно увидеть в трех гиперплоскостях : 15 вершин представляют собой выпрямленные 5-симплексные ячейки на противоположных сторонах, а 30 вершин расширенного 5-симплекса проходят через центр. В сочетании с 12 вершинами 6-ортоплекса эти вершины представляют 72 корневых вектора B 6 и C 6 простых групп Ли .
60 корней D6 можно геометрически сложить в H3 ( симметрия икосаэдра ), как ![]()
![]()
![]()
![]()
![]() к
к ![]()
![]()
![]()
![]()
![]() с 30 вершинами , создавая 2 копии икосододекаэдров , с золотым сечением между их радиусами: [1]
с 30 вершинами , создавая 2 копии икосододекаэдров , с золотым сечением между их радиусами: [1]
| Выпрямленный 6-ортоплекс | 2 икосододекаэдра | |
|---|---|---|
| 3D (проекция H3) | A 4 /B 5 /D 6 Coxeter plane | H 2 Самолет Коксетера |
 |  |  |
Биректифицированный 6-ортоплекс
[ редактировать ]| Биректифицированный 6-ортоплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символы Шлефли | т 2 {3 4 ,4} или 2r{3 4 ,4} т 2 {3,3,3,3 1,1 } |
| Диаграммы Кокстера-Динкина | |
| 5-гранный | 76 |
| 4-ликий | 636 |
| Клетки | 2160 |
| Лица | 2880 |
| Края | 1440 |
| Вершины | 160 |
| Вершинная фигура | {3} × {3,4} дуопризма |
| Полигон Петри | Додекагон |
| Группы Кокстера | Б 6 , [3,3,3,3,4] Д 6 , [3 3,1,1 ] |
| Характеристики | выпуклый |
Биректифицированный 6-ортоплекс может замощить пространство в триректифицированных 6-кубических сотах .
Альтернативные названия
[ редактировать ]- двунаправленный шестигранник
- биректифицированный гексаконтитетрапетон (аббревиатура: хвастовство) (Джонатан Бауэрс)
Декартовы координаты
[ редактировать ]Декартовы координаты вершин выпрямленного шестиугольника с центром в начале координат, длина ребра все перестановки:
- (±1,±1,±1,0,0,0)
Изображения
[ редактировать ]| Самолет Коксетера | Б 6 | Б 5 | Б 4 |
|---|---|---|---|
| График | 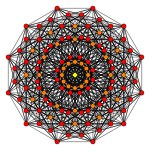 | 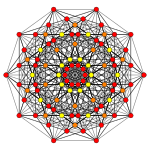 |  |
| Двугранная симметрия | [12] | [10] | [8] |
| Самолет Коксетера | BБ3 | BБ2 | |
| График | 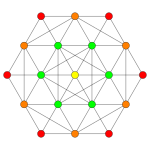 | 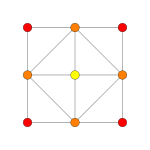 | |
| Двугранная симметрия | [6] | [4] | |
| Самолет Коксетера | AА5 | AА3 | |
| График | 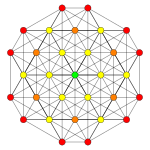 |  | |
| Двугранная симметрия | [6] | [4] |
Его также можно спроецировать в 3D-размеры, как ![]()
![]()
![]()
![]()
![]() →
→ ![]()
![]()
![]()
![]()
![]() , оболочка додекаэдра .
, оболочка додекаэдра .
Связанные многогранники
[ редактировать ]Эти многогранники являются частью семейства из 63 однородных 6-многогранников, созданных из B 6 плоскости Кокстера , включая правильный 6-куб или 6-ортоплекс .
| Многогранники B6 |
|---|
Примечания
[ редактировать ]- ↑ Икосододекаэдр из D6 Джона Баэза, 1 января 2015 г.
Ссылки
[ редактировать ]- ХСМ Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
- Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
- Клитцинг, Ричард. «6D однородные многогранники (полипеты)» . о3х3о3о3о4о - тряпка, о3о3х3о3о4о - хвастаться

































































