Список однородных многогранников по фигурам вершин
| Многогранник | |
| Сорт | Количество и свойства |
|---|---|
| Платоновые тела | ( 5 , выпуклый, правильный) |
| Архимедовы тела | ( 13 , выпуклый, однородный) |
| Многогранники Кеплера – Пуансо | ( 4 , правильный, невыпуклый) |
| Однородные многогранники | ( 75 , униформа) |
| Призматоид : призмы , антипризмы и т. д. | ( 4 бесконечных однородных класса) |
| Замощения многогранников | ( 11 обычных , в самолете) |
| Квазиправильные многогранники | ( 8 ) |
| Твердые вещества Джонсона | ( 92 , выпуклая, неоднородная) |
| Бипирамиды | ( бесконечный ) |
| Пирамиды | ( бесконечный ) |
| Звездочки | Звездочки |
| Полиэдрические соединения | ( 5 обычных ) |
| Дельтаэдры | ( Дельтаэдры , грани равностороннего треугольника) |
| Курносые многогранники | ( 12 униформ , не зеркальное отображение) |
| Зоноэдр | ( Зоноэдры , грани имеют симметрию 180°) |
| Двойной многогранник | |
| Самодвойственный многогранник | ( бесконечный ) |
| Каталонский солид | ( 13 , архимедово двойственное) |
существует множество отношений Между однородными многогранниками . [1] [2] [3] Некоторые получаются путем усечения вершин правильного или квазиправильного многогранника.Другие имеют те же вершины и ребра, что и другие многогранники.Группировка ниже демонстрирует некоторые из этих отношений.
Вершинная фигура многогранника
[ редактировать ]Отношения можно сделать очевидными, исследуя фигуры вершин, полученные путем перечисления граней, прилегающих к каждой вершине (помните, что для однородных многогранников все вершины одинаковы, то есть вершинно-транзитивны ). Например, куб имеетвершина рисунка 4.4.4, то есть три смежные квадратные грани.Возможные лица:
- 3 – равносторонний треугольник
- 4 - квадрат
- 5 – правильный пятиугольник
- 6 – правильный шестигранник
- 8 – правильный восьмиугольник
- 10 – правильный десятиугольник
- 5/2 – пентаграмма
- 8/3 – октаграмма
- 10/3 - декаграмм
Некоторые лица появятся с обратной ориентацией, которая записана здесь как
- -3 — треугольник с обратной ориентацией (часто пишется как 3/2)
Другие проходят через начало координат, которое мы пишем как
- 6* - шестиугольник, проходящий через начало координат
Символ Витгофа связывает многогранник со сферическими треугольниками . Символы Витхоффа пишутсяр|qr, pq|r, pqr| где сферический треугольник имеет углы π/p, π/q, π/r, черта указывает положение вершин относительно треугольника.

Джонсон (2000) классифицировал однородные многогранники следующим образом:
- Регулярные (правильные многоугольные вершинные фигуры): p д , символ Витгофа q|p 2
- Квазирегулярные (прямоугольные или двуугольные вершинные фигуры): pqpq 2|pq или pqpqpq, символ Витхоффа 3|pq
- Верси-регулярные (ортодиагональные вершинные фигуры), pq*.-pq*, символ Витхоффа qq|p
- Усеченные правильные (равнобедренные треугольные вершинные фигуры): ppq, символ Витхоффа q 2|p
- Верзи-квазирегулярные (диптероидные вершинные фигуры), pqpr Символ Витхоффа qr|p
- Квазиквазирегулярные (вершинные фигуры трапеции): p*.qp*.-r qr|p или pq*.-pq* pqr|
- Усеченные квазиправильные (разносторонние треугольные вершинные фигуры), pqr Символ Витхоффа pqr|
- Курносые квазиправильные (пятиугольные, шестиугольные или восьмиугольные вершинные фигуры), символ Витхоффа pqr|
- Призмы (усеченные осоэдры),
- Антипризмы и скрещенные антипризмы (взносые диэдры)
Формат каждого рисунка соответствует одному и тому же основному шаблону.
- изображение многогранника
- название многогранника
- альтернативные названия (в скобках)
- Символ Витхоффа
- Системы нумерации: W — число, используемое Веннингером в моделях многогранников , U — равномерная индексация, K — индексация Калейдо, C — нумерация, используемая в Коксетере и др. «Равномерные многогранники».
- Количество вершин V, ребер E, Граней F и количество граней по типу.
- Эйлерова характеристика χ = V - E + F
Фигуры вершин расположены слева, за ними следуют группы точек в трех измерениях. Семь оставшихся групп точек : тетраэдрические T d , октаэдрические Oh или икосаэдрические I h .
Усеченные формы
[ редактировать ]Правильные многогранники и их усеченные формы.
[ редактировать ]В столбце А перечислены все правильные многогранники.в столбце B перечислены их усеченные формы.Все правильные многогранники имеют вершинные фигуры p р : ppp и т. д. и символ Витхоффа р|q р. Усеченные формы имеют вершинную фигуру qqr (где q=2p и r) и Витхоффа pq|r.
| вершина фигуры | группа | А: обычный: ппп | B: усеченное обычное: ppr |
| Т д |
|
| |
 3.3.3.3 | Ой |
|
|
 4.4.4 | Ой |
|
|
| I h |
|
| |
 5.5.5 | I h |
|
|
| I h |
|
| |
 3.3.3.3.3 | I h |
|
|
| I h |
| ||
| I h |
|
Кроме того, существуют три квазиусеченные формы. Они также классифицируются как усеченно-правильные многогранники.
| вершинные фигуры | Группа О ч | Группа I ч | Группа I ч |
|
|
|
Усеченные формы квазиправильных многогранников
[ редактировать ]В столбце A перечислены некоторые квазиправильные многогранники.в столбце B перечислены обычные усеченные формы,в столбце C показаны квазиусеченные формы,в столбце D показан другой метод усечения.Все эти усеченные формы имеют вершинную фигуру pqr иВитхоффсимвол pqr|.
| вершина фигуры | группа | A: квазирегулярный: pqpq | B: усеченный квазирегулярный: pqr | C: усеченный квазирегулярный: pqr | D: усеченный квазирегулярный: pqr |
 3.4.3.4 | Ой |
|
|
|
|
 3.5.3.5 | I h |
|
|
|
|
I h |
|
| |||
 3.5/2.3.5/2 | I h |
|
Многогранники, имеющие общие ребра и вершины
[ редактировать ]Обычный
[ редактировать ]Все они упоминаются в других местах, но эта таблица показывает некоторые взаимосвязи.Все они правильные, за исключением тетрагемигексаэдра, который является верзи-правильным.
| вершина фигуры | V | И | группа | обычный | обычная/обычная версия |
 3.3.3.3 3.4*.-3.4* | 6 | 12 | Ой |
|
|
| 12 | 30 | I h |
|
| |
| 12 | 30 | I h |
|
|
Квазирегулярные и регулярные по версиям
[ редактировать ]Прямоугольные вершинные фигуры или скрещенные прямоугольники.первый столбец — квазиправильные, второй и третий столбцы — полуэдры сграни, проходящие через начало координат, называют верзи-регулярными некоторые авторы .
| вершина фигуры | V | И | группа | квазирегулярный: pqpq | обычная версия: ps*.-ps* | верзи-регулярный: qs*.-qs* |
 3.4.3.4 | 12 | 24 | Ой |
|
|
|
 3.5.3.5 | 30 | 60 | I h |
|
|
|
 3.5/2.3.5/2 | 30 | 60 | Ih |
|
|
|
 5.5/2.5.5/2 | 30 | 60 | Ih |
|
|
|
Дитригональная обычная и обычная версия
[ редактировать ]Дитригональные (то есть ди(2)-три(3)-огональные) вершинные фигуры являются 3-кратным аналогом прямоугольника. Все они квазирегулярны, поскольку все ребра изоморфны.Соединение пятикубов имеет один и тот же набор ребер и вершин.Крестовые формы имеют неориентируемую фигуру вершины, поэтому обозначение «-» не использовалось, а грани «*» проходят рядом, а не через начало координат.
| вершина фигуры | V | И | группа | двуугольный | перекрестно-дитригональный | перекрестно-дитригональный |
 5/2.3.5/2.3.5/2.3 | 20 | 60 | Ih |
|
|
|
квазирегулярные и квазиквазирегулярные версии
[ редактировать ]Группа III: вершинные фигуры трапеции или скрещенной трапеции.В первый столбец входят выпуклые ромбические многогранники, созданные вставкой двух квадратов.в вершинные фигуры кубооктаэдра и икосододекаэдра.
| вершина фигуры | V | И | группа | трапеция: pqrq | перекрещенная трапеция: ps*.-rs* | перекрещенная трапеция: qs*.-qs* |
 3.4.4.4 | 24 | 48 | Ой |
|
|
|
 3.8/3.4.8/3 | 24 | 48 | Ой |
|
|
|
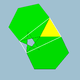
 3.4.5.4 | 60 | 120 | I h |
|
|
|
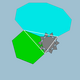
 5/2.4.5.4 | 60 | 120 | Ih |
|
|
|
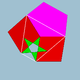
 3.10/3.5/2.10/3 | 60 | 120 | Ih |
|
|
|
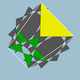
 3.6.5/2.6 | 60 | 120 | Ih |
|
|
|
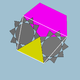 3.10/3.5.10/3 | 60 | 120 | Ih |
|
|
|
Ссылки
[ редактировать ]- ^ Коксетер, HSM ; Лонге-Хиггинс, MS ; Миллер, JCP (1954), «Равномерные многогранники», Philosophical Transactions of the the Royal Society of London , 246 : 401–450 (6 пластин), doi : 10.1098/rsta.1954.0003 , MR 0062446 .
- ^ Сопов С. П. (1970), "Доказательство полноты списка элементарных однородных многогранников", Украинский геометрический сборник (8): 139–156, MR 0326550 .
- ^ Скиллинг, Дж. (1975), «Полный набор однородных многогранников», Philosophical Transactions of the Royal Society of London , 278 : 111–135, doi : 10.1098/rsta.1975.0022 , MR 0365333 .