Предел (теория категорий)

В теории категорий , разделе математики , абстрактное понятие предела отражает существенные свойства универсальных конструкций, таких как произведения , обратные ограничения и обратные пределы . Двойственное понятие копредела обобщает такие конструкции, как непересекающиеся объединения , прямые суммы , копроизведения , выталкивания и прямые пределы .

Пределы и копределы, как и сильно связанные понятия универсальных свойств и сопряженных функторов , существуют на высоком уровне абстракции. Чтобы понять их, полезно сначала изучить конкретные примеры, которые эти концепции призваны обобщить.

Определение

Пределы и копределы в категории $C$ определяются с помощью диаграмм в $C$. Формально диаграмма формы $J$ в $C$ является функтором из $J$ к $C$:

$F:J\to C.$

Категория $J$ рассматривается как индексная категория , а диаграмма $F$ рассматривается как индексация набора объектов и морфизмов в $C$ по образцу $J$.

Чаще всего интересен случай, когда категория $J$— малая или даже конечная категория. Диаграмма называется маленькой или конечной , если $J$ является.

Ограничения

См. также: Обратный предел

Позволять $F:J\to C$ быть диаграммой формы $J$ в категории $C$. Конус для ​ $F$ это объект $N$ из $C$ вместе с семьей $\psi _{X}:N\to F(X)$ морфизмов, индексированных объектами $X$ из $J$, такой, что для любого морфизма $f:X\to Y$ в $J$, у нас есть $F(f)\circ \psi _{X}=\psi _{Y}$.

Предел ​ диаграммы $F:J\to C$ это конус $(L,\phi )$ к $F$ такой, что для каждого конуса $(N,\psi )$ к $F$ существует единственный морфизм $u:N\to L$ такой, что $\phi _{X}\circ u=\psi _{X}$ для всех $X$ в $J$.

A universal cone

Говорят, что конус $(N,\psi )$ факторы через конус $(L,\phi )$с уникальная факторизация $u$. Морфизм $u$ иногда называют опосредующим морфизмом .

Пределы также называют универсальными конусами , поскольку они характеризуются универсальным свойством (подробнее см. ниже). Как и любое универсальное свойство, приведенное выше определение описывает сбалансированное состояние общности: предельный объект $L$должен быть достаточно общим, чтобы через него мог проходить любой конус; с другой стороны, $L$ должно быть достаточно конкретным, чтобы для каждого конуса была возможна только одна такая факторизация.

можно охарактеризовать как конечные объекты в категории конусов F Пределы также .

Возможно, что диаграмма вообще не имеет предела. Однако если диаграмма имеет предел, то этот предел по существу единственен: он уникален с точностью до единственного изоморфизма . причине часто говорят о пределе F. По этой

Копределы

См. также: Прямой лимит

Двойственные понятия пределов и конусов — это копределы и коконусы. Хотя их определения легко получить путем обращения всех морфизмов в приведенных выше определениях, мы явно сформулируем их здесь:

Коконус ​ диаграммы $F:J\to C$ это объект $N$ из $C$ вместе с семейством морфизмов

$\psi _{X}:F(X)\to N$

для каждого объекта $X$ из $J$, такой, что для любого морфизма $f:X\to Y$ в $J$, у нас есть $\psi _{Y}\circ F(f)=\psi _{X}$.

Копредел ​ диаграммы $F:J\to C$ является коконусом $(L,\phi )$ из $F$ такой, что для любого другого коконуса $(N,\psi )$ из $F$ существует единственный морфизм $u:L\to N$ такой, что $u\circ \phi _{X}=\psi _{X}$ для всех $X$ в $J$.

A universal co-cone

Копределы также называют универсальными коконусами . Их можно охарактеризовать как исходные объекты в категории коконусов из $F$.

Как и в случае с пределами, если диаграмма $F$ имеет копредел, то этот копредел единственен с точностью до единственного изоморфизма.

Вариации

Пределы и копределы также можно определить для наборов объектов и морфизмов без использования диаграмм. Определения те же (обратите внимание, что в приведенных выше определениях нам никогда не требовалось использовать композицию морфизмов в $J$). Однако этот вариант не добавляет никакой новой информации. Любой набор объектов и морфизмов определяет (возможно, большой) ориентированный граф. $G$. Если мы позволим $J$ быть свободной категорией, созданной $G$, есть универсальная диаграмма $F:J\to C$ чье изображение содержит $G$. Предел (или копредел) этой диаграммы такой же, как предел (или копредел) исходного набора объектов и морфизмов.

Слабый предел и слабые копределы определяются так же, как пределы и копределы, за исключением того, что свойство уникальности опосредующего морфизма отбрасывается.

Примеры

Ограничения

Определение пределов является достаточно общим, чтобы включить в него несколько конструкций, полезных в практических условиях. Далее мы рассмотрим предел ( L , φ диаграммы F : J → C. )

• Терминальные объекты . Если J — пустая категория, существует только одна диаграмма формы J : пустая (аналогично пустой функции в теории множеств). по сути, просто объект C. Конус пустой диаграммы — это , Пределом F является любой объект, который однозначно учитывается всеми остальными объектами. Это всего лишь определение терминального объекта .
• Продукты . Если J — дискретная категория то диаграмма F , по сути, представляет собой не что иное, как семейство объектов C , индексированных J. , Предел L функции F называется произведением этих объектов. Конус φ состоит из семейства морфизмов φ _X : L → F ( X ), называемых проекциями произведения. в категории множеств Например, продукты представляют собой декартовы произведения , а проекции являются просто естественными проекциями на различные факторы.
  • Полномочия . Особый случай произведения — это когда диаграмма является постоянным функтором объекта X объекта C. F Предел этой диаграммы называется J ^й степень X X и обозначил ^Дж .
• Эквалайзеры . Если J — категория с двумя объектами и двумя параллельными морфизмами одного объекта в другой, то диаграмма формы J — это пара параллельных морфизмов C. в Предел L такой диаграммы называется эквалайзером этих морфизмов.
  • Ядра . Ядро нулевым — это частный случай эквалайзера, где один из морфизмов является морфизмом .
• Откаты . Пусть F — диаграмма, которая выбирает три объекта X , Y и Z в C единственными нетождественными морфизмами являются f : X → Z и g : Y → Z. , где Предел L функции F называется обратным ходом или расслоенным произведением . Его удобно представить в виде коммутативного квадрата :

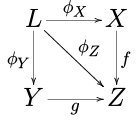
• Обратные пределы . Пусть J — направленное множество (рассматриваемое как малая категория путем добавления стрелок i → j тогда и только тогда, когда i ≥ j ), и пусть F : J ^на → C — диаграмма. Предел F называется обратным пределом или проективным пределом .
• Если J = 1 , категория с одним объектом и морфизмом, то диаграмма формы по сути является просто объектом X из C. J Конус объекта X — это просто морфизм с X. кодоменом Морфизм f : Y → X является пределом диаграммы X тогда и только тогда, когда f — изоморфизм . В более общем смысле, если J — любая категория с начальным объектом i , то любая диаграмма формы J имеет предел, а именно любой объект, изоморфный F ( i ). Такой изоморфизм однозначно определяет универсальный конус F .
• Топологические пределы . Пределы функций — это частный случай пределов фильтров , которые связаны с категориальными пределами следующим образом. Для топологического пространства X обозначим через F множество фильтров на X , x ∈ X — точка, V ( x ) — фильтр окрестности точки x , A — конкретный и фильтр $F_{x,A}=\{G\in F\mid V(x)\cup A\subset G\}$набор фильтров более тонких, чем A и сходящихся к x . Фильтрам F придается небольшая и тонкая структура категорий путем добавления стрелки A → B тогда и только тогда, когда A ⊆ B . Инъекция $I_{x,A}:F_{x,A}\to F$ становится функтором и имеет место следующая эквивалентность:

x является топологическим пределом A тогда и только тогда, когда A является категориальным пределом A. $I_{x,A}$

Копределы

Примеры копределов представлены двойными версиями приведенных выше примеров:

• Исходные объекты являются копределами пустых диаграмм.
• Копродукты — это копределы диаграмм, индексированных по дискретным категориям.
  • Костепени — это копределы постоянных диаграмм из дискретных категорий.
• Коэквалайзеры — это копределы параллельной пары морфизмов.
  • Коядра являются соэквалайзерами морфизма и параллельного нулевого морфизма.
• Pushouts — это копределы пары морфизмов с общей областью определения.
• Прямые пределы — это копределы диаграмм, индексированных направленными множествами.

Свойства

Наличие ограничений

Данная диаграмма F : J → C может иметь или не иметь предел (или копредел) в C . может вообще не существовать конуса Действительно, у F , не говоря уже об универсальном конусе.

категория C Говорят, что имеет пределы формы J если каждая диаграмма формы J имеет предел в C. , категория C В частности, говорят, что

• иметь продукты , если у него есть пределы формы J для каждой маленькой дискретной категории J (не обязательно иметь большие продукты),
• иметь эквалайзеры , если они имеют пределы формы $\bullet \rightrightarrows \bullet$ (т.е. каждая параллельная пара морфизмов имеет эквалайзер),
• иметь откаты , если у него есть пределы формы $\bullet \rightarrow \bullet \leftarrow \bullet$ (т.е. каждая пара морфизмов с общей кодоменой имеет обратный образ).

Полная категория — это категория, которая имеет все малые пределы (т.е. все пределы формы J для каждой малой категории J ).

Можно также дать двойственные определения. Категория имеет копредел формы J если каждая диаграмма формы J имеет копредел в C. , Кополная категория — это категория, которая имеет все малые копределы.

Теорема существования пределов что если категория C имеет эквалайзеры и все произведения индексированы классами Ob( J ) и Hom( J ), то C имеет все пределы формы J. утверждает , В этом случае предел диаграммы F : J → C можно построить как эквалайзер двух морфизмов

$s,t:\prod _{i\in \operatorname {Ob} (J)}F(i)\rightrightarrows \prod _{f\in \operatorname {Hom} (J)}F(\operatorname {cod} (f))$

задано (в компонентной форме)

${\begin{aligned}s&={\bigl (}F(f)\circ \pi _{\operatorname {dom} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}\\t&={\bigl (}\pi _{\operatorname {cod} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}.\end{aligned}}$

Существует двойственная теорема существования копределов в терминах коэквалайзеров и копроизведений. теоремы дают достаточные и необходимые условия существования всех (ко)пределов формы J. Обе эти

Универсальная собственность

Пределы и копределы — важные частные случаи универсальных конструкций .

Пусть C — категория, а J — категория малого индекса. Категория функтора C ^Дж можно рассматривать как категорию всех диаграмм J в C. формы Диагональный функтор

$\Delta :{\mathcal {C}}\to {\mathcal {C}}^{\mathcal {J}}$

— это функтор, который отображает каждый объект N в C в постоянный функтор Δ( N ) : J → C в N . То есть Δ( N )( X ) = N для каждого объекта X в J и Δ( N )( f ) = id _N для каждого морфизма f в J .

Дана диаграмма F : J → C (мыслимая как объект в C ^Дж ), естественное преобразование ψ : ∆( N ) → F (которое является всего лишь морфизмом в категории C ^Дж что конус от N до F. ) — это то же самое , Чтобы убедиться в этом, сначала заметим, что Δ( N )( X ) = N для всех X подразумевает, что компоненты ψ являются морфизмами ψ _X : N → F ( X ), которые все имеют общую область определения N . Более того, требование коммутации диаграмм конуса справедливо просто потому, что это ψ является естественным преобразованием. (Двойственным образом естественное преобразование ψ : F → Δ( N ) — это то же самое, что коконус из F в N .)

Следовательно, определения пределов и копределов можно затем переформулировать в виде:

• Предел F — это универсальный морфизм из ∆ в F .
• Копредел F — это универсальный морфизм из F в ∆.

Дополнения

Как и все универсальные конструкции, образование пределов и копределов носит функториальный характер. Другими словами, если каждая диаграмма формы J имеет предел в C (при малом J ), то существует предельный функтор

$\lim :{\mathcal {C}}^{\mathcal {J}}\to {\mathcal {C}}$

которое ставит в соответствие каждой диаграмме ее предел и каждому естественному преобразованию η : F → G единственный морфизм lim η : lim F → lim G , коммутирующий с соответствующими универсальными конусами. Этот функтор правосопряжён к диагональному функтору ∆ : C → C. ^Дж . Это дополнение дает биекцию между множеством всех морфизмов от N до lim F и множеством всех конусов от N до F.

$\operatorname {Hom} (N,\lim F)\cong \operatorname {Cone} (N,F)$

что естественно в переменных N и F . Единицей этого присоединения является просто универсальный конус от lim F до F . Если индексная категория J связна . (и непуста), то единица присоединения является изоморфизмом, так что lim — левая обратная к ∆ Это не удастся, если J не подключен. Например, если J — дискретная категория, компонентами единицы являются диагональные морфизмы δ : N → N. ^Дж .

Двойственно, если каждая диаграмма формы J имеет копредел в C (для J малого), существует копредельный функтор

$\operatorname {colim} :{\mathcal {C}}^{\mathcal {J}}\to {\mathcal {C}}$

который присваивает каждой диаграмме свой копредел. Этот функтор сопряжен слева с диагональным функтором ∆ : C → C. ^Дж , и существует естественный изоморфизм

$\operatorname {Hom} (\operatorname {colim} F,N)\cong \operatorname {Cocone} (F,N).$

Единицей этого присоединения является универсальный кокон от до colim F. F Если J связен (и непуст), то единица является изоморфизмом, так что colim является левым обратным числом ∆.

Обратите внимание, что как предельный, так и копредельный функторы являются ковариантными функторами.

функторов

См. Также: Предел и копредел предпучков.

Можно использовать функторы Hom, чтобы связать пределы и копределы в категории C с пределами в Set , категории множеств . Частично это следует из того факта, что ковариантный функтор Hom Hom( N , –) : C → Set сохраняет все пределы в C . В силу двойственности контравариантный функтор Hom должен доводить копределы до пределов.

Если диаграмма F : J → C имеет предел в C , обозначаемый lim F , существует канонический изоморфизм

$\operatorname {Hom} (N,\lim F)\cong \lim \operatorname {Hom} (N,F-)$

переменной N. что естественно по Здесь функтор Hom( N , F –) представляет собой композицию функтора Hom Hom( N , –) с F . Этот изоморфизм единственный, соблюдающий предельные конусы.

чтобы определить предел F в C. Можно использовать приведенное выше соотношение , Первый шаг — заметить, что предел функтора Hom( N , F –) можно отождествить с множеством всех конусов от N до F :

$\lim \operatorname {Hom} (N,F-)=\operatorname {Cone} (N,F).$

Предельный конус задается семейством отображений π _X : Cone( N , F ) → Hom( N , FX ), где π _X ( ψ ) = ψ _X . Если дан объект L из C вместе с естественным изоморфизмом Φ : Hom( L , –) → Cone(–, F ), объект L будет пределом F с предельным конусом, заданным Φ _L (id _L ). На причудливом языке это означает, что предел F является представлением функтора Cone(–, F ) : C → Set .

Двойственным образом, если диаграмма F : J → C имеет копредел в C , обозначаемый colim F , существует единственный канонический изоморфизм

$\operatorname {Hom} (\operatorname {colim} F,N)\cong \lim \operatorname {Hom} (F-,N)$

естественное по переменной N и учитывающее копредельные конусы. Отождествляя предел Hom( F –, N ) с множеством Cocone( F , N ), это соотношение можно использовать для определения копредела диаграммы F как представления функтора Cocone( F , –).

Обмен пределами и копределами множеств

Пусть I — конечная категория, а J — небольшая фильтрованная категория . Для любого бифунктора

$F:I\times J\to \mathbf {Set} ,$

существует естественный изоморфизм

$\operatorname {colim} \limits _{J}\lim _{I}F(i,j)\rightarrow \lim _{I}\operatorname {colim} \limits _{J}F(i,j).$

Другими словами, отфильтрованные копределы в Set коммутируют с конечными пределами. Также считается, что малые копределы коммутируют с малыми пределами.

Функторы и пределы

Если F : J → C — диаграмма в C и G : C → D — функтор то методом композиции (напомним, что диаграмма — это всего лишь функтор) получается диаграмма GF : J → D. , Тогда возникает естественный вопрос:

«Как пределы GF связаны с пределами F ?»

Сохранение ограничений

Функтор G : C → D индуцирует отображение из Cone( F ) в Cone( GF ): если Ψ — конус из N в F , то GΨ — конус из GN в GF . функтор G Говорят, что сохраняет пределы F если ( GL , Gφ ) является пределом GF , если ( L , φ ) является пределом F. , (Обратите внимание, что если предел F не существует, то G бессмысленно сохраняет пределы F .)

функтор G Говорят, что сохраняет все пределы формы J , если он сохраняет пределы всех диаграмм F : J → C . Например, можно сказать, что G сохраняет произведения, выравниватели, обратные преобразования и т. д. Непрерывный функтор — это тот, который сохраняет все малые пределы.

Аналогичные определения можно дать и для копределов. Например, функтор G сохраняет копределы F , если G ( L , φ ) является копределом GF когда ( L , φ ) является копределом F. , Конепрерывный функтор — это тот, который сохраняет все малые копределы.

Если C — полная категория , то по приведенной выше теореме существования пределов функтор G : C → D непрерывен тогда и только тогда, когда он сохраняет (малые) произведения и эквалайзеры. Дуально группа G конепрерывна тогда и только тогда, когда она сохраняет (малые) копроизведения и коэквалайзеры.

Важным свойством сопряженных функторов является то, что каждый сопряженный справа функтор непрерывен, а каждый сопряженный слева функтор конепрерывен. Поскольку сопряженных функторов существует множество, это дает многочисленные примеры непрерывных и конепрерывных функторов.

Для данной диаграммы F : J → C и функтора G : C → D , если и F , и GF имеют указанные пределы, существует единственный канонический морфизм.

$\tau _{F}:G\lim F\to \lim GF$

которое соблюдает соответствующие предельные конусы. Функтор G сохраняет пределы F тогда и только тогда, когда это отображение является изоморфизмом. Если категории C и D имеют все пределы формы J , то lim — функтор, а морфизмы τ _F образуют компоненты естественного преобразования

$\tau :G\lim \to \lim G^{J}.$

Функтор G сохраняет все пределы формы J тогда и только тогда, когда τ — естественный изоморфизм. , что функтор G В этом смысле можно сказать коммутирует с пределами ( с точностью до канонического естественного изоморфизма).

Сохранение пределов и копределов — это концепция, применимая только к ковариантным функторам. Для контравариантных функторов соответствующими понятиями будут функторы, переводящие копределы в пределы, или функторы, переводящие пределы в копределы.

Снятие ограничений

функтор G : C → D Говорят, что снимает пределы диаграммы F : J → C , если всякий раз, когда ( L , φ ) является пределом GF , существует предел ( L ′, φ ′) диаграммы F такой, что G ( L ′, φ ′) знак равно ( L , φ ). Функтор G снимает пределы формы J если он снимает пределы для всех диаграмм формы J. , Поэтому можно говорить о подъеме произведений, уравнителях, откатах и ​​т. д. Наконец, говорят, что G снимает ограничения , если оно снимает все ограничения. Существуют двойственные определения снятия копределов.

Функтор G однозначно снимает пределы для диаграммы F , если существует единственный конус прообраза ( L ′, φ ′) такой, что ( L ′, φ ′) является пределом F и G ( L ′, φ ′) = ( L , φ ). Можно показать, что G снимает ограничения однозначно тогда и только тогда, когда он снимает ограничения и является амнезиаком .

Снятие ограничений явно связано с сохранением ограничений. Если G снимает ограничения для диаграммы F и GF имеет предел, то F также имеет предел, и G сохраняет пределы F . Следует, что:

• Если G снимает ограничения всей формы J , а D имеет все пределы формы J , то C также имеет все пределы формы J , а G сохраняет эти пределы.
• Если G снимает все малые пределы и D полно, то C также полно и G непрерывно.

Двойственные утверждения для копределов одинаково верны.

Создание и отражение ограничений

Пусть F : J → C — диаграмма. функтор G : C → D Говорят, что

• создать пределы для F , если всякий раз, когда ( L , φ ) является пределом GF , существует единственный конус ( L ′, φ ′) в F такой, что G ( L ′, φ ′) = ( L , φ ), и, кроме того, этот конус является пределом F .
• отражать пределы для F , если каждый конус в F , образ которого под G является пределом GF, уже является пределом F .

Двойственно можно определить создание и отражение копределов.

Следующие утверждения, как легко видеть, эквивалентны:

• Функтор G создает пределы.
• Функтор G однозначно снимает ограничения и отражает ограничения.

Существуют примеры функторов, которые однозначно снимают пределы, но не создают и не отражают их.

Примеры

• Каждый представимый функтор C → Set сохраняет пределы (но не обязательно копределы). В частности, для любого объекта A из C это верно для ковариантного функтора Hom Hom( A ,–) : C → Set .
• Функтор забывания U : Grp → Set создает (и сохраняет) все малые пределы и отфильтрованные копределы ; однако U не сохраняет копродукции. Эта ситуация типична для алгебраических забывчивых функторов.
• F Свободный функтор : Set → Grp ( сопоставляющий каждому множеству S над свободную группу S ) сопряжен слева с забывчивым функтором U и, следовательно, конепрерывен. Это объясняет, почему свободное произведение двух свободных групп G и H является свободной группой, порожденной объединением генераторов G и H. дизъюнктным
• Функтор включения Ab → Grp создает пределы, но не сохраняет копроизведения (копроизведение двух абелевых групп является прямой суммой ).
• Забывчивый функтор Top → Set однозначно снимает пределы и копределы, но не создает ни того, ни другого.
• Пусть Met _c — категория метрических пространств с непрерывными функциями для морфизмов. Функтор забывчивости Met _c → Set снимает конечные пределы, но не снимает их однозначно.

Примечание по терминологии

В старой терминологии пределы назывались «обратными пределами» или «проективными пределами», а копределы - «прямыми пределами» или «индуктивными пределами». Это стало источником большой путаницы.

Есть несколько способов запомнить современную терминологию. Прежде всего,

• коядра,
• побочные продукты,
• коэквалайзеры и
• кодомены

являются типами копределов, тогда как

• ядра,
• продукты
• эквалайзеры и
• домены

это виды лимитов. Во-вторых, префикс «со» подразумевает «первую переменную $\operatorname {Hom}$«. Такие термины, как «когомология» и «корасслоение», имеют несколько более сильную связь с первой переменной, то есть контравариантной переменной, $\operatorname {Hom}$ бифунктор.

См. также

• Декартова замкнутая категория - Тип категории в теории категорий.
• Эквалайзер (математика) – набор аргументов, в которых две или более функции имеют одинаковое значение.
• Обратный предел - конструкция в теории категорий
• Продукт (теория категорий) - обобщенный объект в теории категорий.

Дальнейшее чтение

• Адамек, Иржи; Хорст Херрлих; Джордж Э. Шлитцер (1990). Абстрактные и конкретные категории (PDF) . Джон Уайли и сыновья. ISBN  0-471-60922-6 .
• Мак Лейн, Сондерс (1998). Категории для работающего математика . Тексты для аспирантов по математике . Том. 5 (2-е изд.). Спрингер-Верлаг . ISBN  0-387-98403-8 . Збл   0906.18001 .
• Борсо, Фрэнсис (1994). «Пределы». Справочник по категориальной алгебре . Энциклопедия математики и ее приложений 50-51, 53 [т.е. 52]. Том. 1. Издательство Кембриджского университета. ISBN  0-521-44178-1 .

Внешние ссылки

• Интерактивная веб-страница , генерирующая примеры пределов и копределов в категории конечных множеств. Автор Джоселин Пейн .
• Лимит в n Lab