Так же, как эксперимент с ластиком
| Часть серии статей о |
| Квантовая механика |
|---|
В квантовой механике эксперимент с квантовым ластиком представляет собой эксперимент с интерферометром , который демонстрирует несколько фундаментальных аспектов квантовой механики , включая квантовую запутанность и дополнительность . [ 1 ] [ 2 ] : 328 Эксперимент с квантовым ластиком — это вариация эксперимента Томаса Янга классического с двумя щелями . Он устанавливает, что когда предпринимаются действия по определению, через какую из двух щелей прошел фотон, фотон не может интерферировать сам с собой. При такой маркировке потока фотонов не будут видны интерференционные полосы, характерные для эксперимента Юнга. Эксперимент также создает ситуации, в которых фотон, который был «помечен», чтобы показать, через какую щель он прошел, позже может быть «не помечен». Фотон, который был «немаркирован», снова будет интерферировать сам с собой, восстанавливая полосы, характерные для эксперимента Янга. [ 3 ]
История
[ редактировать ]Эксперимент с квантовым ластиком был предложен в 1982 году Марланом Скалли и Каем Дрюлем в статье « Квантовый ластик: предлагаемый эксперимент по корреляции фотонов, касающийся наблюдения и «отложенного выбора» в квантовой механике , как реализуемый способ проверить до сих пор непроверенные предсказания квантовой механики. В качестве вдохновения в статье упоминаются Юджина Вигнера сосредоточенность на проблеме измерения , беседы с Уиллисом Лэмбом и мысленные эксперименты Джона Арчибальда Уиллера . В документе также указывается, что эксперимент можно провести в режиме отложенного выбора , как это было задумано в мысленных экспериментах Уиллера, что теперь известно как квантовый ластик с отложенным выбором . [ 4 ]
Эксперимент
[ редактировать ]Концепция
[ редактировать ]В этом эксперименте используется аппарат с двумя основными секциями. После создания двух запутанных фотонов каждый направляется в свою секцию аппарата. Все, что делается для того, чтобы узнать путь запутанного партнера исследуемого фотона в двухщелевой части аппарата, будет влиять на второй фотон, и наоборот. Преимущество манипулирования запутанными партнерами фотонов в двухщелевой части экспериментальной установки состоит в том, что экспериментаторы могут разрушать или восстанавливать интерференционную картину в последней, ничего не меняя в этой части установки. Экспериментаторы делают это, манипулируя запутанным фотоном, и они могут делать это до или после того, как его партнер пройдет через щели и другие элементы экспериментальной установки между излучателем фотонов и экраном обнаружения. В условиях, когда часть эксперимента с двумя щелями была организована для предотвращения появления интерференционных явлений (поскольку присутствует точная информация о том, какой путь), квантовый ластик можно использовать для эффективного стирания этой информации. При этом экспериментатор восстанавливает интерференцию, не изменяя двухщелевую часть экспериментальной установки. [ 3 ]
Вариант этого эксперимента, квантовый ластик с отложенным выбором , позволяет отложить принятие решения о том, измерять или уничтожить информацию о «каком пути», до тех пор, пока запутанная частица-партнер (тот, кто проходит через щели) либо не вмешается сама в себя, либо нет. . [ 5 ] В экспериментах с отложенным выбором квантовые эффекты могут имитировать влияние будущих действий на прошлые события. [ 6 ] Однако временной порядок измерительных действий не имеет значения. [ 7 ]
Процедура
[ редактировать ]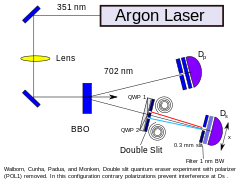
Сначала фотон пропускается через специализированное нелинейное оптическое устройство : кристалл бета-бората бария (BBO). [ 3 ] Этот кристалл преобразует одиночный фотон в два запутанных фотона более низкой частоты — процесс, известный как спонтанное параметрическое преобразование с понижением частоты (SPDC). Эти запутанные фотоны следуют разными путями. Один фотон попадает непосредственно в поляризационно-разрешающий детектор, а второй фотон проходит через двухщелевую маску ко второму поляризационно-разрешающему детектору. Оба детектора подключены к схеме совпадений , обеспечивающей подсчет только запутанных пар фотонов. Шаговый двигатель перемещает второй детектор для сканирования целевой области, создавая карту интенсивности. Эта конфигурация дает знакомую интерференционную картину.
Затем круговой поляризатор перед каждой щелью двухщелевой маски помещается , который создает круговую поляризацию по часовой стрелке для света, проходящего через одну щель, и круговую поляризацию против часовой стрелки в другую щель (см. рисунок 1). (Какая щель соответствует какой поляризации, зависит от поляризации, сообщаемой первым детектором.) Эта поляризация измеряется на втором детекторе, таким образом «маркируя» фотоны и разрушая интерференционную картину (см. Законы Френеля – Араго ).
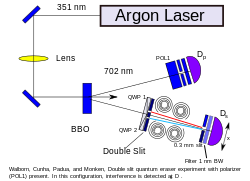
Наконец, линейный поляризатор на пути первого фотона запутанной пары вводится , придающий этому фотону диагональную поляризацию (см. рисунок 2). Запутывание обеспечивает дополнительную диагональную поляризацию партнера, проходящего через двухщелевую маску. Это изменяет эффект круговых поляризаторов: каждый из них будет производить смесь света, поляризованного по часовой стрелке и против часовой стрелки. Таким образом, второй детектор больше не может определить, какой путь был выбран, и интерференционные полосы восстанавливаются.
Двойную щель с вращающимися поляризаторами также можно объяснить, рассматривая свет как классическую волну. [ 8 ] Однако в этом эксперименте используются запутанные фотоны, которые несовместимы с классической механикой.
Другие приложения
[ редактировать ]Технологию квантового стирания можно использовать для увеличения разрешения современных микроскопов . [ 9 ]
Распространенное заблуждение
[ редактировать ]Распространенное заблуждение относительно этого эксперимента заключается в том, что его можно использовать для мгновенной передачи информации между двумя детекторами. [ 10 ] Однако простая причинно-следственная связь не позволяет навязывать «данную» информацию о наблюдаемых результатах. Важно понять роль детектора совпадений в этой экспериментальной установке. Линейный поляризатор на верхнем пути эффективно отфильтровывает половину запутанных фотонов, а через детектор совпадений отфильтровывает соответствующие фотоны на нижнем пути. Детектор совпадений может работать только путем сравнения данных с обоих датчиков, что делает невозможным использование этой установки для мгновенной связи.
Другими словами, лишь небольшой процент света, проходящего через кристалл BBO, расщепляется на запутанные пары. Подавляющее большинство фотонов, проходящих через кристалл, не расщепляются и должны быть удалены из окончательного набора данных как нежелательный шум. Поскольку у детекторов нет возможности измерить, был ли фотон частью запутанной пары, это решение принимается путем анализа времени и фильтрации любых фотонов, которые не были пойманы в то же время, что и их фотоны. двойник на другом детекторе. Таким образом, когда создается пара запутанных фотонов, но один из двух блокируется поляризатором и теряется, оставшийся фотон будет отфильтрован из набора данных, как если бы он был одним из многих незапутанных фотонов. С этой точки зрения неудивительно, что внесение изменений в верхний путь может повлиять на измерения, проводимые на нижнем пути, поскольку два измерения сравниваются и используются для фильтрации данных.
Обратите внимание, что в конечном состоянии этой экспериментальной установки измерения на нижнем пути всегда показывают размытую картину необработанных данных. Увидеть интерференционную картину можно только фильтруя данные детектором совпадений и рассматривая только фотоны, составляющие 1/2 запутанной пары.
Ссылки
[ редактировать ]- ^ Энглерт, Бертольд-Георг (1999). «Замечания по некоторым основным вопросам квантовой механики» (PDF) . Журнал естественных исследований . 54 (1): 11–32. Стартовый код : 1999ЗНатА..54...11Е . дои : 10.1515/zna-1999-0104 . S2CID 3514379 . Архивировано из оригинала (PDF) 9 августа 2017 г. Проверено 10 апреля 2019 г.
- ^ Бэгготт, Дж. Э. (2013). Квантовая история: история за 40 мгновений (Впечатление: 3-е изд.). Оксфорд: Оксфордский университет. Нажимать. ISBN 978-0-19-965597-7 .
- ^ Jump up to: а б с Уолборн, СП; Терра Кунья, Миссури; Падуя, С.; Монкен, Швейцария (20 февраля 2002 г.). «Квантовый ластик с двумя щелями» . Физический обзор А. 65 (3): 033818. arXiv : quant-ph/0106078 . Бибкод : 2002PhRvA..65c3818W . дои : 10.1103/PhysRevA.65.033818 . ISSN 1050-2947 .
- ^ Скалли, Мэриан О.; Дрюль, Кай (1982). «Квантовый ластик: предлагаемый эксперимент по корреляции фотонов, касающийся наблюдения и «отложенного выбора» в квантовой механике». Физический обзор А. 25 (4): 2208–2213. Бибкод : 1982PhRvA..25.2208S . дои : 10.1103/PhysRevA.25.2208 .
- ^ Юн-Хо, Ким; Ю, Р.; Кулик, ИП; Ши, Ю.Х.; Скалли, Марлан (2000). «Квантовый ластик отложенного выбора». Письма о физических отзывах . 84 (1): 1–5. arXiv : Quant-ph/9903047 . Бибкод : 2000PhRvL..84....1K . doi : 10.1103/PhysRevLett.84.1 . ПМИД 11015820 . S2CID 5099293 .
- ^ Фанкхаузер, Йоханнес (2019). «Укрощение квантового ластика отложенного выбора». Кванта . 8 : 44–56. arXiv : 1707.07884 . дои : 10.12743/quanta.v8i1.88 . S2CID 53574007 .
- ^ Ма, Сяо-сун; Кофлер, Йоханнес; Цайлингер, Антон (2016). «Мысленные эксперименты с отложенным выбором и их реализации». Преподобный Мод. Физ . 88 (1): 015005. arXiv : 1407.2930 . Бибкод : 2016РвМП...88а5005М . дои : 10.1103/RevModPhys.88.015005 . S2CID 34901303 .
- ^ Цзяо, Республика Корея; Квиа, П.Г.; Стейнберг, AM (июнь 1995 г.). «Квантовая нелокальность в двухфотонных экспериментах в Беркли». Квантовая и полуклассическая оптика: Журнал Европейского оптического общества, часть B. 7 (3): 259–278. arXiv : Quant-ph/9501016 . Бибкод : 1995QuSOp...7..259C . дои : 10.1088/1355-5111/7/3/006 . S2CID 118987962 .
- ^ Ааронов, Якир; Зубайри, М. Сухайль (2005). «Время и квант: стирание прошлого и влияние на будущее». Наука . 307 (5711): 875–879. Бибкод : 2005Sci...307..875A . CiteSeerX 10.1.1.110.2955 . дои : 10.1126/science.1107787 . PMID 15705840 . S2CID 16606155 .
- ^ Кастнер, Р.Э. (01 июля 2019 г.). «Квантовый ластик с отложенным выбором» не стирает и не задерживает» . Основы физики . 49 (7): 717–727. arXiv : 1905.03137 . Бибкод : 2019FoPh...49..717K . дои : 10.1007/s10701-019-00278-8 . ISSN 0015-9018 . Кастнер (2019): «Квантовый ластик с отложенным выбором не стирает и не задерживает», «Основы физики».
