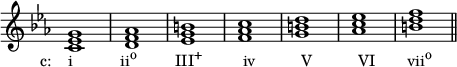Анализ римских цифр

В музыки теории анализ римских цифр — это тип гармонического анализа , в котором аккорды представлены римскими цифрами аккорда , которые кодируют степень и гармоническую функцию в пределах данной музыкальной тональности .
Конкретные соглашения об обозначениях различаются: некоторые теоретики используют цифры в верхнем регистре (например, I, IV, V) для обозначения мажорных аккордов и цифры в нижнем регистре (например, ii, iii, vi) для обозначения второстепенных аккордов . Другие используют цифры в верхнем регистре для всех аккордов, независимо от их качества . [2]
Римские цифры можно использовать для обозначения и анализа гармонического развития композиции независимо от ее конкретной тональности . Например, вездесущая двенадцатитактовая блюзовая прогрессия использует тонику (I), субдоминанту IV и доминанту (V) аккорды, построенные на первой, четвертой и пятой ступенях гаммы соответственно.
История
[ редактировать ]
Анализ римских цифр основан на идее, что аккорды могут быть представлены и названы по одной из их нот, их корню ( История основного тона (аккорда)» дополнительную информацию см. в статье « ). Система возникла изначально на основе работ и сочинений Рамо басиста фундаментального .
Самое раннее использование римских цифр можно найти в первом томе книги Иоганна Кирнбергера « Искусство чистого предложения» 1774 года. [3] Вскоре после этого аббат Георг Йозеф Фоглер время от времени использовал римские цифры при основании Kuhrpfälzische Tonschule в 1778 году. [4] Он также упомянул их в своем Handbuch zur Harmonielehre 1802 года и использовал анализ римских цифр в нескольких публикациях, начиная с 1806 года. [5]
Готфрида Вебера Versuch einer geordneten Theorie der Tonsetzkunst ( Теория музыкальной композиции Популяризацию этого метода часто приписывают книге ) (1817–1821). Точнее, он ввел использование больших заглавных цифр для мажорных аккордов, маленьких заглавных для второстепенных, надстрочного индекса. тот для уменьшенных пятых и пунктирных 7 для больших седьмых – см. рисунок ниже. [6] Симон Зехтер, считающийся основателем венской « Теории степеней » ( Stufentheorie ), лишь ограниченно использовал римские цифры, всегда в виде заглавных букв, и часто отмечал основные положения буквенными обозначениями или арабскими цифрами. [7] Антон Брукнер , передавший теорию Шенбергу и Шенкеру , по-видимому, не использовал римские цифры на своих занятиях в Вене. [8]
Цифры общей практики
[ редактировать ]В теории музыки, связанной с периодом общепринятой практики или полученной из нее , римские цифры часто используются для обозначения ступеней гаммы , а также построенных на них аккордов. [2] Однако в некоторых контекстах арабские цифры с каретками используются для обозначения самих ступеней шкалы (например, ![]() ,
, ![]() ,
, ![]() , ...).
, ...).
Основные символы анализа римских цифр, обычно используемые в педагогических текстах, показаны в таблице ниже. [9] [10] : 71
Символ Значение Примеры Римская цифра в верхнем регистре Мажорная триада я Строчная римская цифра Минорное трезвучие я Надстрочный индекс + Дополненная триада я + Надстрочный индекс тот Уменьшенная триада я тот Надстрочный номер Добавлено примечание V 7 Два и более числа( #-# ) Фигурная басовая нотация V 4–3 Надстрочный индекс # и #
#Первая инверсия я 6 Вторая инверсия я 6
4
Ниже показаны римские цифры семи диатонических трезвучий в корневых позициях, построенных на нотах гаммы до мажор.
Кроме того, согласно «Музыке: в теории и практике» , «иногда необходимо указать диез, бемоль или естественные ноты над басовой нотой». [10] : 74 Случайные символы могут располагаться под номерами верхнего и нижнего индекса, перед номером(ами) верхнего и нижнего индекса или с использованием косой черты (/) или знака плюса (+), чтобы указать, что интервал увеличен (либо ♮ в плоской форме). ключевая подпись или ♯ или ![]() в резкой ключевой подписи.
в резкой ключевой подписи.
Второстепенные аккорды обозначаются косой чертой, например V/V.
Современные шенкерианцы часто предпочитают использовать большие заглавные числа для всех степеней во всех формах, в соответствии с собственным использованием Шенкера. [а]

Инверсии
[ редактировать ]
Римские цифры иногда дополняются арабскими цифрами для обозначения обращения аккордов. Система аналогична системе фигурного баса : арабские цифры обозначают характерный интервал(ы) над басовой нотой аккорда, цифры 3 и 5 обычно опускаются. Первая инверсия обозначается цифрой 6 (например, I 6 для первого обращения тонического трезвучия, хотя для полного расчета мне потребовалось бы 6
3 ); цифры 6
4 обозначает вторую инверсию (например, I 6
4 ). Перевернутые септаккорды аналогично обозначаются одной или двумя арабскими цифрами, описывающими наиболее характерные интервалы, а именно интервал секунды между септаккордом и основным тоном: V 7 является доминирующей седьмой ступенью (например, G–B–D–F); В 6
5 – его первая инверсия (Б–Г– Ж–Г ); В 4
3 — его вторая инверсия (D– F–G –B); и В. 4
2 или В 2 его третья инверсия ( F–G –B–D). [10] : 79–80
В Соединенном Королевстве существует еще одна система, в которой римские цифры сочетаются с латинскими буквами для обозначения инверсии. [13] В этой системе суффикс «a» используется для обозначения корневой позиции, «b» для первой инверсии и «c» для второй инверсии. Однако «а» редко используется для обозначения корневой позиции, так же, как и 5
3 редко используется для обозначения корневой позиции в американской номенклатуре. [14] [ не удалось пройти проверку – см. обсуждение ] [15] [16] [17]
Джазовые и поп-цифры
[ редактировать ]
В теории музыки, фальшивых книгах и ведущих листах, ориентированных на джаз и популярную музыку , многие мелодии и песни написаны в тональности, и поэтому для всех аккордов даются названия букв и символы для всех трезвучий (например, C, G). 7 , Дм и др.). В некоторых поддельных книгах и свинцовых листах все трезвучия могут быть представлены цифрами в верхнем регистре, за которыми следует символ, указывающий, не является ли это мажорным аккордом (например, «m» для минора или «m»). ø " для полууменьшенного или "7" для септаккорда). Под мажорным аккордом понимается цифра в верхнем регистре, за которой не следует символ. Использование римских цифр позволяет исполнителям ритм-секции играть песню в любой тональности. по запросу руководителя оркестра или солиста . Исполнители аккомпанемента переводят римские цифры в конкретные аккорды, которые будут использоваться в данной тональности.
В тональности ми мажор диатонические аккорды:
- И май7 становится я май7 (также я ∆7 , или просто я)
- F ♯ m 7 становится II м7 (также II −7 , II мин7 , IIm или II − )
- G ♯ m 7 становится III м7 (также III −7 , III мин7 , IIIm или III − )
- А май7 становится IV май7 (также IV ∆7 , или просто IV)
- Б 7 становится V 7 (или просто V; часто V 9 или В 13 в контексте джаза)
- C ♯ m 7 становится VI м7 (т.е. VI −7 , ВИ мин7 , VIm или VI − )
- D ♯ ø7 становится VII ø7 (также VII m7b5 , VII -7b5 , или VII ø )
В популярной музыке и рок-музыке обычно происходит «заимствование» аккордов из параллельного минора мажорной тональности. Таким образом, в этих жанрах в тональности ми мажор такие аккорды, как ре мажор (или ♭ VII), соль мажор ( ♭ III) и до мажор ( ♭ обычно используются VI). Все эти аккорды заимствованы из тональности ми минор. Точно так же в минорных тональностях могут быть «заимствованы» аккорды параллельного мажора. Например, в ми миноре диатонический аккорд, построенный на четвертой ступени гаммы, — IVm, или ля минор. Однако на практике во многих песнях ми минор используется IV (ля мажор), заимствованный из тональности ми мажор. Однако заимствование из параллельного мажора в минорной тональности встречается гораздо реже.
Использование аккорда V7 или V (V доминантная 7 или V мажор) типично для большинства джазовой и поп-музыки, независимо от того, является ли тональность мажорной или минорной. Хотя аккорд V не является диатоническим в минорной гамме, его использование в минорной тональности обычно не считается «заимствованием», учитывая его распространенность в этих стилях.
Диатонические гаммы
[ редактировать ]Мажорный масштаб
[ редактировать ]В таблице ниже показаны римские цифры для аккордов, построенных в мажорной гамме .
Степень шкалы Тоник Супертоник через Субдоминант Доминантный Посредничество Ведущий тон Обычные обозначения я ii III IV V мы VII тот Альтернативные обозначения я II III IV V МЫ VII [18] Символ аккорда В мае II мин. III мин. IV мая В Маж (или В 7 ) VI мин. VII тусклый (или VII тот )
В тональности до мажор эти аккорды
Минорный масштаб
[ редактировать ]В таблице ниже приведены римские цифры для аккордов, построенных по гамме натурального минора .
Степень шкалы Тоник Супертоник через Субдоминант Доминантный Посредничество Субтонический Ведущий тон Обычные обозначения я ii тот ♭ III iv v ♭ VI ♭ VII VII тот Альтернативные обозначения я ii III iv v мы VII Символ аккорда Через мин. II тусклый ♭ III августа
(или III майор)IV мин
(или IV майор)V min
(или В. 7 )♭ VI май ♭ VII май VII Солнце
(или VII тот )
В тональности до минор (натуральный минор) эти аккорды звучат так:
Седьмая ступень гаммы очень часто повышается на полтона, чтобы сформировать ведущий тон, делая доминантный аккорд (V) мажорным аккордом (т.е. V мажор вместо v минор), а субтонический аккорд (vii) — уменьшенным аккордом (vii тот , вместо ♭ VII). Эта версия минорной гаммы называется гармонической минорной гаммой . Это позволяет композиторам иметь доминантный аккорд (V), а также доминирующий септаккорд (V7), оба доступны для более сильного разрешения каденции в минорной тональности, то есть от V до i минора.
Режимы
[ редактировать ]В традиционных обозначениях триады семи современных ладов следующие:
Нет. Режим Тоник Супертоник через Субдоминант Доминантный Посредничество Субтонический /
Ведущий тон1 Ионический (основной) я ii III IV V мы VII тот 2 Дориан я ii ♭ III IV v мы тот ♭ VII 3 фригийский я ♭ II ♭ III iv v тот ♭ VI ♭ vii 4 лидийский я II III ♯ iv тот V мы VII 5 миксолидийский я ii III тот IV v мы ♭ VII 6 Эолийский (натуральный минор) я ii тот ♭ III iv v ♭ VI ♭ VII 7 локрийский я тот ♭ II ♭ iii iv ♭ V ♭ VI ♭ vii
Сноски
[ редактировать ]- ^ Как символ Stufe , римская цифра «I» до мажор может обозначать мажорный аккорд, минорный аккорд, септаккорд или даже множество комбинаций нот, контролируемых корнем C. Та же самая римская цифра может также обозначать определяющая гармоническая функция расширенного отрывка, охватывающего несколько или множество аккордов. Поэтому в этой системе ко всем проявлениям структурной гармонии применяется один основной знак, с фигурно-басовыми цифрами и другими символами, обозначающими инверсии и отклонения от основного типа. ... Римские цифры можно использовать не столько для обозначения местных деталей, сколько в более широком и аналитическом смысле для обозначения гармонической функции как в мажорном, так и в второстепенном ладе. Этот метод предполагает свободное знание качества аккордов в обоих режимах — навык, который мы считаем столь же фундаментальным, как и распознавание тональностей . [11]
Ссылки
[ редактировать ]- ^ Уильям Дж. Эндрюс и Молли Склейтер (2000). Материалы западной музыки. Часть 1 , с. 227. ISBN 1-55122-034-2 .
- ^ Jump up to: а б Роджер Сешнс (1951). Гармоничная практика . Нью-Йорк: Харкорт, Брейс. LCCN 51-8476 . п. 7.
- ^ Иоганн Филипп Кирнбергер , Искусство чистого предложения , том. I. Берлин и Кенигсберг, Декер и Гартунг, 1774, с. 15 и таблички к стр. 19. Однако не совсем ясно, обозначают ли римские цифры в Кирнбергере степени шкалы или интервалы (или и то, и другое).
- ^ Дэвид Дамшредер, Размышляя о гармонии: исторические перспективы анализа . ISBN 978-0-521-88814-1 . Издательство Кембриджского университета, 2008, с. 6
- ^ Флойд К. Грейв и Маргарет Г. Грейв, Во славу гармонии: учение аббата Георга Йозефа Фоглера . [ нужна полная цитата ]
- ^ Готфрид Вебер, Попытка упорядоченной теории искусства музыкальной композиции , 3-е издание, Майнц, Шотт, 1830–1832, том. 2, стр. 44–63, §§ 151–158.
- ^ Саймон Зехтер, Правильная последовательность основных гармоний , Лейпциг, Брейткопф и Хертель, 3 тома, 1853–1854. Римские цифры встречаются во всех трех томах.
- ^ Антон Брукнер , Лекции по гармонии и контрапункту в Венском университете , изд. Э. Шванзара, Вена, Östrereichischer Bundesverlag, 1950. См. также Роберт Э. Уэйсон, Венская гармоническая теория от Альбрехтсбергера до Шенкера и Шенберга , Анн-Арбор, UMI Research Пресс, 1982. ISBN 0-8357-1586-8 . стр. 67–84.
- ^ Эрик Тейлор (1989). Руководство AB по теории музыки . Том. Часть 1. Лондон: Ассоциированный совет Королевских музыкальных школ. стр. 60–61. ISBN 1-85472-446-0 .
- ^ Jump up to: а б с Брюс Бенвард; Мэрилин Надин Сейкер (2003). Музыка: в теории и практике . Том. Я (седьмое изд.). Бостон: МакГроу-Хилл. ISBN 978-0-07-294262-0 .
- ^ Эдвард Олдуэлл; Карл Шахтер; Аллен Кадуолладер (2011). Гармония и голосовое лидерство (4-е изд.). Ширмер, Cengage Learning. стр. 696–697. ISBN 978-0-495-18975-6 .
- ^ Генрих Шенкер , Harmonielehre , Штутгарт, Берлин, Котта, 1906, с. 186, Пример 151.
- ^ Лавлок, Уильям (1981). Рудименты музыки . Лондон: Белл и Хайман. ISBN 0-7135-0744-6 .
- ^ «musictheory.net» . www.musictheory.net . Проверено 29 ноября 2020 г.
- ^ Бен (2 декабря 2013 г.). «Обращение аккордов» . Академия теории музыки . Проверено 6 декабря 2020 г.
- ^ Робсон, Элси Мэй (1960-е). Гармония, мелодическая изобретательность, инструменты оркестра, форма в музыке . Сидней: Николсон.
- ^ Спирритт, Гордон (1995). Основная теория музыки . Мельбурн: Алланс Образовательный.
- ^ Джон Мехеган (1989). Тональные и ритмические принципы . Джазовая импровизация. Том. 1 (Пересмотренное и дополненное изд.). Нью-Йорк: Уотсон-Гуптилл. стр. 9–16. ISBN 0-8230-2559-4 .